Лекции - В.Л.Пантелеев Курс лекций Теория фигуры Земли
Подождите немного. Документ загружается.


(3.16)
Существует и другой класс шаровых функций, который приведем здесь без вывода
(3.17)
где
-- та же сферическая функция, которая входит и в формулу (3.16).
Число постоянных шаровой функции степени
равно . Убедимся в этом на
при мере шаровой функции третьей степени:
Всего однородный полином третьей степени имеет 10 постоянных. Однако не все
постоянные независимы. Шаровые функции подчиняются уравнению Лапласа.
Выполнив необходимые выкладки, получим
Следовательно, из 10 постоянных 3 линейно связаны уравнением Лапласа. Остается
10-3=7 независимых постоянных.
3.3.1 Дифференциальное уравнение для сферических
функций
Поскольку шаровые функции удовлетворяют уравнению Лапласа, то есть
то должны выполняться и уравнения
В последнем варианте шаровые функции записаны в сферических координатах, поэтому нам
необходимо уравнение Лапласа переписать также в сферических координатах.
Из дифференциальной геометрии известно, что если
, , -- обобщенные
координаты, то элемент дуги в этой системе координат будет иметь вид
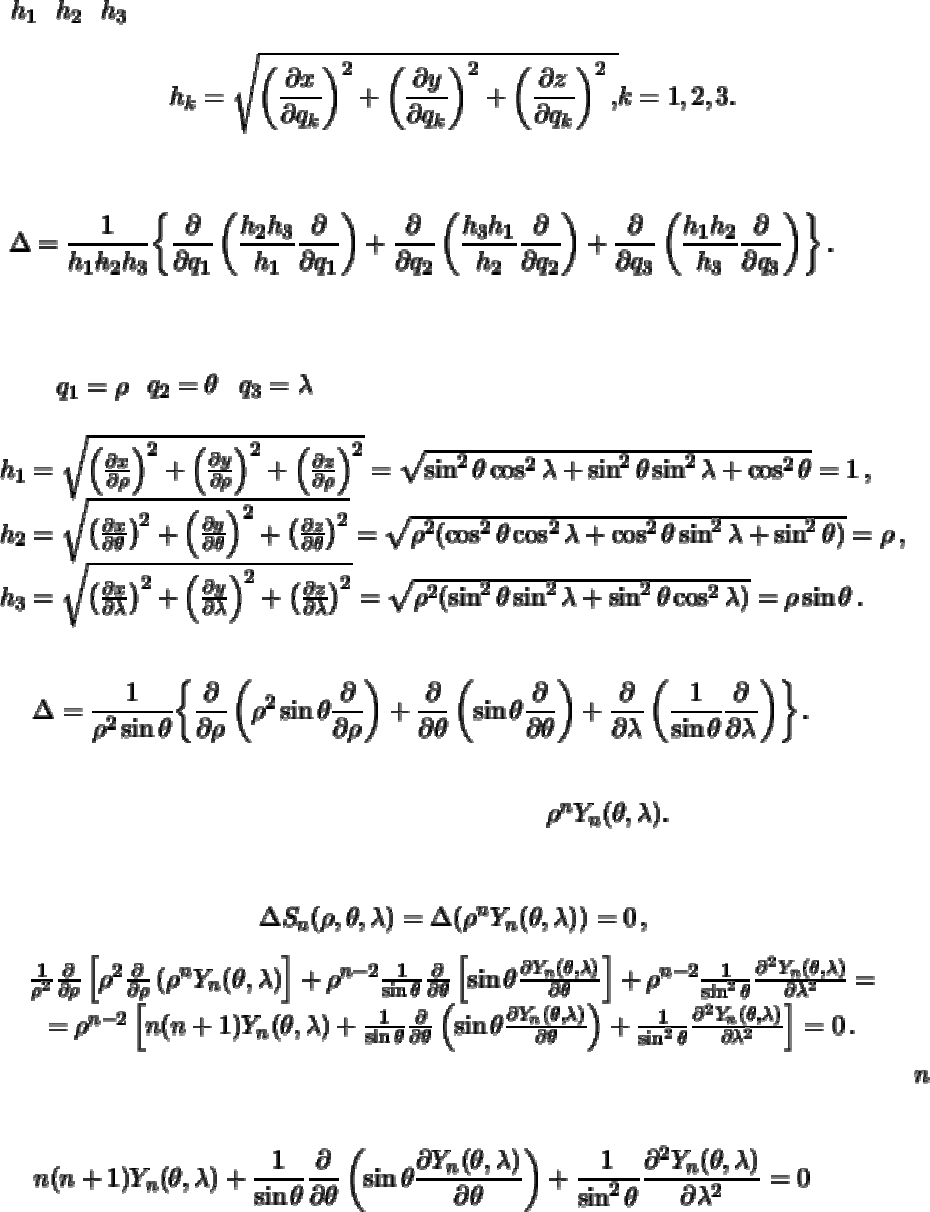
где , , -- коэффициенты Ламе:
Теперь оператор Лапласа можно определить следующим образом (без вывода)
(3.18)
Определим коэффициенты Ламе для сферической системы координат. В данном
случае , , , поэтому
Оператор Лапласа для сферических координат будет выглядеть так
(3.19)
Применим этот оператор к шаровой функции вида
Очевидно, что
оператор Лапласа для шаровой функции равен нулю, поэтому
Таким образом, дифференциальное уравнение для сферической функции порядка
имеет вид
(3.20)
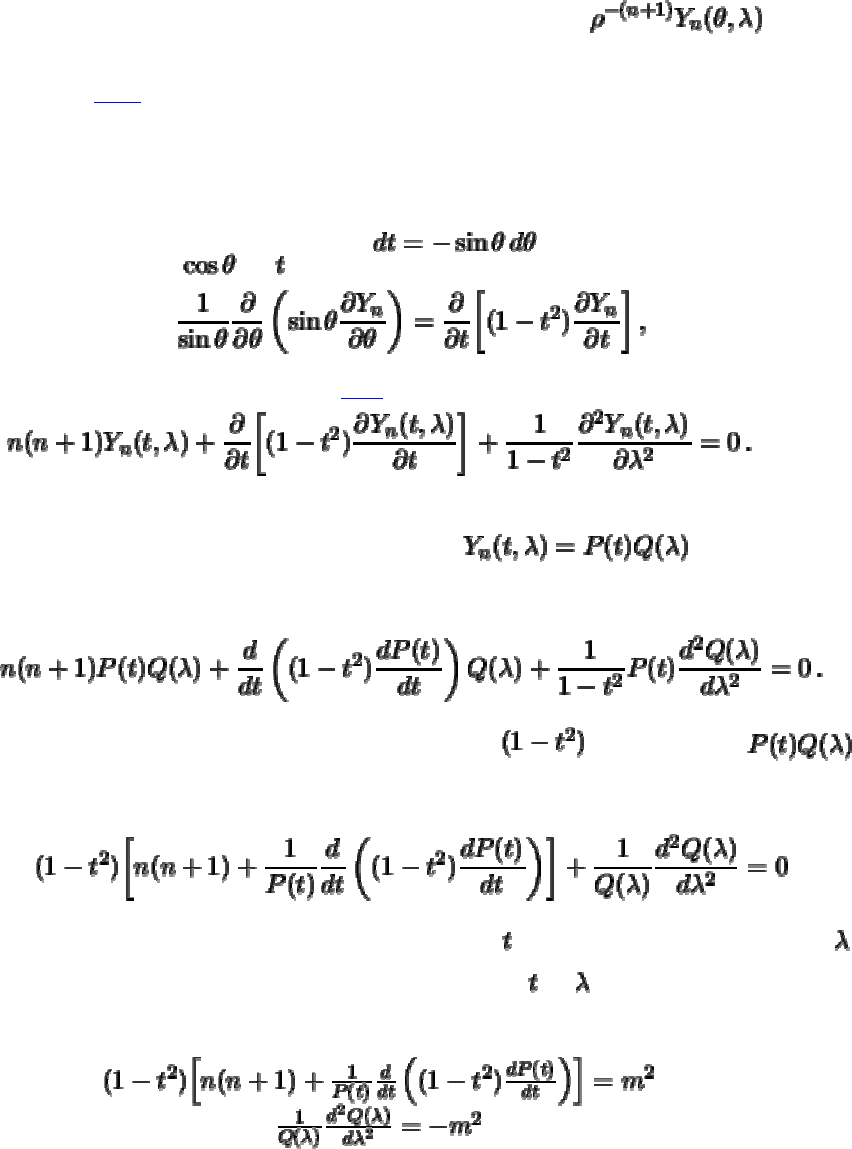
Предлагаем самостоятельно убедиться в том, что дифференциальное уравнение
для функции входящую в шаровую функцию второго рода
совпадает
с уравнением (
3.20).
3.3.2 Интегрирование дифференциального уравнения
Заменим переменную на . тогда . Очевидно, что
поэтому дифференциальное уравнение (3.20) можно переписать так
(3.21)
Будем искать решение этого уравнения в виде
. Подставив это
выражение в дифференциальное уравнение, будем иметь
Умножив каждый член полученного выражения на
и поделив на ,
получим
Видим, что первые два члена зависят только от
, а последний -- только от Для
того, чтобы уравнение выполнялось для любых
и , необходимо, чтобы эти
функции выродились в константы. Например, уравнение будет выполняться, если
(3.22)
Второе уравнение есть уравнение гармонических колебаний
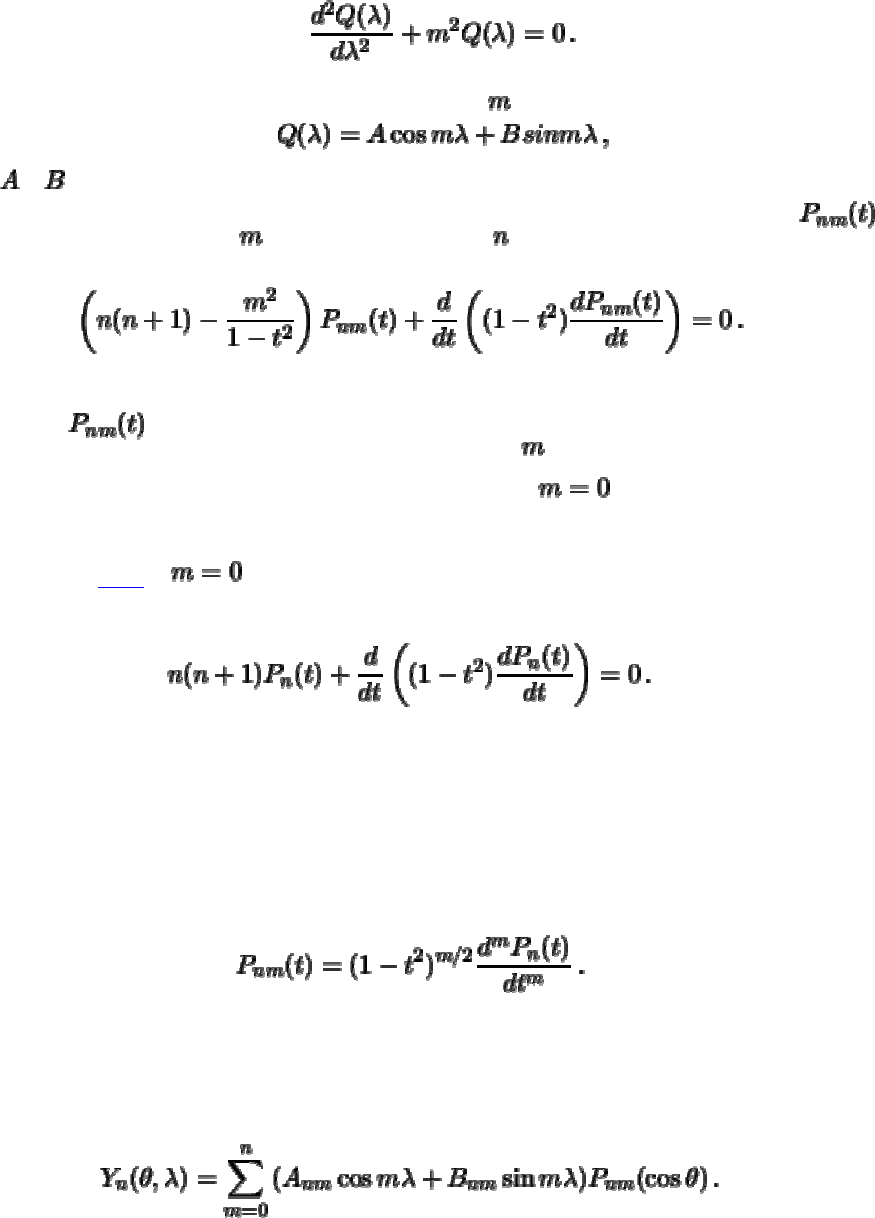
Его решение для любых действительных значений
имеет вид
где
и -- постоянные интегрирования. Решение первого из приведенных выше уравнений,
зависит как от постоянной , так и от постоянной . Обозначив решение через ,
получим
(3.23)
Функция
при целочисленных значениях носит название
присоединенной
(ассоциативной) функции Лежандра.
В случае , эти функции становятся
степенными полиномами, которые называются
полиномами Лежандра.
Полагая в
уравнении (
3.23) , получим дифференциальное уравнение для полиномов
Лежандра
(3.24)
В теории специальных функций свойства функций и полиномов Лежандра
достаточно хорошо изучены. Приведем лишь некоторые сведения (без вывода),
которые могут пригодиться в нашем курсе. Присоединенные функции Лежандра и
полиномы Лежандра связаны между собой соотношением
(3.25)
Подводя итог сказанному, выпишем окончательный вид решения
дифференциального уравнения для сферических функций
(3.26)

Заметим, что
порядок
производной в (3.25) не может быть больше
степени
полинома Лежандра. По этой причине постоянные и называют степенью и
порядком сферических функций.
Лекция 4. Сферические функции
• 4.1 Полиномы Лежандра и их свойства
• 4.2 Нормированные сферические функции
• 4.3 Аналитическое представление функции, заданной на поверхности сферы, рядом
Лапласа
4.1 Полиномы Лежандра и их свойства
Как мы видели, для вычисления сферических функций необходимо пользоваться
полиномами и функциями Лежандра, которые входят в аналитический вид
сферической функции. Для вычислений значений полиномов, и выполнения ряда
аналитических выкладок весьма полезными являются некоторые свойства
полиномов, на которых мы здесь остановимся.
Рекуррентная формула
позволяет вычислить полином степени, если известны
значения полиномов
и степеней
(4.1)
Производящая функция полиномов Лежандра
используется в представлении
потенциала притяжения рядом по сферическим функциям. Она имеет вид
(4.2)
4.1.1 Ортогональность сферический функций
Ортогональность полиномов Лежандра определяется формулой
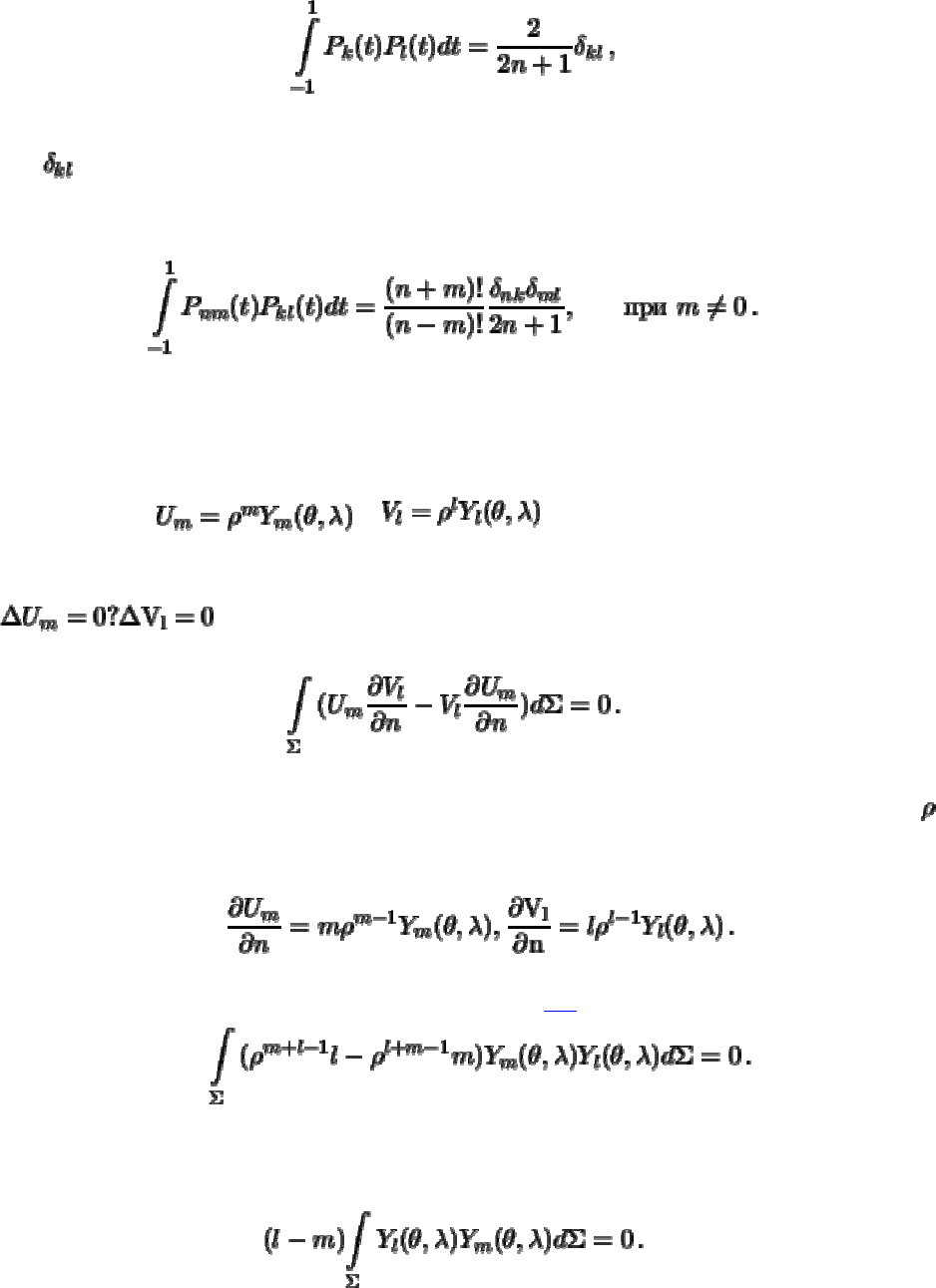
(4.3)
где
-- символ Кронекера. Присоединенные функции Лежандра также обладают
свойством ортогональности. Из теории специальных функций известно, что
(4.4)
Сферические функции также образуют класс ортогональных функций. Докажем
свойство
ортогональности сферических функций.
Возьмем две шаровые функции
первого рода
и .
Применим к ним вторую формулу Грина для сферы. Учитывая, что
, формула Грина принимает вид
(4.5)
Для сферы производная по нормали совпадает с производной по радиус-вектору
,
поэтому
Подставляя полученные выражения в формулу (
4.5), будем иметь
Поскольку радиус-вектор -- постоянная величина, полученное выражение можно
переписать в следующем виде
(4.6)

При приведенный интеграл равен нулю, что указывает на ортогональность
сферических функций.
Вернемся теперь к сферическим функциям степени , заданной в общем виде
(4.7)
Функции вида
(4.8)
называются
сферическими гармониками
. Очевидно, что ,
. Можно показать, что
(4.9)
Все основные выкладки можно найти в учебниках по специальным функциям.
4.2 Нормированные сферические функции
Как мы видели, средние значения квадратов сферических гармоник достаточно
сложно выражаются через постоянные
и . Однако, каждую из гармоник можно
умножить на постоянные так, чтобы интегралы в формулах (
4.9) были равны
единице. Эта операция называется
нормировкой.
Обозначая чертой сверху
нормированные функции, можно записать
где -- нормировочный множитель. Выберем его так, чтобы выполнялись
равенства
(4.10)
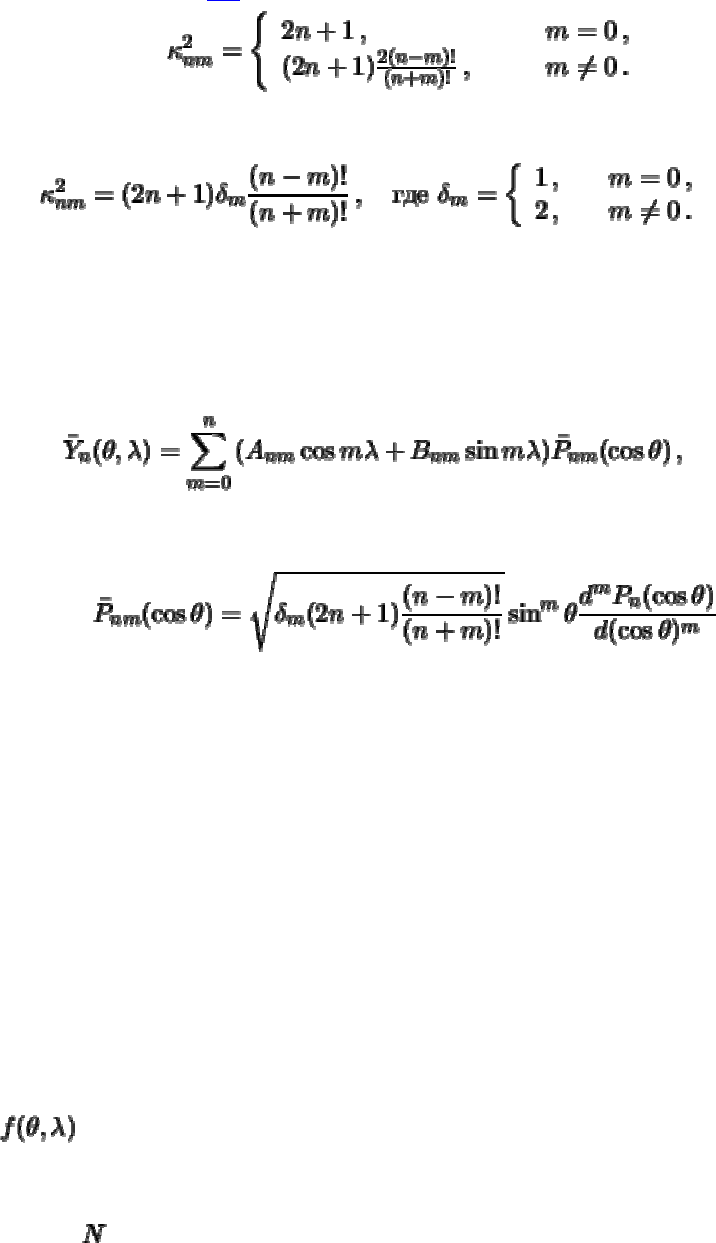
Обращаясь к формулам (4.9) легко устанавливаем, что
Полученную формулу можно переписать следующим образом
(4.11)
Операции нормировки подвергают не только сферические гармоники, но и полиномы
и функции Лежандра. В частности, если нормированная сферическая функция имеет
вид
(4.12)
то
4.3 Аналитическое представление функции, заданной на
поверхности сферы, рядом Лапласа
Свойство ортогональности сферических функций делает их незаменимыми для
аналитического представления физического поля, рельефа или других величин,
заданных в виде карты на сферической поверхности. Сферические функции играют
ту же роль, что и тригонометрические для приближенного представления
произвольной функции, заданной на отрезке рядом Фурье. Ряд, заданный в виде
суммы сферических гармоник, иногда называют рядом Лапласа.
Пусть
-- известная, кусочно-непрерывная функция, заданная в сферических
координатах. Аппроксимацию этой функции зададим в виде конечного ряда,
содержащего
сферических гармоник

(4.13)
Определим коэффициенты этого разложения так, чтобы функция
аппроксимировала функцию с наименьшим среднеквадратическим
отклонением
(4.14)
Для определения коэффициентов
и воспользуемся условиями
где
и , заданные числа. Выполняя дифференцирование, с учетом (4.13), получим
(4.15)
В полученные выражения нужно подставить вместо
правую часть формулы
(
4.13), заменив в ней индексы суммирования и на и . Мы получим интегралы
вида
Вследствие ортогональности сферических гармоник только те из интегралов отличны
от нуля, которые содержат произведения одноименных гармоник с одинаковыми
индексами. Выполнив операции, получим
(4.16)

Итак, наилучшая средняя квадратическая аппроксимация функции заданной
на сфере, многочленом, составленным из нормированных сферических гармоник
степени и порядка , имеет вид
(4.17)
где
-- нормированная присоединенная функция Лежандра.
Специальное исследование показало, что наш ряд при неограниченном увеличении
числа членов при некоторых дополнительных условиях, накладываемых на функцию
, сходится. Однако, исследование скорости этой сходимости лежит за
пределами нашего курса.
4.3.1 Интегральная форма ряда Лапласа
Мы уже говорили, что разложения вида (4.17) есть аналог ряда Фурье, в котором
роль тригонометрических функций выполняют сферические функции. Существует
также и аналог интеграла Фурье -- интегральная форма ряда Лапласа. Для того,
чтобы ее получить, подставим в (
4.17) постоянные и , которые
определятся с помощью интегралов (
4.16). Переменные, по которым производится
интегрирование мы будем помечать штрихом. Таким образом
Принимая во внимание, что
получим
(4.18)
