Легостаев Н.С., Четвергов К.В. Методы анализа и расчета электронных схем (МАРЭС). Руководство к организации самостоятельной работы
Подождите немного. Документ загружается.

80
λ
1
augment matrix 1 Ly, f,()n
вх
,
()
T
:=
λ
2
augment matrix 1 Ly, f,()n
вых
,
()
T
:=
λ
1
0123456789101112131415161718
0
0000000000000100000
=
λ
2
0123456789101112131415161718
0
0000000000000000001
=
Определение коэффициента передачи по напряжению
в соответствии с формулой (6.18)
k
U
p()
Rn SumCofactor W p( ) Converter θ
вх
(
)
, Converter λ
вых
T
⎛
⎝
⎞
⎠
,
⎛
⎝
⎞
⎠
⋅
Wp()
Rn SumCofactor W p( ) Converter θ
вых
()
, Converter λ
вых
T
⎛
⎝
⎞
⎠
,
⎛
⎝
⎞
⎠
⋅+
−:=
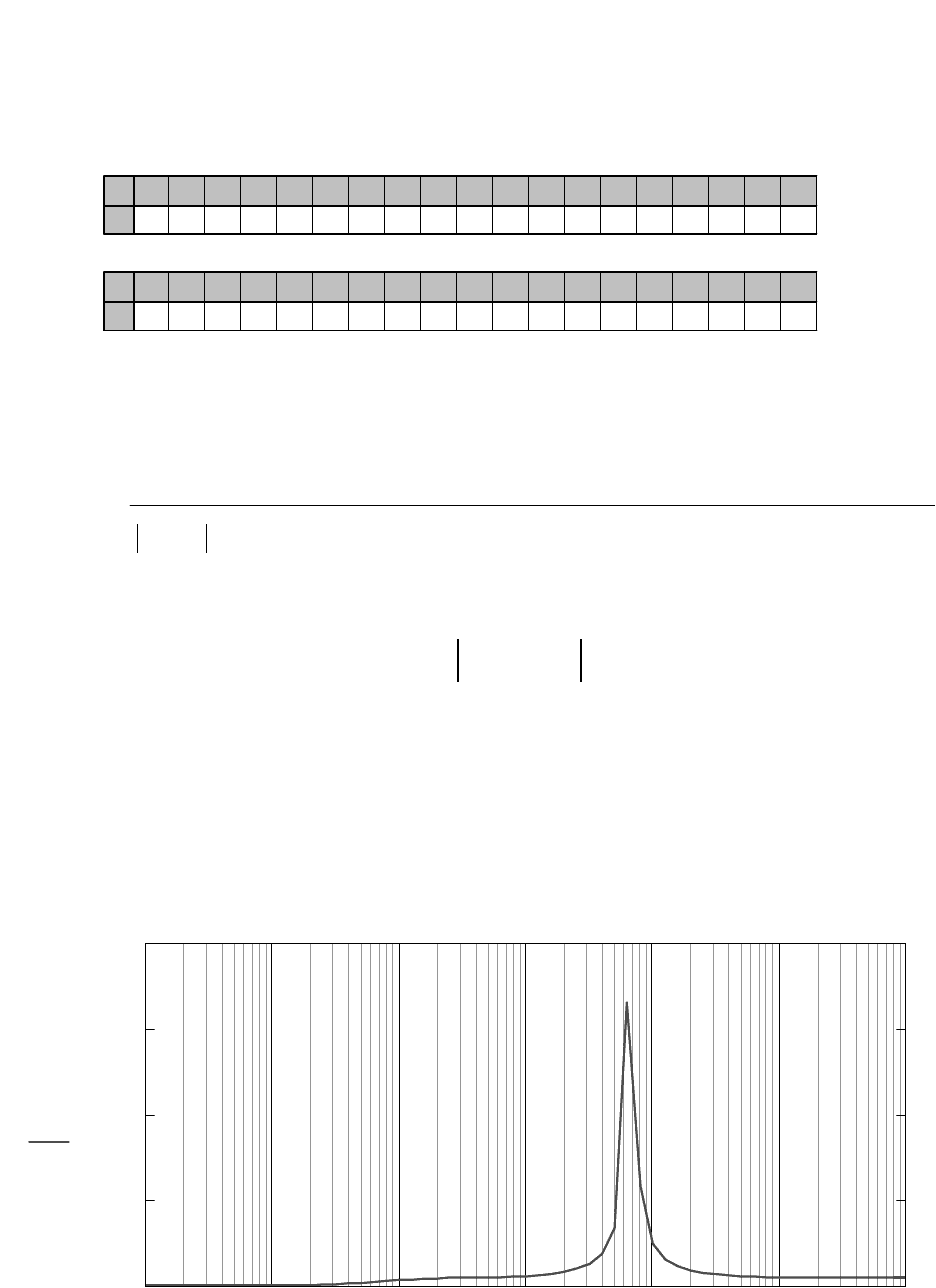
Определение АЧХ коэффициента передачи по напряжению
A
U
ω
(
)
k
U
1i ω⋅
(
)
:=
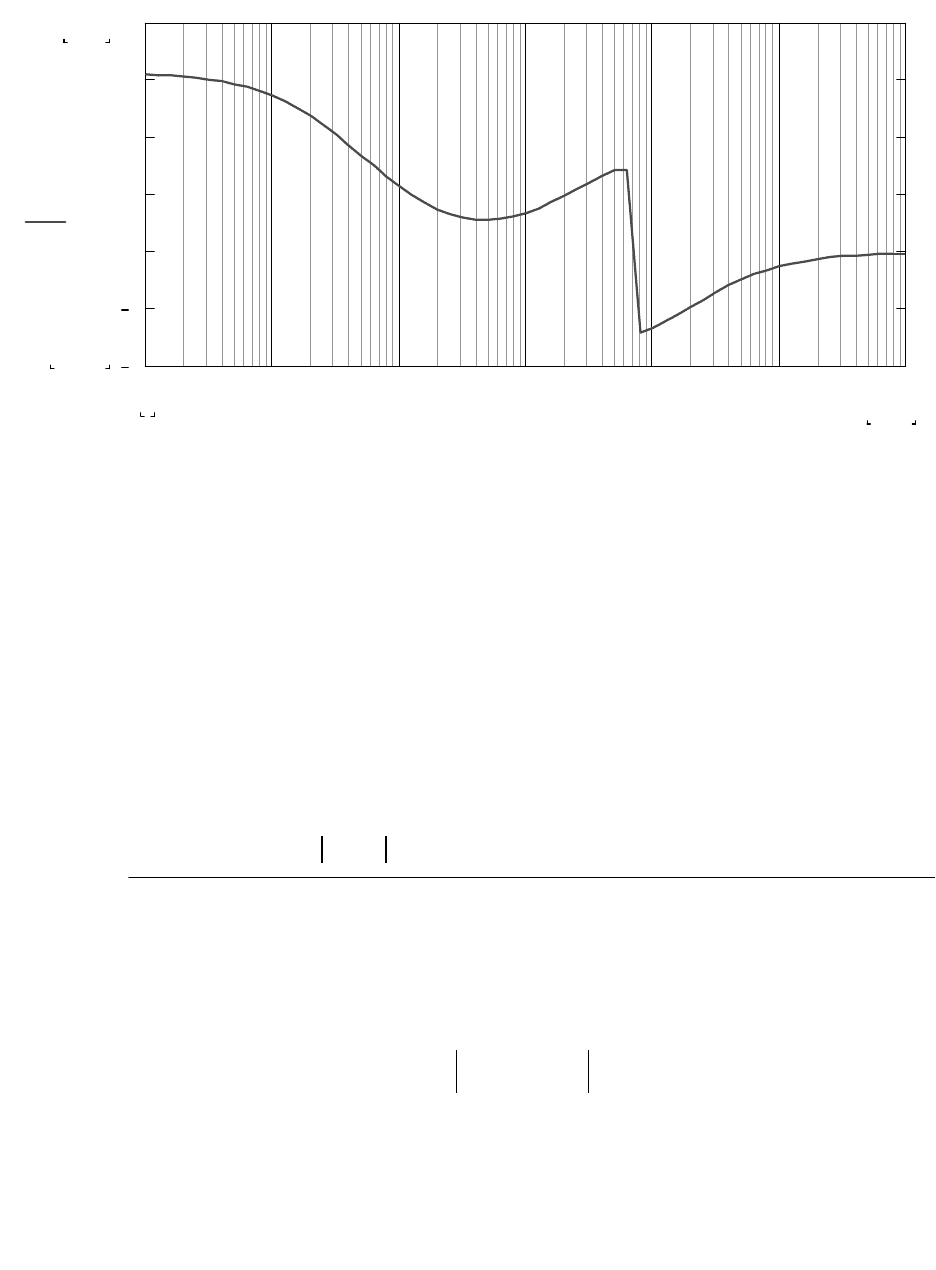
Определение ФЧХ коэффициента передачи по напряжению
φ
U
ω
(
)
arg k
U
1i ω⋅
(
)
(
)
:=
Графики АЧХ и ФЧХ коэффициента передачи по напряжению
lw 0 0.1, 6..:=
1 10 100 1
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
0
10
20
30
40
A
U
10
lw
()
10
lw
81
1 10 100 1
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
2
1
0
1
2
3
4
3.099
1.416−
φ
U
10
lw
()
1
10
6
×
1
10
lw
Определение входного импеданса в соответствии
с формулой (6.19)
θ
1
Converter
θ
вх
(
)
:=
θ
2
Converter
θ
вых
(
)
:=
λ
1
Converter
λ
вх
T
⎛
⎝
⎞
⎠
:=
λ
2
Converter
λ
вых
T
⎛
⎝
⎞
⎠
:=
Z
вх
p()
Wp()
Rn SumCofactor W p()θ
2
,λ
2
,
(
)
⋅+
SumCofactor W p()θ
1
,λ
1
,
()
Rn SumCofactorDouble W p()θ
1
,λ
1
,θ
2
,λ
2
,
()
⋅+
−:=
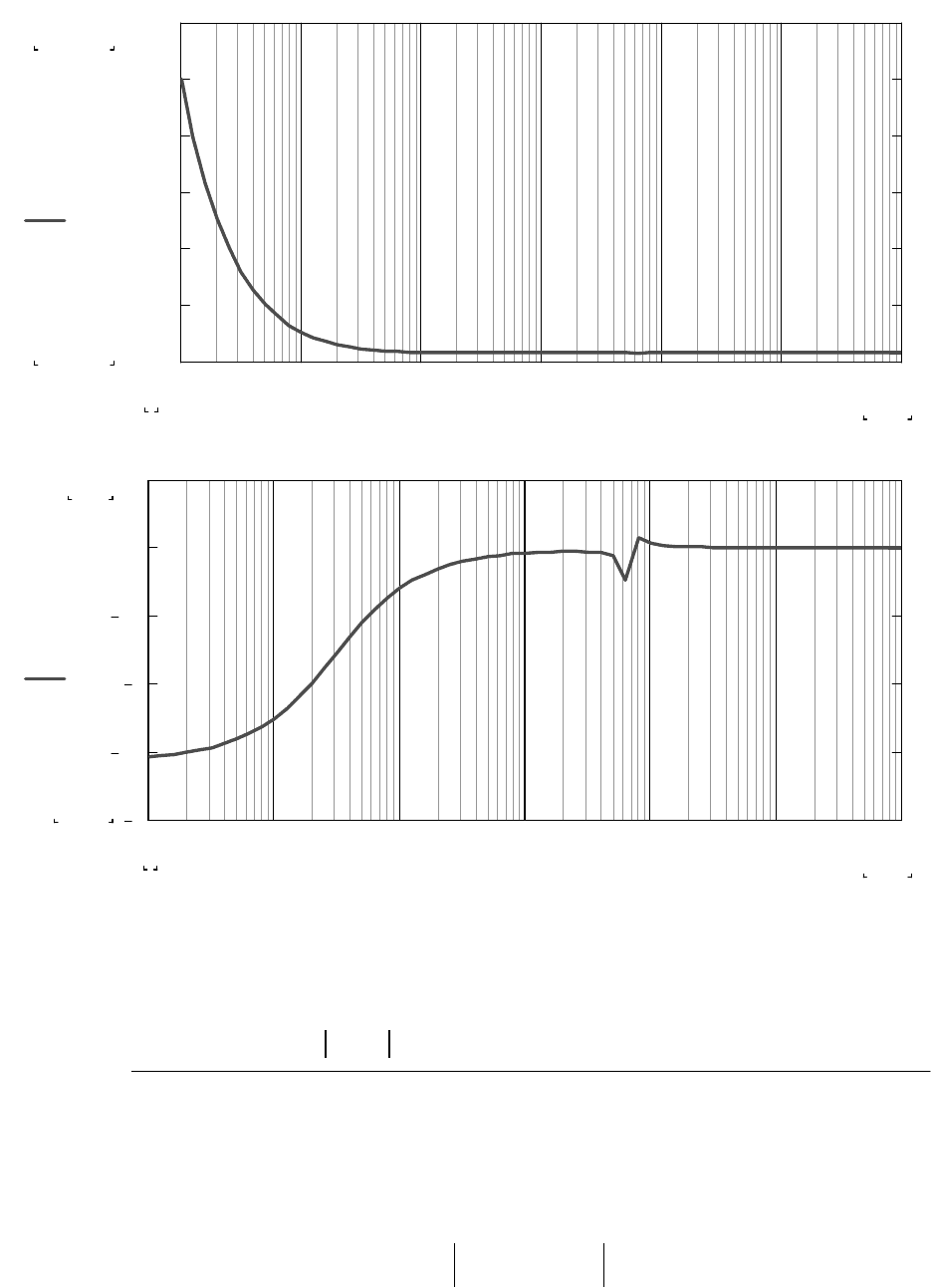
Определение АЧХ входного импеданса
A
вх
ω
(
)
Z
вх
1i ω⋅
(
)
:=
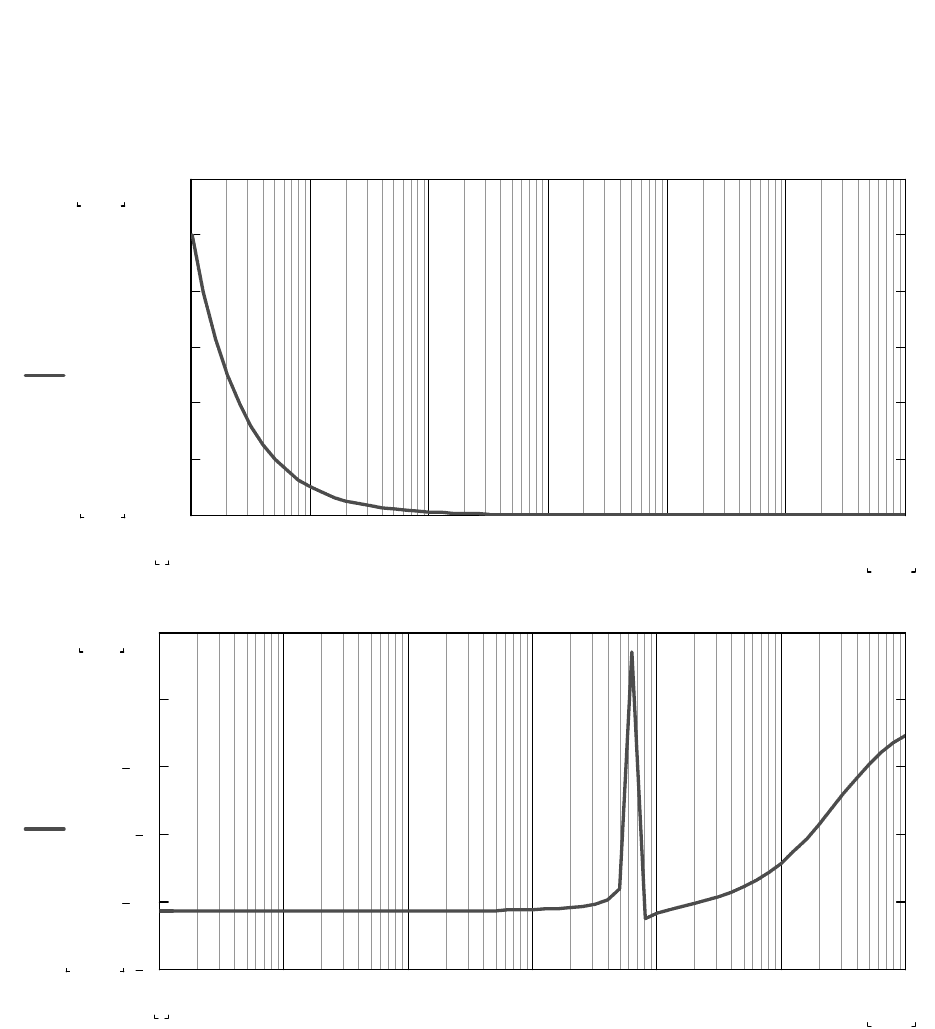
Определение ФЧХ входного импеданса
φ
U
ω
(
)
arg k
U
1i ω⋅
(
)
(
)
:=
82
Графики АЧХ и ФЧХ входного импеданса
1 10 100 1
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
0
2
.
10
4
4
.
10
4
6
.
10
4
8
.
10
4
1
.
10
5
1.2
.
10
5
1.001 10
5
×
3.152 10
3
×
A
вх
10
lw
()
1
10
6
×
1
10
lw
1 10 100 1
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
2
1.5
1
0.5
0
0.5
0.077
1.538−
φ
вх
10
lw
()
1
10
6
×
1
10
lw
Определение выходного импеданса в соответствии
с формулой (6.20)
Z
вых
p()
Wp()
rc SumCofactor W p()θ
1
,λ
1
,
(
)
⋅−
SumCofactor W p()θ
2
,λ
2
,
()
rc SumCofactorDouble W p()θ
1
,λ
1
,θ
2
,λ
2
,
()
⋅−
:=
Определение АЧХ выходного импеданса
A
вых
ω
(
)
Z
вых
1i ω⋅
(
)
:=
83
Определение ФЧХ выходного импеданса
φ
вых
ω
(
)
arg Z
вых
1i ω⋅
(
)
(
)
:=
Графики АЧХ и ФЧХ выходного импеданса
1101001
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
0
2
.
10
4
4
.
10
4
6
.
10
4
8
.
10
4
1
.
10
5
1.2
.
10
5
110
5
×
0.462
A
вых
10
lw
()
1
10
6
×
1
10
lw
1 10 100 1
.
10
3
1
.
10
4
1
.
10
5
1
.
10
6
2
1.5
1
0.5
0
0.5
0.358
1.629−
φ
вых
10
lw
()
1
10
6
×
1
10
lw
84
Определение схемных функций методом эквивалентных
схем на основе уравнений ветвей для координат (ВК-урав-
нений) в полном координатном базисе (ПКБ)
Для
формирования математической модели в виде уравнений
ветвей для координат будем использовать полную систему незави-
симых сечений и контуров, соответствующую системе координат,
выбранной при формировании координатных уравнений для ветвей
и показанную на графе рис. 6.15. В этом случае все топологические
и компонентные матрицы и уравнения уже составлены при форми-
ровании координатных уравнений для ветвей.
В полном координатном базисе напряжения и токи y-ребер,
а также напряжения и токи z-ребер связаны с напряжениями не-
зависимых сечений и токами независимых контуров соотноше-
ниями:
UU
T
yy
Π=
,
UU
T
z
z
Π=
,
II
T
yy
Ρ=
,
II
T
z
z
Ρ=
,
которые можно представить в обобщенной матричной форме
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
Ρ
Π
=
⎥
⎦
⎤
⎢
⎣
⎡
I
U
I
U
T
z
T
y
z
y
0
0
,
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
Π
Ρ
=
⎥
⎦
⎤
⎢
⎣
⎡
I
U
U
I
T
z
T
y
z
y
0
0
или
X
X
T
Θ=
′
,
XX
T
1
Θ=
′′
, (6.43)
где
[]
T
UUUUUUUUUUU
10987654321
=
— вектор напря-
жений независимых сечений;
[]
T
IXVIIIVIIVIVIVIIIIII
IIIIIIIIII = — вектор токов
независимых контуров;
⎥
⎦
⎤
⎢
⎣
⎡
=
I
U
X
— обобщенный вектор состояния, определяемый
независимыми сечениями и контурами.
Для формирования системы уравнений ветвей для коорди-
нат необходимо в обобщенном компонентном уравнении (6.2)
85
векторы
X
′
и
X
′
′
выразить через вектор
X
, используя выражения
(6.43):
(
)
FXV
TT
−=−
1
ΘΘ
или
Q
WX
=
, (6.44)
где
TT
VW
1
ΘΘ −=
— матрица эквивалентных параметров;
F
Q
−=
— обобщенный вектор внешних воздействий.
Схема замещения рис. 6.4 содержит два задающих источни-
ка э.д.с., расположенных во входной и выходной ветвях, поэтому
вектор задающих э.д.с.
в
E может быть представлен в виде:
[]
⎥
⎦
⎤
⎢
⎣
⎡
=
вых
вх
выхвхв
U
U
mmE
, (6.45)
где
вх
m и
вых
m — векторы-столбцы, связывающие задающие э.д.с.
вх
U и
вых
U с номерами соответствующих ребер графа, причем
T
вхвх
nm −=
,
T
выхвых
nm =
.
С учетом (6.45) матричное уравнение (6.44) может быть
представлено в виде:
[]
⎥
⎦
⎤
⎢
⎣
⎡
θθ−=
вых
вх
выхвх
U
U
WX
, (6.46)
где
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
T
вхвх
вх
nm
00
θ ,
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
T
выхвых
вых
nm
00
θ .
Входной и выходной токи связаны с токами независимых
контуров выражениями
II
T
вхвх
ρ=
,
II
T
выхвых
ρ=
,
86
которые могут быть представлены в виде матричного уравнения:
X
I
I
вых
вх
вых
вх
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
λ
λ
, (6.47)
где
[
]
T
вхвх
ρλ 0=
,
[
]
T
выхвых
ρλ 0=
.
Объединив (6.46) и (6.47) в одно матричное уравнение
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
λ
λ
θ
θ
вых
вх
вых
вх
вых
вх
выхвх
I
I
U
U
XW
0
00
00
и решив его относительно
вх
U и
вых
U , получим
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
вых
вх
вх
вх
вых
вх
вых
вх
выхвх
вых
вых
вх
вых
вх
вых
вых
вых
вх
выхвх
вх
I
W
I
W
W
U
I
W
I
W
W
U
00
00
00
1
00
00
00
1
λ
θ
λ
θ
λ
λ
θθ
λ
θ
λ
θ
λ
λ
θθ
(6.48)
Сравнивая (6.48) с (6.13), приходим к выводу, что искомые
схемные функции определяются выражениями (6.18)—(6.20).

87
Расчет АЧХ и ФЧХ избирательного RC-усилителя
с двойным Т-образным мостом в цепи обратной связи на основе
координатных уравнений для ветвей в полном координатном
базисе
Параметры полюсного графа схемы
μ'14=μ' ν' σ'+:=
μ
'' 5=μ'' ν'' σ''+:=
μ
19=μνσ+:=
σ
'5=σ' σσ''−:=
ν
'9=
ν
' νν''−:=
σ
'' 4=σ'' Ly υ− ny+:=
ν
'' 1=ν'' ny n−:=
σ
9=σ Ly Lz+()υ− n+:=
ν
10=νυn−:=
ny
2
:=n1:=υ 11:=Lz 6:=Ly 13:=
Топологические матрицы
Π'
y
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
−
1
1
−
0
0
0
1
−
0
0
0
0
1
0
0
0
0
0
0
0
0
1
1
−
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
−
0
0
0
0
0
0
0
0
1
−
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=

88
Π'
z
1
−
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
−
1−
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
−
1
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Π''
z
1− 11000(
)
:=
Π
y
stack
Π'
y
matrix ν'' Ly, f,
()
,
(
)
:= Π
z
stack
Π'
z
Π''
z
,
()
:=
P'
y
1
0
0
0
0
0
0
1
0
0
0
0
1
−
1−
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
−
0
0
0
0
1
0
0
0
0
0
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎠
:= P'
z
1
0
0
0
0
0
1
0
0
0
1
1
−
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎠
:=
P''
y
0
0
0
0
0
0
0
0
1
−
0
0
0
1
0
0
0
1
0
0
0
1
1
−
0
0
0
1
0
0
0
1
1
−
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
1
−
0
1
−
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
P
y
stack P'
y
P''
y
,
()
:= P
z
stack P'
z
matrix σ'' Lz, f,
()
,
()
:=
Обобщенные топологические матрицы
Θ stack augment Π
y
matrix
ν Lz, f,
(
)
,
()
augment matrix σ Ly, f,
(
)
P
z
,
(
)
,
()
:=
Θ
1
stack augment matrix
ν Ly, f,
()
Π
z
,
()
augment P
y
matrix σ Lz, f,
()
,
()
,
()
:=
89
Компонентные матрицы
Yp()
pC1
⋅
0
0
0
0
0
0
0
0
0
0
0
0
0
ge'
0
0
0
0
0
0
0
0
0
0
0
0
0
1
R4
0
0
0
0
0
0
0
0
0
0
0
0
0
1
rk
0
0
0
0
0
0
0
0
0
0
0
0
0
1
rb
0
0
0
0
0
0
0
0
0
0
0
0
0
pC2
⋅
0
0
0
0
0
0
0
0
0
0
0
0
0
1
R5
0
0
0
0
0
0
0
0
0
0
0
0
0
pC3
⋅
0
0
0
0
0
0
0
0
0
0
0
0
0
1
R7
0
0
0
0
0
0
0
0
0
0
0
0
0
pC4
⋅
0
0
0
0
0
0
0
0
0
0
0
0
0
ge''
0
0
0
0
0
0
0
0
0
0
0
0
0
pC5
⋅
0
0
0
0
0
0
0
0
0
0
0
0
0
1
R6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Zp()
0
0
0
0
0
0
0
R
б
0
0
0
0
0
0
h11'
0
0
0
0
0
0
re
0
0
0
0
0
0
h11''
0
0
0
0
0
0
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
