Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


can
be
obtained
from
the
other
by
a
finite
number
of
spherical
modifications.
A
well
written
introductory
book
is
Wallace
(1968].
Hirsch
(1976]
has
a
couple
of
chapters
discussing
surgery
(also
called
cobordism
in
literature).
A
very
advanced
classic
is
the
one
by
Wall
(1970].
There
may
be
revised
edition.
There
were
some
potential
applications
in
physics
the
author
thought
of
while
he
was
a
graduate
student.
However,
the
author
has
not
been
following
the
developments
lately.
It
seems
that
it
may
also
be
useful
for
the
description
of
super-strings
in
particle
physics.
Before
we
are
too
far
off
the
field
from
the
subject
of
nondegenerate
critical
points,
let
us
look
at
some
of
its
properties
from
the
Morse
Lemma.
It
has
been
known
for
some
time
that
a
topological
space
may
be
characterized
by
the
algebra
of
continuous
functions
on
it.
From
the
examples
given
earlier,
it
is
not
surprising
that
one
can
learn
a
great
deal
about
a
smooth
manifold
from
the
smooth
real
functions
defined
on
it.
Morse
(1934]
first
realized
the
importance
of
nondegenerate
critical
points
and
the
numerical
invariant
called
the
index,
which
completely
characterizes
the
local
behavior
near
that
point.
Moreover,
the
number
of
critical
points
of
various
indexes
relates
to
the
topology
of
a
manifold
by
means
of
the
Morse
inequalities.
A
sufficiently
isolated
critical
point
also
signals
the
addition
of
a
cell
to
the
decomposition
of
the
manifold.
Thus,
this
shows
how a
manifold
is
put
together
as
a
cell
complex,
in
terms
of
the
critical
points
of
a
sufficiently
well-behaved
function.
Furthermore,
from
Sard's
theorem
(Theorem
2.5.3),
these
well-behaved
functions
are
actually
very
common.
In
the
rest
of
this
section,
we
will
discuss
the
Morse
lemma
and
inequalities,
and
transversality
properties.
A
symmetric
bilinear
form
represented
by
a
matrix
B
has
index
i
if
B
has
i
negative
eigenvalues.
We
asy
that
B
has
nullity
k
if
k
of
the
eigenvalues
are
zero.
Thus,
p
is
a
nondegenerate
critical
point
for
f when p
is
a
critical
point
and
the
nullity
of
the
Hessian
of
f
at
p
is
zero.
64

Lemma
2.5.8
(Morse)
Let
M
be
n-dim
CO
manifold,
f:
M
~
R
be
smooth
and
x
0
E M a
nondegenerate
critical
point.
Then
there
is
a
coordinate
chart
Ua
containing
X
0
with
~a(x
0
)
= 0
and
such
that
f(~a-
1
(u))
=
f(~a-
1
(0))
- u
1
2
-
.•.
-
U;
2
+
u;.
1
2
+
••
+
un2.
where
u =
(u
1
,
••
,un)
e
R"
and
i
is
the
Morse
index
off
at
xo.
Corollary
2.5.9
The
non-degenerate
critical
points
of
a
smooth
function
are
isolated.
Corollary
2.5.10
If
f
is
smooth
on
a
compact
smooth
manifold
with
all
critical
points
non-degenerate,
then
f
has
only
finitely
many
critical
points.
As
an
example,
consider
the
family
of
surfaces
in
R
3
,
x2
-
Y2
-
z2
= c
with
-1
~
c
~
1.
Note
that
the
two
surfaces
obtained
by
putting
c =
-1
and
1
are
hyperboloids
of
one
and
two
sheets
respectively.
Then
the
critical
points
are
easily
obtained.
These
two
s·
are
nondegenerate
critical
points
which
are
isolated.
These
infinitely
many
critical
points
of
s
1
are
degenerate.
If
all
critical
points
of
f
are
non-degenerate
and
all
critical
values
are
distinct,
then
f
is
called
a
Morse
function.
A
fundamentally
important
result
is
the
following
set
of
Morse
inequalities:
Theorem
2.5.11
(Morse
inequalities)
Let
M
be
a
CG
compact
m-
manifold
(without
boundary)
and
f:
M
~
R
be
a
Morse
function.
Let
ck,
k =
0,1,
••
,m,
denote
the
number
of
critical
points
of
f
of
index
k
and
Pk
be
the
kth
Betti
65

number
of
M
(i.e.,
the
number
of
independent
generators
of
the
kth
homology
group
of
M).
Then
Co
0!:
Po
c
1
-
C
0
0!:
P,
-
Po
c
2
-
c
1
+ C
0
0!:
P
2
- P
1
+ P
0
C
11
- C
11
_
1
+
•••
+(-1)
11
C
0
0!:
P
11
- P
11
_
1
+
••
+(-1)
11
P
0
•
Before
we
continue,
we
would
like
to
briefly
discuss
orientation,
duality,
and
Euler
characteristics,
and
some
of
their
geometric
interpretations.
Orientation
of
a
manifold
is
of
fundamental
importance.
Duality
relates
(or
more
appropriately
pairing)
the
Betti
numbers
of
an
orientable,
compact
manifold.
Euler
characteristic
is
a
topological
invariant
quantity
built
upon
from
Betti
numbers,
and
its
existence
on
a
manifold
has
profound
geometric
implications.
For
lower
dimensional
manifolds,
in
particular,
two-dimensional
manifolds,
it
is
directly
related
to
the
curvature
of
the
2-manifold.
Proposition
2.5.12
Every
manifold
has
a
unique
Z/2
-
orientation
(the
number
of
orientation
=
no.
of
elements
in
H
0
(X,Z/2)
) •
There
are
several
ways
to
define
orientation.
The
above
is
a
topological
one.
We
shall
discuss
a
geometric
one
later.
Theorem
2.5.13
Let
X
be
a
connected
non-orientable
manifold.
Then
there
is
a
2-fold
connected
covering
space
E
P~
X
such
that
E
is
orientable.
This
theorem
tells
us
that
if
we
are
interested
in
the
detailed
local
geometry
of
the
manifold
(assumed
to
be
arcwise-
connected)
as
a
model
of
physical
state
space,
then
we
may
as
well
assume
the
manifold
to
be
orientable.
This
is
because
one
can
always
find
an
orientable
covering
space
which
has
same
local
geometry.
Indeed,
as
the
next
corollary
shows,
one
can
always
goes
to
its
universal
covering
space,
which
is
simply-connected.
Corollary
2.5.14
Every
simply-connected
X
is
orientable.
66

Proposition
2.5.15
Hn(X) = 0
if
X
is
connected
and
non-
compact,
(dim
X=
n).
Poincare
Duality
Theorem
2.5.16
If
X
is
an
oriented,
n-dim
manifold,
then
the
homomorphism
D : Hcq(X)
...
Hn-q(X)
is
an
isomorphism
for
all
q,
where
Hcq(X)
is
the
cohomology
group
with
compact
support.
We
shall
discuss
differential
forms,
and
the
de
Rham
cohomology,
and
the
cohomology
groups
of
a
manifold.
Corollary
2.5.17
If
X
is
compact,
orientable,
then
the
Betti
numbers
of
X
satisfy
bq =
bn-q
for
all
q.
The
Euler
characteristic
of
X X(X)
is
defined
as
an
alternating
sum
of
all
the
Betti
numbers
of
X,
i.e.,
X(X)=
I:
(-1)q
bq
, n
=dim
X.
Examples:
For
q
~
1,
n
~
1
Hq(S") = j
R,
q = n
o, q +
n.
Thus,
Remark:
x (X)
E.g.:
o,
n =
odd
2,
n =
even.
is
a
very
useful
topological
invariant.
Theorem
2.5.18
A
differentiable
manifold
(any
dimension)
admits
a
non-zero
continuous
vector
field
iff
its
Euler
characteristics
are
zero
[Steenrod
1951].
As
a
consequence,
we
have:
For
compact
manifold
M,
there
exists
a
non-vanishing
vector
field
iff
X(M)=
0.
Thus
only
odd-
dim
spheres
admit
non-vanishing
vector
fields.
Indeed,
one
can
prove
that
this
is
equivalent
to
that
the
tangent
bundle
of
M
splits,
which
is
also
equivalent
to
the
manifold
admits
a
metric
of
Lorentz
signature
(i.e.,pseudo-Riemannian
metric).
Since
it
is
well-known
that
any
differentiable
manifold
admits
a
Riemannian
metric,
the
Lorentz
metric
can
be
constructed
by
~(Y,Z)
=
g(Y,Z)
-
2g(X,Y)g(X,Z)/g(X,X)
or
~ii
=
gii
- 2
X;Xjll
X
I•
.
where
X, Y,
and
z
are
non-zero
vector
fields
on
M.
We
shall
come
back
to
this
later,
when
we
discuss
characteristic
classes.
67

Gauss-Bonnet
theorem
2.5.19:
Let
M
be
a
compact
connected
oriented
Riemannian
2-manifold
with
Riemannian
(Gausssian)
curvature
function
K.
Then
J K =
2~X(M)
[Hicks
1971].
Generalized
Gauss-Bonnet
Theorem
2.5.20:
If
M
is
an
even
dimension
(n
=
2k)
compact
connected
oriented
Riemannian
manifold,
then
JM
Q =
2"~k(k!)X(M)
where
Q =
:E(-1)'~'R,.<1>•mhR.<3>
..
<4>A.
•
·AR.<n-1>
..
<n>
€ A"(M)
where
~(i)
are
permutations
[Chern
1951].
Let
us
get
back
to
the
Morse
lemma
and
Morse
inequalities.
If
furthermore,
M
is
orientable,
then,
applying
the
Poincare
duality
theorem,
we
can
further
simplify
the
inequalities.
As
an
example,
if
M = T
2
,
the
2-dim
torus,
then
any
Morse
function
on
T
2
has
at
least
four
distinct
critical
points
since
P
0
= P
2
= 1
and
P
1
=
2.
We
have
already
demonstrated
and
discussed
this
earlier.
Let
us
get
back
to
Sard's
theorem.
Although
many
arguments
in
imbedding
and
immersion
can
be
reformulated
and
occasionally
made
more
precise
by
using
Sard's
theorem,
we
shall
turn
to
a
very
important
concept
of
transversality.
This
is
a
theory
which
investigates
the
way
submanifolds
of
a
manifold
cross
each
other.
Let
f
be
c"'
map
of
c"'
manifolds,
f:
M"'
-+
N",
and
WP
be
a
submanifold
of
N.
Roughly
speaking,
f
is
transverse
to
W
at
x €
M,
f~x
W,
means
that
the
intersection
inN
of
f(M)
and
W
has
the
lowest
possible
dimension
in
a
neighborhood
of
f(x)
€
W,
but
the
sum
of
the
dimensions
of
f(M)
and
W
is
at
least
n.
More
precisely:
Given
a
c"'
map
f:
M"'
-+
N"
between
two
c"'
manifolds
and
a
submanifold
wP
of
N,
we
say
f
is
transverse
to
W
if
for
each
x €
M,
y =
f(x)
€ W
such
that
df(Mx)
+
WY
=
NY.
Here
+
means
that
we
take
the
set
of
all
vectors
in
NY
that
are
sums
of
a
vector
in
the
image
of
df
and
a
tangent
vector
to
the
submanifold
W.
In
other
words,
the
tangent
space
NY
is
spanned
by
WYand
the
image
df(Wx>·
If
f(M)
does
not
intersect
W,
i.e
. ,
f(M)
n W =
0,
then
f
is
automatically
transverse
to
W.
As
a
simple
example,
let
M = s
1
,
N = R' , w =
x-axis
in
68
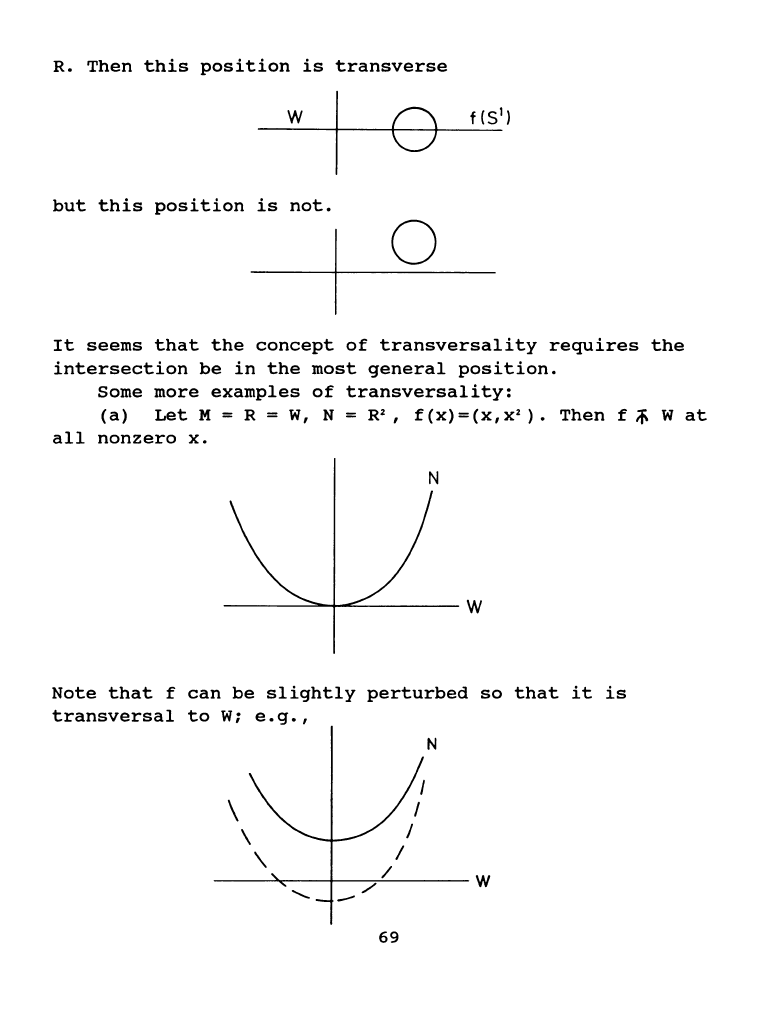
R.
Then
this
position
is
transverse
w
8
but
this
position
is
not.
0
It
seems
that
the
concept
of
transversality
requires
the
intersection
be
in
the
most
general
position.
Some
more
examples
of
transversality:
(a)
Let
M = R =
W,
N = R
2
,
f(x)=(x,x
2
).
Then
f
~
W
at
all
nonzero
x.
N
Note
that
f
can
be
slightly
perturbed
so
that
it
is
transversal
toW;
e.g.,
N
69

(b)
M,
N, W
as
in
(a)
and
f
is
defined
by
the
graph
N
w
Then
f ; W
everywhere
except
on
the
segments
within
the
brackets.
(c)
If
M = W =
R,
N = R
3
,
then
if
f
is
any
mapping
of
M
~
N,
it
is
transversal
to
W
only
if
f(M)
n W = o.
Note
that
here
a
nontransversal
mapping
can
also
be
approximated
closely
by
a
transversal
mapping
because
in
3-space
f
can
avoid
W
even
easier
by
just
going
around
it
and
f
only
has
to
move
a
little
bit
to
accomplish
this.
We
shall
make
this
more
precise
in
the
next
proposition.
From
these
simple
examples,
it
becomes
apparent
that
the
relative
dimensions
of
M,
N
and
W
play
an
important
role
in
determining
the
conditions
as
well
as
meaning
for
f
to
be
transversal
to
W.
Moreover,
for
any
M,
N
and
W,
the
set
of
transversal
mappings
is
a
very
large
one.
Them's
transversality
theorem
is
a
formalized
observation
of
this
fact.
Before
discussing
Thorn's
theorem,
we
first
give
some
properties
of
the
set
of
maps
which
is
transversal
to
w.
Proposition
2.5.21
Let
M
and
N
be
smooth
manifolds,
W c
N a
submanifold.
Suppose
dim
W +
dim
M <
dim
N.
Let
f : M
~
N
be
smooth
and
suppose
that
f
~
w.
Then
f(M)
n w = o.
This
can
be
seen
by
the
fact
that
suppose
f(p)
€
W,
then
by
the
definition
of
tangent
space
and
the
assumption,
dim(Wf<p> +
(df)
(MP)) 5
dim
Wf<p>
+
dim
MP
=
dim
W +
dim
M <
dim
N =
dim
Nf<x>'
thus
it
is
impossible
for
Wf<x>
+
df
(MP)
=
Nf<x>.
Thus
if
f
if\
W
at
p,
then
f(x)
f
W.
It
is
also
appropriate
for
us
to
relate
the
notion
of
70
transversality
with
Sard's
theorem.
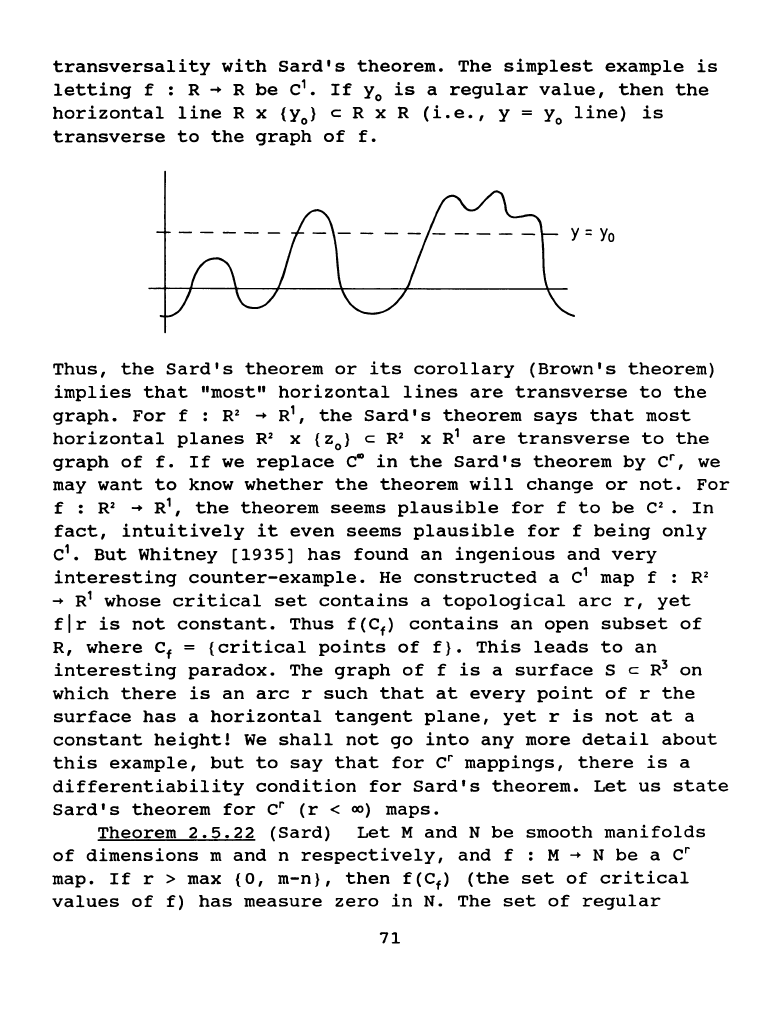
The
simplest
example
is
letting
f : R
~
R
be
c
1
•
If
y
0
is
a
regular
value,
then
the
horizontal
lineR
x
{y
0
}
c R x R
(i.e.,
y = y
0
line)
is
transverse
to
the
graph
of
f.
Y
=Yo
Thus,
the
Sard's
theorem
or
its
corollary
(Brown's
theorem)
implies
that
"most"
horizontal
lines
are
transverse
to
the
graph.
For
f : R
2
~
R
1
,
the
Sard's
theorem
says
that
most
horizontal
planes
R
2
x {z
0
}
c R
2
x R
1
are
transverse
to
the
graph
of
f.
If
we
replace
~
in
the
Sard's
theorem
by
c•,
we
may
want
to
know
whether
the
theorem
will
change
or
not.
For
f : R
2
~
R
1
,
the
theorem
seems
plausible
for
f
to
be
c•.
In
fact,
intuitively
it
even
seems
plausible
for
f
being
only
c
1
•
But
Whitney
[1935)
has
found
an
ingenious
and
very
interesting
counter-example.
He
constructed
a c
1
map f : R
2
~
R
1
whose
critical
set
contains
a
topological
arc
r,
yet
fir
is
not
constant.
Thus
f(C
1
)
contains
an
open
subset
of
R,
where
c
1
=
{critical
points
of
f}.
This
leads
to
an
interesting
paradox.
The
graph
of
f
is
a
surface
s c R
3
on
which
there
is
an
arc
r
such
that
at
every
point
of
r
the
surface
has
a
horizontal
tangent
plane,
yet
r
is
not
at
a
constant
height!
We
shall
not
go
into
any
more
detail
about
this
example,
but
to
say
that
for
c•
mappings,
there
is
a
differentiability
condition
for
Sard's
theorem.
Let
us
state
Sard's
theorem
for
c•
(r
<
~>
maps.
Theorem
2.5.22
(Sard)
Let
M
and
N
be
smooth
manifolds
of
dimensions
m
and
n
respectively,
and
f : M
~
N
be
a
c•
map.
If
r
>max
{0,
m-n},
then
f(Cf)
(the
set
of
critical
values
of
f)
has
measure
zero
in
N.
The
set
of
regular
71

values
off
is
dense
••
Theorem
2.5.23
Let
f,
M,
N
and
W
as
before.
If
f
is
transverse
toW,
then
f"
1
(W)
is
a
submanifold
of
M
with
dimension
m - n +
p.
Corollary
2.5.24
If
M
and
W
are
both
submanifolds
of
N
and
for
each
x E M n W
such
that
Wx
+
Mx
=
Nx.
Then
M n W
is
a
submanifold
of
N.
Before
we
can
get
to
Them's
Transversality
theorem,
we
need
some
refinement
on
the
topology
of
the
space
of
differentiable
maps
between
differentiable
manifolds.
Let
c"'(R",Rk)
be
the
set
of
c"'-maps
(or
c"'-functions)
from
R"
to
Rk.
The
set
is
topologized
as
follows:
If
e(x)
is
a
positive,
continuous
function
defined
on
R",
and
p > 0
is
any
integer,
let
B(O,e(x)
,p)
= (fec"'(R",Rk) I
ln«fi(x)
l<e(x)
for
all
lals
p
and
j}
where
fi
is
the
j-th
coordinate
of
f.
This
set
forms
a
basis
for
the
neighborhood
of
the
constant
function
o. A
similar
basis
neighborhood
for
g E c"'(R",Rk)
can
be
defined
by
B(g,e(x)
,p)
=
(f
E c"'(R",Rk) I
(f-g)
E
B(O,e(x)
,p)
}.
Here
the
integer
p
is
allowed
to
vary.
To
generalize
the
topology
of
c"'
(M"',
N")
,
where
M"',
N"
are
two
c"'-manifolds,
one
can
proceed
as
above
by
choosing
coordinate
charts
to
cover
N"
and
demand
that
the
above
construction
holds
in
all
the
coordinate
charts
near
any
point.
Of
course
one
may
also
reduce
this
problem
to
the
above
construction
in
much
larger
Euclidean
spaces
by
using
the
imbedding
theorem.
We
want
to
point
out
that
the
above
construction
provides
a
rather
fine
topology
on
c"'(M"',N"),
this
is
because
function
such
as
e(x)
may
decrease
to
zero
rapidly,
even
though
e(x)
> 0
for
all
x.
Theorem
2.
5.
2 5
Let
M"',
N"
be
c"'
manifolds,
and
WP
N"
a
submanifold.
The
set
Fw(M"',N"),
consisting
all
maps
in
c"'(M"',N")
that
are
transverse
to
W,
is
an
open
subset
of
c"'
(M"'
IN")
•
Theorem
2.5.26
(Them's
transversality
theorem)
Fw(M"',N")
is
dense
in
c"'
(M"',
N")
•
72

The
transversality
theorem
in
its
many
variations
are
not
only
of
fundamental
importance
to
structural
stability
and
bifurcations,
but
are
also
of
crucial
importance
to
many
areas
of
differential
topology
such
as
Thom•s
construction
of
cobordism
theory.
Two
compact
manifolds
M
1
,
M
2
are
called
cobordant,
if
there
is
a
compact
manifold
N
such
that
aN
~
{M
1
x
0}
U
{~
x
1}.
Loosely
speaking,
this
means
that
the
disjoint
union
of
M
1
and
M
2
is
the
boundary
of
N.
We
call
N
a
cobordism
from
M
1
to
M
2
•
The
spherical
modification
we
mentioned
earlier
is
a
special
situation
of
cobordism
theory.
In
the
next
section,
we
shall
discuss
more
geometric
details
of
a
differentiable
manifold,
in
particular,
the
group
actions
on
manifolds.
This
will
provide
the
fundation
for
the
discussion
of
fiber
bundles,
which
is
the
section
after
next.
2.6
Group
and
group
actions
on
manifolds,
Lie
groups
Lie
groups
exist
naturally
in
many
areas
of
mathematics
and
physics
where
natural
group
structures
may
be
found
on
certain
manifolds.
Lie
groups
are
also
very
useful
in
physics,
in
particular,
as
transformation
groups,
internal
symmetry
groups
and
their
representations
for
particle
classifications,
gauge
groups,
etc.
Even
in
classical
mechanics,
the
usual
Lagrange
and
Poisson
bracekets
not
only
provide
the
system•s
symmetry
or
conservation
laws,
but
also
provide
a
geometric
manifestation
of
the
dynamical
processes
by
noticing
that
a
Poisson
bracket
of
a
pair
of
vector
fields
is
the
dragging
of
a
vector
field
along
the
integral
curve
of
another
vector
field.
There
are
many
well
written
books
on
Lie
groups.
As a
beginning,
many
differential
geometry
books
have
a
chapter
or
two
on
Lie
groups,
their
geometry,
and
representations,
e.g.,
Bishop
and
Crittenden
[1964].
There
are
several
sections
in
various
chapters
of
Choquet-Bruhat,
De
Witt-Morette
and
Dillard-Bleick
[1977].
For
more
advanced
readers,
Chevalley
[1946]
is
still
the
73
