Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

-26 Robotics and Automation Handbook

[26] Phillips, C.L. and Nagle, H.T., Digital Control System Analysis and Design, Prentice Hall, Englewood

Cliffs, NJ, 1995.

[27] Van Beek, B. and De Jager, B., RRR-robot design: Basic outlines, servo sizing, and control, in Proc.

IEEE Int. Conf. Control Appl., Hartford, U.S.A., 1997, 36.

[28] Van Beek, B. and De Jager, B., An experimental facility for nonlinear robot control, in Proc. IEEE

Int. Conf. Control Appl., Hawaii, U.S.A., 1999, 668.

[29] Kosti

c, D., Hensen, R., De Jager, B., and Steinbuch, M., Modelingand identiﬁcation of an RRR-robot,

in Proc. IEEE Conf. Dec. Control, Orlando, FL, 2001, 1144.

[30] Kosti

c, D., Hensen, R., De Jager, B., and Steinbuch, M., Closed-form kinematic and dynamic models

of an industrial-like RRR robot, in Proc. IEEE Conf. Rob. Autom., Washington D.C., 2002, 1309.

[31] Kosti

c, D., De Jager, B., and Steinbuch, M., Experimentally supported control design for a direct

drive robot, in Proc. IEEE Int. Conf. Control Appl., Glasgow, Scotland, 2002, 186.

[32] Kosti

c, D., De Jager, B., and Steinbuch, M., Robust attenuation of direct-drive robot-tip vibrations,

in Proc. IEEE/RSJ Int. Conf. Intellig. Robots Syst., Lausanne, Switzerland, 2002, 2206.

Motion Control by

Linear Feedback

Methods

Dragan Kosti

Technische Universiteit Eindhoven

Bram de Jager

Technische Universiteit Eindhoven

Maarten Steinbuch

Technische Universiteit Eindhoven

15.1 Introduction

15.2 Decentralized Conventional Feedback Control

15.3 Linear Feedback Control Applied with Nonlinear

Model-Based Dynamic Compensators

Computed-Torque Control Design

•

Control Designs with

Feedback Linearization

15.4 Case-Study: Motion Control of the RRR

Direct-Drive Manipulator

Nominal Plant Model

•

Conventional Feedback Control

Design

•

µ-Synthesis Feedback Control Design

•

Experimental Evaluation

15.5 Conclusions

15.1 Introduction

This chapter deals with the robot motion control problem, whose objective is accurate execution of a

reference robot trajectory. This trajectory is executed by the robot end-effector in the operational space,

i.e., in the space where the robot performs its motion tasks. The dimension of this space is not higher than

six, as unique positioning and orientation of the end-effector require at most three Cartesian and three

angular coordinates. A desired operational trajectory is realized by controlling the motions in the robot

joints. The operational reference is mapped into the joint reference trajectory via the inverse kinematics

mapping [1,2]. The joint reference is realized by the joint servo control loops. Better quality of motion

control in the joint space contributes to higher motion performance in the operational space.

There are a number of criteria to evaluate the performance of motion control. A few will be listed here.

Accuracy of tracking a motion reference is the usual performance criterion. Intuitively, it is expected that if

the joint reference is realized with a higher accuracy, then the operationalmotion should be accurate as well.

However, the relation between accuracies in the joint and operational spaces is not as straightforward as

the previous sentence implies. The mapping from the joint to the operational motion (forward kinematics

[1,2]) is intrinsically nonlinear, and hence the accuracies of tracking these two motions are nonlinearly

related. Apart from joint conﬁguration, ﬂexibilities and disturbances may inﬂuence position of the robot

end-effector. In the presence of these effects, even highly accurate execution of the joint reference may give

unsatisfactory accuracy in the operational space. Therefore, these effects must be taken into account in the

motion control design.

-2 Robotics and Automation Handbook

The control bandwidth is another performance criterion. Although often addressed in manipulator

motion control, there is no unique deﬁnition of it. In [3] it is formulated as a range of frequencies contained

in the control input. A higher bandwidth should imply the potential of a manipulator control system to

realize faster motions, together with the possibility to compensate for dynamic effects and disturbances of

broader frequency content. If dynamics in the manipulator joints are linear and linear feedback control

strategies are used, then one may resort to conventional deﬁnitions of the control bandwidth [4]. Linear

dynamics can be realized by decoupling the robot axes either using high-gear transmission mechanisms

between the joint actuators and the robot links or by some nonlinear control compensation. The control

bandwidth in a given robot joint can be formulated as the cross-over frequency, i.e., the ﬁrst zero-crossing

of the open-loop gain of the servo-loop in this joint. Because of linearity, a higher bandwidth implies a

higher open-loop gain, which contributes to better motion accuracy.

Imposing a high feedback gain for the sake of better tracking accuracy is unacceptable if it also excites

parasitic dynamics(ﬂexibilities) and/or ampliﬁes disturbances (e.g.,measurement noise). Therefore,a level

of rejection of the parasitics and disturbances can be adopted as additional control performance criterion.

Stability and robustness issues are naturally important in robot motion control. Stabilization of robot

motions is achieved with a feedback control component. Motion control is robustly stable if despite uncer-

tainty in the robot dynamics and disturbances, the stability is preserved. There are two kinds of uncertain-

ties. The ﬁrst ones are parametric, and they arise if physical values of robot inertial and/or friction parame-

ters are not known exactly. The second ones are unmodelled dynamic effects, e.g., ﬂexibilities and friction.

As examples of disturbances, one may think of cogging forces and quantization noise. The former are typ-

ical for direct-drive manipulators [5], while the latter arises if incremental encoders are used as position

sensors. Better stability margins enhance robustness of motion control, because they guarantee the safe op-

eration despite uncertainties and disturbances. With linear decoupled joint dynamics and linear feedback,

control solutions, standard gain, and phase margins [4] can be considered as control performance criteria.

Increasing demands on the performance and robustness of manipulator motion control has led to the

development of versatile motion control approaches. Robust control strategies are introduced to stabilize

manipulator motions under uncertainty and disturbance conditions. More advanced strategies should

ensure that the desired performance of motion control is preserved despite uncertainties and disturbances.

This property is referred to as robust performance.

Decentralized PID (proportional, integral, derivative) and its variants PD and PI are conventional

feedback control solutions. The majority of industrial robot manipulators are equipped with high-gear

transmission mechanisms, so they can be describedby linear and decoupleddynamics. Linear conventional

controllers are suitable for such dynamics. They are appealing because of their efﬁciency in tuning and

low computational costs. However, if high-quality motion control performance is needed, conventional

controllers may lead to unsatisfactory results. Use of these controllers means making serious tradeoffs

among feasible static accuracy, system stability, and damping of high-frequency disturbances. For example,

smaller proportional action gives larger gain and phase margins for system stability, sacriﬁcing static

accuracy. A higher proportional gain improves static accuracy, but also ampliﬁes quantization noise

and other high-frequency disturbances. Inclusion of integral action improves static accuracy, but often

reduces stability margins. It is shown in [6] that these tradeoffs become critically conﬂicting with a

digital implementation of the control law, as the sampling rate decreases. The simplicity of conventional

controllerscan be toorestrictiveto provide compensation of each dynamic effect encounteredin the robotic

system: dynamic couplings between the joints, friction, backlash, ﬂexibility, and time-delay. Usually, the

conventional controllers can handle only a limited number of these effects, together with other control

objectives, e.g., prescribed control bandwidth and reduction of the position error. As non-compensated

effects may strongly inﬂuence motion performance, more sophisticated control strategies are needed. The

situation becomes even more critical if no transmission elements are present between joint actuators and

links, which is typical for direct-drive robots. Then, the nonlinear dynamic couplings directly apply upon

each joint actuator and their compensation requires use of more advanced control schemes.

Advanced manipulator control methods are capable of simultaneously realizing several control objec-

tives: stability robustness, disturbance rejection, controlled transient behavior, optimal performance, etc.

Motion Control by Linear Feedback Methods 15

-3

Of course, it is not possible to achieve arbitrary quality with each control objective independently, because

they are mutually dependent and are often conﬂicting. A detailed survey of advanced control methods

is available in [7]. Nonlinear representatives, such as adaptive and sliding-mode methods, can improve

system performance in the presence of uncertainty in the robot dynamics and external disturbances (e.g.,

variable load). The non-linearity of these methods, however, does not facilitate a quantitative prediction of

system performance for a given robustness level. This is a limiting factor for their widespread application

in practice, where it is often very important to know in advance worst-case motion accuracy for a given

bandwidth of reference trajectories.

Stability robustness, disturbance rejection, and controlled transient response can be jointly and directly

imposedusing feedbackschemes based on H

∝

controltheory.These schemesenable quantitativeprediction

of motion performance, given bounds on modeling uncertainty and disturbances. Moreover, with the

available knowledge of the system dynamics, parasitic effects, and disturbances, motion performance can

be optimized. These are the reasons that make H

∝

controllers appealing solutions for practical problems

and motivate their application in robotic systems.

Industrial practice teaches us that ultimate limits of performance and robustness of motion control

can be achieved only if all peculiarities of a controlled plant are taken into account during the control

design [8]. To illustrate practical effects of such reasoning, in this chapter we will present a detailed motion

control design applied to a direct-drive robotic manipulator with revolute joints. The dynamic behavior

of such a manipulator is highly nonlinear [5], which particularly impedes robust high-performance con-

trol. Undesirable effects, such as ﬂexibility, time-delay, and measurement noise, affect the manipulator

operation. As a remedy, we carry out a control design that relies on a comprehensive model of the rigid

manipulator dynamics and takes into account experimental characteristics of the manipulator. This design

consists of the following steps: (i) compensation of the manipulator dynamics via feedback linearization,

(ii) identiﬁcation and modeling of remaining (ﬂexible) dynamics, (iii) design of feedback controllers for

the identiﬁed dynamics to meet performance and robustness speciﬁcations, and (iv) evaluation of the

design.

The theory behind the control design will be formulated for the general case of a robotic manipulator

with n degrees of freedom. In the case study, the practical demonstration of the design will be given for a

direct-drive robotic manipulator. This demonstration should emphasize the feedback control tuning part.

The considered manipulator has three rotational joints, implemented as waist, shoulder, and elbow [9,10].

As a similar kinematic structure is often met in industry, results obtained for the case study should be

relevant for industrial cases. In the case study, the control design will effectively handle several objectives.

Namely, it will robustly preserve a speciﬁed accuracy of trajectory tracking, despite vibrations at the

robot base, high-frequency ﬂexible effects, time-delay, and measurement noise. The achieved accuracy

and bandwidth of motion control will be higher than feasible with conventional feedback design.

The chapter is organized as follows. Decentralized conventional feedback control will be considered in

Section 15.2. Use of a dynamic model in the motion control design and feedback control designs applied

with nonlinear model-based dynamic compensation will be presented in Section 15.3. Section 15.4 is the

case study. Conclusions will come at the end.

15.2 Decentralized Conventional Feedback Control

Let us represent the rigid-body dynamics of a robot manipulator with n joints using Euler-Lagrange’s

equations of motion[1,2,11]:

M(q(t))

q(t) + Q(q(t),

q(t))

q(t) + g(q(t)) +τ

(t) = τ (t) (15.1)

whereτ is the (n×1) vector of generalized forces acting at joints (torques for rotational joints and forces for

prismatic joints); q,

q and

q are the (n ×1) vectors of joint generalized motions, speeds, and accelerations,

respectively; M is the (n × n) inertia matrix; Q(q(t),

q(t))

q(t); g(q(t)), and τ

(t) are the (n ×1) vector

of Coriolis/centripetal, gravity, and friction effects, respectively, and t denotes time.

-4 Robotics and Automation Handbook

The dynamics (15.1) are highly nonlinear and coupled. Use of transmission elements between the joint

actuators and robot links can have linearizing effect on these dynamics [2]. Let θ and τ

denote the

(n ×1) vectors of actuator displacements and actuator driving torques, respectively; the transmissions

then establish the following relationships:

θ(t) = Nq(t)

(t) = N

−1

τ (t) (15.2)

where N is a diagonal matrix containing the gear reduction ratios n

. If the moments of inertia J

m,i

of each

actuator shaft are collected in the diagonal matrix J

, then the inertia matrix M can be split as follows:

M(q(t)) = NJ

N + M(q(t))

(15.3)

where NJ

N is the constant matrix, and M is the conﬁguration dependent matrix. Substituting Equa-

tion (15.2) and Equation (15.3) into Equation (15.1) yields:

(t) = J

θ(t) + d(t)

(15.4)

where

d(t) = N

−1

M(q(t))N

−1

θ(t) + N

−1

Q(q(t),

q(t))

θ(t)N

−1

+ N

−1

(g(q(t)) + τ

(t)) (15.5)

represents the nonlinear dynamic interaction between joint actuators. In case of high reduction ratios

1), thecontributionof the interactionissmall comparedwith the lineardynamics J

θ.Consequently,

the manipulator dynamics (15.4) are practically decoupled and linearized, as each component of τ

dominantly inﬂuences the corresponding component of θ, while d just plays the role of a disturbance for

each joint servo.

Control of the decoupled dynamics (15.4) can be done using a decentralized feedback method. Denote

with θ

(t) a reference trajectory of the actuator shaft, which is determined from the joint reference q

(t)via

Equation (15.2). Deﬁne the position error as the difference between the actual and the reference motion:

(t) = θ(t) − θ

(t) (15.6)

A decentralized control treats each robot joint as a separate plant to be controlled and applies decoupled

linear feedback control actions u

(i = 1, ..., n

) as follows:

(s) = J

(s)u(s ) (15.7)

where G

(s) = diag[G

a,1

(s), ..., G

a,n

(s)] is a diagonal matrix containing the actuator dynamics, u is the

(n ×1) vector of the feedback control actions, and s is the Laplace operator. Each u

is decoupled from

the remaining ones as it is based just on the position error θ

corresponding to the actuator i.

For convenience, we may assume no actuator dynamics (G

is identity) and a conventional PD feedback

control law with acceleration feedforward:

u(t) =

(t) − K

(t) (15.8)

whereK

=diag[k

p,1

, ..., k

p,n

] and K

=diag[k

d,1

, ..., k

d,n

] are matricesof positiveposition and velocity

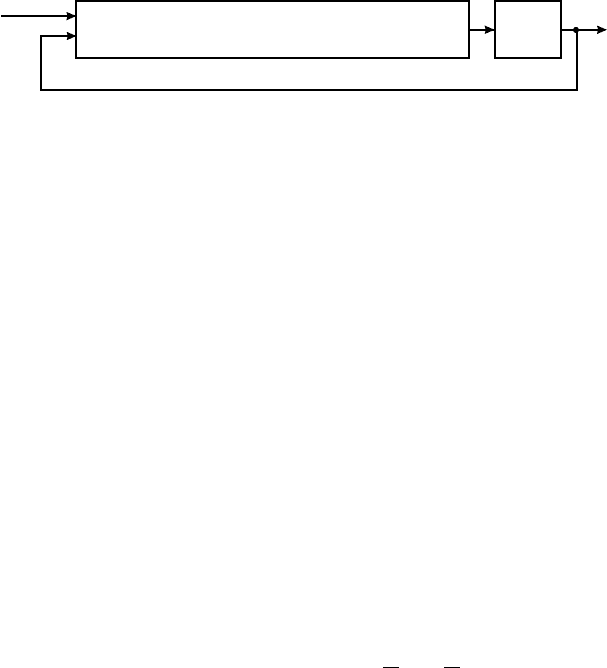
gains, respectively. The decentralized control approach of (15.7) and (15.8) is illustrated in Figure 15.1.

Robot

q, q

, q

...

, p

p, p

− K

(p − p

) − K

(p − p

)]

FIGURE 15.1 Decentralized motion control with PD feedback and acceleration feedforward.

Motion Control by Linear Feedback Methods 15

-5

The application of the control law (15.7) and (15.8) to the system (15.4) gives the error dynamics:

(

(t) + K

(t)) =−d(t) (15.9)

It follows that the position error falls into a region of size proportional to the magnitude of d(t). If this

region is narrow, which is the case when high reduction ratios are used, then the error can be made small

by appropriate selection of the PD gains. If the gear reduction ratios are small, or if N is the identity matrix

(direct-drive actuation), then the nonlinear coupling terms become more competitive or even dominant

for fast motions in comparison with the linear part in Equation (15.9). Consequently, the magnitude of

d(t) is not small, and position errors become larger for the same feedback controller gains. As a remedy,

one can apply a model-based compensation for d(t), which is explained in the next section.

15.3 Linear Feedback Control Applied with Nonlinear

Model-Based Dynamic Compensators

Nonlinear dynamic couplings between robot joints can be compensated using control algorithms that are

based on the knowledge of the dynamic model (15.1). The manipulator dynamics that are not covered with

the model are handled by a feedback control action. There are two common approaches to model-based

dynamic compensation [2,3,12]:

computed-torque control

M(q(t))

q(t) + Q(q(t),

q(t))

q(t) + g(q(t)) +τ

(t) + u(t) = τ (t)

(15.10)

feedback linearization

M(q(t))u(t) + Q(q(t),

q(t))

q(t) + g(q(t)) +τ

(t) = τ (t) (15.11)

In both approaches u(t) stands for the linear feedback control action, based on the error between the

actual and the reference joint motions:

e(t) = q(t) − q

(t) (15.12)

possibly extended with acceleration feedforward term. The role of u is to stabilize the manipulator motion

and ensure the desired performance when realizing the reference q

(t).

The laws (15.10) and (15.11) are often characterised as “centralized control,” because each component of

the control inputs τ contains dynamic interaction between the robot joints. The model-based terms given

in (15.10) and (15.11) are computed along the actual joint motions, speeds, and accelerations. However,

the reference motions and their time derivatives can also be used for their computation. Some feedback

designs applicable in the control laws (15.10) and (15.11) are presented next.

15.3.1 Computed-Torque Control Design

Assuming perfect model-based compensation of nonlinear dynamics including friction, a control law that

guarantees global uniform asymptotic stability of the origin (e,

e) = (0, 0) is given by [13]

M(q(t))

(t) + Q(q(t),

q(t))

(t) + g(q(t)) +τ

(t) − K

e(t) − K

e(t) = τ (t)

(15.13)

Here, K

= diag[k

p,1

, ..., k

p,n

] and K

= diag[k

d,1

, ..., k

d,n

] are matrices of positive position and

velocity gains, respectively. Obviously, the model-based terms employ both the reference and the actual

-6 Robotics and Automation Handbook

Robot

q, q

, q

M(q)q

+ Q(q, q)q

+ g(q) + s

− K

(q − q

) − K

(q − q

)

FIGURE 15.2 Computed-torque motion control with PD feedback.

joint trajectory. The control law (15.13), illustrated in Figure 15.2, achieves a passive mapping from the

error dynamics

M(q(t))

e(t) + Q(q(t),

q(t))

e(t) − K

e(t) = Ψ(t)

(15.14)

to the time derivative of the position error

e(t). This was proven in [13].

Although globally stabilizable and yielding better control performance than a decentralized controller,

it is not obvious how to tune the PD gains in (15.13) to realize the desired performance speciﬁcations, e.g.,

prescribed error reduction, bandwidth constraint, and attenuation of undesired high-frequency effects

(e.g., quantization noise and ﬂexibilities). The feedback tuning is performed by trial and error on the real

system,until a satisfactory trade-off amongstability, amount of error reduction, and impact of disturbances

is reached.

15.3.2 Control Designs with Feedback Linearization

The feedback linearization approach can establish a situation where common engineering reasoning can

be used for tuning the feedback control action. When applied, the control law (15.11) reduces the motion

control problem to the linear case, deﬁned in the Laplace domain:

q(s) = P(s )u(s), P(s ) = diag



, ...,



(15.15)

The dynamics from the feedback action u

to the displacement q

describe the plant P

to be controlled.

The plant deﬁned by (15.15) has perfectly rigid dynamics. Its frequency response function (FRF) has a

linear amplitude plot with –2 slope and constant phase at –180

◦

. Such an FRF can be established only if

the law (15.11) perfectly matches the real robot dynamics. In practice, this rarely happens, as no robot is

perfect in its realization, and hence, the rigid-body model used in (15.11) is hardly an accurate description

of the real robot dynamics. Instead of (15.15), one should rather consider control of a more general transfer

matrix P:

q(s) = P(s )u(s), P(s ) =







1,1

(s) ··· P

1,n

(s)

n,1

(s) ··· P

n,n

(s)







(15.16)

The transfer functions on the main diagonal of P represent dynamics between the feedback control

action at each robot joint and the displacement of that joint. The cross-terms represent interactions

between the joints that remain after imperfect compensation of the real robot dynamics. If any of these

cross-terms is not negligible when compared with the transfer functions on the main diagonal, we can

conclude that the dynamic model used in the feedback linearization is not sufﬁciently accurate. The

inclusion of the cross-terms does not principally limit the feedback design procedure, although it makes it

more involved. If the cross-terms are quantitatively smaller than the diagonal elements, then the transfer

matrix P can be considered as diagonal. This implies total decoupling of the robot dynamics (15.1) via

(15.11), which simpliﬁes the feedback control design to n single-input, single-output cases. When dealing

Motion Control by Linear Feedback Methods 15

-7

with practical problems, the diagonality of P must be analysed before proceeding to the feedback control

design.

Each feedback design is focused on a particular transfer function P

i,i

(s)(i = 1, ..., n), representing a

plant to be controlled. For convenience, the indices in the subscript will be replaced with a single one: the

plant for the ith joint will be denoted with P

(s). It is not a mere double integrator, as by virtue of (15.15)

one would expect, but a higher-order dynamical system with resonance and antiresonance frequencies

that emerge because of ﬂexibilities. A time delay can also be experienced in the plant dynamics. These

dynamics change for various operating conditions, as resonance frequencies and their relative damping

vary with the manipulator conﬁguration.

A technique to identify dynamics of the plant, i.e., FRF G

( j ω)(ω is angular frequency), is explained in

the chapter on modeling and identiﬁcation. Brieﬂy, this technique is based on analysis of spectra of input

and output signals measured under closed-loop conditions. For joint i, several FRFs are identiﬁed, each

corresponding to a different conﬁguration of the remaining joints. Denote the number of the identiﬁed

FRFs with N

, i.e., k = 1, ..., N

. For the feedback control design, it is preferable to determine one nominal

FRF, for which a parametric model of the plant P

could be devised. A natural choice for the nominal FRF

is some average of all identiﬁed FRFs. Such a choice minimizes the difference between the plant model

and the identiﬁed FRFs, which represents uncertainty in the plant dynamics. For example, one may use

the following averages to determine the nominal FRF:

( j ω) = arg min

( j ω)

max



( j ω) − G

( j ω)



or (15.17a)

( j ω) =



k=1

( j ω) (15.17b)

For each ω, the solution (15.17a) minimizes the distance in the complex plane between the nominal

FRF G

( j ω) and all G

( j ω), k = 1, ..., N

. The solution (15.17b) is an average of all identiﬁed FRFs. A

choice between (15.17a) and (15.17b) can be case dependent, although, in principle, the latter one gives

smoother magnitude and phase FRF plots.

The nominal G

( j ω) represents the plant dynamics as a set of data points. For a parametric description

of the nominal plant model P

, any technique of ﬁtting the parametric transfer function P

( j ω) into the

nominal data G

( j ω) can be used. A least-squares ﬁt using an output error model structure [14] is one

possibility. Once a parametric nominal plant model is available, it can be used in the feedback control

design.

The servosystem for joint i is depicted in Figure 15.3. Here, P

presents actual plant dynamics that

accounts for all variations from the nominal plant model P

. The objective of the feedback control design

is to determine the controller C

which realizes accurate tracking of the reference motion q

r,i

(t). To enhance

the performance of motion control, the known acceleration

r,i

(t) is used as the feedforward control input.

There are several options for the design of the feedback controller C

: LQ, LQG, loop-shaping, etc. In this

chapter the loop-shaping approach is explained in more detail, because it enables speciﬁcation of the

performance objectives and feedback tuning in a very intuitive way. LQG theory will be used for state

reconstruction in the case-study.

∗

−

FIGURE 15.3 Servo control system for joint i.

-8 Robotics and Automation Handbook

The objective of loop-shaping is to design a feedback controller which enforces the desired shape of the

closed-loop transfer functions for the servo-system shown in Figure 15.3. Standard transfer functions are

considered:

Sensitivity function S

= 1/(1 + L

)

Input sensitivity function U

= C

Complementary sensitivity function T

= 1 − S

where L

= P

is the open-loop gain of the servo-loop. Key is to use the open-loop as the primary loop

to shape, i.e., closed-loop speciﬁcations are transformed in a desired shape of the open-loop gain L

.From

the desired shape of L

, the required C

follows directly given the knowledge of the plant P

. The shaping

is performed according to standard rules [8]:

r.1 Stabilize the plant P

r.2 Ensure high open-loop gain L

within the largest possible cross-over frequency

r.3 Allow maximum peaking in the sensitivity function S

of 6 dB

r.4 Minimizeinﬂuenceofunmodelleddynamicsanddisturbancesonthe motion controlperformance

The simplest case is the use of the loop-shaping technique for tuning the k

p,i

and k

d,i

gains of the

conventional PD feedback controller:

(t) =

r,i

(t) + u

∗

(t) (15.18a)

∗

(t) =−k

p,i

(t) − k

d,i

(t) (15.18b)

wheree

is the ith element of the position error deﬁned by (15.12). Moreadvanceduse of loop-shaping is the

design of a feedback controller by custom selection of the shaping ﬁlters, e.g., lead/lag, notch, low-pass, etc.

Such a design can be found in [15]. Finally, an optimal loop-shaping design provides a feedback controller

minimizing the H

or H

∝

norm of a matrix based on the weighted closed-form transfer functions given

above. The weightings are frequency-dependent ﬁlters, suitably selected to enforce the desired performance

speciﬁcations. The availability of varioussoftware packages that enable calculation of the optimal controller

facilitates an optimal loop-shaping design. For illustration, two such designs will be sketched next.

The ﬁrst control design was presented in [16], and it aims at shaping the sensitivity and input sensitivity

functions.Ituses twofrequencydependent weighting functions W

and W

(i =1, ..., n)for performance

speciﬁcation in each servo system. Constraining the sensitivity function enforces a desired low-frequency

behavior in the closed loop:

( j ω)

≤ 1/



( j ω)



, ∀ω ∈ IR

(i = 1, ..., n) (15.19)

where ω denotes angular frequency deﬁnedonIR

={ x ∈IR |x ≥0}. By shaping the sensitivity, one may

impose a minimum bandwidth requirement and integral control. Attenuation of resonances at low fre-

quencies can be enforced, as well. Bounding the input sensitivity enforces the high-frequency roll-off,

which is important for robustness against high-frequency resonances and measurement noise:

( j ω)

≤ 1/



( j ω)



, ∀ω ∈ IR

(i = 1, ..., n)

(15.20)

The conditions (15.19) and (15.20) jointly hold if the cost function



sup

ω∈R





( j ω)S

( j ω)



( j ω)U

( j ω)





(i = 1, ..., n) (15.21)

is less than 1. Thus, the optimal loop-shaping procedure seeks for a controller C

which stabilizes the

servo-loop shown in Figure 15.3 and minimizes the given cost function, ensuring the minimum is below 1.

This optimization problem is known as the mixed-sensitivity problem [17]. It can be solved, for example,

using software routines presented in [18].

If needed, both W

and W

can be tuned to enforce compensation of parasitic and disturbance effects

observed in the controlled system. This is done through disturbance-based control design cycles [8],

according to the following algorithm:

Motion Control by Linear Feedback Methods 15

-9

1. A conventional PD feedback controller is used to stabilize the manipulator in the initial design cycle;

the manipulator is moving along trajectories spanning the whole conﬁguration space; the position

error(15.12) is measured and accumulated,and cumulative power spectra (CPSs — cumulativesums

of all components of the auto-power spectrum) of all error components are calculated; frequencies

above the bandwidth of the joint references at which the CPSs have steeper slopes reveal disturbance

effects (noise, cogging force, vibrations), which should be tackled with the feedback.

2. The weightings W

and W

are deﬁned to account for the observed disturbances.

3. Optimal controllers C

minimizing (15.21) for i = 1, ..., n are computed and implemented on

the manipulator to realize the reference trajectory in the new design cycle.

4. CPSs of newly measured position errors are calculated and evaluated; if the design speciﬁcations

have not been met yet, weightings W

and W

are adjusted.

5. The steps 3 and 4 are repeated until further improvement of the motion performance cannot be

achieved.

6. The latest determined C

(i = 1, ..., n) are adopted as the feedback controllers.

The second control design computes the feedback controllers via µ-synthesis [19]. Its objectives are

robust stability and robust performance of the servo-loop shown in Figure 15.3. Assume that a nominal

parametric model P

of the plant (joint) dynamics is available. The nominal model and actual plant

dynamics can be related using a multiplicative plant perturbation model:

(s) → P

(s)(1 + 

(s)) (15.22)

Here, 

(s) is the multiplicative uncertainty, representing the relative difference between P

and the

real dynamics. The uncertainty can be expanded as follows:



(s) = W

(s)δ

(s) (15.23)

where the stable parametric weighting function W

satisﬁes



( j ω)



≥



( j ω)

, ∀ω ∈ IR

(15.24)

to have the normalized scalar uncertainty

( j ω)

≤ 1, ∀ω ∈ IR

A bound for the uncertainty can be determined from the identiﬁed FRFs:



( j ω)

= max



( j ω) − P

( j ω)



, ∀ω ∈ IR

(k = 1, ..., N

) (15.25)

Any stable weighting function, preferably of low order, can be adopted for W

if its magnitude closely

bounds the perturbations



from above. According to the small gain theorem [19], the control of the

perturbed plant (15.22) is robustly stable if the following holds

( j ω)

< 1/



( j ω)



, ∀ω ∈ IR

(15.26)

Simultaneous speciﬁcation of the closed-loop objectives (15.19), (15.20), and (15.26) (shaping of S

, and T

) can be done using the block-diagram shown in Figure 15.4. In this block-diagram, the channel

−

FIGURE 15.4 Setup for servo design using µ-synthesis.