Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

-6 Robotics and Automation Handbook

friction regime. Because of the parameter v

s,i

, the model (14.12) cannot be represented linearly in all

friction parameters (v

s,i

, α

0,i

, α

1,i

, and α

2,i

). Thus, a joined regressor form of a robot dynamic model is

not possible with the model (14.12). This prevents simultaneous estimation of the friction parameters and

the BPS elements, using, for example, some time-efﬁcient least-squares technique.

Dynamic friction models aim at covering more versatile friction phenomena. Among others (see surveys

in [15,16]), the Dahl and the LuGre models are the most frequently cited, analysed, and implemented

dynamic models. They cover a number of static and dynamic friction phenomena and facilitate their

representation in a compact way. The LuGre model is more comprehensive than the Dahl one, and it has

the following form:

0,i

+ σ

1,i

+ α

2,i

= τ

− σ

0,i

γ (

)

(i = 1, ..., n)

(14.13)

where z

is a presliding deﬂection of materials in contact, γ (

)isdeﬁned by Equation (14.12), while σ

0,i

and σ

1,i

are the stiffness of presliding deﬂections and viscous damping of the deﬂections, respectively.

Notice that the static model (14.12) corresponds to the sliding behaviour (

= 0) of the LuGre model.

A drawback of the LuGre model is that for some choices of its coefﬁcients, the passivity condition from

speed

to friction force τ

is easily violated [18]. This condition reﬂects the dissipative nature of friction.

Without the passivity property, the LuGre model admits periodic solutions, which is not realistic friction

behavior. On the other hand, a linear parameterization of the LuGre model is obviously not possible, and

consequently, the joined regressor form of a dynamic model cannot be created.

A neural-network friction model is also used [19]



k=1

i,k

[1 −2/(exp(2w

i,k

) +1)] + α

2,i

= τ

(i = 1, ..., n) (14.14)

where f

i,k

, w

i,k

, and α

2,i

are unknown parameters. This static model can represent Stribeck, Coulomb,

and viscous effects, and it admits a straightforward online implementation. However, it cannot be linearly

parameterized, and consequently, the joined regressor form of a dynamic model is not possible with this

model.

When the robot model is completed, the next step is to obtain realistic values for the model parameters.

These parameters are acquired via estimation procedures, that are explained in the next section.

14.3 Estimation of Model Parameters

Anestimation of frictionparameterswillbe explained ﬁrst in this section. Friction parameters areestimated

separately from the BPS elements if the joined regressor form of a robot dynamic model cannot be created.

Then, brief descriptions of two methods for estimation of the BPS elements will be given.

14.3.1 Estimation of Friction Parameters

Unknown parameters of a friction model associated with the joint i can be collected in the vector p

Elements of this vector can be estimated on the basis of identiﬁcation experiments in open-loop. In

each experiment, the considered joint is driven with a sufﬁciently exciting control input τ

, and the

corresponding motion q

is measured. The remaining joints are kept locked by means of appropriate

hardware or by feedback control. In the latter case, the feedback controllers must be tuned such that the

motions in the remaining joints, possibly caused by the couplings effects and by gravity, are prevented.

The dynamics for joint i can be represented as



− τ





− c

sin q



(14.15)

Modeling and Identiﬁcation for Robot Motion Control 14

-7

where J

is the equivalent moment of inertia of the joint, and c

isacoefﬁcient of the gravity term. This

term vanishes if the axis of joint motion is parallel with the direction of gravity. The parameters J

and c

are usually not known exactly, so they need to be estimated together with the friction parameters.

An efﬁcient time-domain identiﬁcation procedure elaborated in [19] can be carried out to estimate

friction parameters of a static friction model together with J

and c

from Equation (14.15). This procedure

engages a recursive Extended Kalman ﬁltering technique for nonlinear continuous-time processes. The

procedure recursively updates estimates, until convergence of all unknown parameters is reached. Friction

parameters characteristic to the presliding friction regime of the LuGre model (14.13), i.e., σ

0,i

and σ

1,i

, can

be estimated using frequency response function (FRF) measurements, as explained in [20]. This procedure

requires an experiment where the considered joint is driven with a random excitation (noise) and the FRF

from the excitation τ

to the motion q

is measured. A low noise level is needed, so as to keep friction

within the presliding regime. Joint position sensors of high resolution are thus necessary, because very

small displacements have to be detected. The estimation procedure employs a linearization of (14.13)

around zero

, z

, and

,deﬁned in Laplace domain:

(s) =

(s)

+ (σ

1,i

+ α

2,i

)s + σ

0,i

+ c

(14.16)

The parameters α

2,i

and c

must be known beforehand. The transfer function (14.16) can be ﬁtted into

the measured FRF to determine the unknown σ

0,i

and σ

1,i

14.3.2 Estimation of BPS Elements

Assume that friction models associated with the robot joints reconstruct realistic friction phenomena

sufﬁciently accurately. If this is the case, then the friction component τ

is completely determined in a

robot rigid-body dynamic model (14.6), as well as in the corresponding regressor representation (14.10).

This facilitates estimation of the elements of the BPS set, using identiﬁcation experiments. During the

experiment the robot is controlled with decoupled PD (proportional, derivative) controllers to realize a

speciﬁc trajectory. This trajectory must be carefully chosen such that the corresponding control input

τ (t)sufﬁciently excites all system dynamics. If the applied τ (t) and the resulting q(t),

q(t), and

q(t)are

collected during the experiment, and postprocessed to determine elements of the BPS, then we speak about

batch estimation. If the estimation of the BPS is performed as the identiﬁcation experiment is going on,

then we speak about online estimation.

14.3.2.1 Batch LS Estimation of BPS

Assume ζ samples of each element of τ , q,

q, and

q have been collected. These samples correspond to time

instants t

, t

, ..., t

. By virtue of (14.10), we may form the following system of equations:

Φ · p = y

(14.17)

Φ =







R(q(t

q(t

))

R(q(t

q(t

))

R(q(t

q(t

))







(14.18)

y = [(τ (t

) −τ

))

,(τ (t

) −τ

))

, ...,(τ (t

) −τ

))

]

(14.19)

If the input τ (t)sufﬁciently excites the manipulator dynamics, then the LS (least-squares) estimate of

p is

p = Φ

y (14.20)

-8 Robotics and Automation Handbook

where # denotes a matrix pseudoinverse [21]. There are several criteria evaluating sufﬁciency of excitation.

The usual one is the condition number of Φ,deﬁned as the ratio between maximal and minimal singular

values of Φ. If this number is closer to 1, the excitation is considered better for a reliable estimation of p.In

[4] several other performance criteria are also listed, such as the largest singular value of Φ, the Frobenius

condition number of Φ, and the determinant of the weighted product between Φ and its transpose.

14.3.2.2 Online Gradient Estimator of BPS

Among several solutions for online estimation of the BPS elements [22], the gradient estimator is the

simplest choice. It resorts to the concept of prediction error. If an estimate

p of the BPS is available and the

friction component τ

is known, then the model (14.10) can be used to predict the difference between

the control input and friction:

R(q(t),

q(t),

q(t))

p =

τ (t) −τ

(t) =

(t)

(14.21)

The prediction error

is formed as the difference between

(t) and the measured τ

(t) = τ (t) −

(t):

(t) =

(t) − τ

(t)

= R(q,

p − R(q,

q)p

= R(q,

(14.22)

where

p =

p − p is the BPS estimation error. The following update law enables online estimation of the

BPS:

p =−αR

(q,

(14.23)

where α is a positive scalar estimation gain. In the given law, the unknown parameters are updated in the

converse direction of the gradient of the squared prediction error with respect to the parameters [22].

As in the batch LS estimation, the quality of the BPS estimates achieved with (14.23) strongly depends

on the choice of a trajectory the robot realizes during the identiﬁcation experiment. Design of such a

trajectory deserves special attention.

14.3.3 Design of Exciting Trajectory

The robot trajectory, which is realized during the identiﬁcation experiment, is called the exciting trajectory.

There are several designs of such a trajectory available in literature, and they are brieﬂy summarized in

[12]. A design suggested in [11] and [12] postulates the exciting trajectory as ﬁnite Fourier series with

predeﬁned fundamental frequency and with free coefﬁcients:

exc

(t) = q

0,i



j=1

j2πf

sin( j 2πft) −b

cos( j2πft)] (i = 1, ..., n) (14.24)

Here,  f [Hz] is the desired resolution of the frequency content, the number of harmonics N determines

the bandwidth of the trajectory, and the free coefﬁcients q

0,i

, a

, and b

(i = 1, ..., n; j = 1, ..., N)

should be determined such that all manipulator rigid-body dynamics are sufﬁciently excited during the

identiﬁcation experiment. The given exciting trajectory is periodic, which enables continuous repetition

of the identiﬁcation experiment and averaging of measured data to improve the signal-to-noise ratio.

Additional advantages are direct control of the resolution and of the bandwidth of the trajectory harmonic

content. The control of the bandwidth is an important precaution for avoiding frequency components

that excite the robot ﬂexible modes.

Modeling and Identiﬁcation for Robot Motion Control 14

-9

The exciting trajectory can be realized on the robotic systems using a PD feedback controller:

τ =−K

(q − q

exc

) −K

(

q −

exc

) (14.25)

whereK

=diag[k

p,1

, ..., k

p,n

] and K

=diag[k

d,1

, ..., k

d,n

] are matricesof positiveposition and velocity

gains, respectively. The applied τ sufﬁciently excites the system rigid-body dynamics if the free coefﬁcients

in (14.24) are determined by optimising some property of the information matrix Φ (e.g., the condition

number of Φ). No matter which property (performance criterion) is adopted, the resulting optimization

problem is nonconvex and nonlinear. Different initial conditions may lead to different exciting trajectories,

allcorrespondingto local minimaof theperformance criterion.Consequently,the optimization determines

a suboptimal, rather than the globally optimal exciting trajectory. Still, experience shows that use of

suboptimal trajectories gives satisfactory results.

The presence of disturbances in the collected q,

q, and

q affects the quality of the estimation methods

(14.20) and (14.23). The quality is better if disturbances are reduced to a minimum. High-frequency

quantization noise and vibrations caused by ﬂexibilities are disturbances commonly found in robot man-

pulators. By reconstruction of joint motions, speeds, and accelerations with carefully tuned Kalman ﬁlters

[9,10], a sufﬁcient rejection of the disturbances can be achieved.

14.3.4 Online Reconstruction of Joint Motions, Speeds, and Accelerations

Online reconstruction of q,

q, and

q using a Kalman ﬁlter will be formulated in discrete-time, assuming a

digital setup for data-acquisition from a robot joint. It is proven in [10] that at sufﬁciently high sampling

rates, usual in modern robotics, the discrete Kalman ﬁlter associated with the motion of a robot joint i can

be constructed assuming an all-integrator model for this motion. This model includes a correcting term

, representing the model uncertainty. It accounts for the difference between the adopted model and the

real joint dynamics. The correcting term is a realization of the white process noise ξ

, ﬁltered through a

linear, stable, all-pole transfer function. With the correcting term used, the reconstruction of q,

q, and

requires at least a third-order model.

As a case-study, we assume that ξ

is ﬁltered through just a single integrator. A continuous-time model

associated to the motion in the joint i has the form:

r,i

+ ν

= ξ

+ η

(14.26)

where

r,i

is the desired joint acceleration, and η

is the measurement noise. In the model (14.26), the joint

motion q

is regarded as the only measured coordinate. In the design of the Kalman ﬁlter the deviation

from the desired joint motion q

r,i

= q

−q

r,i

(14.27)

and its time derivative can be adopted as the states to be reconstructed, rather than the motion coordinates

themselves. In such a way, the state reconstruction process is merely for the deviation from the expected,

or modelled, trajectory [10]. Let T

denote themselves the sampling time used for both data-acquisition

and control. We may determine a discrete-time system involving identical solutions with the model that

arises after substituting Equation (14.26) into Equation (14.27) at t = kT

(k + 1) = E

(k) + g

)ξ

(k)

(k) = c

(k) +q

r,i

(k) + η

(k) (14.28)

-10 Robotics and Automation Handbook

where

(k) = [e

(k),

(k), ν

(k)]

(14.29a)







1 T

0.5T

01 T

00 1







, g







0.5T







(14.29b)

= [100]

(14.29c)

Here, k abbreviates kT

. A Kalman ﬁlter that optimally reconstructs the state x

in the presence of the

model uncertainty ν

and measurement noise η

has the form:

(k + 1) = E

)

(k)

(k) =

(k) + k

[

(k) −q

r,i

(k) − c

(k)] (14.30)

where

denotes updated state estimate and k

is a n ×1 vector of constant gains. As the ﬁlter reconstructs

deviations from the reference motions and speeds, together with the model uncertainty, the motion

coordinates can be reconstructed as follows:

r,i

(14.31)

To compute the vector k

, one needs covariances of the measurement noise η

and of the process noise

. Assuming white, zero mean quantization noise, uniformly distributed within a resolution increment

θ

of the position sensor, the straightforward choice for η

is θ

/12 (see [10] for details). The reference

[9] suggests a simple rule to choose ξ

: it should equal max

r,i

(maximum value of the square jerk of

the motion reference). In practice, these rules are used as initial choices, while the ﬁnal tuning is most

effectively done online. However, use of Bode plots from the measured e

to the reconstructed

— an

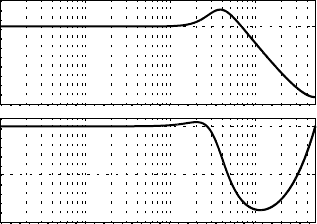
illustrative example is presented in Figure 14.2 — could be instructive for ﬁlter tuning. The Bode plots

reveal which harmonics of e

will be ampliﬁed after reconstruction, as well as which harmonics will be

attenuated. By analyzing the power spectrum of e

, a control engineer may locate spectral components

due to noise and other disturbing effects, that need to be ﬁltered out. The gain vector k

can be retuned to

reshape the Bode plot according to the needs.

−15

Magnitude (dB)

0.1

100

−60

−30

Frequency (Hz)

Phase (

)

FIGURE 14.2 Bode plots of the Kalman ﬁlter, from the measured e

to the reconstructed

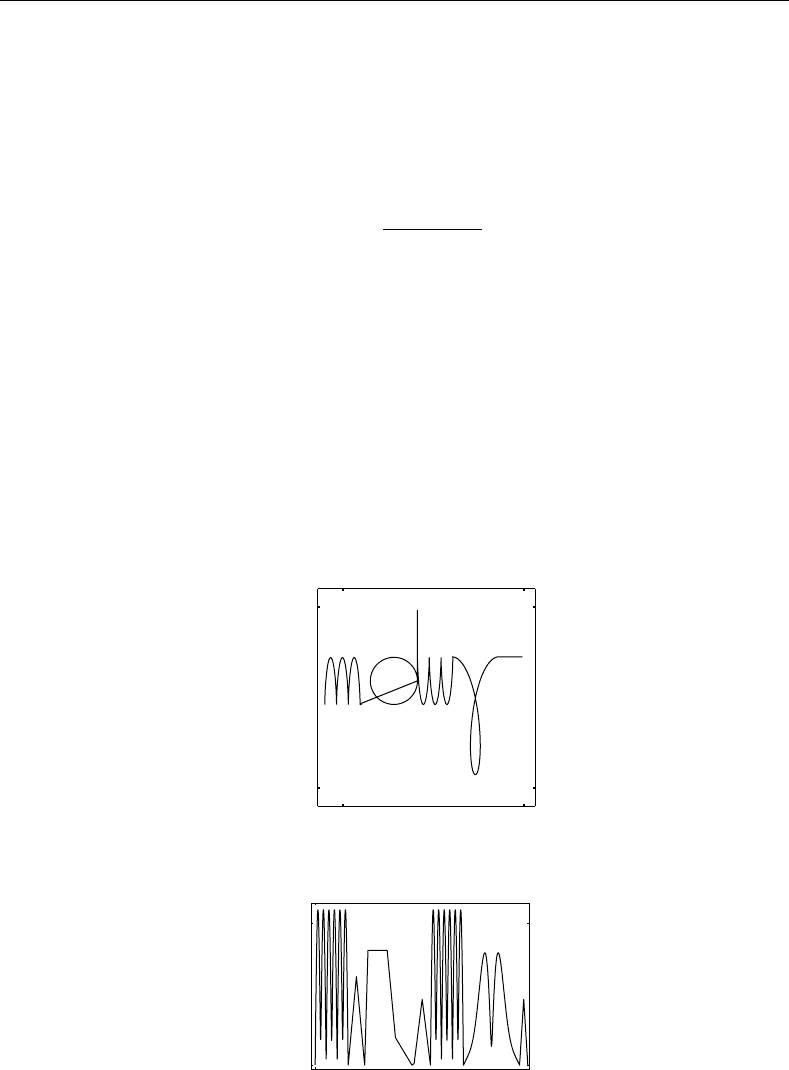
Modeling and Identiﬁcation for Robot Motion Control 14

-11

14.4 Model Validation

Writing and drawing tasks can be useful for model validation, because they require complex non-smooth

motions, and their execution may induce signiﬁcant dynamic forces/torques. An extensive study of human

handwriting is given in [13]. This reference considers one representative writing task: the sequence of letters

shown in Figure 14.3a. The given sequence is a concatenation of motion primitives typically executed by

robots. Mathematically, the sequence can be piecewise described in closed-form, with the possibility of

imposing an arbitrary velocity proﬁle. One may use this freedom to pose very demanding dynamic tasks,

that can be used for a rigorous veriﬁcation of robot kinematic and dynamic models.

For example, the robot-tip should realize the sequence of letters with the velocity proﬁle

v(t) =



(t) +

(t) (14.32)

presented in Figure 14.3b. The given proﬁle has fast and slow phases. Figure 14.3a and Figure 14.3b

deﬁne the reference trajectory of the robot-tip. An inverse kinematics model can be used to determine

the corresponding reference joint motions q

(t). Along these motions a dynamic model can be validated.

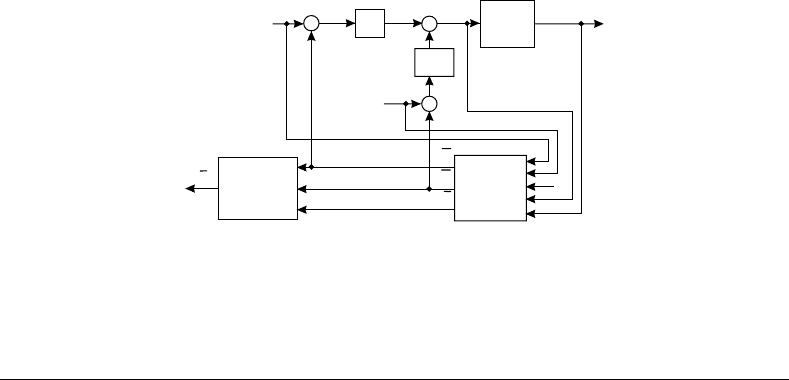
The organization of the validation experiment is illustrated in Figure 14.4. The objective is to test how

accurately the output

τ of the dynamic model, which is fed by online reconstructed joint motions, speeds,

and accelerations (see formulas (14.30) and (14.31)), reconstructs control signals generated with PD

controllers:

τ =−K

(

q − q

) −K

(

q −

) (14.33)

τ is close enough to τ , the dynamic model is considered appropriate for control purposes.

−0.25

0.25

0.35

0.85

(m)

(a)

0.7

Time (s)

Velocity (m/s)

(b)

FIGURE 14.3 Reference trajectory in the task space: (a) tip path, (b) adopted tip-velocity proﬁle.

-12 Robotics and Automation Handbook

Robot

Dynamic

model

Kalman

filter

−

FIGURE 14.4 Experimental validation of a robot dynamic model.

14.5 Identification of Dynamics Not Covered with a Rigid-Body

Dynamic Model

In model-based manipulator motion control, a dynamic model is used to compensate for the nonlinear

and coupled manipulator dynamics. To illustrate this, we may consider a motion control problem solved,

for example, using the feedback linearization [23]:

τ (t) = M(q(t))u(t) + c(q(t),

q(t)) + g(q(t)) +τ

(t)

(14.34)

Here, u(t) represents a feedback control action which should stabilize the manipulator motion and enforce

the desired accuracy in realizing a reference trajectory q

(t). The remaining variables are as in (14.6). When

applied, the control (14.34) should decouple the manipulator dynamics. The problem of controlling the

nonlinear-coupled system shifts to the problem of controlling the linear plants, deﬁned in the Laplace

domain:

(s) = q

(s)/u

(s)(i = 1, ..., n)

(14.35)

where u

is the ith component of u.

Ideally, the plant transfer function P

wouldbe modelled as a single mass (double integrator). The related

frequency response function (FRF) should have a linear amplitude plot with a –2 slope and constant phase

at –180

◦

. This holds if perfectly rigid-body dynamics are completely linearized by Equation (14.34). In

practice this may not happen, as a perfectly rigid mechanical construction is difﬁcult to achieve, and

hence, the rigid-body model is hardly an accurate description of the realistic manipulator dynamics.

Rather than a double integrator, P

has a more involved FRF, incorporating resonances and antiresonances

due to ﬂexibilities. The frequencies of these resonances and antiresonances may vary as the manipulator

changes its conﬁguration. The ﬂexible dynamics not covered with the rigid-body model inﬂuence feasible

performance and robustness in motion control. Therefore, it is worthwhile spending additional effort on

identifying these dynamics.

Inthe following we sketchtwo standardtechniquescapable of, at least, local identiﬁcation ofmanipulator

dynamics not covered with the rigid-body model. The ﬁrst technique is based on spectrum analysis, while

the second one is established in time-domain. Both of them utilize separate identiﬁcation experiments for

each joint (n experiments for the whole manipulator). Each experiment is performed under closed-loop

conditions, because the dynamics not covered with the rigid-body model might not be asymptotically

stable. For example, when identifying dynamics in joint i, this joint is feedback controlled to realize a slow

motion of a constant speed

r,i

, while the remaining ones take some static posture. A low constant speed

is preferable to reduce the inﬂuence of friction effects on the quality of identiﬁcation. The slow motion

is performed within the joint range. If, for example, the range in the revolute joint is not limited, a full

revolution can be made. The direction of movement is changed after reaching the joint limit, or after the

full revolution. Denote with q

(t)an(n × 1) vector of set-points, used in the identiﬁcation experiment.

Modeling and Identiﬁcation for Robot Motion Control 14

-13

Elements of q

(t) should satisfy

r,i

(t) =

r,i

and

r, j

(t) ≡ 0ifi = j . The speciﬁed set-points can be

achieved by applying the control law (14.34) with

u =−K

(q − q

) −K

(

q −

) +n (14.36)

where K

= diag[k

p,1

, ..., k

p,n

] and K

= diag[k

d,1

, ..., k

d,n

] are matrices of positive position and

velocity gains, respectively, and the (n × 1) vector n contains a random excitation (noise) as ith element

and zeroselsewhere. Identiﬁcationis more reliable if the inﬂuenceof disturbances (e.g., quantization noise)

affecting the manipulator motion and speed is low. For that purpose, M, c, g, and τ

in Equation (14.34)

can be computed along q

(t) and

(t).

The spectrum analysis technique identiﬁes an FRF of the plant dynamics P

( j ω) = q

( j ω)/u

( j ω),

where ω denotes angular frequency. A comprehensive description of techniques for FRF identiﬁcation is

available in [24]. If computed directly from the measured u

(t) and q

(t), the obtained FRF may appear

unreliable. We characterize an FRF as unreliable if the coherence function

 =



(14.37)

is small. 

and 

denote the autopower spectra of the excitation signal and of the joint response,

respectively, while 

is the cross power spectrum between the excitation and the response.  becomes

small if the excitation and response data are correlated, which is usual if these data are measured in closed-

loop. If this is the case, one should carry out indirect, instead of the direct identiﬁcation of the plant’s

FRF.

In the indirect identiﬁcation, an FRF of the transfer from n

(t)tou

(t) is estimated ﬁrst (n

is the ith

element of n in (14.36)). This estimation represents the sensitivity function S

( j ω) = [1 + ( jωk

d,i

p,i

( j ω)]

−1

for the feedback loop in the joint i. The coherence of this approach is normally sufﬁcient for

reliable estimation in the frequency range beyond the bandwidth of the closed-loop system in the joint i.

Hence, a low bandwidth for the closed-loop in the joint i is preferable. On the other hand, sufﬁciently high

bandwidths of the feedback loops in the remaining joints are needed to prevent any motion in these joints.

Therefore, separate sets of controller settings are required. With the identiﬁed sensitivity, for a known

setting of the PD gains, one may ﬁnd the plant’s FRF:

( j ω) =

1/S

( j ω) − 1

jωk

d,i

+ k

p,i

(14.38)

The obtained FRF represents dynamics of the joint i, which are not compensated with the rigid-body

dynamic model, as a set of data. For the control design it is more convenient to represent these dynamics

with some parametric model in a transfer function or state-space form. There are a number of solutions

to ﬁt a parametric model into FRF data [24]. The least-square ﬁt using an output error model structure

model is one possibility [25].

The time-domain technique directly determines a parametric model of the plant dynamics. Here, it is

only sketched for the case of direct identiﬁcation, which is based on the measured excitation u

(t) and

response q

(t) data. Extension to indirect identiﬁcation is straightforward. If collected at discrete time

instants t

, t

, ..., t

, the measurement pairs {u

), q

)}, {u

), q

)}, ..., {u

), q

)}can be used

for identiﬁcation of the plant dynamics assuming a transfer function model of the form

(z)

= P

(z) =

−1

+ b

−2

+···+b

−n

1 −a

−1

−···−a

−n

(14.39)

This model, deﬁned in Z-domain, is often referred to as the ARMA (autoregressive moving-average)

model [26]. Provided n <ζ, the least-squares estimates of the model coefﬁcients

ϑ = [a

...a

...b

]

(14.40)

-14 Robotics and Automation Handbook

can be determined using the formula

ϑ = F

(14.41)

where # denotes matrix pseudoinverse and







n+1

)

n+2

)







F =







) q

n−1

) ··· q

) u

) ··· u

)

n+1

) q

) ··· q

) u

n+1

) ··· u

)

ζ −1

) q

ζ −2

) ··· q

ζ −n+1

) u

ζ −1

) u

ζ −2

) u

ζ −n+1

)







(14.42)

The determined parametric model of the plant is used for design of a feedback controller. A more

realistic model contributes to higher performance of robot motion control and better robustness against

uncertainty in the manipulator dynamics. Experience shows that robust model-based motion control of

high performance is possible only if all notable peculiarities of the manipulator dynamics are recognized

and taken into account during the feedback control design. This certainly increases the time needed for

system identiﬁcation, control design, and feedback tuning. However, a beneﬁt from application of the

resulting controller is a robotic system of improved quality.

14.6 Case-Study: Modeling and Identification of a Direct-Drive

Robotic Manipulator

Practical application of the theoretical concepts presented so far will be illustrated for the case of a realistic

robotic manipulator of spatial kinematics and direct-drive actuation.

14.6.1 Experimental Set-Up

The robotic arm used for experimental identiﬁcation is shown in Figure 14.5. This experimental facility

is used for research on modeling, identiﬁcation, and control of robots [27–32]. Its three revolute joints

(n = 3 − RRR kinematics) are actuated by gearless brushless DC direct-drive motors. The joints have

inﬁnite range of motions, because power and sensor signals are transferred via sliprings. The coordinate

frames indicated in Figure 14.5 are assigned according to the DH convention. Numerical values of the DH

parameters are given in Table 14.1. The actuators are Dynaserv DM-series servos with nominal torques

of 60, 30, and 15 Nm. These servos are equipped with incremental optical encoders with a resolution of

∼10

−5

rad. Each actuator is driven by a power ampliﬁer, which ensures a linear proportionality between

the input voltage and the output motor torque. Both encoders and ampliﬁers are connected to a PC-based

TABLE 14.1 DH Parameters of the RRR

Robot

i α

[rad] a

[m] q

[m]

1 π/2 0 q

= 0.560

20P

= 0.200 q

= 0.169

30P

= 0.415 q

= 0.090

Modeling and Identiﬁcation for Robot Motion Control 14

-15

FIGURE 14.5 The RRR robot.

control system. This system consists of a MultiQ I/O board from Quanser Consulting (8 × 13 bits ADC,

8 ×12 bits DAC, eight digital I/O, six encoder inputs, and three hardware timers), combined with the soft

real-time system Wincon from Quanser Consulting. The control system facilitates online data acquisition

and control directly from Matlab/Simulink.

The rigid-bodydynamics has a dominant role in the overall dynamic behavior of the RRR robot. Friction

in the robot joints can be observed, too. Moreover, several effects not covered by the rigid-body dynamics

with friction can be excited, e.g., vibrations at the robot base and high frequency resonances. These effects

cannot be ignored if a high quality feedback control design is desired.

14.6.2 Kinematic and Dynamic Models in Closed Form

Kinematic and rigid-body dynamic models of the RRR robot were derived following the procedure ex-

plained in subsections 14.2.1 and 14.2.2. The models are available in closed form, which highly facilitates

their analysis and manipulation, as well as a model-based control design.

The elements of the matrix

, which maps orientation of the tip coordinate frame ‘3’ to the base

frame ‘0,’ are as follows:

1,1

= cos q

cos(q

), o

1,2

=−cos q

sin(q

), o

1,3

= sin q

, o

2,1

= sin q

cos(q

)

2,2

=−sin q

sin(q

), o

2,3

=−cos q

, o

3,1

= sin(q

), o

3,2

= cos(q

), o

3,3

= 0 (14.43)

The orthogonal projections of the vector

(q) pointing from the origin of ‘0’ to the origin of ‘3’ are

x = cos q

cos(q

) +a

cos q

) +(d

+ d

) sin q

y = sin q

cos(q

) +a

cos q

) − (d

+ d

)cosq

z = a

sin(q

) +a

sin q

+ d

(14.44)