Kurfess T.R. Robotics and Automation Handbook
Подождите немного. Документ загружается.


14
-16 Robotics and Automation Handbook
Equation (14.43) and Equation (14.44) define forward kinematics (FK) of the RRR robot. The inverse
kinematics (IK) is determined by solving the Equations (14.44) for q
1
, q
2
, and q
3
:
q
1
= asin
x(d
2
+ d
3
) + y
x
2
+ y
2
− (d
2
+ d
3
)
2
x
2
+ y
2
q
3
= atan
±
1 −
p
2
wh
+ p
2
wv
− a
2
2
− a
2
3
2
/(2a
2
a
3
)
2
p
2
wh
+ p
2
wv
− a
2
2
− a
2
3
/(2a
2
a
3
)
q
2
= atan
(a
2
+ a
3
cos q
3
)p
wv
− a
3
sin q
3
p
wh
(a
2
+ a
3
cos q
3
)p
wh
+ a
3
sin q
3
p
wv
p
wh
=
[x − (d
2
+ d
3
) sin q
1
]
2
+ [y + (d
2
+ d
3
)cosq
1
]
2
, p
wv
= z − d
1
(14.45)
The closed-form representation (14.45) has three advantages: (i) an explicit recognition of kinematic
singularities, (ii) a direct selection of the actual robot posture by specifying a sign in the expression for
q
3
, as the arm can reach each point in the Cartesian space either with the elbow up (− sign) or with
the elbow-down (+ sign), and (iii) a faster computation of a highly accurate IK solution than using any
recursive numerical method.
A rigid-body dynamic model of the RRR robot was initially derived in the standard form (14.6).
After that, for the sake of identification, it was transformed into regressor form (14.10). The number
of BPS elements is 15, coinciding with the number obtained using the formula derived in [14]. For a
given kinematics, this formula computes the minimum number of inertial parameters whose values can
determine the dynamic model uniquely. The elements of p and R are expressed in closed-form:
p
1
=a
2
2
m
3
+ a
2
m
2
(a
2
+ 2x
2
) − I
xx,2
+ I
yy,2
p
2
=−2(a
2
m
2
y
2
+ I
xy,2
)
p
3
= m
3
(a
3
+ x
3
)
p
4
= m
3
y
3
p
5
=a
3
m
3
(a
3
+ 2x
3
) − I
xx,3
+ I
yy,3
p
6
= 2(a
3
m
3
y
3
+ I
xy,3
)
p
7
= 2d
2
m
2
z
2
+ d
2
2
m
2
+ 2(d
2
+ d
3
)m
3
z
3
+ (d
2
+ d
3
)
2
m
3
+ I
yy,1
+ I
xx,2
+ I
xx,3
p
8
=−(d
2
+ d
3
)m
3
y
3
− I
yz,3
p
9
=−a
3
m
3
(z
3
+ d
2
+ d
3
) −(d
2
+ d
3
)m
3
x
3
− I
xz,3
p
10
=−d
2
m
2
y
2
− I
yz,2
p
11
=−a
2
[m
3
(z
3
+ d
2
+ d
3
) +m
2
(d
2
+ z
2
)] −d
2
m
2
x
2
− I
xz,2
p
12
=
a
2
2
+ a
2
3
+ 2a
3
x
3
m
3
+ a
2
m
2
(a
2
+ 2x
2
) + I
zz,2
+ I
zz,3
p
13
=a
3
m
3
(a
3
+ 2x
3
) + I
zz,3
p
14
= m
2
(x
2
+ a
2
) +m
3
a
2
p
15
= m
2
y
2
(14.46)
r
1,1
=
¨
q
1
cos
2
q
2
−
˙
q
1
˙
q
2
sin(2q
2
)
r
1,2
= 0.5
¨
q
1
sin(2q
2
) +
˙
q
1
˙
q
2
cos(2q
2
)
r
1,3
= 2a
2
{[
¨
q
1
cos(q
2
+q
3
) −
˙
q
1
˙
q
3
sin(q
2
+q
3
)] cos q
2
−
˙
q
1
˙
q
2
sin(2q
2
+q
3
)}
r
1,4
=−2a
2
[(
¨
q
1
sin(q
2
+q
3
) +
˙
q
1
˙
q
3
cos(q
2
+q
3
)) cos q
2
+
˙
q
1
˙
q
2
cos(2q
2
+q
3
)]
r
1,5
=
¨
q
1
cos
2
(q
2
+q
3
) −
˙
q
1
(
˙
q
2
+
˙
q
3
)sin(2q
2
+ 2q
3
)
r
1,6
=−0.5
¨
q
1
sin(2q
2
+ 2q
3
) −
˙
q
1
(
˙
q
2
+
˙
q
3
)cos(2q
2
+ 2q
3
)
r
1,7
=
¨
q
1
Copyright © 2005 by CRC Press LLC
Modeling and Identification for Robot Motion Control 14
-17
r
1,8
= (
¨
q
2
+
¨
q
3
) cos(q
2
+q
3
) −(
˙
q
2
+
˙
q
3
)
2
sin(q
2
+q
3
)
r
1,9
= (
¨
q
2
+
¨
q
3
) sin(q
2
+q
3
) +(
˙
q
2
+
˙
q
3
)
2
cos(q
2
+q
3
)
r
1,10
=−
˙
q
2
2
sin q
2
+
¨
q
2
cos q
2
r
1,11
=
˙
q
2
2
cos q
2
+
¨
q
2
sin q
2
r
2,1
= 0.5
˙
q
2
1
sin(2q
2
)
r
2,2
=−0.5
˙
q
2
1
cos(2q
2
)
r
2,3
= 2a
2
(
¨
q
2
+ 0.5
¨
q
3
)cosq
3
−
0.5
˙
q
2
3
+
˙
q
2
˙
q
3
sin q
3
+ 0.5
˙
q
2
1
sin(2q
2
+q
3
)
+ g · cos(q
2
+q
3
)
r
2,4
= 2a
2
− (
¨
q
2
+ 0.5
¨
q
3
) sin q
3
−
0.5
˙
q
2
3
+
˙
q
2
˙
q
3
cos q
3
+ 0.5
˙
q
2
1
cos(2q
2
+q
3
)
− g · sin(q
2
+q
3
)
r
2,5
= 0.5
˙
q
2
1
sin(2q
2
+ 2q
3
)
r
2,6
= 0.5
˙
q
2
1
cos(2q
2
+ 2q
3
)
r
2,8
=
¨
q
1
cos(q
2
+q
3
)
r
2,9
=
¨
q
1
sin(q
2
+q
3
)
r
2,10
=
¨
q
1
cos q
2
r
2,11
=
¨
q
1
sin q
2
r
2,12
=
¨
q
2
r
2,13
=
¨
q
3
r
2,14
= g · cos q
2
r
2,15
=−g · sin q
2
r
3,3
=a
2
0.5
˙
q
2
1
+
˙
q
2
2
sin q
3
+ cos q
3
¨
q
2
+ 0.5
˙
q
2
1
sin(2q
2
+q
3
)
+ g · cos(q
2
+q
3
)
r
3,4
=a
2
0.5
˙
q
2
1
+
˙
q
2
2
cos q
3
−
¨
q
2
sin q
3
+ 0.5
˙
q
2
1
cos(2q
2
+q
3
)
− g · sin(q
2
+q
3
)
r
3,5
= 0.5
˙
q
2
1
sin(2q
2
+ 2q
3
)
r
3,6
= 0.5
˙
q
2
1
cos(2q
2
+ 2q
3
)
r
3,8
=
¨
q
1
cos(q
2
+q
3
)
r
3,9
=
¨
q
1
sin(q
2
+q
3
)
r
3,13
=
¨
q
2
+
¨
q
3
r
1,12
=r
1,13
= r
1,14
= r
1,15
= r
2,7
= r
3,1
= r
3,2
= r
3,7
= r
3,10
= r
3,11
= r
3,12
= r
3,14
= r
3,15
= 0
(14.47)
Given expressions reveal the complexity of the nonlinear robot dynamics,enabling analysis of each dynamic
effect.Withthe elements of(14.47) containing the gravitational constant g , one mayassemble gravity terms;
with the elements containing joint accelerations, the inertial terms can be recovered, while the remaining
elements define Coriolis and centripetal terms.
14.6.3 Establishing Correctness of the Models
To establish correctness of the models (14.45)–(14.47), the writing task presented in Figure 14.3a and
Figure 14.3b can be considered. With the numerical values of the DH parameters given in Table 14.1,
the IK model (14.45) computes the joint motions, shown in Figure 14.6a. The equivalent joint speeds are
presentedin Figure14.6b.These plots revealnon-smooth joint motions, with significantspeed levels. These
motions are compared with the IK solution computed using a recursive numerical routine, implemented
in A Robotics Toolbox for Matlab [7]. The guaranteed accuracy of the recursive solution was better than
10
−10
rad. The differences between the IK solutions computed with the closed-form model (14.45) and
with the Robotics Toolbox are within the accuracy of the latter ones, see Figure 14.7. This verifies the
correctness of (14.45).
Copyright © 2005 by CRC Press LLC
14
-18 Robotics and Automation Handbook
0 10
−1.6
0
2.5
Time (s)
Angles (rad)
q
1
q
2
q
3
(a)
−1
0
1
−2
0
2
0 10
−1
0
1
Time (s)
q
2
(rad/s)
.
q
1
(rad/s)
.
.
q
3
(rad/s)
(b)
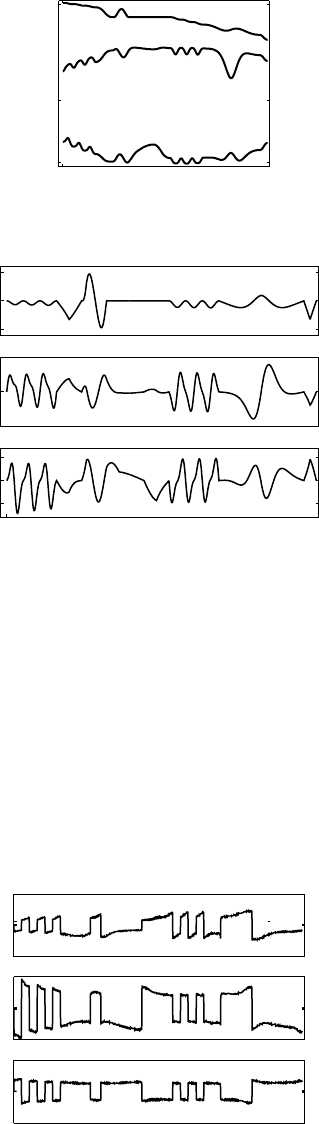
FIGURE 14.6 The joint space trajectory for the writing task: (a) motions, (b) speeds.
To establish the correctness of the rigid-body model (14.46) and (14.47), all inertial parameters are
assigned arbitrary nonzero values, positive for masses and principal moments of inertia, without sign
constraint for products of inertia and coordinates of centers of masses. The model computes torques corre-
spondingtothe jointspacetrajectoryshown in Figure14.6a and Figure14.6b.The torquesarealso calculated
using a recursive numerical routine implemented in the Robotics Toolbox. The differences between the two
−5
0
5
e
1
(rad)
−5
5
0
e
2
(rad)
0 10
−2
0
2
e
3
(rad)
Time (s)
×10
−12
×10
−12
×10
−11
FIGURE 14.7 Differences between the closed-form and the recursive IK solutions.
Copyright © 2005 by CRC Press LLC
Modeling and Identification for Robot Motion Control 14
-19
−1
0
1
e
1
(Nm)
e
2
(Nm)
e
3
(Nm)
−5
0
5
0 10
−2
0
2
Time (s)
×10
−14
×10
−15
×10
−15
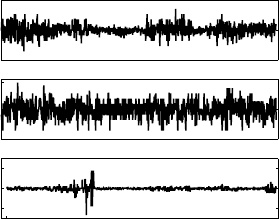
FIGURE 14.8 Differences in torques computed using the closed-form and recursive representations of the rigid-body
dynamic model.
solutions are caused by round-off errors only, see Figure 14.8. This verifies correctness of Equation (14.46)
and Equation (14.47).
14.6.4 Friction Modeling and Estimation
Two friction models are considered: the dynamic LuGre model (14.13) and the static neural-network
model (14.14). The parameters of the LuGre model v
s,i
, α
0,i
, α
1,i
, and α
2,i
(i = 1, 2, 3), which correspond
to the sliding friction regime, as well as the parameters of the neural-network model f
i,k
, w
i,k
, and α
2,i
(i = 1, 2, 3; k = 1, 2, 3), were estimated using a recursive Extended Kalman filtering method addressed
in subsection 14.3.1. The parameters of the LuGre model corresponding to the presliding regime were
estimated using the frequency-domain identification method, also mentioned in subsection 14.3.1. More
details about both identification methods can be found in [29] and [30]. Only one way for model validation
is presented here, for the neural-network model, because no essential improvement in representing friction
effects was observed using the LuGre model.
For illustration, the validation results for the third joint are given. For this validation, angular and speed
responses to the input torque τ
3
shown in Figure 14.9a were measured. The identical input was applied to
the model (14.14), whose parameters were assigned to the estimates. The model was integrated to compute
the corresponding joint motion and speed. The results are shown in Figure 14.9b with thin lines, while
thick lines represent the experimentally measured data. By inspection we observe high agreement between
experimental and simulated data, which validates the estimated friction model. Similar results hold for
the other joints of the RRR robot.
14.6.5 Estimation of the BPS
As explained in subsection 14.3.3, a reliable estimation of the elements of the BPS (14.46) requires custom
design of an exciting trajectory. This trajectory is executed in the identification experiment. Motions of
the exciting trajectory for the RRR robot were postulated as in (14.24). For frequency resolution we chose
f = 0.1 Hz, imposing a cycle period of 10 s. From an experimental study it was known that joint motions
within the bandwidth of 10 Hz do not excite flexible dynamics. Consequently, the number of harmonics
was selected as N = 100. The next step was computing the free coefficients q
0,i
, a
ij
, and b
ij
(i = 1, ..., n;
j = 1, ..., N) in (14.24), that minimize the condition number of the information matrix (14.18). This
matrix was created by vertical stacking the regression matrices, that correspond to discrete time instants
0, 0.1, 0.2, ..., 10 s. Elements of each regression matrix are given by (14.47), and they were computed
along the exciting trajectory (14.24). The free coefficients were found using a constrained optimization
Copyright © 2005 by CRC Press LLC
14
-20 Robotics and Automation Handbook
Time (s)
010
−2.5
0
2.5
Input torque (Nm)
(a)
−1
0
0.8
Angles (rad)
0 10
−4
0
4
Speeds (rad/s)
Time (s)
(b)
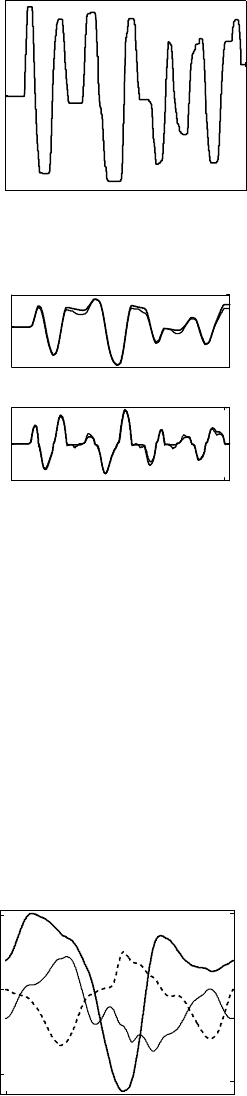
FIGURE 14.9 (a) Torque applied to the third joint for the friction model validation; (b) measured (thick) and
simulated (thin) angular motions and speeds in the third joint.
algorithm that takes care about constraints on permissible speed and acceleration ranges in the robot
joints: |
˙
q
1
|≤2π rad/s, |
˙
q
2
|≤3π rad/s, |
˙
q
3
|≤3π rad/s, and |
¨
q
i
|≤60 rad/s
2
(i = 1, 2, 3). The achieved
(suboptimal) condition number was 3.1. The determined coefficients were inserted into (14.24) to give
the motions shown in Figure 14.10.
The exciting trajectory was realized with the feedback controller (14.25), which used online recon-
structed joint motions and speeds as feedback coordinates. The reconstruction was done according to
the Equation (14.30) and Equation (14.31). The PD gains were tuned with “trial and error” to ensure
0 10
−5
0
4
Time (s)
Angles (rad)
FIGURE 14.10 Motions of the exciting trajectory: q
exc
1
—thick solid, q
exc
2
—thin solid, and q
exc
3
—dotted.
Copyright © 2005 by CRC Press LLC
Modeling and Identification for Robot Motion Control 14
-21
−40
0
55
−28
0
26
010
−6
0
9
Time (s)
τ
1
(Nm)τ
2
(Nm)τ
3
(Nm)
(a)
−9
0
12
−4
0
4
0
10
−2.5
0
4
Time (s)
τ
1
f
(Nm)τ
2
f
(Nm)τ
3
f
(Nm)
(b)
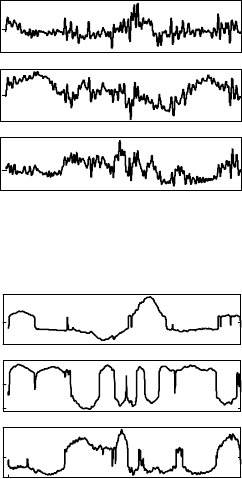
FIGURE 14.11 (a) Control inputs from the identification experiments; (b) reconstructed friction torques.
reasonable tracking of the exciting trajectory, with a low level of noise in the control inputs τ
i
(i = 1, 2, 3)
presented in Figure 14.11a. The sampling time was T
s
= 1 ms. Because the parameters of the friction
models (14.14) in all three joints had been estimated already, the friction torques τ
f
i
(t)(i = 1, 2, 3) were
reconstructed, too. These are shown in Figure 14.11b.
After collecting all the data used in Equation (14.18) and Equation (14.19), the batch LS estimation
(14.20) of the BPS elements could be carried out. To facilitate estimation, one may take advantage of the
symmetric mass distribution in the links 2 and 3, along the positive and negative directions of the axes
2
y
and
3
y, respectively (see Figure 14.5). These symmetries imply that y
2
and y
3
coordinates of the centres of
masses of the links 2 and 3 are identically zero. By virtue of Equation (14.46), it follows that the elements
p
4
and p
15
are also identically zero. This reduces the dimensionality of the problem, as instead of all 15
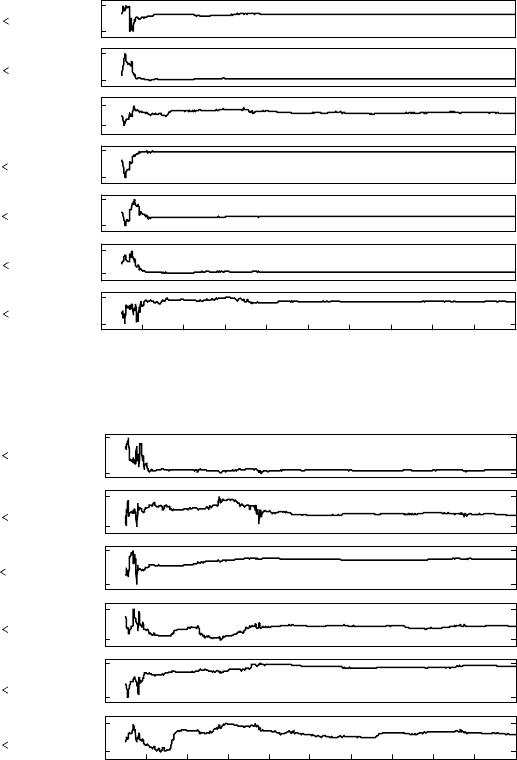
parameters, only 13 elementsof the BPS need estimation. As apparent fromthe plots shown in Figure 14.12,
the LS method results in the convergence of all 13 estimated elements of
ˆ
p.
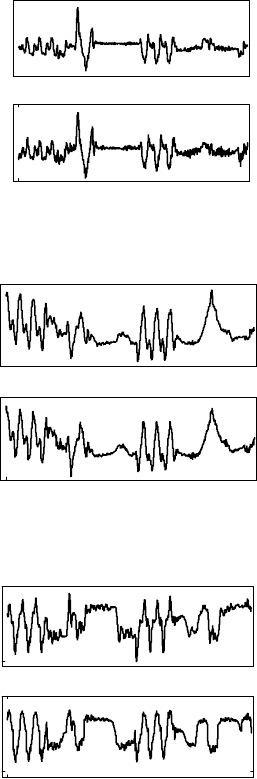
To evaluate the quality of the estimates, a validation experiment depicted in Figure 14.4 was performed.
The robot was realizing the writing task shown in Figure 14.3a and Figure 14.3b, with the joint motions and
speedspresentedin Figure14.6aand Figure 14.6b.The objectivewastocheckhowgood the estimatedmodel
reconstructed signals generated with the PD controllers. The torques generated with the PD controllers
and the torques computed from the model are presented in Figure 14.13a to Figure 14.13c. Apparently,
there is a close match between the experimental and the reconstructed signals in all three joints. This
implies a satisfactory estimation of the rigid-body dynamics. Moreover, since the model reconstructed the
control torques as the experiment was in progress, it follows that the dynamic model itself admits online
implementation. Sufficient quality in reconstructing the realistic dynamic behavior and the real-time
capability qualify the estimated model for model-based control purposes.
Copyright © 2005 by CRC Press LLC
14
-22 Robotics and Automation Handbook
−0.5036
0.6919
−0.1926
2.6462
0.1466
0.193
−2.5661
0.1875
−0.7763
1.3651
0.7217
2.8027
0 200 400 600 800 1000 1200 1400 1600 1800 2000
−0.0704
−0.0009
Number of samples
p
3
^
p
6
p
5
p
7
p
8
p
2
p
1
(a)
−0.0778
0.0473
−0.0183
0.0544
−0.5593
−0.2599
0.3397
0.4234
0.018
0.0459
0 200 400 600 800 1000 1200 1400 1600 1800 2000
1.5039
1.5679
Number of samples
p
11
p
10
p
13
p
9
p
12
p
14
(b)
FIGURE 14.12 Convergence of all BPS estimates.
14.6.6 Dynamics Not Covered with the Rigid-Body Dynamic Model
A motivation and procedures to identify and model dynamics not covered with a rigid-body dynamic
model are explained in Section 14.5. The frequency domain identification was applied on the RRR robot.
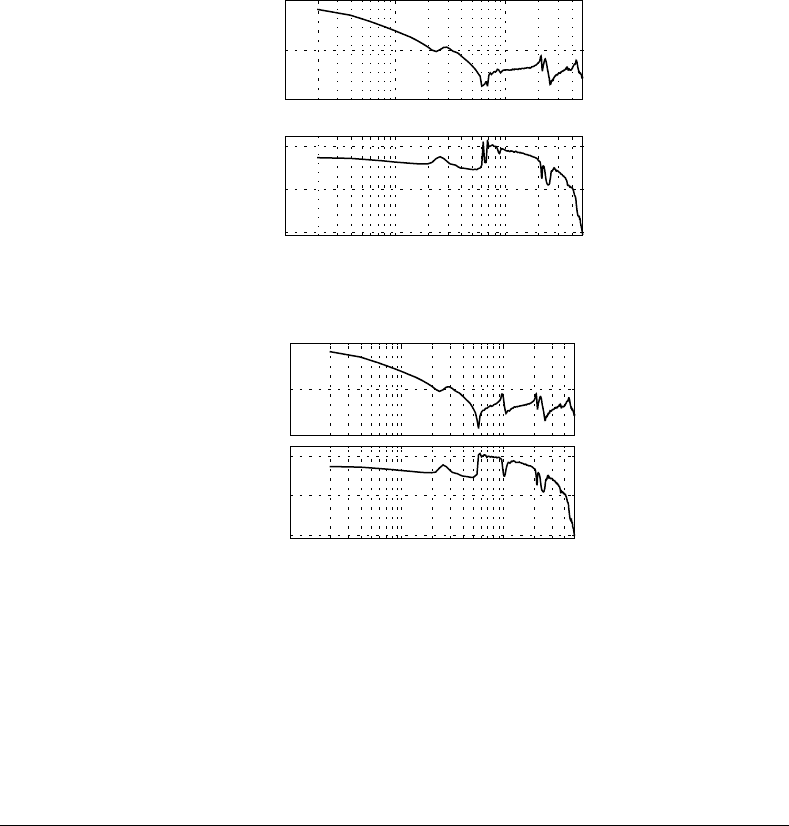
For illustration, Figure 14.14 presents frequency response functions (FRF) measured in the first joint, for
two different configurations in the remaining joints. The first FRF was obtained for the configuration
[q
2
, q
3
] = [0, π/2] [rad], which, according to the kinematic parameterisation shown in Figure 14.5,
corresponds to a horizontal orientation of the second link and vertical upwards position of the last link.
The second FRF corresponds to a fully horizontally stretched arm, i.e., [q
2
, q
3
] = [0, 0] [rad].
Both FRFs reveal rigid low frequency dynamics, i.e., the dynamics of a double integrator. Flexible effects
can be observed at higher frequencies. A modest resonance is apparent at 28 Hz, caused by insufficient
Copyright © 2005 by CRC Press LLC
Modeling and Identification for Robot Motion Control 14
-23
−15
20
0 10
−15
20
Time (s)
τ
1
(Nm)
|
PD feedback
Model
τ
1
(Nm)
(a)
−6
26
0
10
−6
26
Time (s)
τ
2
(Nm)
|
PD feedback
Model
τ
2
(Nm)
(b)
−2
5
τ
3
(Nm)
0
10
−2
5
Time (s)
PD feedback
Model
τ
3
(Nm)
|
(c)
FIGURE 14.13 Control torques produced with decentralized PD controllers and with the rigid-body dynamic model
in closed-form (measured in the experimental writing task).
stiffness in mounting the robot base to the floor. Being highly damped and with a temporary phase lead (see
the phase plots), it is not a problem for stability. However, it may cause vibrations of the robot mechanism
and consequently degrade the robot performance. At higher frequencies (above 80 Hz), more profound
resonances can be noticed. Their frequencies and damping factors depend on the robot posture. They can
contribute to amplification of vibrations and noise levels in the covered frequency ranges, which would
degrade the performance of motion control. If amplified too much by feedback, these resonances may even
destabilize the closed-loop system. To achieve motion control of high performance, the observed flexible
effects must be taken into account during the feedback control design.
Copyright © 2005 by CRC Press LLC
14
-24 Robotics and Automation Handbook
−150
−95
−40
Magnitude (dB)
110
100
−700
−400
−100
Frequency (Hz)
Phase (
o
)
(a)
−150
−95
−40
Magnitude (dB)
1 10 100
−700
−400
−100
Frequency (Hz)
Phase (
o
)
(b)
FIGURE 14.14 Flexible dynamics for first joint corresponding to two fixed configurations of the remaining joints:
(a) [q
2
, q
3
] = [0, π/2] and (b) [q
2
, q
3
] = [0, 0].
14.7 Conclusions
This chapter deals with the problems of robot modeling and identification for high-performance model-
based motion control. A derivation of robot kinematic and dynamic models was explained. Modeling of
friction effects was also discussed. Use of a writing task to establish correctness of the models was suggested.
Guidelines for design of an exciting identification trajectory were given. A Kalman filtering technique for
online reconstruction of joint motions, speeds, and accelerations was explained. A straightforward but
efficient estimation of parameters of the rigid-body dynamic model with friction effects was described.
The effectiveness of the procedure was experimentally demonstrated on a direct-drive robot with three
revolute joints. For this robot, models of kinematics and rigid-body dynamics were derived in closed-
form, and presented in full detail. The correctness of the models was established in simulation. Results
of experimental estimation of the dynamic model parameters were presented. The appropriateness of the
dynamic model for model-based control purposes was verified. However, it was also indicated that this
model is still not sufficient for a perfect match to the real robot dynamics, as these dynamics may contain
more effects than covered by the rigid-body model. A procedure to identify the dynamics not covered by
the rigid-body model was proposed. With these additional dynamics available, more advanced feedback
control designs become possible.
Copyright © 2005 by CRC Press LLC
Modeling and Identification for Robot Motion Control 14
-25
References
[1] Sciavicco, L. and Siciliano, B., Modeling and Control of Robot Manipulators, McGraw-Hill, London,
1996.
[2] Vukobratovi
´
c, M. and Potkonjak, V., Dynamics of Manipulation Robots: Theory and Application,
Springer-Verlag, Berlin, 1982.
[3] Fu,K.S., Gonzales, R.C., and Lee, C.S.G., Robotics: Control,Sensing, Vision, and Intelligence, McGraw-
Hill, London, 1987.
[4] Kozlowski, K., Modeling and Identification in Robotics, Springer-Verlag, London, 1998.
[5] Asada, H. and Youcef-Toumi, K., Direct-Drive Robots: Theory and Practice, MIT Press, London, 1987.
[6] Nethery, J. and Spong, M.W., Robotica: A Mathematica package for robot analysis, IEEE Rob. Autom.
Mag., 1, 13, 1994.
[7] Corke, P.I., A robotics toolbox for MATLAB, IEEE Rob. Autom. Mag., 3, 24, 1996.
[8] Bennnett, D.J. and Hollerbach, J.M., Autonomous calibration of single-loop closed kinematic chains
formed by manipulators with passive endpoint constraints, IEEE Trans. Rob. Autom., 7, 597, 1991.
[9] B
´
elanger, P.R., Estimation of angular velocity and acceleration from shaft encoder measurements,
in Proc. IEEE Int. Conf. Rob. Autom., Nice, France, 1992, 585.
[10] B
´
elanger, P.R., Dobrovolny, P., Helmy, A., and Zhang, X., Estimation of angular velocity and accel-
eration from shaft-encoder measurements, Int. J. Rob. Res., 17, 1225, 1998.
[11] Swevers, J., Ganseman, C., Tukel, D.B., de Schutter, J., and van Brussel, H., Optimal robot excitation
and identification, IEEE Trans. Rob. Autom., 13, 730, 1997.
[12] Calafiore, G., Indri, M., and Bona, B., Robot dynamic calibration: Optimal excitation trajectories
and experimental parameter estimation, J. Rob. Syst., 18, 55, 2001.
[13] Potkonjak, V., Tzafestas, S., Kostic, D., Djordjevic, G., and Rasic, M., Illustrating man-machine
motion analogy in robotics — the handwriting problem, IEEE Rob. Autom. Mag., 10, 35, 2003.
[14] Mayeda, H., Yoshida, K., and Osuka, K., Base parameters of manipulator dynamic models, IEEE
Trans. Rob. Autom., 6, 312, 1990.
[15] Armstrong-H
´
elouvry, B., Dupont, P., and Canudas de Wit, C., A survey of models, analysis tools
and compensation methods for the control of machines with friction, Automatica, 30, 1083,
1994.
[16] Olsson, H.,
◦◦
Astr
¨
om, K.J., Canudas de Wit, C., G
¨
afvert, M., and Lischinsky, P., Friction models and
friction compensation, Europ. J. Control, 4, 176, 1998.
[17] Swevers, J., Al-Bender, F., Ganseman, C.G., and Prajogo, T., An integrated friction model structure
with improved presliding behavior for accurate friction compensation, IEEE Trans. Autom. Control,
45, 675, 2000.
[18] Barabanov, N. and Ortega, R., Necessary and sufficient conditions for passivity of the LuGre friction
model, IEEE Trans. Aut. Control, 45, 830, 2000.
[19] Hensen, R.H.A., Angelis, G.Z., Van de Molengraft, M.J.G., De Jager, A.G., and Kok, J.J., Grey-box
modeling of friction: an experimental case study, Europ. J. Contr., 6, 258, 2000.
[20] Hensen, R.H.A., Van de Molengraft, M.J.G., and Steinbuch, M., Frequency domain identification
of dynamic friction model parameters, IEEE Trans. on Contr. Syst. Tech., 10, 191, 2001.
[21] Golub, G.H. and van Loan, C.F., Matrix computations, John Hopkins University Press, London,
1996.
[22] Slotine, J.J.E. and Li, W., Applied Nonlinear Control, Prentice Hall, Upper Saddle River, NJ, 1991.
[23] Nijmeijer, H. and Van der Schaft, A., Nonlinear Dynamical Control Systems, Springer-Verlag, Berlin,
1991.
[24] Pintelon, R. and Schoukens, J., System Identification: A Frequency Domain Approach, IEEE Press,
Piscataway, NJ, 2001.
[25] Sanathanan, C.K. and Koerner, J., Transfer function synthesis as a ratio of two complex polynomials,
IEEE Trans. Autom. Control, 8, 56, 1963.
Copyright © 2005 by CRC Press LLC
