Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.


8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.4. Влияние шероховатости стенки трубы на коэффициент сопротивления
Гидрогазодинамика. Учеб. пособие 191
Рис. 8.6
Здесь выполняется линейный закон сопротивления, выраженный ра-
венством (8.12
),
,64
Re
64
ср
dV
а сопротивление (перепад давления вдоль потока), определяемое фор-
мулой (8.11
),
2
2
ср
V
d
l
P
оказывается пропорциональным первой степени скорости, т. е.
.~
ср
VP
В пределах второй области
также не зависит от шероховатости, а за-
висимость этой величины от числа Re удовлетворяет формуле Блазиуса для
сопротивления гладких труб
25,0
Re
3164,0
,
благодаря чему она в логарифмических координатах изображается в
виде прямой. Протяженность этой области оказывается тем большей, чем
меньше относительная шероховатость
0
/ Rk
. Как видно из приведенных
формул, в этой области
75,1
~
V
P
.
В третьей области, относящейся к большим числам Рейнольдса, коэф-
фициент сопротивления перестает зависеть от числа Рейнольдса, а определя-
ется лишь значением относительной шероховатости. С ростом последней
увеличивается; при этом начало указанной области сдвигается в сторону
меньших значений числа Рейнольдса.
Поскольку в рассматриваемой области для каждого значения относи-
тельной шероховатости коэффициент сопротивления
представляет вели-
чину постоянную, то сопротивление трубы должно быть, в соответствии с
формулой (8.11
), пропорционально квадрату скорости:
2
ср
VP
. Поэтому
область, о которой здесь идет речь, часто называют областью квадратичного
сопротивления.
Между второй и третьей областью лежит промежуточная область, в ко-
торой
зависит как от относительной шероховатости, так и от числа Рей-
нольдса, а сопротивление трубы пропорционально скорости в степени m:
m
VP
ср
, где m лежит в пределах 1,75 < m < 2,0.
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.4. Влияние шероховатости стенки трубы на коэффициент сопротивления
Гидрогазодинамика. Учеб. пособие 192
Перечисленные особенности для зависимости
от числа Рейнольдса
при турбулентном режиме движения жидкости можно объяснить, сопостав-
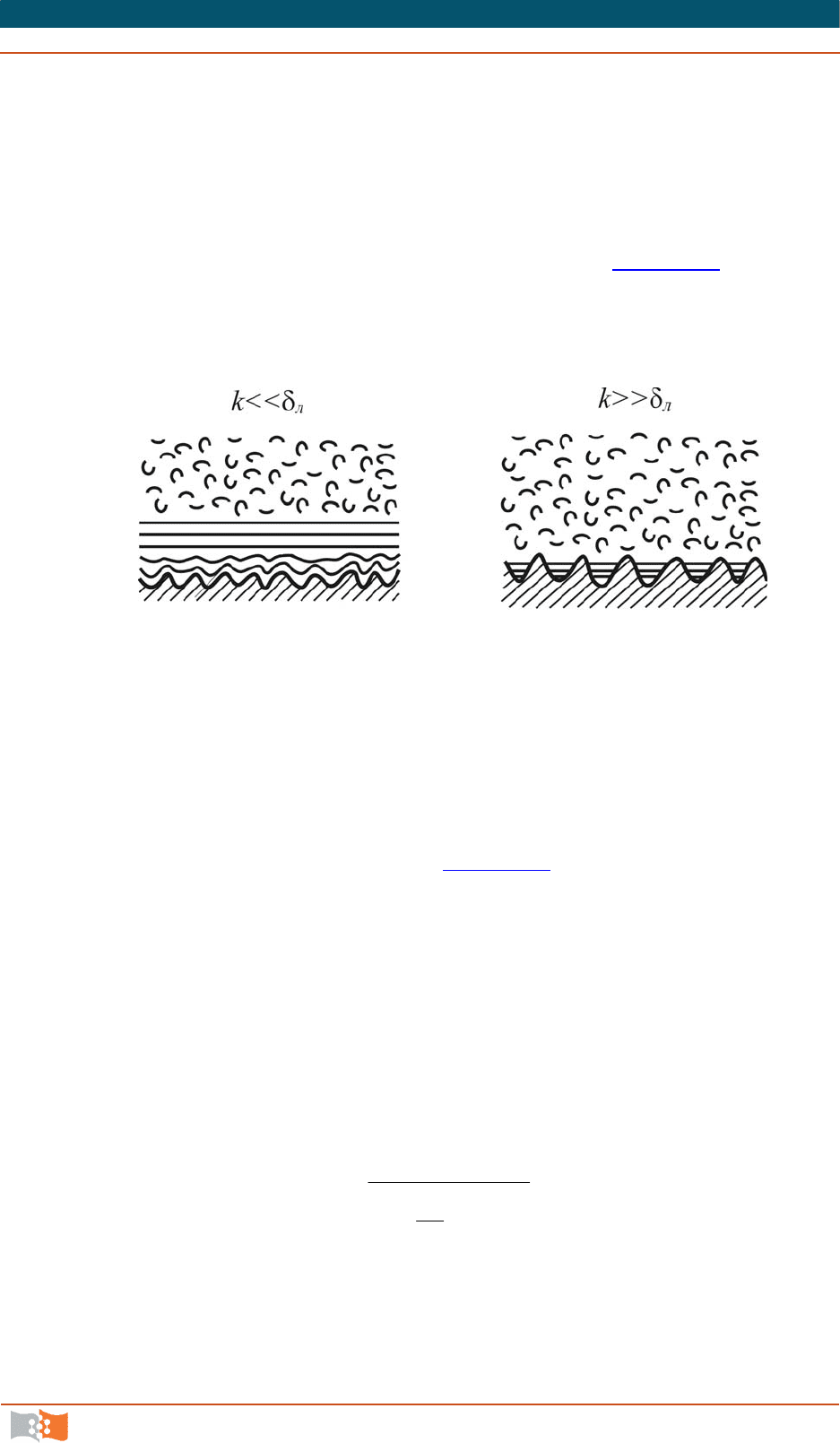
ляя среднюю высоту бугорков шероховатости k с толщиной ламинарного
подслоя
л
.
При k <<
л
, что имеет место при сравнительно малых числах Рей-
нольдса, бугорки шероховатости полностью покрыты ламинарным подслоем
и их обтекание не сопровождается вихреобразованием (рис. 8.7, а
). Следова-
тельно, в этом случае шероховатость не влияет на коэффициент сопротивле-
ния, и труба ведет себя в гидродинамическом отношении как гладкая, подчи-
няясь закону сопротивления Блазиуса (вторая область на графике Никурадзе).
а б
Рис. 8.7
Толщина ламинарного подслоя уменьшается с увеличением числа Рей-
нольдса, и при достаточно больших значениях последнего оказывается, что
л
k
. В этом случае бугорки шероховатости практически целиком выходят
в турбулентное ядро потока и их обтекание, как тел плохо обтекаемой фор-
мы, происходит с образованием вихрей (рис. 8.7, б
). При таком характере об-
текания вязкие силы мало существенны по сравнению с силами инерцион-
ными и коэффициент сопротивления перестает зависеть от числа Рейнольдса,
что и объясняет наличие третьей области на графике Никурадзе.
Как указывалось, в этой области
зависит только от относительной шеро-
ховатости. Чтобы подчеркнуть это, режим обтекания шероховатости, отвечаю-
щий этой области, ранее названной областью квадратичного сопротивления,
именуют режимом развитой шероховатости.
Закон сопротивления для указанного режима выражается следующей
формулой:
.
74,1lg2
1
2
0
k
R
(8.51)
Область, занимающая на графике Никурадзе промежуточное положе-
ние между второй и третьей областью, отвечает случаю, когда
k
и
л
оказы-
ваются величинами одного и того же порядка.

Гидрогазодинамика. Учеб. пособие 193
9
9
.
.
П
П
О
О
Г
Г
Р
Р
А
А
Н
Н
И
И
Ч
Ч
Н
Н
Ы
Ы
Й
Й
С
С
Л
Л
О
О
Й
Й
И
И
П
П
Р
Р
О
О
Ц
Ц
Е
Е
С
С
С
С
Ы
Ы
Т
Т
Е
Е
П
П
Л
Л
О
О
-
-
И
И
М
М
А
А
С
С
С
С
О
О
О
О
Б
Б
М
М
Е
Е
Н
Н
А
А
9
9
.
.
1
1
.
.
П
П
о
о
н
н
я
я
т
т
и
и
е
е
о
о
п
п
о
о
г
г
р
р
а
а
н
н
и
и
ч
ч
н
н
о
о
м
м
с
с
л
л
о
о
е
е
Ранее отмечалось, что при очень больших значениях числа Рейнольдса,
свидетельствующих о большом преобладании инерционных сил над силами
вязкости, можно последними пренебречь и рассматривать движущуюся жид-
кость при таких Re как идеальную. Однако такое приближение не может
быть распространено на ту область течения жидкости, которая непосредст-
венно примыкает к поверхности твердого тела и на которой сказыв
ает
ся тор-
мозящее влияние поверхности. В этой, вообще говоря, узкой области имеет
место резкое изменение скорости по нормали к поверхности от нулевого зна-
чения, которое она имеет на самой поверхности, до значения, сравнимого с
тем, которое устанавливается вдали от поверхности. Этот тонкий слой жид-
кости получил название пограничного слоя. В этом слое п
р
енебрегать силами
вязкости нельзя. Наоборот, благодаря большим градиентам скорости они
приобретают здесь решающее значение. Но сведение сферы влияния этих сил
к узкой области пограничного слоя позволяет внести значительные упроще-
ния в уравнения движения вязкой жидкости и делает возможным их интегри-
рование.
Явления, происходящие в пограничном слое, играют существ
енную
роль как в
определении величины гидродинамического сопротивления, так и
в определении интенсивности процессов тепло- и массообмена между твер-
дым телом и обтекающей его жидкостью
.
Движение жидкости в пограничном слое может быть как ламинарным,
так и турбулентным.
Более строго интенсивность этих двух процессов следует поставить в связь с существо-
ванием теплового и диффузионного пограничного слоя.
9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
Гидрогазодинамика. Учеб. пособие 194
9
9
.
.
2
2
.
.
У
У
р
р
а
а
в
в
н
н
е
е
н
н
и
и
я
я
л
л
а
а
м
м
и
и
н
н
а
а
р
р
н
н
о
о
г
г
о
о
п
п
о
о
г
г
р
р
а
а
н
н
и
и
ч
ч
н
н
о
о
г
г
о
о
с
с
л
л
о
о
я
я
Для более легкого восприятия рассмотрим двухмерное обтекание пло-
ской поверхности тела несжимаемой жидкостью. Направим ось
1
x
вдоль по-
верхности по направлению потока, а ось
2
x
– перпендикулярно к поверхно-
сти (рис. 9.1
). Будем полагать поток стационарным и массовые силы отсутст-
вующими. Тогда уравнения Навье Стокса и уравнение неразрывности при-
нимают вид
.0
;
1
;
1
2
2
1
1
2
2
2
2
2
1
2
2
22
2
2
1
2
1
2
2
1
2
2
1
1
2
12
1
2
1
1
1
x
V
x
V
x
V
x
V
x
P
x
V
V
x
V
V
x
V
x
V
x
P
x
V
V
x
V
V
(9.1)
Обозначим скорость за пределами пограничного слоя (иными словами,
скорость набегающего потока) через U. Поскольку вне пограничного слоя
жидкость рассматривается как идеальная, движение частиц которой проис-
ходит без деформации и, следовательно, не сопровождается вращением, то в
указанной области поток можно считать потенциальным.
Рис. 9.1
Преобразуем систему уравнений (9.1
) к безразмерному виду, восполь-
зовавшись для этой цели в качестве характерных величин протяженностью
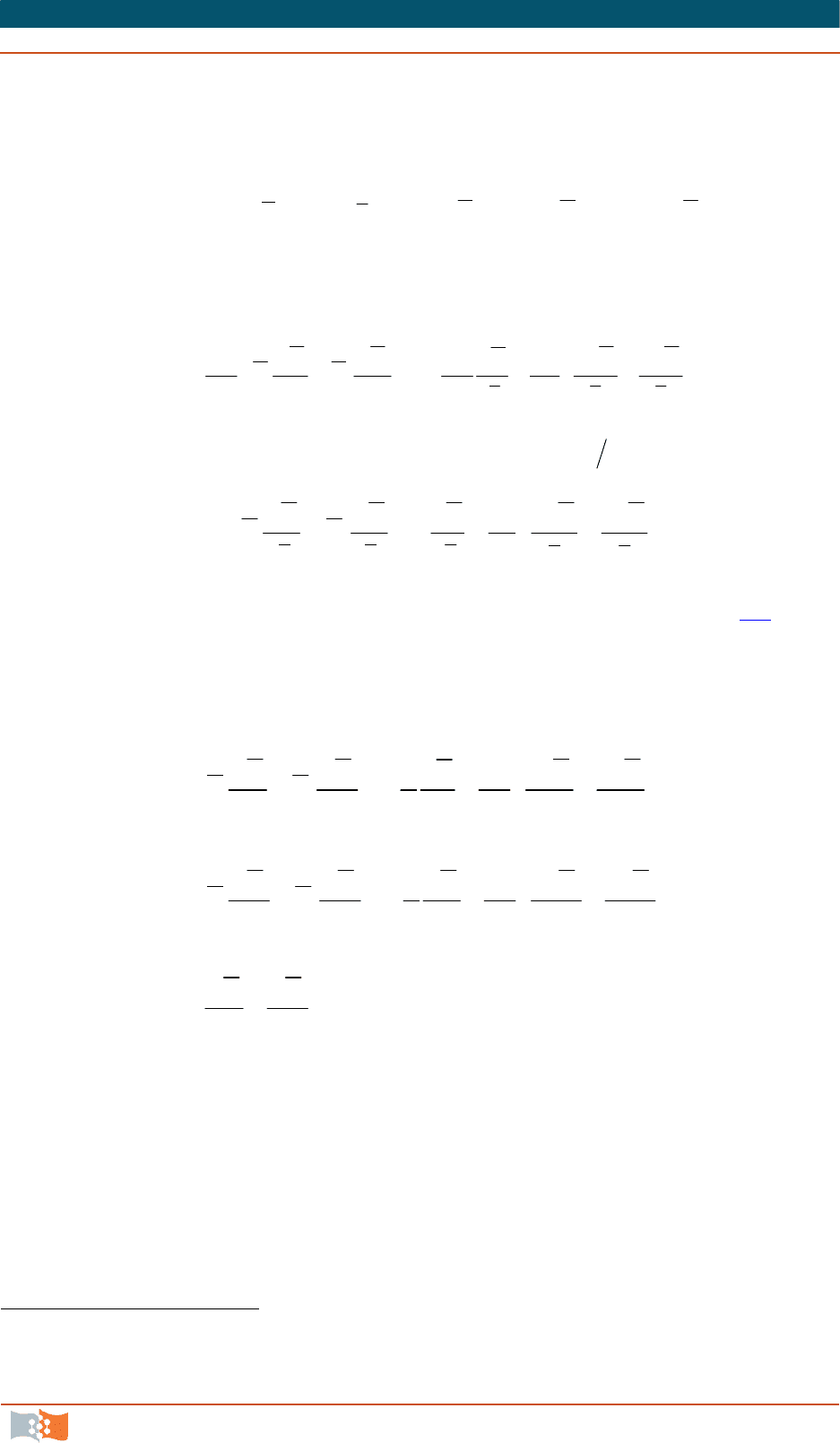
9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 195
поверхности тела в направлении обтекания
l
и скоростью набегающего по-
тенциального потока
U ; в качестве масштаба преобразования давления вы-
берем удвоенный динамический напор потока
2
U
. Тогда будем иметь
;
11
xlx
;
22
xlx
;
11
VUV
;
22
VUV
.
2
PUP
Подставив соответствующие величины в первое из уравнений системы
(9.1), получим
,
2
2
1
2
2
1
1
2
2
1
2
2
2
2
1
1
1
2
x
V
x
V
l
U
x
P
l
U
x
V
V
x
V
V
l
U
или после деления обеих частей уравнения на
lU
2
2
2
1
2
2
1
1
2
12
1
2
1
1
1
x
V
x
V
Ulx
P
x
V
V
x
V
V
.
Если придать аналогичный вид второй компоненте системы (9.1), пре-
образовать к безразмерной форме уравнение неразрывности и при этом
учесть, что
Re
/
U
l
– число Рейнольдса, определенное по скорости набе-
гающего потока, получим
.0
;
Re
11
;
Re
11
2
2
1
1
2
2
2
2
2
1
2
2
22
2
2
1
2
1
2
2
1
2
2
1
1
2
12
2
2
1
1
1
x
V
x
V
x
V
x
V
x
P
x
V
V
x
V
V
x
V
x
V
x
P
x
V
V
x
V
V
(9.2)
Такая форма записи уравнений движения удобна для анализа порядка
величины отдельных членов, входящих в эти уравнения, и для выявления тех
упрощений, которые могут быть сделаны при применении этих уравнений к
пограничному слою.
Обозначим толщину пограничного слоя через δ и будем понимать под
этой величиной то расстояние от поверхности, на котором скорость стано-
вится близка к скорости основного (набегающего) потока
.
Вообще говоря, толщина пограничного слоя является величиной условной, по-
скольку скорость
V
1
по мере удаления от поверхности приближается к значению U асим-
9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 196
Прежде чем приступить к анализу уравнений (9.2), отметим, что без-
размерная координата
1
x
изменяется в пределах от нуля до единицы (при
lx
1
). Безразмерной координатой
2
x
приходится в данной задаче опериро-
вать только в пределах пограничного слоя, где ее значение изменяется в ин-
тервале от нуля до
, здесь
l
безразмерная толщина пограничного слоя.
Безразмерная компонента скорости
1
V
изменяется в пределах от нуля
до единицы (при
1
VU
, т. е. на внешней границе пограничного слоя).
Обратимся теперь к уравнению неразрывности
.0
2
2
1
1
x
V
x
V
Определяя порядок производной
11
/ xV
как отношение предельных
изменений величин
1
V
и
1
x
, находим, что он равен единице. Из рассматри-
ваемого уравнения следует, что производная
22
/ xV
также имеет порядок,
равный единице, а т. к. предельное значение безразмерной координаты
2
x
равно
, то и предельный порядок величины
2
V
будет таким же.
Запишем теперь под членами первых двух уравнений системы (9.2
) их
порядки и при сопоставлении отдельных членов этих уравнений друг с дру-
гом будем считать
1
. Производную
1
/ xP
, поскольку она не связана с
, следует рассматривать как величину конечную, и ее порядок можно по-
ложить равным единице. Относительно порядка производной
2
/ xP
нельзя
сделать никаких предварительных предположений. Таким образом, можем
записать
;
Re
1
2
2
1
2
2
1
1
2
12
1
2
1
1
1
x
V
x
V
x
P
x
V
V
x
V
V
2
2
2
2
2
2
1
2
2
22
2
2
1
2
1
1
.
Re
1
x
V
x
V
x
P
x
V
V
x
V
V
Очевидно, что в правой части первого уравнения можно пренебречь
величиной
2
11
2
/ xV
по сравнению с
2
21
2
/ xV
величиной, порядок которой
много больше единицы. Из этого уравнения следует, что величина
2
2
1
2
Re
1
x
V
должна иметь порядок, равный единице, т. е. такой же, как и все остальные
члены этого уравнения:
птотически. Обычно принято определять как расстояние от поверхности, на котором
V
1
= (0,980,99)U.

9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 197
1~
Re
1
2
2
2
x
V
x
.
Отсюда вытекает, что порядок величины
Re
/
1 равен
2
, а
Re
1
~
или,
учитывая, что
l/
,
.
Re
~
l
(9.3)
Поскольку в основе теории пограничного слоя лежит предположение о
том, что число Рейнольдса, характеризующее поток, велико, то из соотноше-
ния (9.3
) становится очевидным, что толщина пограничного слоя
пред-
ставляет ничтожно малую величину по сравнению с размерами обтекаемого
тела. Как будет видно из дальнейшего, порядок зависимости
от числа Re,
выраженный соотношением (9.3
), подтверждается точным расчетом.
Обратимся теперь ко второму уравнению. Порядок членов, содержа-
щихся в левой части этого уравнения, равен
, слагаемые, стоящие в скоб-
ках, после умножения на
Re
1
приобретают соответственно порядки
3
и
,
поэтому производная
2
/ xdPd
также должна иметь порядок
. Следователь-
но, рассматриваемое уравнение можно полностью отбросить и, в частности,
пренебречь изменением давления в пограничном слое в направлении, нор-
мальном к поверхности, считая, что
2
/ xdPd
.
Это означает, что в принятом приближении давление в пограничном
слое остается таким же, как вне пограничного слоя, и является функцией
только координаты х. Поэтому в первом уравнении системы (9.2
) можно вме-
сто частной производной
1
/ xdPd
записать полную производную
1
/ xdPd
.
Таким образом, из системы уравнений (9.2
) второе уравнение можно
целиком исключить, а в первом сделать указанные упрощения. Возвращая
оставшимся уравнениям размерную форму, получим
.0
;
1
2
2
1
1
2
2
1
2
11
1
2
1
1
1
x
V
x
V
x
V
x
P
x
V
V
x
V
V
(9.4)
Уравнения (9.4
) называются уравнениями Прандтля для пограничного
слоя. Будучи получены из уравнения Навье Стокса, в котором пульсацион-

9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 198
ные скорости в явной форме не представлены, они пригодны лишь для опи-
сания движения в ламинарном пограничном слое.
Применим к внешней границе пограничного слоя уравнение Бернулли
Эйлера для потенциального потока (5.63
), в котором для данного случая гео-
метрический напор
z
рассматривается как величина постоянная:
const
2
2
P
U
.
Дифференцируя это уравнение по
1
x
, находим, что
11
1
dx
dU
U
dx
dP
.
Подставляя это выражение в уравнение Прандтля, получим систему
уравнений ламинарного пограничного слоя в более удобной форме:
.
0
;
2
2
1
1
2
2
1
2
12
1
2
1
1
1
x
V
x
V
x
V
dx
dU
U
x
V
V
x
V
V
(9.5)
Эти уравнения, полученные для случая обтекания плоской поверхно-
сти, пригодны и для искривленных поверхностей, если радиус кривизны на-
много превосходит толщину пограничного слоя
.
Граничные условия для этих уравнений имеют вид
. при
; 0 при
0
21
221
xUV
xVV
(9.6)
Наиболее простой, но приближенный метод решения системы уравне-
ний (9.5
) основан на сведении этой системы к т. н. уравнению импульсов
Кармана. Преобразуем инерционные члены, входящие в первое уравнение
системы (9.6
), следующим образом:
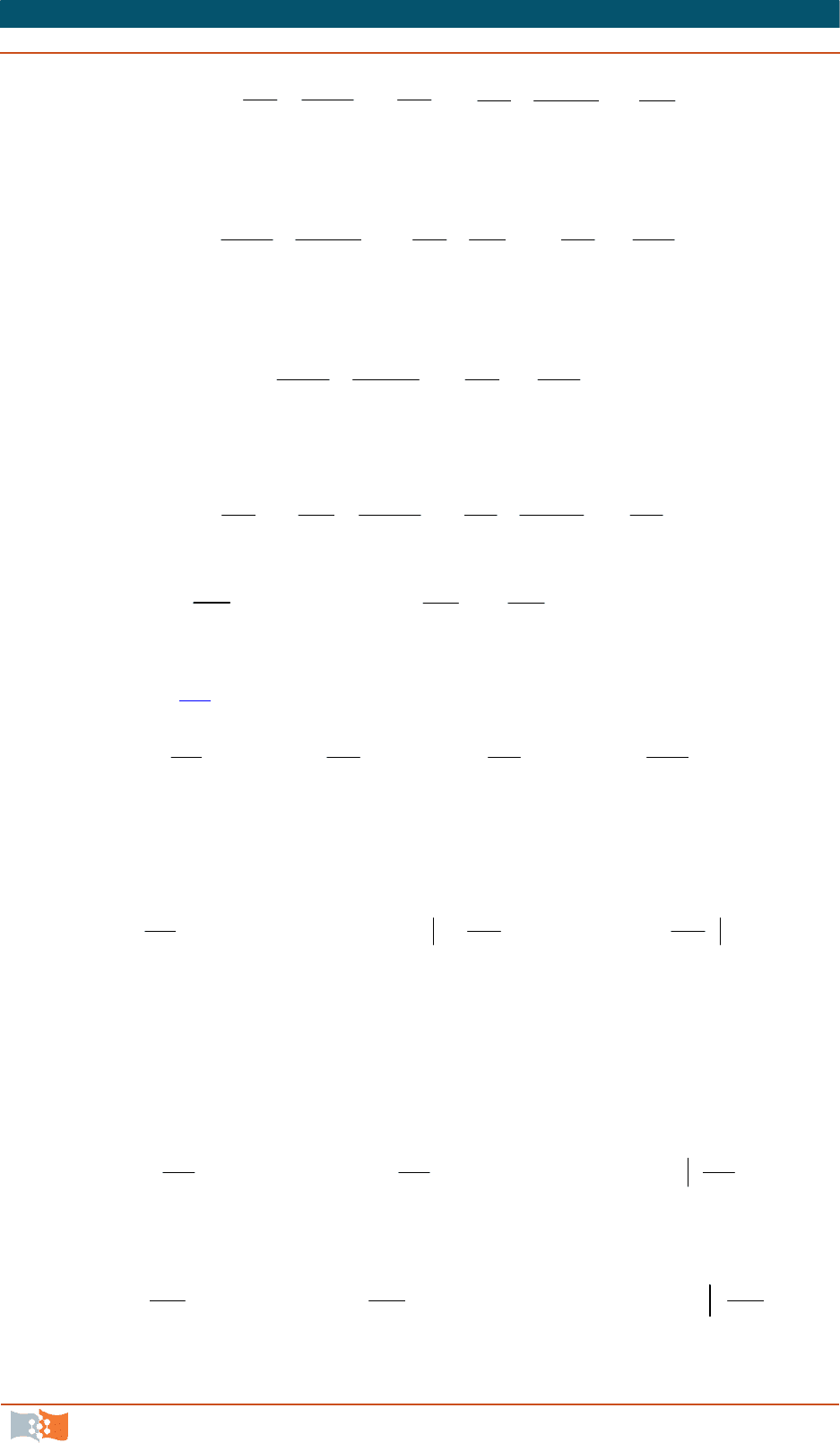
9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 199
;
1
1
1
1
2
1
1
1
1
x
V
V
x
V
x
V
V
;
2
2
1
2
21
1
1
2
x
V
V
x
VV
x
V
V
Тогда можем записать
,
2
2
1
2
12
2
1
1
1
2
21
1
2
1
x
V
dx
dU
U
x
V
x
V
V
x
VV
x
V
или, используя уравнение неразрывности,
,
2
2
1
2
12
21
1
2
1
x
V
dx
dU
U
x
VV
x
V
(9.7)
Далее запишем уравнение неразрывности в форме
,0
2
2
2
2
1
1
1
1
2
2
1
1
x
U
V
x
UV
x
U
V
x
UV
x
V
U
x
V
U
где член
2
2
x
U
V
равен нулю, a
,
1
1
1
1
x
dU
V
x
U
V
поскольку скорость набе-
гающего потока
U от координаты
2
x
не зависит, и вычтем из этого уравне-
ния выражение (9.7
). Тогда будем иметь
.
2
2
1
2
1
1
12
2
11
1
x
V
VU
x
U
VUV
x
VUV
x
(9.8)
Проинтегрировав это уравнение по
2
x
в пределах от нуля до толщины
пограничного слоя
, получим
.
0
2
1
2
0
1
1
0
12211
0
1
x
V
dxVU
dx
dU
VUVdxVUV
x
(9.9)
При интегрировании следует учесть, что
является величиной пере-
менной, зависящей от координаты
1
x
.
Первый интеграл представляет одно из слагаемых производной, взятой
по координате
1
x
от интеграла с переменным верхним пределом:
.
1
0
11211
0
1
21
0
1
1
11
dx
d
VUVdxVUV
x
dxVUV
dx
d
xx
Следовательно,
.
1
0
112
0
11
1
0
211
1
dx
d
VUVdxVUV
dx
d
dxVUV
x

9. ПОГРАНИЧНЫЙ СЛОЙ И ПРОЦЕССЫ ТЕПЛО- И МАССООБМЕНА
9.2. Уравнения ламинарного пограничного слоя
Гидрогазодинамика. Учеб. пособие 200
При интегрировании уравнения (9.9) используем граничные условия
(9.6
), присоединив к ним некоторые дополнительные условия:
.0 , ïðè
, , 0 ïðè
2
1
12
2
1
2
1
212
x
V
UVx
x
V
x
V
VVx
w
(9.10)
Находим значения отдельных составляющих уравнения (9.9
):
;0
0
11
VUV
;0
0
12
VUV
.
0
2
1
0
2
1
2
w
x
x
V
x
V
После подстановки всех последних равенств уравнение приобретет вид
,
2
0
1
1
21
0
1
1
w
dxVU
dx
dU
dxVUV
dx
d
или
.11
2
0
1
1
2
1
0
1
2
1
w
dx
U
V
dx
dU
Udx
U
V
U
V
U
dx
d
(9.11)
Введем следующие обозначения:
;1
0
2
1
dx
U
V
(9.12)
.1
0
2
11
dx
U
V
U
V
(9.13)
Первый из этих интегралов получил название толщины вытеснения, а
второй – толщины потери импульса. Подставив эти величины в уравнение
(9.11), придадим ему вид
,
1
**2
1
w
dx
dU
UU
dx
d
или после дифференцирования первого слагаемого
