Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

Подождите немного. Документ загружается.

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.2. Основные элементы теории турбулентного движения



Гидрогазодинамика. Учеб. пособие 181

массами жидкости, переходящими из одного слоя в другой под влиянием

пульсации скорости.

Полное касательное напряжение трения можно представить как сумму

молекулярного и турбулентного напряжения:



1212

AP 

(8.23)

В отдалении от обтекаемой твердой поверхности (стенки), где пульса-

ции скорости велики, величина

в уравнении (8.23) во много раз превосхо-

дит величину



, так что последней можно для этой области потока пренеб-

речь. По мере приближения к стенке пульсации скорости быстро уменьша-

ются. Уменьшается и величина

, становясь в самой непосредственной бли-

зости к стенке ничтожно малой по сравнению с



. На самой стенке

= 0 и

касательное напряжение определяется только молекулярной вязкостью и

градиентом скорости



















(8.24)

Наиболее простую физическую модель турбулентного потока, позво-

ляющую установить некоторые общие закономерности, дает гипотеза Пран-

дтля. Согласно этой гипотезе принимается, что в среднем абсолютные значе-

ния пульсационных скоростей одинаковы во всех направлениях (т. е. турбу-

лентность рассматривается как изотропная) и что эти величины пропорцио-

нальны градиенту скорости по нормали к направлению потока:

lVV 







(8.25)

Коэффициент пропорциональности

, имеющий размерность длины,

получил название длины пути перемешивания. Эта величина представляет

собой расстояние, которое успевает пройти некоторый малый объем жидко-

сти, вышедший из данного слоя, до того, как, смешавшись с окружающим

его потоком, он теряет свою индивидуальность, и может рассматриваться как

турбулентный аналог длины свободного пробега молекул в кинетической

теории газов.

Далее Прандтль принимает, что путь перемешивания пропорционален

расстояни

ю рассматриваемой точки потока от ст

енки, т. е.





, (8.26)

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.2. Основные элементы теории турбулентного движения



Гидрогазодинамика. Учеб. пособие 182

где   некоторая постоянная величина.

Из равенств (8.22

) и (8.25) вытекает следующее выражение для абсо-

лютной величины касательного турбулентного напряжения:

2112





















lVVP

(8.27)

Сравнивая правые части выражений (8.22

) и (8.27), находим

lA 

(8.28)

Как и в случае ламинарного потока, изучение турбулентного потока

жидкости в трубе сводится к выяснению характера распределения скорости

по сечению трубы и к установлению закона сопротивления движению. Вос-

пользуемся уравнением (8.23

), приняв в нем приближенно полное напряже-

ние трения величиной постоянной и равной напряжению трения на стенке

трубы, т. е.







const

Тогда уравнение (8.23

) перепишется в виде



(8.29)

Как уже отмечалось, вблизи стенки величина

ничтожно мала по

сравнению с



. Поэтому для пристеночной области потока, часто именуемой

ламинарным подслоем, можно в правой части уравнения (8.29

) пренебречь

вторым членом и написать (подстрочный индекс при скорости в дальнейшем

опускаем; для ламинарного подслоя можно также опустить черточку, озна-

чающую осреднение скорости)



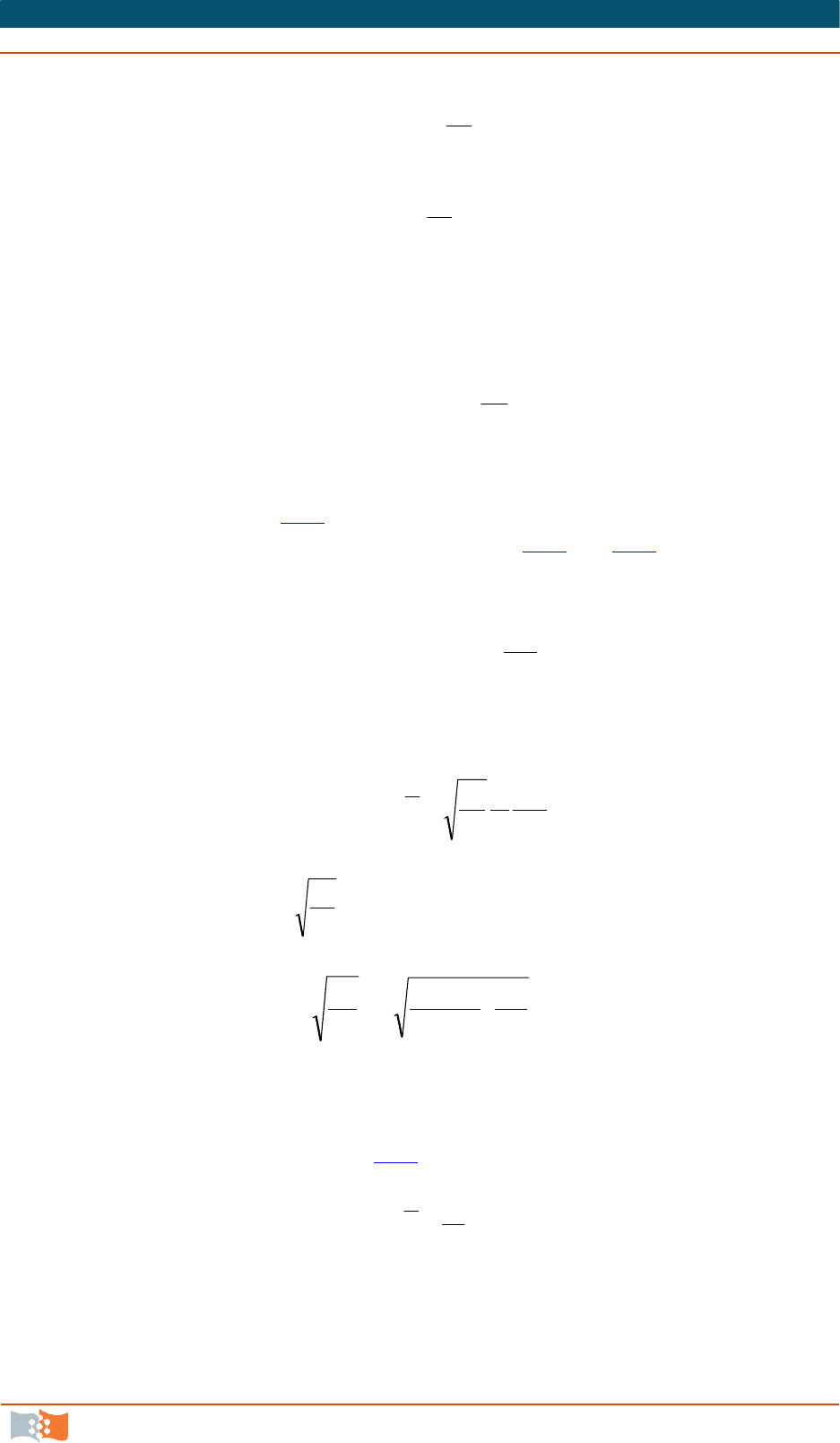
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 183

Отсюда

dxdV







Интегрируя, получаем

CxV









При

x

= 0, следовательно, постоянная интегрирования С = 0. Та-

ким образом, находим, что в ламинарном подслое распределение скорости

носит линейный характер:







. (8.30)

Обратимся теперь к турбулентному ядру потока. Для этой области по-

тока можно в уравнении (8.29

) пренебречь напряжением, обусловленным мо-

лекулярной вязкостью, и, используя равенства (8.28

) и (8.26), переписать его

в виде

















(8.31)

или после разделения переменных







(8.32)

Введем обозначение









Эта величина, имеющая размерность

,/:

322

см

кг

мс

мкг























получила название динамической скорости.

Интегрирование уравнения (8.32

) дает

.ln

V 







(8.33)

Для определения произвольной постоянной С следует в данном случае

привлечь пространственное условие, относящееся к границе раздела между

турбулентным ядром потока и ламинарным подслоем:

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 184











л2

(8.34)

Здесь



 толщина ламинарного подслоя;

 скорость на границе ла-

минарного подслоя.

В свою очередь, для определения



воспользуемся методом анализа

размерностей. Предположим, что толщина ламинарного подслоя зависит

только от вязкости и плотности жидкости и от напряжения трения на стенке

и что она может быть выражена в виде одночленной степенной функции от

этих величин



cba

 ,

где   некоторая безразмерная постоянная.

Формула размерности, эквивалентная этой зависимости, будет иметь

вид



cba







































Здесь через L, М и Т обозначены соответственно единицы длины, мас-

сы и времени.

Приравнивая показатели степени при одинаковых единицах в левой и

правой части формулы размерности, получим систему уравнений:

для L

cba





31 ;

для М

cba





;

для Т

ca 20





Решение этой системы дает



;

b

c

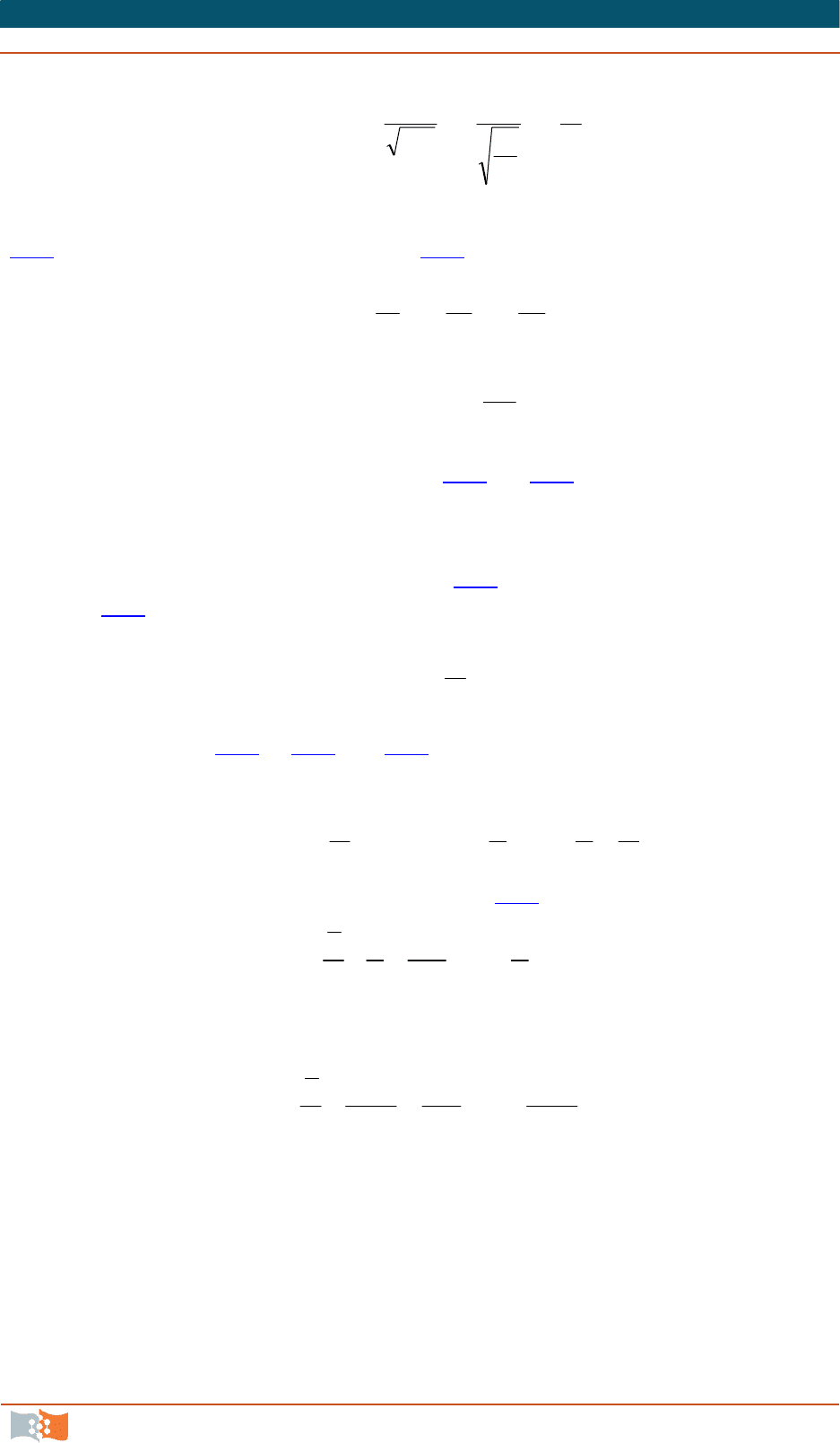
Таким образом, искомая зависимость принимает вид







8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 185

или























(8.35)

Толщину ламинарного подслоя можно также определить из уравнения

(8.30

) при пространственном условии (8.34); имеем

лл

V 



















Отсюда







(8.36)

Сравнивая правые части равенств (8.35) и (8.36), получим







(8.37)

Возвратимся теперь к уравнению (8.33). Используя пространственное

условие (8.34

), можем записать его для границы ламинарного подслоя в виде

.ln C

лл









(8.38)

Из равенств (8.35), (8.37) и (8.38) определяем произвольную постоян-

ную С:

.ln











































лл

Подставив это выражение в уравнение (8.33

), получим

,ln

























или, переходя от натуральных логарифмов к десятичным,

.lg

303,2

























(8.39)

Числовые значения постоянных



и α были определены Никурадзе на

основе тщательных измерений распределения скоростей в круглой трубе,

проведенных в широком диапазоне чисел Рейнольдса (от 4·103 до 3,24·106);

оказалось:

.5,11 , 4,0 

Величины



и α, как не зависящие от числа Рейнольдса, получили на-

звание универсальных постоянных турбулентного движения. Подставив

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 186

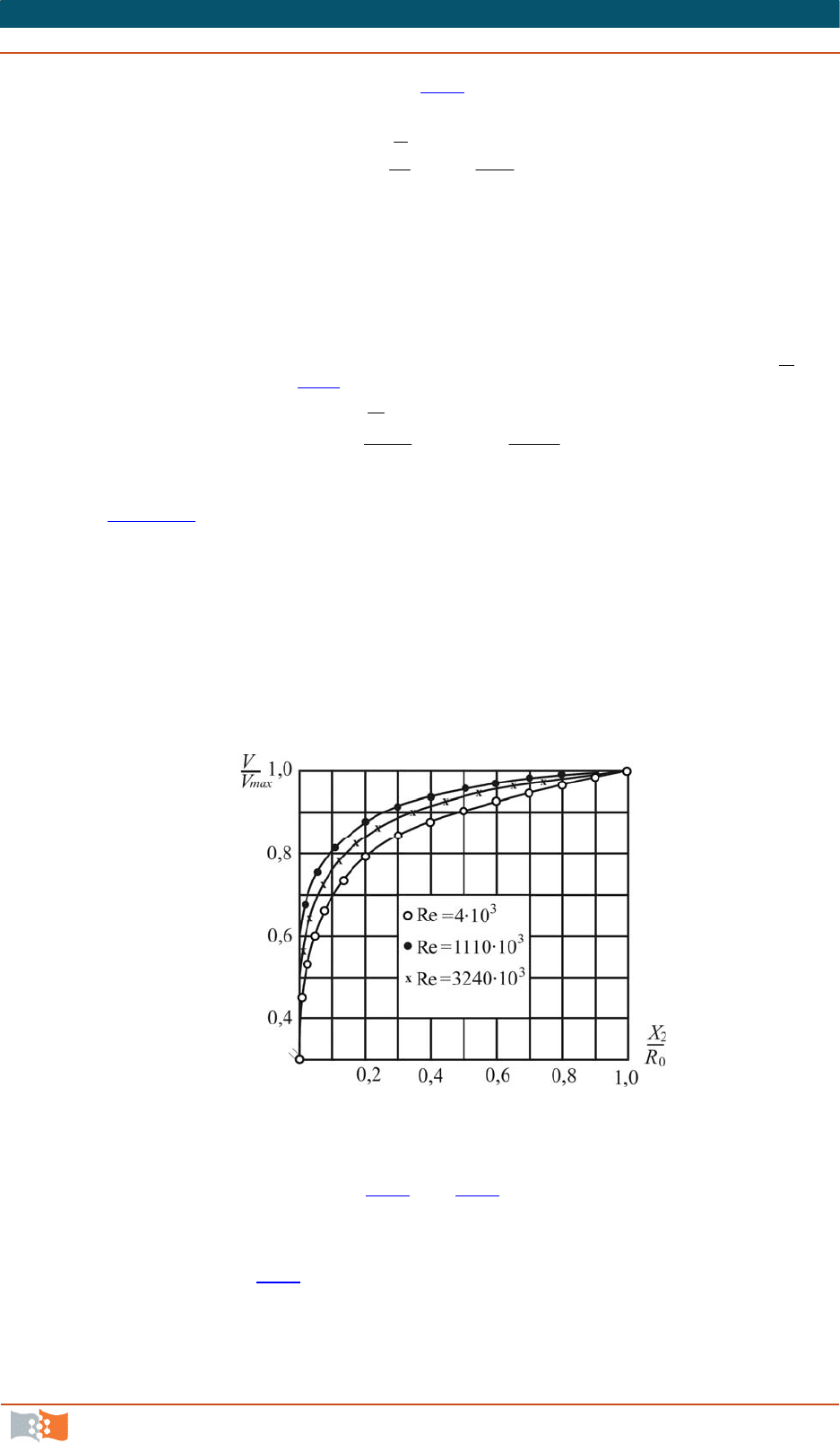
значения этих величин в выражение (8.39), получим окончательное уравне-

ние для распределения скоростей в турбулентном ядре потока:

.5,5lg75,5







(8.40)

Это уравнение выражает т. н. универсальный логарифмический закон

распределения скоростей. Теорию турбулентного движения, на которой ос-

новано полученное уравнение, следует рассматривать как полуэмпириче-

скую, поскольку для определения постоянных



и α приходится прибегать к

помощи эксперимента.

Полагая в уравнении (8.40

)



, найдем скорость на оси трубы (

max

5,5lg75,5

0max







. (8.41)

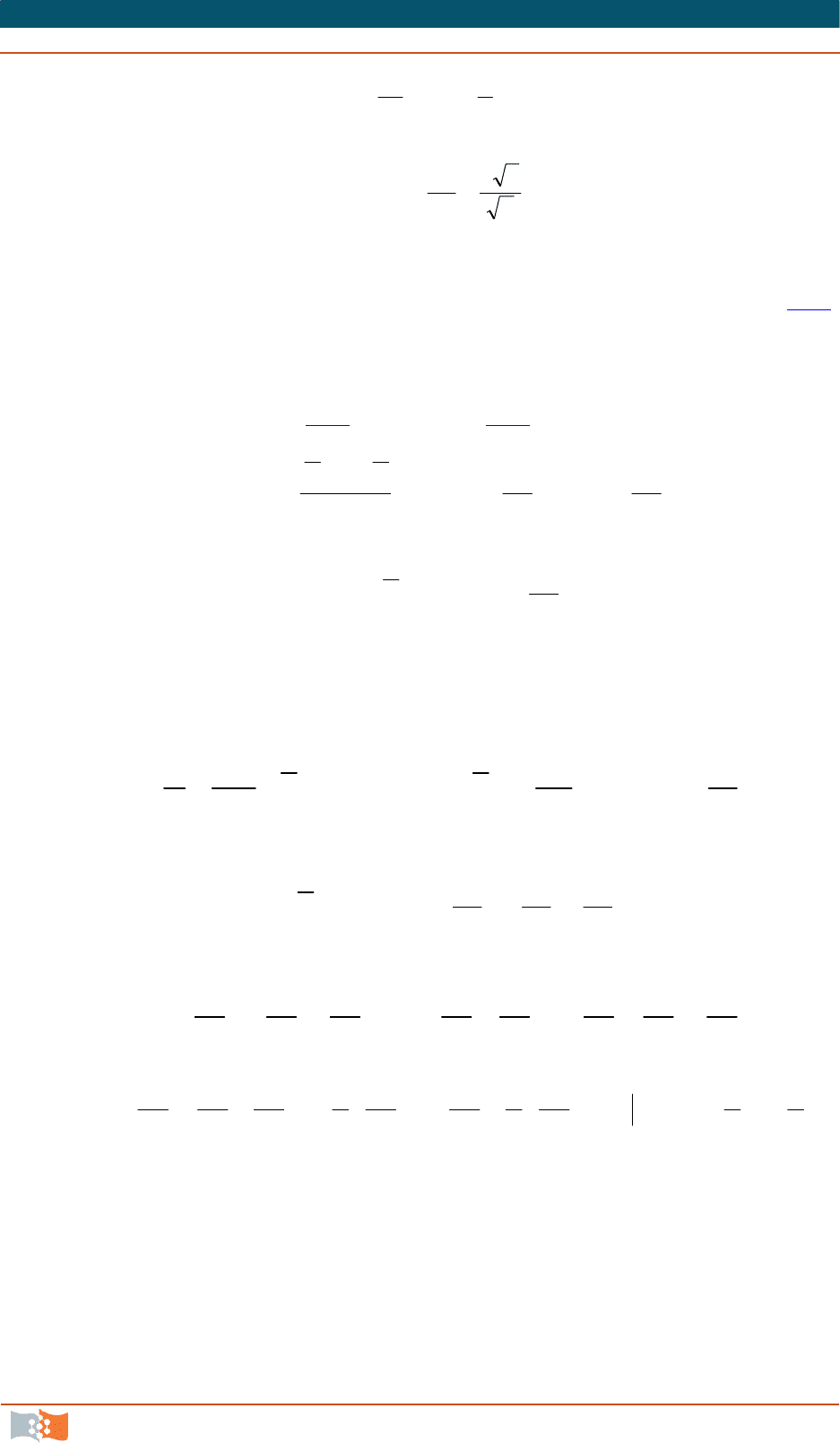
На рис. 8.5 представлены некоторые из экспериментальных кривых

распределения скоростей по сечению круглой трубы, полученных Никурадзе.

Более высоким значениям числа Рейнольдса отвечает более равномерное

распределение скорости, или, как говорят, более заполненный профиль ско-

ростей. По этой причине с увеличением числа Рейнольдса уменьшается от-

ношение максимальной скорости к средней скорости, определяемой по рас-

ходу. Это отношение изменяется от 1,3 при Re = 5000 до 1,15 при Re

= 3·106,

тогда как при

ламинарном движении в круглой трубе оно равно 2.

Рис. 8.5

Использование уравнений (8.40

) и (8.41) требует знания динамической

скорости V

. Определение этой величины связано с задачей об определении

коэффициента сопротивления трубы при турбулентном движении.

Из соотношения (8.14

) следует, что

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 187

ср











Отсюда

ср







(8.42)

Среднюю скорость по сечению можно рассматривать как величину из-

вестную, задаваемую по расходу. Две другие величины в соотношении (8.42

)

являются неизвестными, и для их определения необходимо еще одно уравне-

ние. В качестве такового может служить уравнение связи между величинами

max

, V

ср

Вычтем из равенства (8.41

) равенство (8.40), тогда получим

.ln5,2lg75,5

max







(8.43)

Отсюда

.ln5,2

max

VVV





Воспользуемся этим выражением для определения средней скорости по

сечению (метод расчета остается таким же, как для случая ламинарного дви-

жения):

 

.ln15

max

max2

ñð







































VdxxRV

Находим интеграл:

lnlnln1







































































































































Следовательно,

,75,3

maxср 





VVV

или

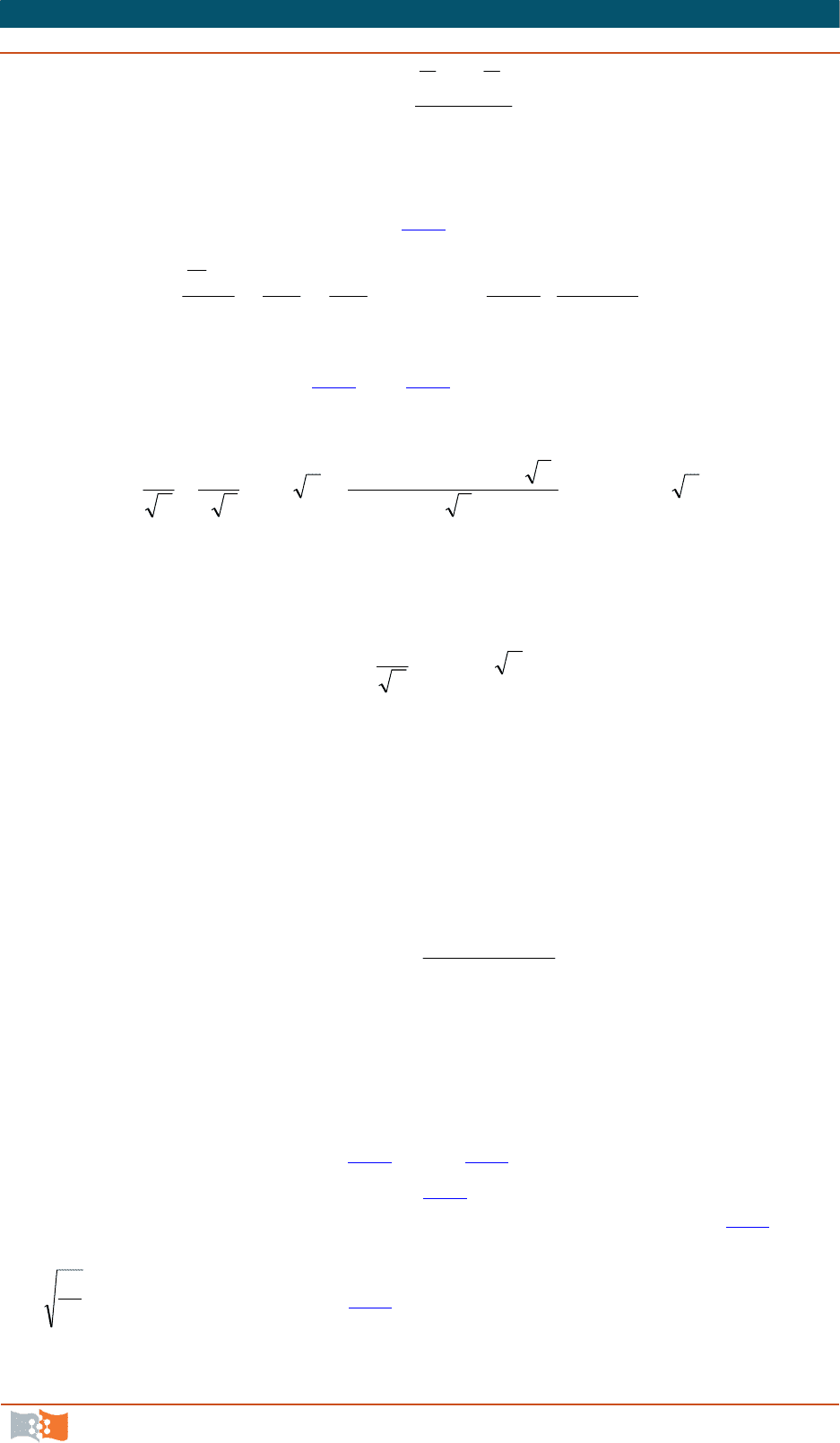
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 188

.75,3

срmax







(8.44)

Это соотношение хорошо согласуется с опытными данными.

Обратимся снова к уравнению (8.41

) и запишем его в следующей форме:

5,5

lg75,5

ср0срср

max























ср

Используя равенства (8.42

) и (8.44) и учитывая, что

Re/2

ср0



VR

, мо-

жем записать









.13,1Relg03,2

24lg75,575,35,5

Relg

75,51









Лучшее согласие с опытными данными дает формула Никурадзе, в ко-

торой коэффициенты определены эмпирическим путем:





8,0Relg2





. (8.45)

Эта полуэмпирическая формула выражает универсальный логарифми-

ческий закон сопротивления для гладких труб и справедлива для любых чи-

сел Рейнольдса, отвечающих турбулентному движению. Недостаток этой

формулы заключается в том, что в ней зависимость от числа Re выражена в

неявной форме и поэтому решать ее приходится методом последовательных

приближений. Этого недостатка лишена эмпирическая формула Конакова



5,1Relg8,1





(8.46)

также справедливая для широкого диапазона чисел Рейнольдса.

Приведенные формулы позволяют провести полный расчёт турбулент-

ного движения жидкости в круглой трубе. Сначала по заданному расходу и

диаметру трубы определяют среднюю скорость и число Рейнольдса

 /Re

ср

. Затем по формуле (8.45) или (8.46) находят коэффициент сопро-

тивления



. После этого по формуле (8.11) определяют само сопротивление,

т. е. перепад давления на заданном участке трубы, и по формуле (8.14

) – на-

пряжение трения на стенке



, а следовательно, и динамическую скорость









. Наконец, по формуле (8.40) находят распределение скоростей по се-

чению трубы.

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.3. Турбулентное движение жидкости в гладкой цилиндрической трубе



Гидрогазодинамика. Учеб. пособие 189

Наряду с логарифмическими формулами для коэффициента сопротив-

ления трубы и для распределения скорости при турбулентном движении су-

ществуют еще и степенные, однако они менее универсальны. Так, широкое

применение получила эмпирическая формула Блазиуса

3164,0

25,0



(8.47)

пригодная при значениях числа Рейнольдса, не превышающих 1·10

Этой формуле отвечает следующее степенное выражение для распре-

деления скорости по сечению трубы, область применения которого также ог-

раничивается указанным значением числа Рейнольдса:

7/1

57,8



















, (8.48)

где x

– расстояние от стенки трубы.

Это уравнение известно под названием закона Блазиуса, или закона

корня седьмой степени.

Для максимальной скорости на оси трубы







можно записать

.57,8

7/1

0max



















(8.49)

Из равенств (8.48) и (8.49) получаем

7/1

max















(8.50)

Все формулы, полученные в предыдущем параграфе, относятся к тру-

бам с гладкой поверхностью. В действительности же поверхность трубы все-

гда имеет некоторую шероховатость. По форме неровностей, образующихся

на поверхности, различают шероховатость зубчатую и волнистую. Однако в

качестве объекта экспериментального исследования обычно прибегают к

трубам с искусственной, или т. н. «зернистой» шероховатостью, которая соз-

дается путем приклеивания к ст

енке трубы сплошного и равномерного слоя

песка с определенной средней величиной зерна.

В качестве обобщенной характеристики шероховатости трубы служит

отношение ее абсолютной шероховатости, под которой понимается средняя вы-

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ

8.4. Влияние шероховатости стенки трубы на коэффициент сопротивления



Гидрогазодинамика. Учеб. пособие 190

сота бугорков шероховатости и которую обозначают через k, к радиусу трубы

R0:

/ Rkk 

. Величину k называют относительной шероховатостью трубы.

Величину абсолютной шероховатости k для труб, изготовленных из

различных материалов, см. в таблице (с. 183).

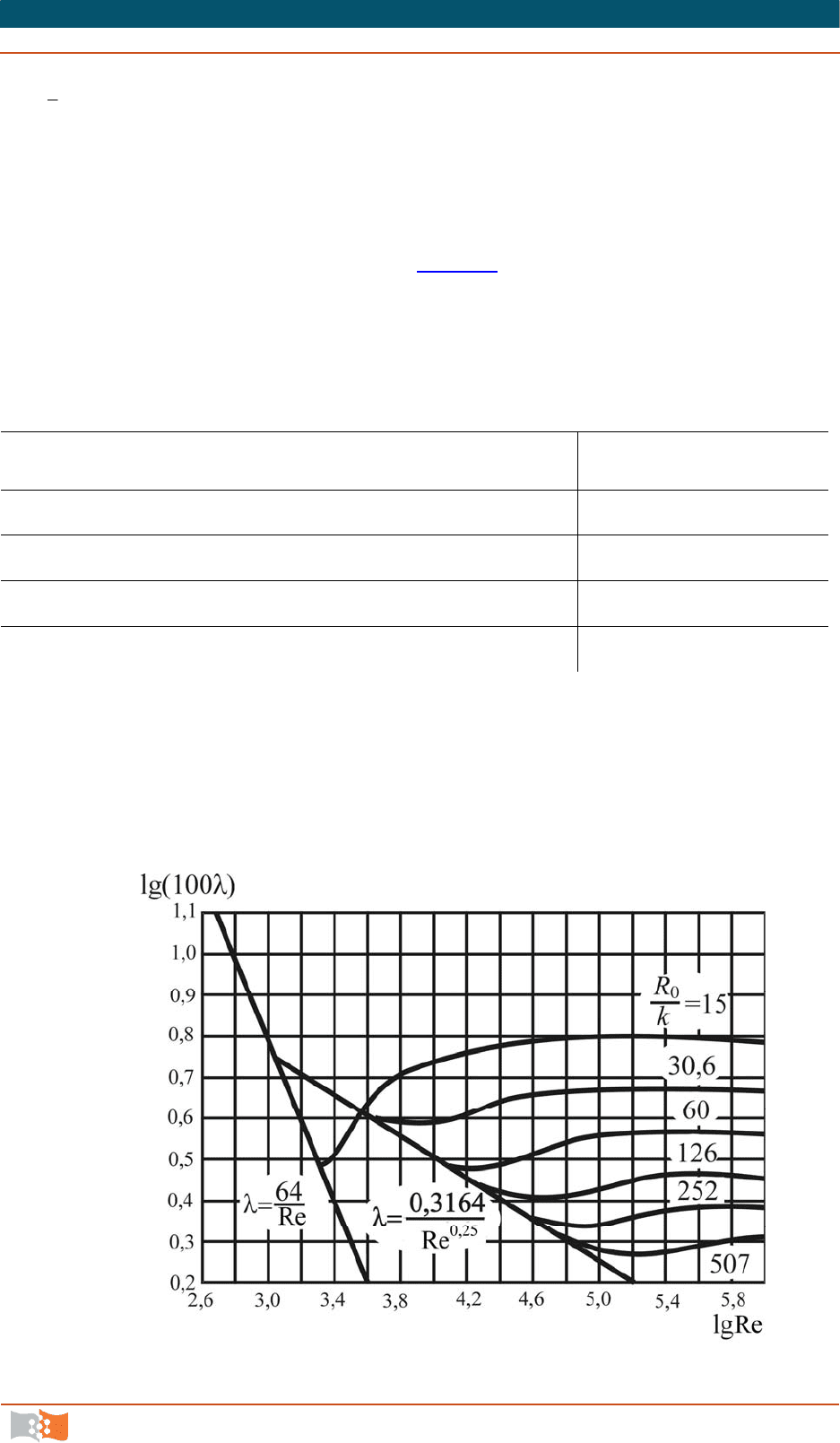
Обширное исследование влияния шероховатости зернистого типа на

коэффициент сопротивления круглых труб было выполнено Никурадзе. Ре-

зультаты его опытов представлены на рис. 8.6

в виде кривых зависимости ко-

эффициента сопротивления



от числа





/Re

ср

при различных значениях

kR /

 величины, обратной относительной шероховатости.

Таблица

Трубы

10 ,k 

мм

Стеклянные

0,2

0,8

Новые тянутые из латуни, свинца, меди

0,2

1,0

Железные новые

50

Чугунные новые

100

200

По характеру зависимости



от Re график можно разбить на три об-

ласти. Первая область, отвечающая значениям Re



2300 (lgRe



3,3), от-

носится к ламинарному движению, при котором коэффициент сопротивле-

ния не зависит от шероховатости трубы и остается таким же, как для глад-

ких труб.