Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА
7.6. Проектирование сопла Лаваля
Гидрогазодинамика. Учеб. пособие 171
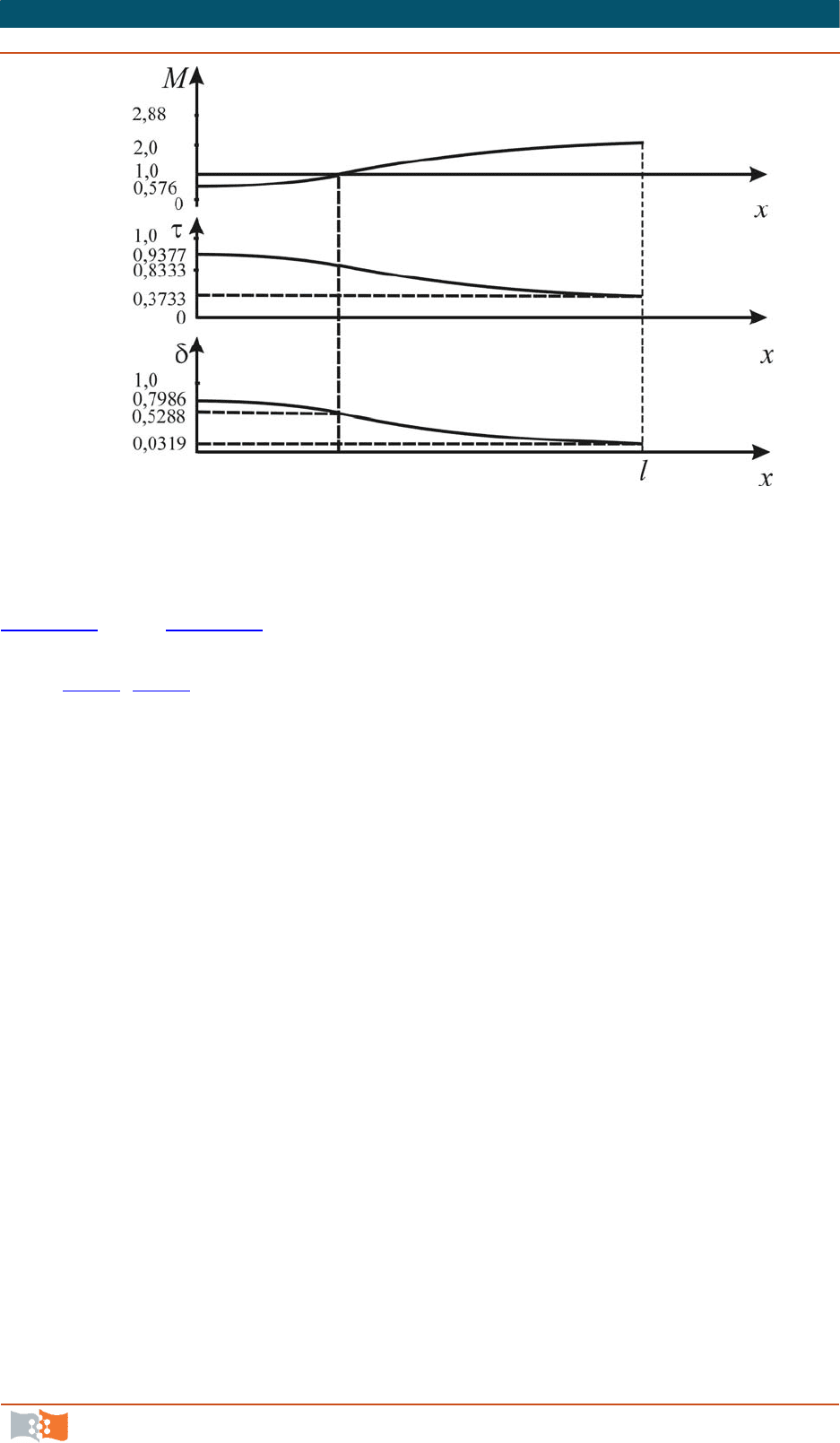
Рис. 7.16
Графическое изображение расчетного сопла Лаваля показано на
рис. 7.15
, а на рис. 7.16 представлено соответствующее изменение гидроди-
намических функций вдоль сопла (построение проведено по данным приме-
ров в п. 7.3
, п. 7.4).

Гидрогазодинамика. Учеб. пособие 172
8
8
.
.
В
В
И
И
Ж
Ж
Е
Е
Н
Н
И
И
Е
Е
В
В
Я
Я
З
З
К
К
О
О
Й
Й
Н
Н
Е
Е
С
С
Ж
Ж
И
И
М
М
А
А
Е
Е
М
М
О
О
Й
Й
Ж
Ж
И
И
Д
Д
К
К
О
О
С
С
Т
Т
И
И
В
В
Т
Т
Р
Р
У
У
Б
Б
А
А
Х
Х
8
8
.
.
1
1
.
.
У
У
с
с
т
т
а
а
н
н
о
о
в
в
и
и
в
в
ш
ш
е
е
е
е
с
с
я
я
л
л
а
а
м
м
и
и
н
н
а
а
р
р
н
н
о
о
е
е
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
е
е
в
в
я
я
з
з
к
к
о
о
й
й
н
н
е
е
с
с
ж
ж
и
и
м
м
а
а
е
е
м
м
о
о
й
й
ж
ж
и
и
д
д
к
к
о
о
с
с
т
т
и
и
в
в
ц
ц
и
и
л
л
и
и
н
н
д
д
р
р
и
и
ч
ч
е
е
с
с
к
к
о
о
й
й
т
т
р
р
у
у
б
б
е
е
Установившееся ламинарное движение несжимаемой вязкой жидкости
через цилиндрическую трубу является одним из случаев, для которого можно
получить простое и точное решение уравнений Навье Стокса. Будем рас-
сматривать движение жидкости на участке трубы, достаточно удаленном от
входного сечения, чтобы ламинарный режим движения можно было считать
стабилизированным.
Ось х
1
, вдоль которой направлен поток, совместим с осью трубы. Ком-
поненты скорости V
2
и V
3
равны нулю. Для трубы, расположенной горизон-
тально, массовая сила (сила тяжести) также равна нулю.
Перечисленные упрощения позволяют свести уравнения Навье Сто-
кса и уравнение неразрывности к следующей системе уравнений:
.0
;
1
0
;
1
0
;
1
1
1
3
2
2
3
1
2
2
2
1
2
2
1
1
2
11
1
1
x
V
x
P
x
P
x
V
x
V
x
V
x
P
x
V
V
(8.1)
Из этих уравнений непосредственно следует, что скорость является
функцией только координат х
2
и х
3
, а давление зависит только от координаты х
1
.
Это означает, что во всех поперечных сечениях трубы распределения скоро-
стей одинаковы, а поля давлений однородны.
Таким образом, система уравнений (8.1
) сводится к одному:

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.1. Установившееся ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
Гидрогазодинамика. Учеб. пособие 173
1
2
3
1
2
2
2
1
2
1
dx
dP
x
V
x
V
. (8.2)
Поскольку левая часть равенства (8.2
) является функцией только х
2
и х
3
,
а правая – функцией только х
1
, то ввиду независимости координат друг от
друга существование этого равенства возможно лишь в том случае, когда ка-
ждая его часть представляет постоянную величину.
Обозначив через
P
падение давления на участке трубы длиною
l
,
можем написать
l
P
dx
dP
const
1
.
Величина
lP
представляет движущий перепад давления на единицу
длины, идущий на преодоление сил сопротивления, обусловленных трением.
Распределение скоростей по сечению трубы симметрично относитель-
но ее оси. Поэтому целесообразно лапласиан от
1
V
в уравнении (8.2) выразить
в полярных координатах:
.
11
2
1
2
2
1
2
1
2
1
2
V
RR
V
RR
V
V
Но в силу осевой симметрии
0
2
1
2
V
. Следовательно,
dR
dV
R
dR
d
RdR
dV
RdR
V
V
11
2
1
2
1
2
11
.
Теперь вместо (8.2
) будем иметь (подстрочный индекс «1» в дальней-
шем опускаем)
l
P
dR
dV
R
dR
d
R
1
. (8.3)
Первое интегрирование дает
.
2
1
2
CR
l
P
dR
dV
R
В результате повторного интегрирования получим
.ln
4
21
2
CRCR
l
P
V
(8.4)
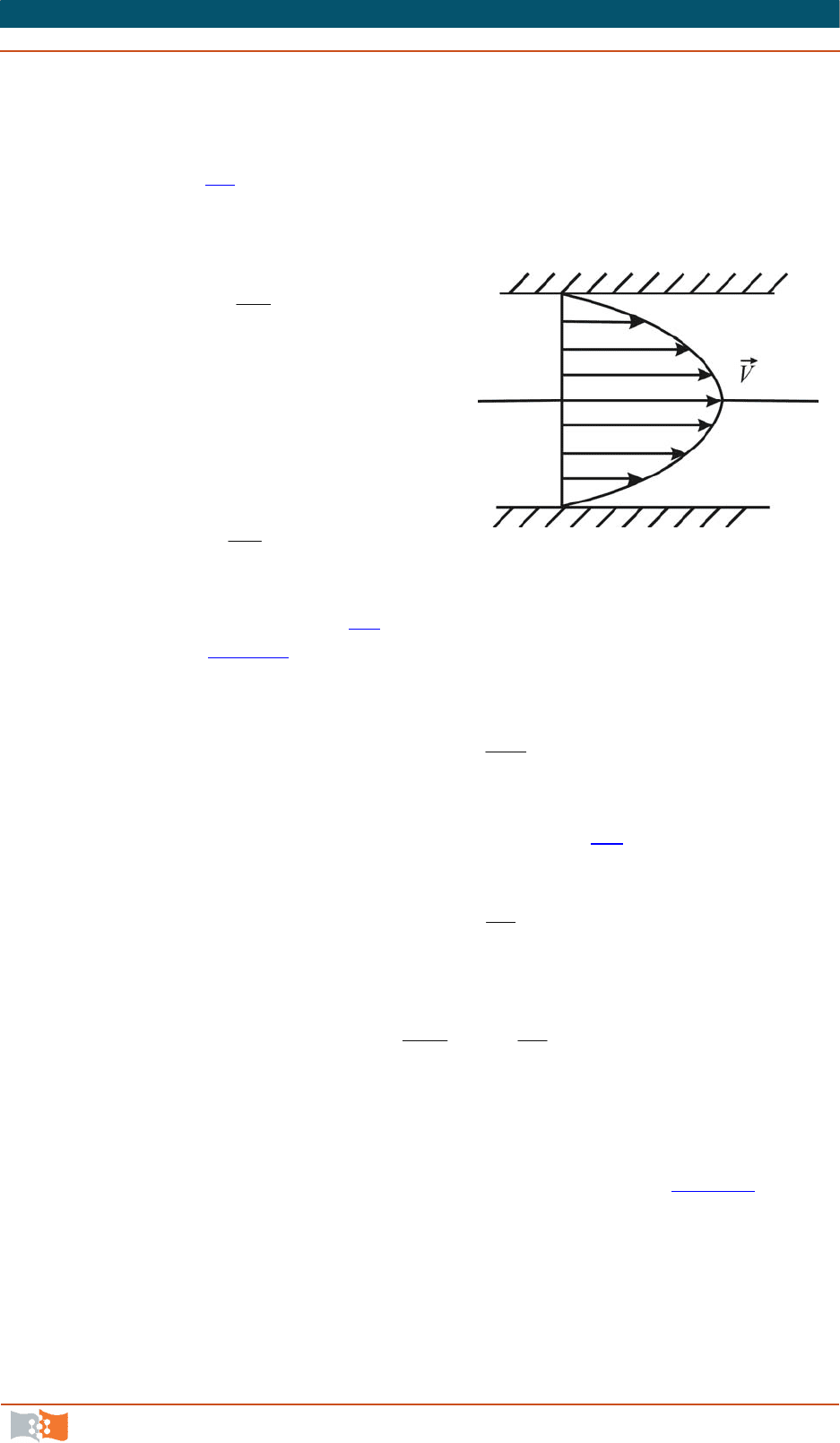
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.1. Установившееся ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
Гидрогазодинамика. Учеб. пособие 174
Произвольная постоянная C
1
должна быть положена равной нулю. Это
вытекает из условия, что при R = 0 (т. е. на оси трубы) скорость должна
иметь конечное значение. При
0
1
C
скорость на оси трубы приняла бы, со-
гласно уравнению (8.4
), бесконечно большое значение. Следовательно, C
1
= 0.
Постоянную C
2
находим из граничного условия на поверхности трубы:
R = R
0
(R
0
– радиус трубы);
V
= 0. Имеем
2
0
2
4
R
l
P
Ñ
.
Таким образом, получим сле-
дующее выражение для распределения
скоростей по сечению цилиндрической
трубы:
.
4
22
0
RR
l
P
V
(8.5)
Как видно из уравнения (8.5
), это распределение подчиняется парабо-
лическому закону (рис. 8.1
).
Максимальная скорость V
max
достигается на оси трубы, т. е. при R = 0:
2
0max
4
R
l
P
V
. (8.6)
Пользуясь этим выражением, можно уравнение (8.5
) переписать в виде
,1
2
0
max
R
R
VV
или
.1
2
0
max
R
R
V
V
(8.7)
Зная распределение скоростей, можно определить секундный объем-
ный расход жидкости через поперечное сечение трубы.
Для элементарного расхода через кольцевую полоску (рис. 8.2
) шири-
ною dR и площадью сечения
RdRdS
2
можем написать
.2 RdRVdQ
Рис. 8.1

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.1. Установившееся ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
Гидрогазодинамика. Учеб. пособие 175
Чтобы найти расход через все се-
чение трубы, нужно это уравнение про-
интегрировать, используя выражение
(8.5
) для распределения скоростей,
.
2
2
00
0
22
0
0
RdRRR
l
P
RdRVQ
RR
Отсюда
.
8
4
0
R
l
P
Q
(8.8)
Уравнение (8.8
) выражает закон Пуазейля, согласно которому объем
несжимаемой жидкости, проходящий в единицу времени через сечение ци-
линдрической трубы при ламинарном движении, пропорционален перепаду
давления на единицу длины трубы и четвертой степени ее радиуса и обратно
пропорционален динамическому коэффициенту вязкости жидкости.
Разделив расход жидкости на площадь сечения трубы
2
0
RS
, получим
среднюю скорость по сечению трубы
4
2
0
0
2
0
.
8
8
ср
PR
QP
VR
Sl
lR
(8.9)
Из сравнения выражений (8.6
) и (8.9) следует, что при ламинарном
движении в цилиндрической трубе максимальная скорость на оси трубы
вдвое больше средней скорости по сечению, т. е.
.2
срmax
VV
(8.10)
Перейдем теперь к определению величины гидравлического сопротив-
ления при движении жидкости в трубе. Для установившегося движения ме-
рой этой величины служит перепад давления на данном участке трубы.
Обычно величину
P
выражают через скоростной напор, определенный по
средней скорости потока; в частности, для цилиндрической трубы
.
2
2
ср
V
d
l
P
(8.11)
Здесь l длина рассматриваемого участка трубы; d – диаметр участка
трубы;
– безразмерный коэффициент пропорциональности, именуемый ко-
эффициентом сопротивления.
Рис. 8.2

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.1. Установившееся ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
Гидрогазодинамика. Учеб. пособие 176
В общем случае коэффициент сопротивления зависит как от природы
жидкости и скорости ее движения, так и от состояния поверхности трубы
(т. е. от ее шероховатости). В рассматриваемом здесь случае ламинарного
движения, т. е. движения, совершающегося при
кр
ReRe
, шероховатость сте-
нок не оказывает влияния на коэффициент сопротивления. Значение этой ве-
личины может быть найдено исключительно расчетным путем. Для этой цели
воспользуемся уравнениями (8.11
) и (8.9), выразив последнее относительно
P
:
.
328
2
22
0
ср
2
ср
d
lV
R
lVV
d
l
P
ср
Отсюда находим
dV
ср
64
,
или
ср
Re
64
. (8.12)
Это уравнение выражает закон сопротивления для ламинарного движе-
ния вязкой жидкости в цилиндрической трубе.
Зная коэффициент сопротивления и среднюю скорость, вычисляемую
по заданному расходу, можно по формуле (8.11
) найти перепад давления. В
свою очередь, по перепаду давления можно определить напряжение трения
на стенке трубы. Воспользуемся условием равновесия для объема жидкости,
заключенного между двумя выделенными сечениями трубы (рис. 8.3
). Пере-
пад давления, приложенного к сечению трубы с площадью
2
0
R
, должен
уравновешиваться силой трения, действующей на боковую поверхность рас-
сматриваемого участка
l
трубы, т. е.
lRRP
w 0
2
0
2
. Отсюда
.
2
0
R
l
P
w
(8.13)
Таким образом, напряжение трения на стенке цилиндрической трубы
равно перепаду давления на участке трубы длиною, равной половине радиуса.

8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.1. Установившееся ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
Гидрогазодинамика. Учеб. пособие 177
Рис. 8.3
Подставив в выражение (8.13
) значение
P
из формулы (8.11), полу-
чим зависимость между напряжением трения на стенке и коэффициентом со-
противления
.
8
2
ср
V
w
(8.14)
Важно отметить, что выражение (8.13
) справедливо для любого режима
движения, как ламинарного, так и турбулентного, поскольку оно вытекает из
общего условия равновесия сил, приложенных к движущейся жидкости. То
же самое следует сказать и о формуле (8.14
), основанной на использовании
общей зависимости (8.11
).
8
8
.
.
2
2
.
.
О
О
с
с
н
н
о
о
в
в
н
н
ы
ы
е
е
э
э
л
л
е
е
м
м
е
е
н
н
т
т
ы
ы
т
т
е
е
о
о
р
р
и
и
и
и
т
т
у
у
р
р
б
б
у
у
л
л
е
е
н
н
т
т
н
н
о
о
г
г
о
о
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
Выше было установлено, что при
êð
ReRe
ламинарный режим движе-
ния жидкости уступает место турбулентному. Этот переход связан с возрас-
танием инерционных сил, действующих на поток возмущающим образом и
усиливающих неупорядоченность движения, по сравнению с силами вязкого
сопротивления, которые способствуют сохранению упорядоченной формы
движения. По характеру перемещения отдельных частиц жидкости турбу-
лентный поток является всегда нестационарным, даже в том случае, когда
наблюдаемая скорость потока, определяемая, например, как средняя по рас-
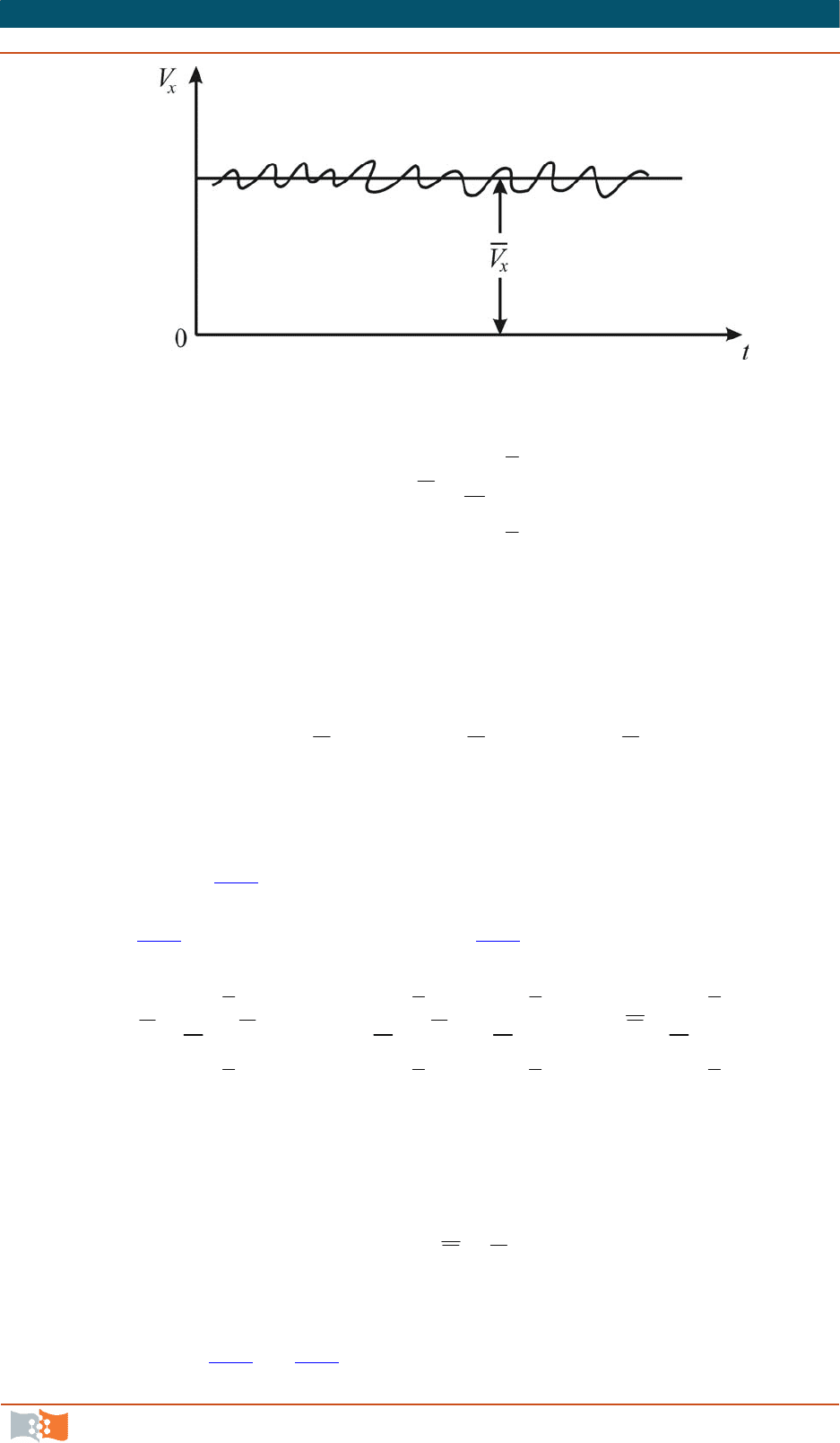
ходу, остается во времени постоянной. В этом случае скорость в каждой точ-
ке потока беспорядочно пульсирует около некоторого среднего значения
(рис. 8.4
).
Для описания турбулентного потока вместо действительных (мгновен-
ных) значений скорости и давления пользуются осредненными во времени
значениями этих величин. Например, составляющая осредненной скорости в
направлении оси х
1
в некоторой точке потока определяется соотношением
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.2. Основные элементы теории турбулентного движения
Гидрогазодинамика. Учеб. пособие 178
Рис. 8.4
,
1
2
2
11
dtV
T
V
T
t
T
t
(8.15)
где V
1
– мгновенная скорость, зависящая от времени; Т – период осред-
нения.
Действительное значение скорости может быть представлено как сум-
ма осредненной и пульсационной величины, т. е.
;
111
VVV
;
222
VVV
333
VVV
. (8.16)
Период осреднения Т должен выбираться достаточно большим по
сравнению с периодом пульсации.
Из равенств (8.16
) следует, что осредненные пульсационные скорости
должны быть равны нулю. Действительно, подставив под знак интеграла в
выражении (8.15
) значение
1
V
из равенства (8.16), получим
2
2
2
2
2
2
2
2
.
111
1
1111111
T
t
T
t
T
t
T
t
T
t
T
t
T
t
T
t
dtV
T
VdtV
T
dtV
T
dtVV
T
V
(8.17)
Очевидно, что при достаточно большом значении периода осреднения Т
повторное осреднение данной величины не должно приводить к ее измене-
нию, т. е.
.
11
VV
(8.18)
Из равенств (8.17
) и (8.18) следует, что
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.2. Основные элементы теории турбулентного движения
Гидрогазодинамика. Учеб. пособие 179
.VdtV
T
T
t
T
t
0
1
1
2
2
1
(8.19)
Если осредненные величины оказываются для разных последователь-
ных моментов времени постоянными, то такое турбулентное движение назы-
вают квазистационарным, а отвечающее ему осредненное движение ста-
ционарным.
Подставив в уравнения Навье Стокса и в уравнение неразрывности
вместо компонентов скорости их выражения через осредненные и пульсаци-
онные величины, можно получить систему уравнений осредненного движе-
ния (массовую силу полагаем отсутствующей):
.0
;
;
;
3
3
2
1
1
1
2
3
3
32
2
31
1
3
2
33
3
3
2
3
2
1
3
1
3
31
3
2
2
2
21
1
2
2
23
2
3
2
2
2
1
2
1
2
31
3
21
2
2
1
1
1
2
13
1
3
2
1
2
1
1
1
1
x
V
x
V
x
V
V
x
VV
x
VV
x
V
x
P
x
V
V
x
V
V
x
V
V
t
V
VV
x
V
x
VV
x
V
x
P
x
V
V
x
V
V
x
V
V
t
V
VV
x
VV
x
V
x
V
x
P
x
V
V
x
V
V
x
V
V
t
V
Эти уравнения получили название уравнений Рейнольдса. По сравне-
нию с уравнениями Навье Стокса каждое из уравнений движения системы
(8.20)
8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
8.2. Основные элементы теории турбулентного движения
Гидрогазодинамика. Учеб. пособие 180
(8.20) включает еще три дополнительных члена. Физическое содержание этих
членов становится очевидным при сопоставлении уравнений (8.20
) с уравне-
ниями движения в напряжениях.
Чтобы из этих уравнений получить уравнения (8.20
), к нормальным и
касательным напряжениям, обусловленным обычной вязкостью, следует до-
бавить нормальные и касательные напряжения, возникающие под влиянием
пульсации скорости:
2
1
1
1
11
2 V
x
V
PP
;
;
21
1
2
2
1
2112
VV
x
V
x
V
PP
……………………………………………………………;
……………………………………………………………;
Величины
;
2
111
VP
;
2
222
VP
;
2
333
VP
;
2112
VVP
;
3113
VVP
3223
VVP
носят название турбулентных напряжений.
Совокупность этих величин образует, подобно вязким напряжениям,
симметричный тензор турбулентных напряжений:
2
33231
32
2
221
31
21
2
1
VVVVV
VV
VVV
VV
VVV
(8.21)
Таким образом, дополнительные члены в уравнениях (8.20
), о которых
идет речь, имеют смысл добавочных составляющих нормальных и тангенци-
альных сил, обусловленных турбулентными напряжениями.
Чтобы систему уравнений (8.20
) сделать замкнутой, необходимо дополнить
ее шестью уравнениями, связывающими турбулентные напряжения скорости.
Для описания касательных турбулентных напряжений можно восполь-
зоваться уравнением, аналогичным по форме уравнению (1.8
), выражающему
закон Ньютона для напряжения, обусловленного молекулярной вязкостью.
Так, например, для плоскопараллельного движения, в котором скорость
1
V
является функцией одного
2
x
, можем написать
.
2
1
2112
dx
Vd
AVVP
(8.22)
Величину
A
, получившую название коэффициента турбулентного
обмена, можно рассматривать как коэффициент кажущейся вязкости, обу-
словленной макроскопическим переносом количества движения конечными
