Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

Подождите немного. Документ загружается.



Гидрогазодинамика. Учеб. пособие 141

Если при движении газа возникают разности давлений, небольшие по

сравнению с абсолютным давлением газа, то изменения объема получаются

столь малыми, что такие потоки газа можно считать в первом приближении

несжимаемыми.

При движении газа большие разности давлений и связанные с ними зна-

чительные изменения объема возникают в основном в следующих случаях:

1) когда п

ространство, за

нятое газом, находящимся под действием силы

тяжести, имеет большую протяженность в высоту (движение масс воздуха в

свободной атмосфере – предмет рассмотрения динамической метеорологии);

2) когда в потоке газа имеют место большие скорости (течение через

отверстия и в каналах, движение тел в газе с большой скоростью рассматри-

ваются в рамках газовой динамики);

3) когда движение га

а связано с большими ускорениями (случаи быст-

рых колебаний в газе (такие движения рассматриваются в акустике), при взрыв-

ных волнах и быстром открытии или закрытии задвижек в трубопроводах).

Во всех этих случаях чрезвычайно важную роль играет скорость, с ко-

торой в массе газа распространяются возмущения давления. Величина этой

скорости зависит т

лько от термодинамического состояния газа, является ха-

рактерной для данного газа и играет важную роль для выяснения особенно-

стей движения газа – скорость распространения малых возмущений (напри-

мер малых сжатий) по газу равносильна скорости распространения звука.

Поэтому подробно остановимся прежде всего на этом процессе.

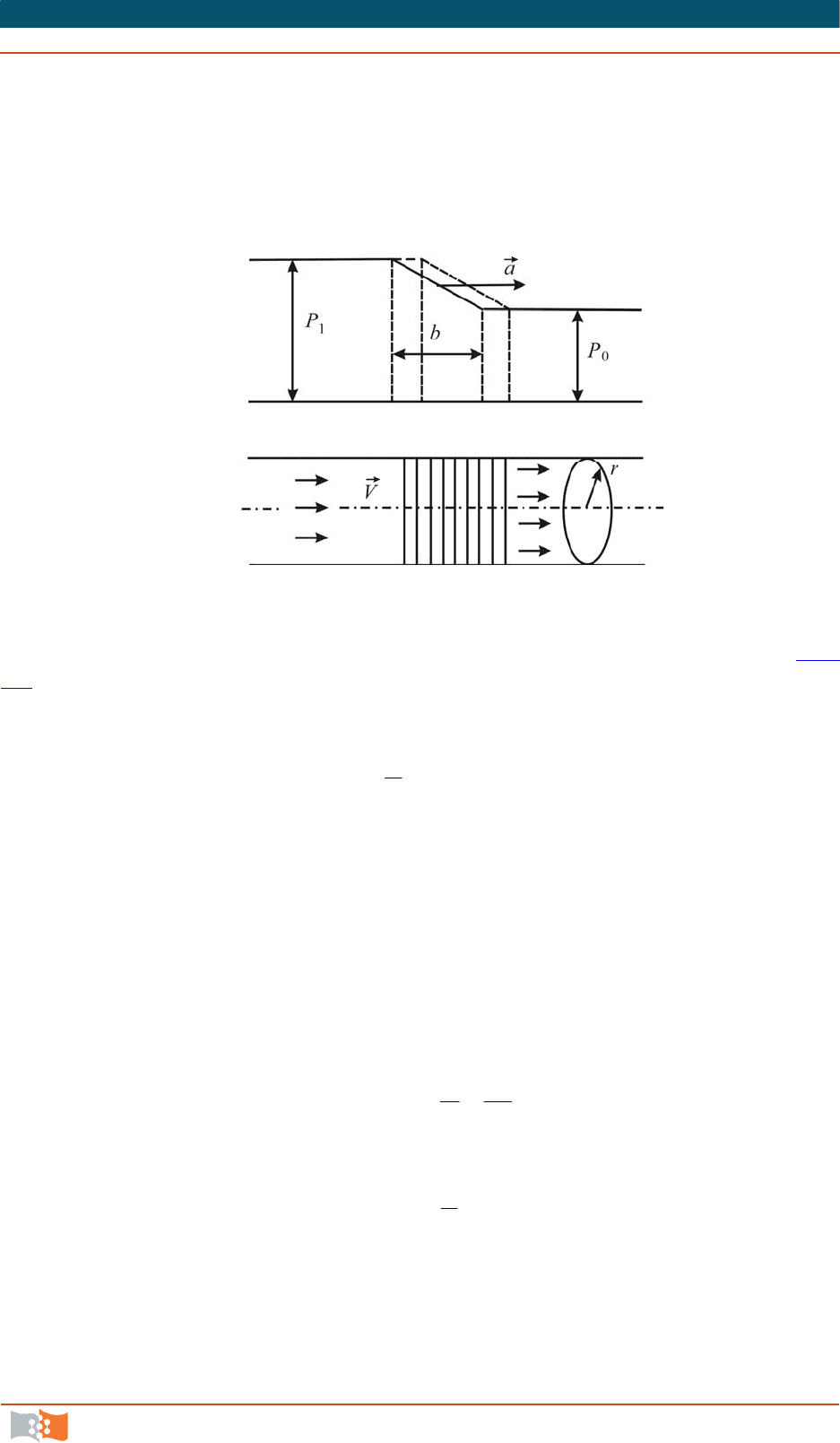
Пусть в покоящейся массе газа, заключенной в широкой трубе, к.-л.

образом (например, движением поршня) создано повышение давления. Это

повышение давления начинает распространяться вправо, как это показано

схематически на рис. 7.1

. Предположим, что возникшее распределение дав-

ления перемещается, не изменяя формы, со скоростью a. Так как газ при этом

сжимается, то та его часть, через которую повышение давления уже про-

изошло, должна обладать некоторой скоростью V. Примем, что P

 P

, а следо-

вательно, и





малы.

7. ГАЗОВАЯ ДИНАМИКА

7.1. Скорость распространения малых возмущений в идеальном газе. Скорость звука



Гидрогазодинамика. Учеб. пособие 142

Тогда задача о распространении в газе малых возмущений может быть

сформулирована так: в покоящемся идеальном и совершенном газе создают-

ся весьма малые возмущения скоростей, давлений или плотности, причем

возникающее вследствие этого движение является одномерным и баротроп-

ным, зависящим только от координаты, совпадающей с осью трубы, и време-

ни; требуется разыскать элементы возмущенного движения.

Рис. 7.1

Относительно явлений, которые происходят в области шириной

(рис.

7.1) можно сказать следующее: за время

àb /





, когда область

проходит

через к.-н. место массы газа, плотность в нем увеличивается от



до



. При-

ращение массы газа в единицу времени в переходной области





aFm











где



площадь сечения объема

. Оно вызвано тем, что в переход-

ную область втекает из области сгущения масса газа



. Вследствие не-

разрывности течения, приравнивая обе массы, получаем





011











. (7.1)

Внутри переходной области скорость увеличивается (за промежуток

времени



) от 0 до

, тогда среднее ускорение

VaV





. (7.2)

Масса, которой сообщается ускорение,





, (7.3)

где



средняя плотность. Результирующая сила равна



PPF



, то-

гда из основного уравнения динамики имеем

PPVa







. (7.4)

7. ГАЗОВАЯ ДИНАМИКА

7.1. Скорость распространения малых возмущений в идеальном газе. Скорость звука



Гидрогазодинамика. Учеб. пособие 143

Заменив в левой части уравнения (7.2)



на



(допуская при этом не-

существенную погрешность) и разделив уравнение (7.4

) на (7.1), получим







. (7.5)

Правая часть этого уравнения зависит только от закона сжатия газа и

существенно положительна, т. к. плотность совершенного газа растет с дав-

лением; можем ввести обозначения





. (7.6)

Таким образом, если изменения давления в газе малы, то скорость их

распространения не зависит ни от их величины, ни от ширины переходной

зоны и определяется только законом сжатия газа. Отсюда следует, что ско-

рость распространения колебаний давления не изменится, если будут следо-

вать друг за другом различные по знаку изменения давления, ли

шь бы они

были мал

ыми. К числу наиболее широко наблюдаемых явлений распростра-

нения малых возмущений в жидкостях и газах относится распространение

звука, представляющее, как известно, распространение волн слабого разре-

жения и сжатия. В связи с этим величину а называют скоростью звука.

При изотермическом процессе распространения звука, согласно урав-

нению состояния, его скорость выраж

ется формулой Ньютона



a 

. (7.7)

Если процесс распространения звука происходит без теплообмена с ок-

ружающей средой, имеем адиабатический процесс сжатия









kkC

;

адиабатическая скорость звука будет определяться формулой, предло-

женной Лапласом,





. (7.8)

Применяя формулу Клайперона, можем переписать (7.8

) в виде

kRTa 

. (7.9)

Отсюда следует, что скорость распространения малых возмущений в

совершенном газе зависит только от температуры и физических свойств газа.

Подставив в (7.9

) значение газовой постоянной

7. ГАЗОВАЯ ДИНАМИКА

7.1. Скорость распространения малых возмущений в идеальном газе. Скорость звука



Гидрогазодинамика. Учеб. пособие 144

град

848





мg

получим





кgТ

848

Для воздуха при

4,1k

96,28





81,9



Ta 1,20

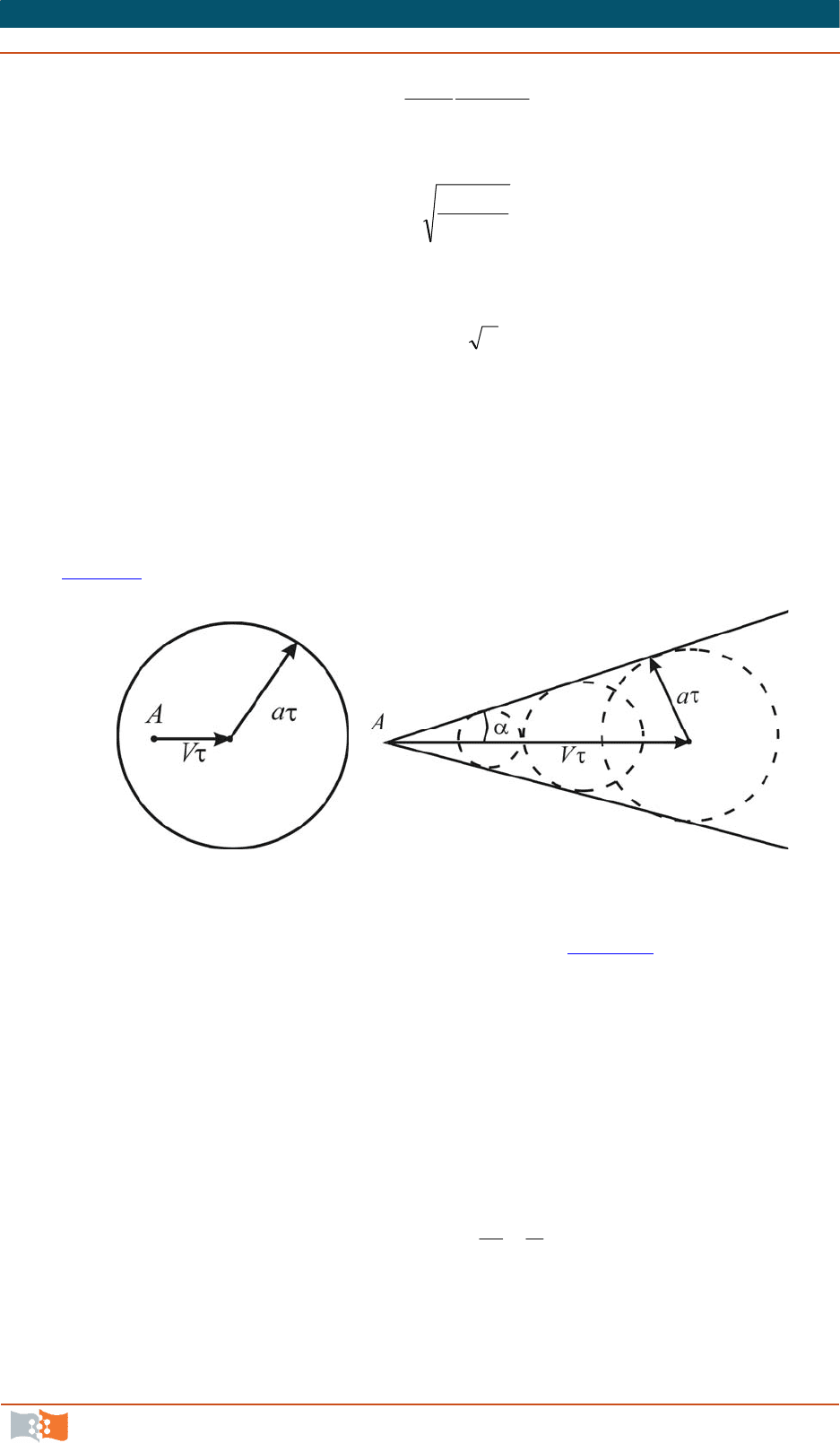
Возмущения, исходящие от неподвижного источника в покоящемся газе,

распространяются в виде концентрических сферических волн, фронт которых

представляет собой тонкий слабоуплотненный слой. При движении источника

возмущений (например твердого тела) относительно неподвижного газа вели-

чина

является критерием движения (если



, движение дозвуковое, если

 – сверхзвуковое). В случае a



возмущения опережают движущееся

тело (рис. 7.2

), распространяясь вперед с относительной скоростью а  V.

Рис. 7.2 Рис. 7.3

Если скорость тела больше скорости звука (рис. 7.3), в направлении

движения оно все время обгоняет генерируемые им возмущения. В этом слу-

чае шаровые волны возмущений заполняют только конус, расходящийся вниз

по потоку и имеющий свою вершину в точке

. Пространство вне конуса ос-

тается совершенно свободным от влияния источника возмущения. Поверх-

ность конуса представляет собой фронт волны возмущений. При переходе

через него состояние газа изменяется скачкообразно.

Угол между образующей конуса и его осью, совпадающей с направле-

нием течения, определяется соотношением





sin

(7.10)

и называется углом Маха.

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА



Гидрогазодинамика. Учеб. пособие 145

Многочисленные опыты показывают, что переход сверхзвукового те-

чения в дозвуковое происходит скачкообразно. Простейшим примером прерыв-

ного уплотнения является прямой установившийся скачок уплотнения, впервые

рассмотренный Стодолой и для идеального газа объясненный Риманом.

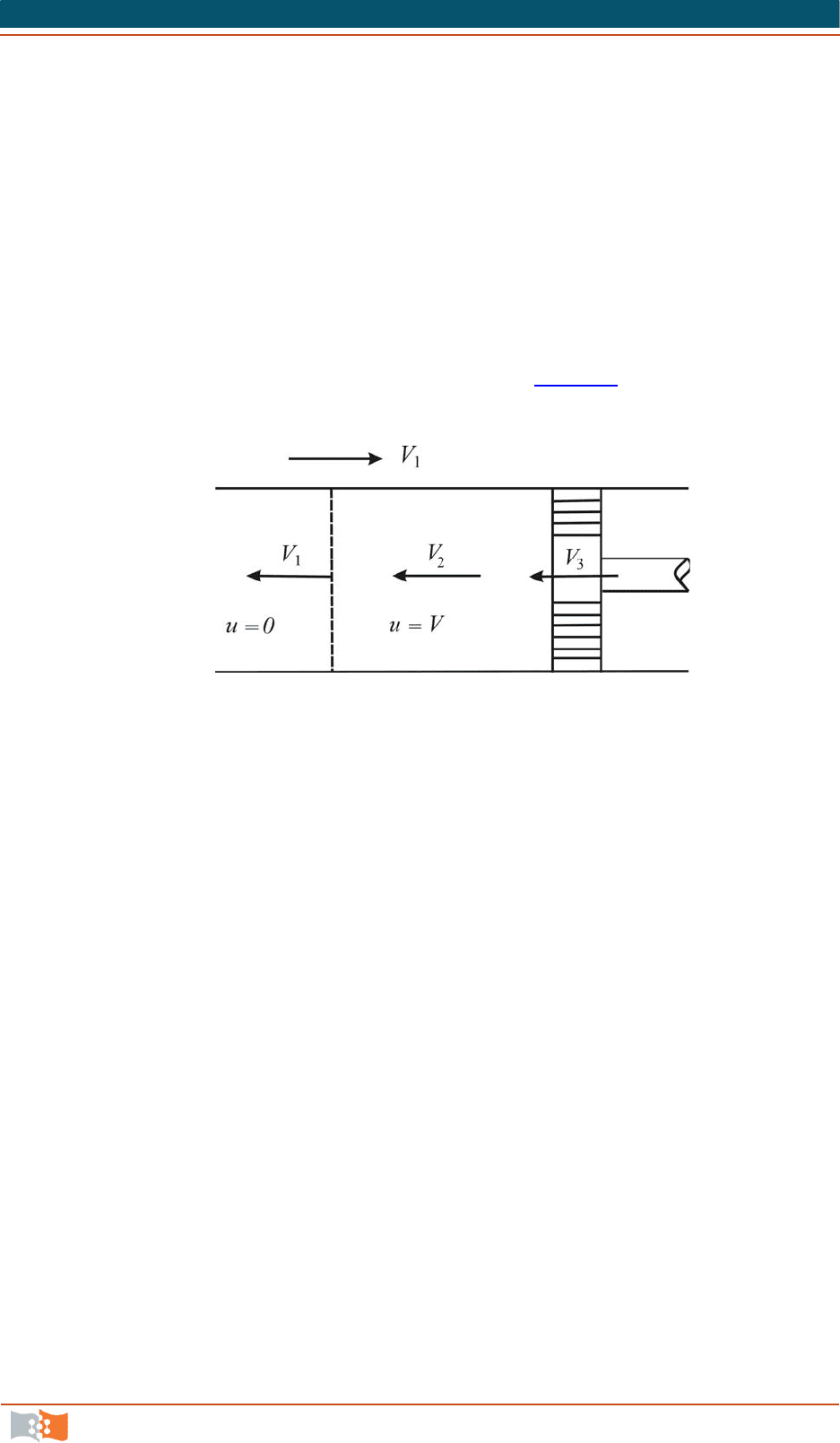
Представим себе бесконечную цилиндрическую теплоизолированную

трубу, вдоль которой перемещается поршень. В начальный момент времени

неподвижный поршень мгновенно приобретает скорость

и перемещается с

этой скоростью влево, сжимая перед собой газ (рис. 7.4

). Возникающее при

этом возмущение газа (сжатие) будет распространяться по трубе.

Рис. 7.4

Если рассматривать движение газа в данном сечении (перпендикуляр-

ном оси трубы) как относительное в системе координат, движущейся посту-

пательно и равномерно со скоростью газа в смежном сечении, можем в такой

галилеевой системе применить теорию распространения малых возмущений.

Это позволит утверждать, что скорость распространения возмущений в каж-

дом сечении равна местной скорости звука. Таки

м образом, во

змущения,

создаваемые поршнем, можно рассматривать как совокупность звуковых

волн, следующих друг за другом. Но в рассматриваемом адиабатическом и

изэнтропическом движении сжатие газа сопровождается его нагревом, а ско-

рость звука возрастает с температурой. Следовательно, каждая последующая

волна относительно невозмущенного газа будет перемещаться быстрее, чем

предыдущая. Волны будут догонять друг друга, складываться и образовывать

одну мощную волну сжат

ия с усто

йчивым плоским фронтом, называемую

ударной волной, или прямым скачком уплотнения.

При движении поршня за ним образуется разрежение, которое будет

распространяться вправо также волновым образом. Но в этом случае волны

уже не будут догонять друг друга, т. к. последующая волна пойдет по газу,

охлажденному предыдущей волной, и скорость распространения п

следую-

щей волны будет меньше скорости предыдущей. Поэтому волны разрежения

не образовывают ударных волн.

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА

7.2. Теория прямого скачка уплотнения



Гидрогазодинамика. Учеб. пособие 146

Из описания механизма развития ударной волны сжатия следует, что,

после того как она образовалась (через конечный промежуток времени), по

обе стороны ее фронта параметры состояния газа и его скорость (абсолютная

или относительная по отношению к движущемуся фронту) будут иметь зна-

чения, различающиеся между собой на конечные величины. То есть фронт

ударной во

лны представляет собой

поверхность (в данном случае плоскость)

разрыва параметров состояния газа, перемещающуюся по газу и вызываю-

щую скачкообразное изменение этих параметров. В действительности этот

процесс происходит на участке, имеющем длину порядка пути свободного

пробега молекулы; для воздуха она составляет величину ~ 10

-4

см. В данном

случае имеет место внутренний молекулярный процесс, связанный с перехо-

дом кинетической энергии упорядоченного течения газа в кинетическую

энергию беспорядочного теплового движения молекул,  этим объясняется

разогрев газа скачком уплотнения.

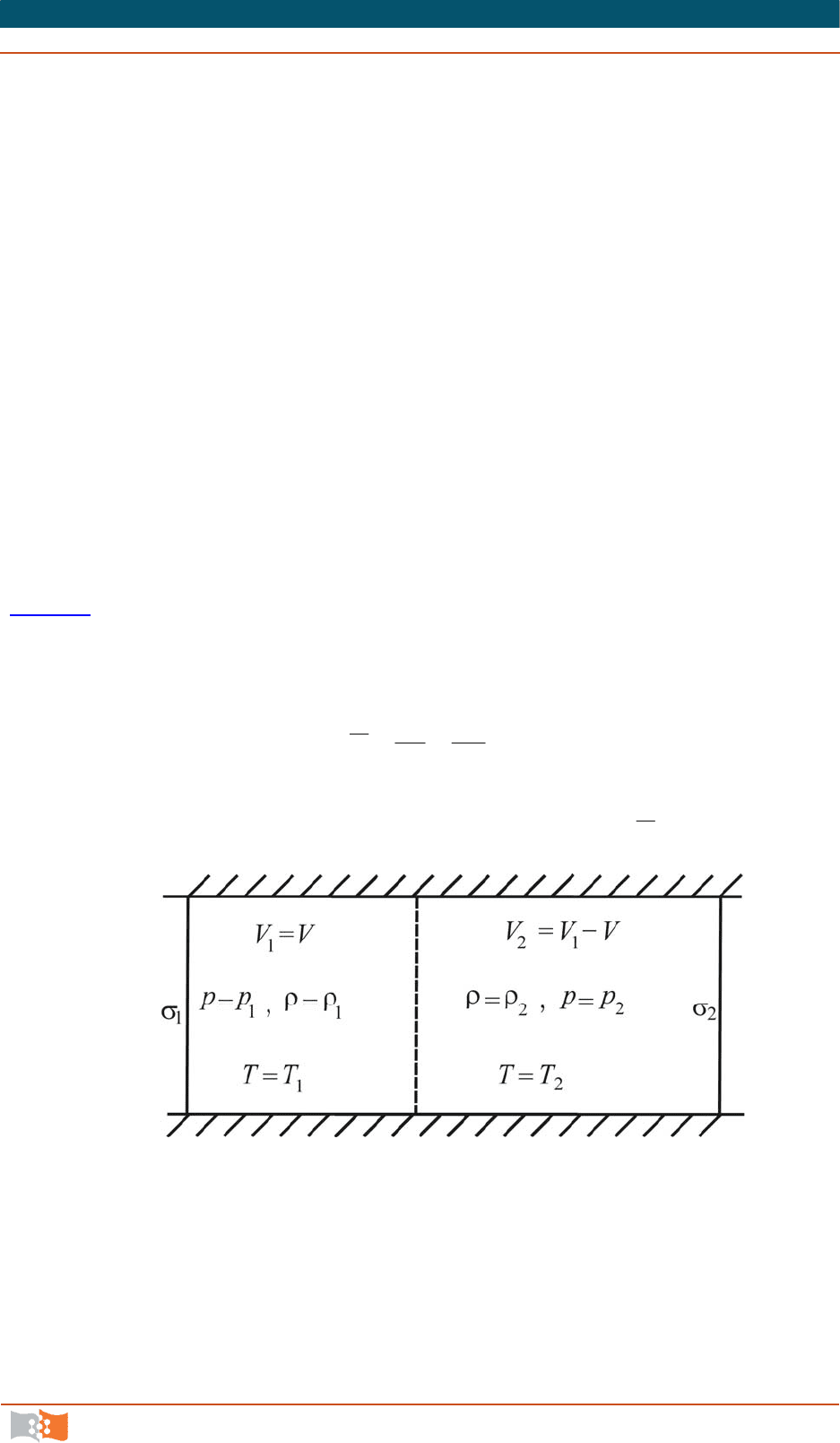
Рассмотрим явление, происходящее в трубе в галилеевой (относитель-

ной) системе координат, связанной с ударной волной (тогда она окажется как

бы остановленной, а движение газа – стационарным). Невозмущенный газ

уже не неподвижен, а подходит к скач

ку уплотнения слева направо

(рис. 7.5

) со скоростью

, а за скачком движется со скоростью

VVV





Уравнения, описывающие это явление, имеют следующий вид

1. Уравнение неразрывности

m 

где

 удельные объемы (здесь масса газа

, протекающая в

одну секунду, отнесена к единице площади).

Рис. 7.5

2. Уравнение количеств движения

222111

VPVP











или

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА

7.2. Теория прямого скачка уплотнения



Гидрогазодинамика. Учеб. пособие 147





1221

PPVVm







3. Уравнение энергии (приток и отвод тепла отсутствуют)

222

111

WPU







где для идеальных газов имеют место формулы для внутренней энер-

гии и энтальпии:

TCPW







;

TCРW

РWUi







Таким образом, составлена система трех уравнений с тремя неизвест-

ными



. Скорости

до и после скачка уплотнения связаны

между собой выведенным Прандтлем соотношением

кр21

aVV 

где

кр

– критическая скорость звука. Из этого соотношения следует,

что если одна из скоростей

или

больше скорости звука, то другая обя-

зательно меньше скорости звука.

Так как все вышеприведенные уравнения совершенно симметричны,

то, казалось бы, возможны как скачки уплотнения, так и скачки разрежения.

Однако если ввести в расчет энтропию в виде































(отсюда следует, что при прохождении газа сквозь воображаемый ска-

чок разрежения



















, а это противоречит второму началу термо-

динамики), то окажется, что физически возможны только скачки уплотнения,

т. к. для замкнутых систем энтропия может только возрастать. Прерывное

разрежение сразу переходит в непрерывную волну разрежения. Таким обра-

зом, скачок уплотнения образуется только в случае

aV 

Если рассмотреть движение ударной волны в покоящемся воздухе, то в

силу обратимости движения сообщим потоку движение V

, направленное

слева направо (рис. 7.4

). Тогда скорость перед скачком уплотнения будет

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА

7.2. Теория прямого скачка уплотнения



Гидрогазодинамика. Учеб. пособие 148

равна нулю, а масса газа позади скачка уплотнения будет двигаться со скоро-

стью V = V

 V

. Уравнение количеств движения в этом случае принимает вид

VVPP

1112







. (7.11)

Таким образом, скорость V

распространения волны уплотнения в по-

коящемся воздухе всегда больше скорости звука и при очень большой разно-

сти давлений может стать чрезвычайно большой, что в действительности и

наблюдается при взрывах.

При расширении газа от давления

до давления

только часть теп-

ловой энергии опять преобразуется в кинетическую. Вследствие потерь энер-

гии (диссипации в тепло) ударная волна, возникшая в неподвижном газе под

влиянием единичного возмущения сжатия, с течением времени затухает.

Если набегающий поток изменяет свое направление, например, при

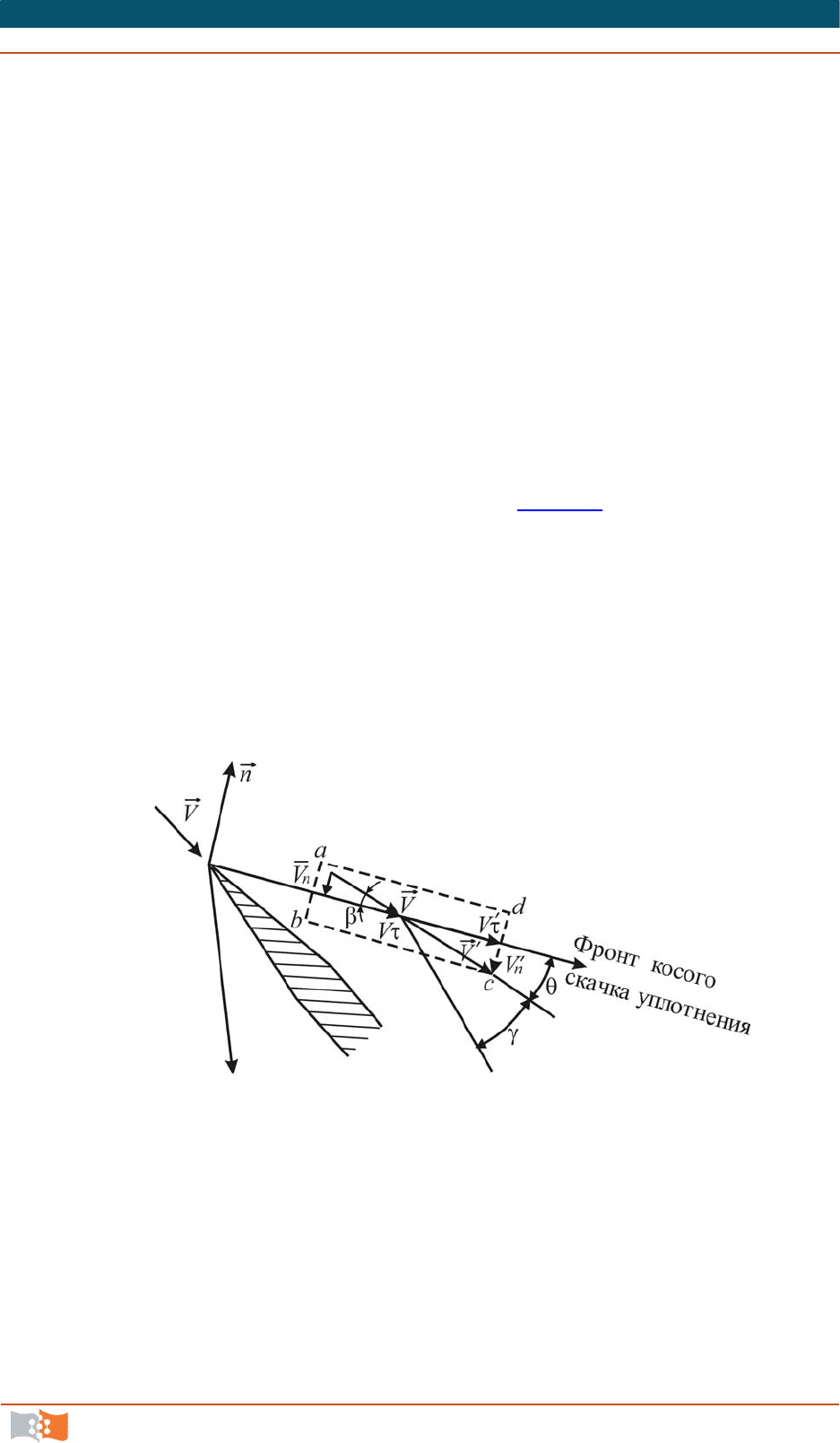
сверхзвуковом обтекании клиновидного тела (рис. 7.6

), то возникает косой

скачок уплотнения. Пусть сверхзвуковой поток газа набегает на косой скачок

уплотнения со скоростью

под углом



к направлению фронта скачка и при

переходе через него отклоняется на угол



, приобретая скорость



Таким образом, после встречи потока с фронтом косого скачка угол



между направлением его фронта и направлением скорости



равен







Разложим векторы скорости



на нормальные и касательные со-

ставляющие









, соответственно параллельные и нормальные

Рис. 7.6

направления фронта косого скачка. Можно показать, что





, а





. Действительно, если в окрестности скачка выделить некоторый объ-

ем

abcd

и применить к нему теорему импульсов, то приложенные к боковым

поверхностям

ab и cd силы взаимно уравновешиваются, т. к.

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА

7.2. Теория прямого скачка уплотнения



Гидрогазодинамика. Учеб. пособие 149







. (7.12)

Применяя формулу (7.11

) для направления, перпендикулярного фронту

скачка, получаем





nnn

VVVPP









. (7.13)

Поскольку давление в скачке уплотнения возрастает (







), то по

условию (7.12

)





. Из (7.12) и (7.13) заключаем, что в косом скачке уп-

лотнения в отличие от прямого претерпевает скачкообразное уменьшение не

полная скорость



потока газа, а только ее нормальная составляющая

Поэтому при одной и той же скорости набегающего потока в слое косого

скачка уплотнения изменение давления, температуры и плотности будет

меньше, чем при прямом скачке уплотнения.

Если все динамические и термодинамические величины потока явля-

ются функциями только одной координаты и времени, то такой поток назы-

вается одномерным.

Рассмотрим задачу о течении газа в трубе, поперечное сечение которой



меняется медленно вдоль оси трубы

. В этом случае можно получить

приближенное решение задачи, используя тот факт, что составляющая скорости

изменяется мало по сечению трубы и поперечные ускорения

малы.

Считая, что жидкость баротропна и массовые силы отсутствуют, мож-

но записать систему уравнений:





















; (7.14)







; (7.15)

МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА

7.3. Обобщенные одномерные движения



Гидрогазодинамика. Учеб. пособие 150







; (7.16)

0div

































; (7.17)











(7.18)

Предположим, что поперечными ускорениями

dtdV /

можно

пренебречь по сравнению с

dtdV /

, приравняв их к нулю. Тогда из (7.15) и

(7.16

) получим приближенные равенства





;





. (7.19)

Отсюда следует, что





txPP ,



, (7.20)

а из (7.18

)





tx ,







Предположим, что

также есть функция только

, т. е. что ос-

тавшимся уравнениям можно удовлетворить, положив





txVV ,

111



Тогда система уравнений (7.14)–(7.18) примет вид













; (7.21)





































; (7.22)











. (7.23)

Данная система уравнений является незамкнутой (здесь пять неизвест-

ных функций). Преобразуем уравнение (7.22

) так, чтобы из него удалить