Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.5. Формы записи уравнений движения в различных системах координат (инерциальных и неинерциальных)
Гидрогазодинамика. Учеб. пособие 111
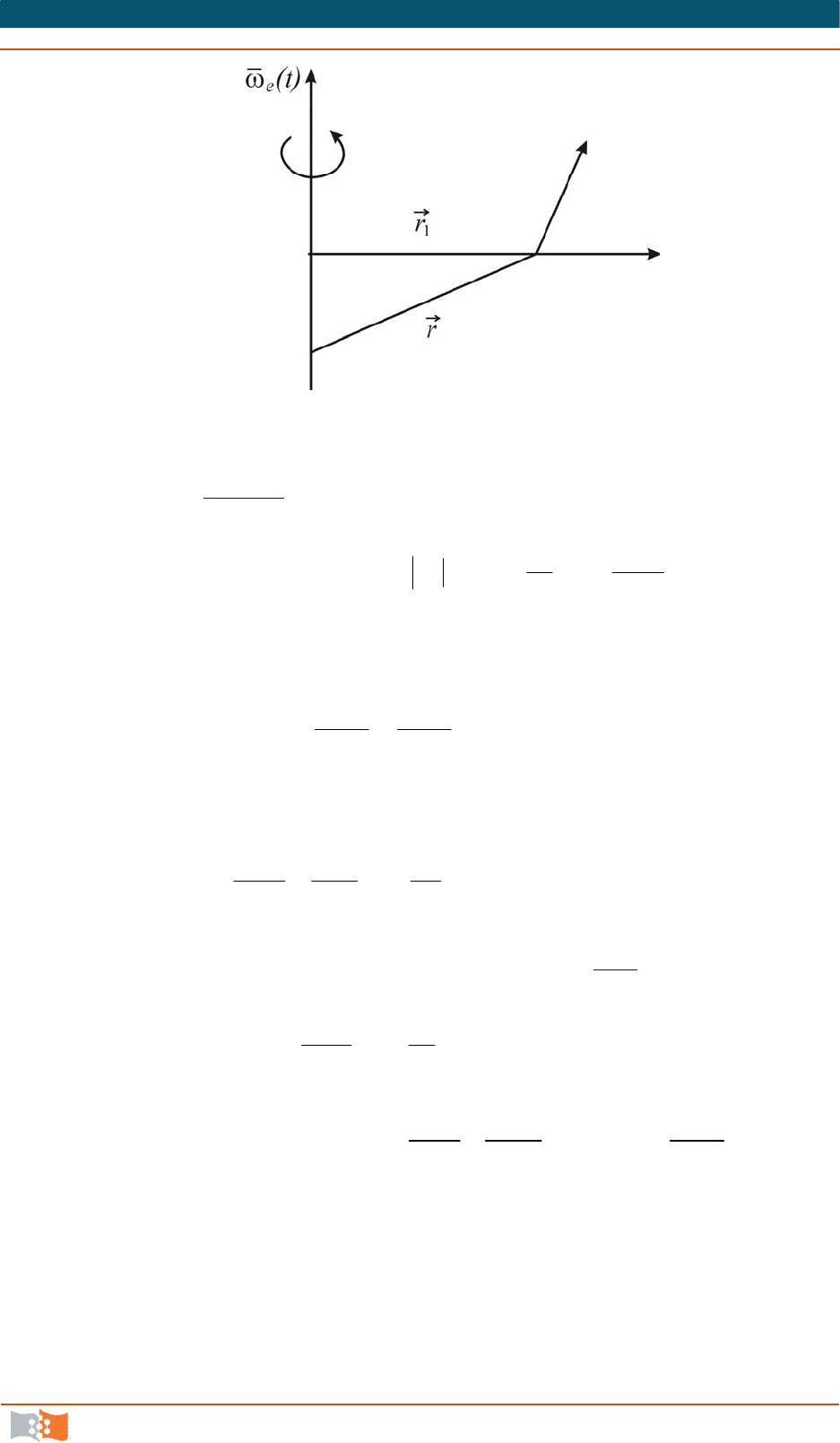
Рис. 5.5
Причем (см. рис. 5.5
)
nее
VQrr
1
,
.
22
2
1
2
2
1
2
1
2
1
2
r
r
rr
e
ееее
По формуле Эйлера имеем для относительной системы координат
rr
rr
r
VV
t
rV
dt
rVd
a
, (5.53)
или, с использованием тождества Громеки Лэмба,
rr
rrrrr
r
VVrot
V
t
V
dt
Vd
a
2
2
. (5.54)
После чего уравнения движения в напряжениях (5.27) примут форму
.
2
Div
2rot
2
2
1
2
0
r
r
dt
d
dt
Vd
F
VV
V
dt
Vd
eeaa
e
rer
rrr
(5.55)
Если инерциальная система движется равномерно (
const
0
V
) и вра-
щается, но с постоянной угловой скоростью (
const
e
), то
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.5. Формы записи уравнений движения в различных системах координат (инерциальных и неинерциальных)
Гидрогазодинамика. Учеб. пособие 112
0
0
dt
Vd
a
,
0
dt
d
ea
,
а кроме того,
ee
V
2rot
и
.VVV
er
rotrotrot
Для такой системы ко-
ординат окончательно будем иметь
,
2
Divrot
2
2
1
2
r
FVV
V
dt
Vd
e
er
rrr
(5.56)
где последний член – объемная плотность центробежных сил с потен-
циалом
2
2
1
2
1
r
U
e
. Для идеальной
P
Div
баротропной
P
жидко-
сти в поле консервативных объемных сил (
UF
e
) будем иметь эти же
уравнения в форме Озеена (для относительного движения):
errr
erer
VVVV
r
U
V
t
V
2rotrot
22
2
1
22
P
(5.57)
при
const
0
V
и
const
e
. Из сопоставления (5.45) и (5.52) можно ус-
тановить, что
,
cererrr
rr
r
r
a
aaaVV
a
dt
Vd
VV
t
V
VV
t
V
VV
t
V
a
r
rr
(5.58)
т. е.
.2
0
reee
eaa
ceer
er
Vrr
dt
d
dt
Vd
aaVV
t
V
(5.59)
Для инерциальной системы координат (
const
0
V
и
0
e
) формула
(5.59
) обращается в тождество вида 0
0, а (5.58) переходит в ранее полу-
ченное соотношение (5.52
).
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
Гидрогазодинамика. Учеб. пособие 113
5
5
.
.
6
6
.
.
П
П
е
е
р
р
в
в
ы
ы
е
е
и
и
н
н
т
т
е
е
г
г
р
р
а
а
л
л
ы
ы
у
у
р
р
а
а
в
в
н
н
е
е
н
н
и
и
й
й
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
Э
Э
й
й
л
л
е
е
р
р
а
а
Для идеальной (
0
ij
;
ji
) баротропной
P
жидкости в поле
консервативных сил
UF
e
можно получить первые интегралы уравне-
ний движения Эйлера, записанные в форме Озеена – в абсолютной, или
инерциальной, системе координат, а также для относительного движения.
Выпишем эти уравнения:
VVU
V
t
V
rot
2
2
P
; (5.60)
VV
r
U
V
t
V
r
e
rot
22
2
1
22
P
. (5.61)
Интеграл Бернулли. Предположим, что течение стационарно, т. е.
0
t
V
. Умножим левую и правую части уравнения (5.60) скалярно на
r
,
причем все перемещения направлены вдоль линии тока, когда
Vr
//
Vr
. Тогда в правой части (5.60) получим тождественный нуль, а в ле-
вой части
0
2
2
PU
V
(5.62)
Следовательно, плотность механической энергии
ÁM
U
V
E const
2
2
P
, или
Á
V
gz const
2
2
P
, (5.63)
остается постоянной вдоль линии тока, а на каждой из линий тока мо-
жет быть свое значение
Б
const
для всех ее точек.
Уравнение Бернулли, полученное как первый интеграл уравнений Эй-
лера, означает не что иное, как утверждение о сохранении механической
энергии. В соответствии с этим первые два слагаемых в (5.63
) представляют
собой соответственно потенциальную энергию положения и объемного дей-
ствия поверхностных сил, а третье – удельную кинетическую энергию
(см. вторую форму записи).
При записи уравнения Бернулли в виде

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.6. Первые интегралы уравнений движения Эйлера
Гидрогазодинамика. Учеб. пособие 114
Á
V
gz const
2
2
P
слагаемые трехчлена называют соответственно геометрическим, пье-
зометрическим и скоростным напором.
Уравнение Бернулли можно использовать для расчетов гидромашин
(рабочих колес гидротурбин, насосов и т. д.) в случае относительного движе-
ния жидкости в равномерно вращающейся вокруг неподвижной оси системе
координат. В относительной системе координат, например связанной с вра-
щающимся рабочим колесом, поток жидкости стационарен, и применение
теоремы Бернулли возможно (в отличие от абсолютного по
тока).
Если аналогичную процедуру выполнить для уравнений (5.61
), т. е. ин-
тегрируя вдоль линий тока относительного движения, то
r
Á
e
r
r
M
r
U
V
E const
22
2
1
2
2
P
. (5.64)
При стационарном течении в относительной системе координат
0
t
V
r
в силу (5.64
) уравнения (5.61) дают
0rot VV
r
условие Н. Е.
Жуковского
(Ф. И. Франкль и М. В. Келдыш в 1935 г. показали, что это условие является
первым, но достаточно сильным приближением). Это означает, что вихри аб-
солютного движения располагаются вдоль линий тока относительного движе-
ния:
V//V
r
rot
. (5.65)
При малых нагрузках
e
VV
, т. е.
eer
VVVV
,
условие Н. Е. Жуковского переходит в линеаризированное условие
.0rotrot
2
er
VVVV
(5.66)
Это означает, что вихри абсолютного движения при малых нагрузках
располагаются примерно вдоль линии тока переносного течения, которое
всегда известно.
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.6. Первые интегралы уравнений движения Эйлера
Гидрогазодинамика. Учеб. пособие 115
Интеграл Громеки. При стационарном течении
0
t
V
можно интег-
рирование (5.60
) провести и вдоль вихревых линий, принимая
V//rδ
rot
. То-
гда
ГM
U
V
E const
2
2
P
(5.67)
будет вдоль вихревых линий, где
Г
const
одна и та же для всех гео-
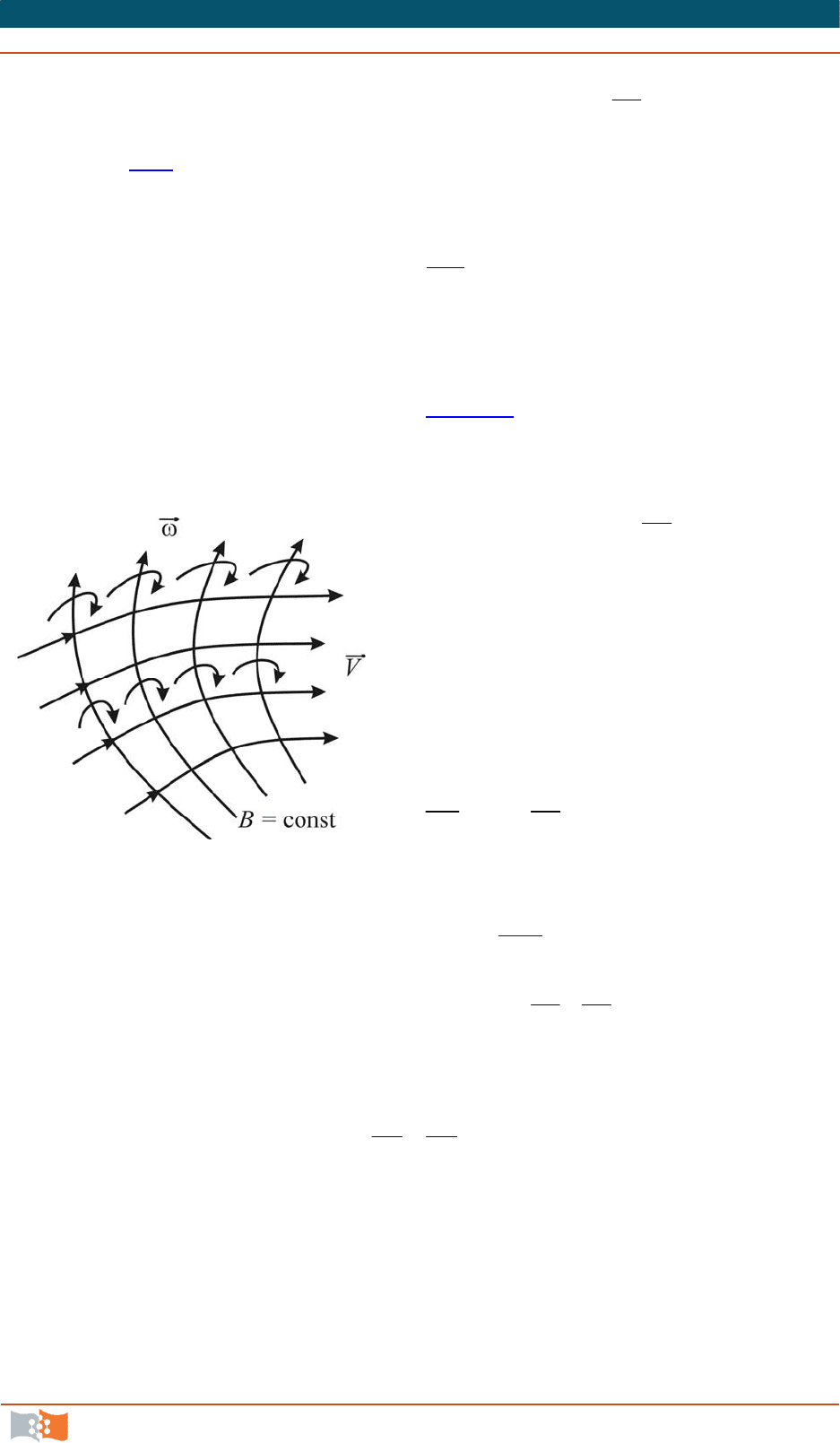
метрических точек на одной и той же вихревой линии. Если линии тока и вих-
ревые линии образуют поверхности (рис. 5.6
), то для них очевидно, что
ΓБ
constсonst
;
const
2
2
PU
V
E
M
(5.68)
или эти поверхности являются
энергетическими поверхностями.
Интеграл Коши Лагранжа.
Пусть
0rot V
, т. е.
gradV
(в силу
теоремы Стокса). Учтем также, что
t
t
V
grad
(дифференцирование по
независимым переменным
t
и
i
x
можно
поменять местами для непрерывной
).
Тогда (5.60
) принимает вид
0
2
2
U
V
dt
d
P
, (5.69)
т. е.
ËÊM
U
V
d
t
d
t
E
const
2
2
P
. (5.70)
Причем
ЛК
const
одна и та же для всех геометрических точек всего
пространства Е
3
или той его части, которая заполнена жидкостью или газом.
Рис. 5.6

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.6. Первые интегралы уравнений движения Эйлера
Гидрогазодинамика. Учеб. пособие 116
Интеграл Эйлера. Имеем
0rot V
;
gradV
, и течение стационарно
–
0
dt
d
. В этом случае
ÝM
U
V
E const
2
2
0
P
. (5.71)
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
Гидрогазодинамика. Учеб. пособие 117
5
5
.
.
7
7
.
.
П
П
р
р
и
и
м
м
е
е
н
н
е
е
н
н
и
и
е
е
у
у
р
р
а
а
в
в
н
н
е
е
н
н
и
и
я
я
Б
Б
е
е
р
р
н
н
у
у
л
л
л
л
и
и
Рассмотрим случаи, когда интеграл Бернулли позволяет очень просто
решать задачи о движении жидкости.
Пример.
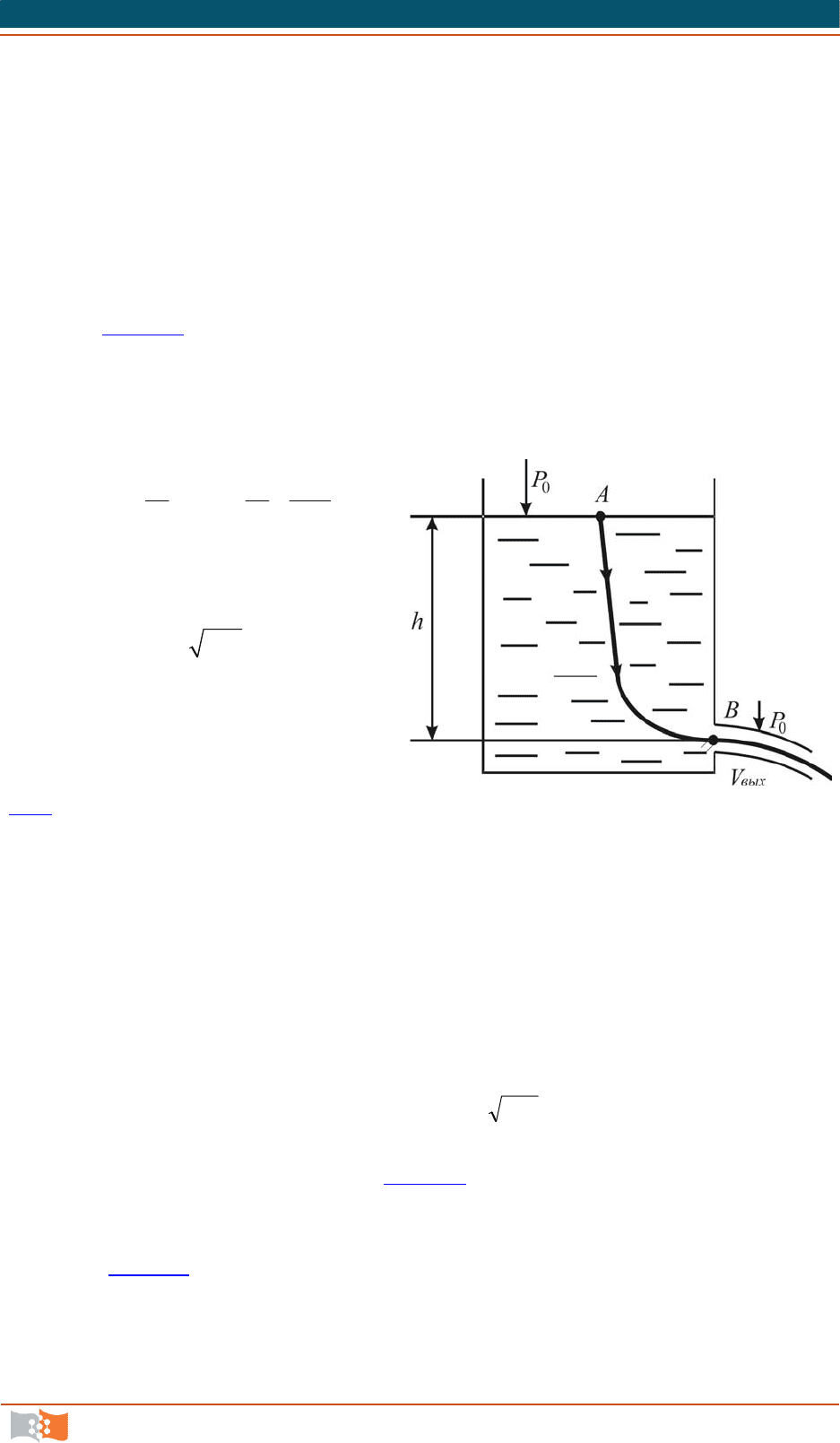
Истечение жидкости из резервуара при постоянном напоре.
Предположим, что размеры резервуара, из отверстия которого вытекает вода
со скоростью V
вых
, настолько велики, что падением уровня в нем можно пре-
небречь (рис. 5.7
). Давление на поверхность воды в резервуаре и на боковую
поверхность струи равно
0
P
(или в данном случае атмосферному). Напишем
уравнение Бернулли для некоторой линии тока
A
B
. Скорость на свободной
поверхности резервуара примем равной нулю, тогда
2
00
2
вых
AB
PPV
gz gz
,
отсюда
2
вых
Vgh
. (5.72)
Скорость
вых
V
равна скоро-
сти предмета, свободно падаю-
щего с высоты
h . Равенство
(5.72
) выражает собой т. н. теоре-
му Торичелли.
Поперечное сечение струи,
вытекающей из сосуда, не равно поперечному сечению отверстия. Скорости
частиц жидкости в момент выхода из отверстия не параллельны друг другу и
имеют компоненту, направленную к центру струи: струя сужается. Отноше-
ние площади поперечного сечения струи к площади отверстия называют ко-
эффициентом сжатия
. Объемный расход в этом случае вычисляют по фор-
муле
ghSQ 2
. (5.73)
Пример.
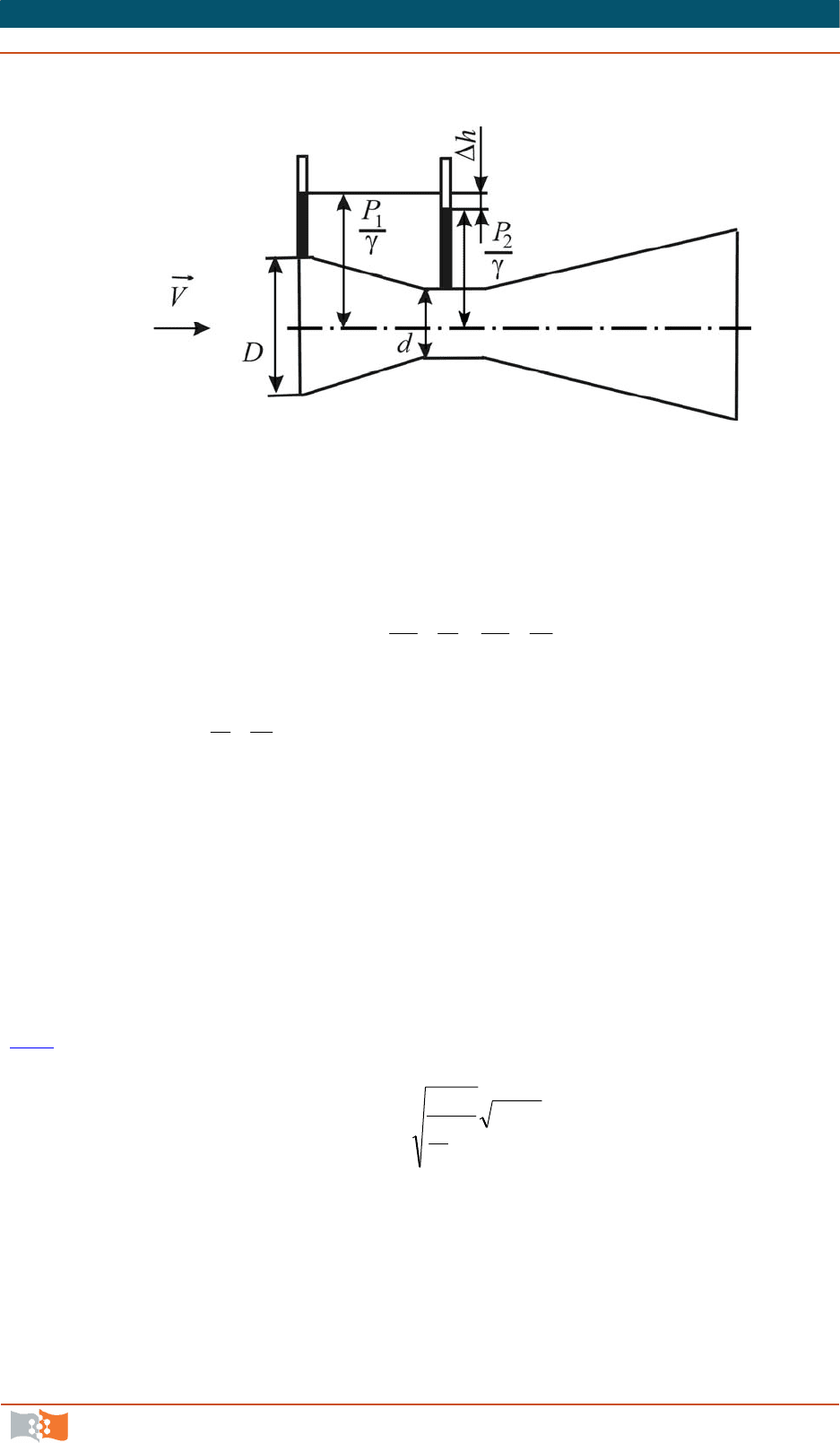
Водомер Вентури (рис. 5.8) используется для измерения рас-
ходов жидкости и представляет собой трубу с пережатием определенных
размеров и формы. По оси прибора устанавливаются два пьезометра, как по-
казано на рис. 5.8
.
Рис. 5.7
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.7. Применение уравнения Бернулли
Гидрогазодинамика. Учеб. пособие 118
Рис. 5.8
Если применим теорему Бернулли к линии тока, расположенной, на-
пример, на оси водомера, имеем:
2
2
21
2
1
22
P
g
VP
g
V
. (5.74)
Обозначим
21
PP
через h
, где h
разность пьезометрических
высот, считываемая по шкале прибора и отражающая уменьшение давления в
потоке жидкости в сжатом сечении вследствие увеличения скорости потока.
Зная, что
2211
SVSVQ
,
где
,
1
S
2
S
– площади сечений в плоскости соответственно 1-го и 2-го
пьезометров, и выражая скорости через размеры водомера при подстановке в
(5.74
), получим в окончательном виде
hg
d
D
SQ
2
1
1
1
.
В данном случае не учитывали потери энергии при прохождении жид-
кости через водомер, неравномерность распределения скоростей в контроль-
ных сечениях.

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
Гидрогазодинамика. Учеб. пособие 119
5
5
.
.
8
8
.
.
Ц
Ц
и
и
р
р
к
к
у
у
л
л
я
я
ц
ц
и
и
о
о
н
н
н
н
о
о
е
е
о
о
б
б
т
т
е
е
к
к
а
а
н
н
и
и
е
е
к
к
р
р
у
у
г
г
л
л
о
о
г
г
о
о
ц
ц
и
и
л
л
и
и
н
н
д
д
р
р
а
а
п
п
о
о
т
т
е
е
н
н
ц
ц
и
и
а
а
л
л
ь
ь
н
н
ы
ы
м
м
п
п
о
о
т
т
о
о
к
к
о
о
м
м
Известно, что если у нас есть безвихревая несжимаемая жидкость, то
поток удовлетворяет следующим двум уравнениям:
,0 V
0 V
. (5.75)
Хотя при всех потенциальных (безвихревых) течениях циркуляция в
любой малой области потока равна нулю, тем не менее существуют такие по-
тенциальные течения, в которых циркуляция для всего потока не равна нулю.
Необходимым условием для этого является многосвязность области, в кото-
рой происходит течение.
В рамках топологии – геометрии, не связанной с метрич
ескими соот-
ношениями, а рассматривающей взаимное расп
оложение геометрических тел,
выясняется необходимость классификации пространств по их «связности».
Пространство называется односвязным, если любой замкнутый контур в нем
может быть непрерывно стянут в точку, и многосвязным (одно-, двух- и т. д.),
если этого сделать нельзя, не выходя за пределы рассматриваемой области. При-
мером двухсвязной области мо
жет служи
ть комната с колонной посередине.
Отметим одну важную особенность, которая наблюдается в случае не-
сжимаемого потенциального потока (в общем случае ее нет): если имеется
какое-то первое решение и какое-то второе, то сумма их также будет реше-
нием. Это справедливо в силу линейности уравнений (5.75
). Полный же на-
бор гидродинамических уравнений
PFVV
V
t
V
grad
1
rot
2
grad
2
, (5.76)
0
V
t
, (5.77)
V
(5.78)
нелинеен если взять ротор (rot) от обеих частей уравнения (5.76
) при
сonst
с использованием уравнения (5.75), получим уравнение (5.77).
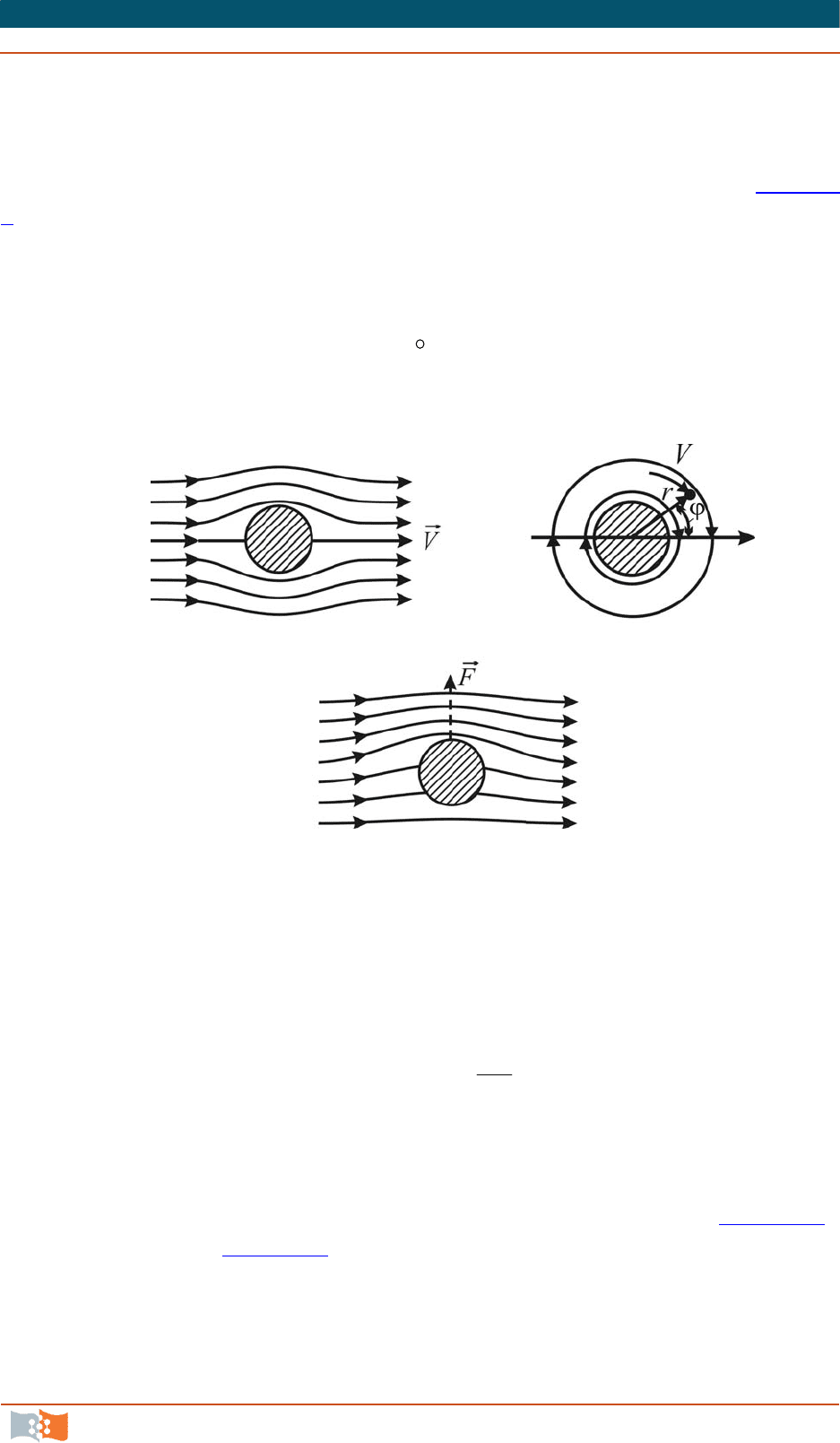
Однако в случае безвихревого потока вокруг цилиндра можно полу-
чить циркуляционное обтекание, наложив на простейший плоскопараллель-
ный поток (рис. 5.9, a
), определяемый потенциалом скоростей
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.8. Циркуляционное обтекание круглого цилиндра потенциальным потоком
Гидрогазодинамика. Учеб. пособие 120
ñ
, (5.79)
где c коэффициент Лапласа, круговой (циркуляционный) (рис 5.9,
б).
Для кругового пути с центром, совпадающим с центром цилиндра,
криволинейный интеграл от скорости равен
S
rVdSV 2
. (5.80)
а б
в
Рис. 5.9
Для потенциального течения интеграл не должен зависеть от
r
. Тогда
r
V
2
, (5.81)
где
V
тангенциальная скорость.
В результате такого наложения получим новый вид потока (рис. 5.9, в
).
Даже без расчета из рис. 5.9, в
, следует, что в слоях жидкости над цилиндром
скорости бесциркуляционного обтекания цилиндра и чисто циркуляционного
потока вокруг цилиндра складываются, а под цилиндром вычитаются. При
этом скорость на верхней стороне цилиндра оказывается больше, а давле-
