Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.2. Закон сохранения массы. Уравнение неразрывности
Гидрогазодинамика. Учеб. пособие 101
В случае стационарного поля плотности (локальная производная
0
t
)
.0div V
(5.14)
В частном случае несжимаемой жидкости (
cons
t
) уравнение (5.14)
называется
уравнением несжимаемости:
.0div
3
3
2
2
2
1
x
V
x
V
x
V
V
(5.15)
Для несжимаемых жидкостей
0
1
div
dt
d
d
V
, (5.16)
т. е.
0
V
tdt
d
. (5.17)
Расписав (5.12) в проекциях, получим выражение для практических
вычислений:
.0
3
3
2
2
1
1
3
3
2
2
1
1
x
V
x
V
x
V
x
V
x
V
x
V
t
(5.18)
Учитывая, что
dt
d
V
t
, можно (5.12) придать более компактную
форму:
0 div
V
dt
d
.
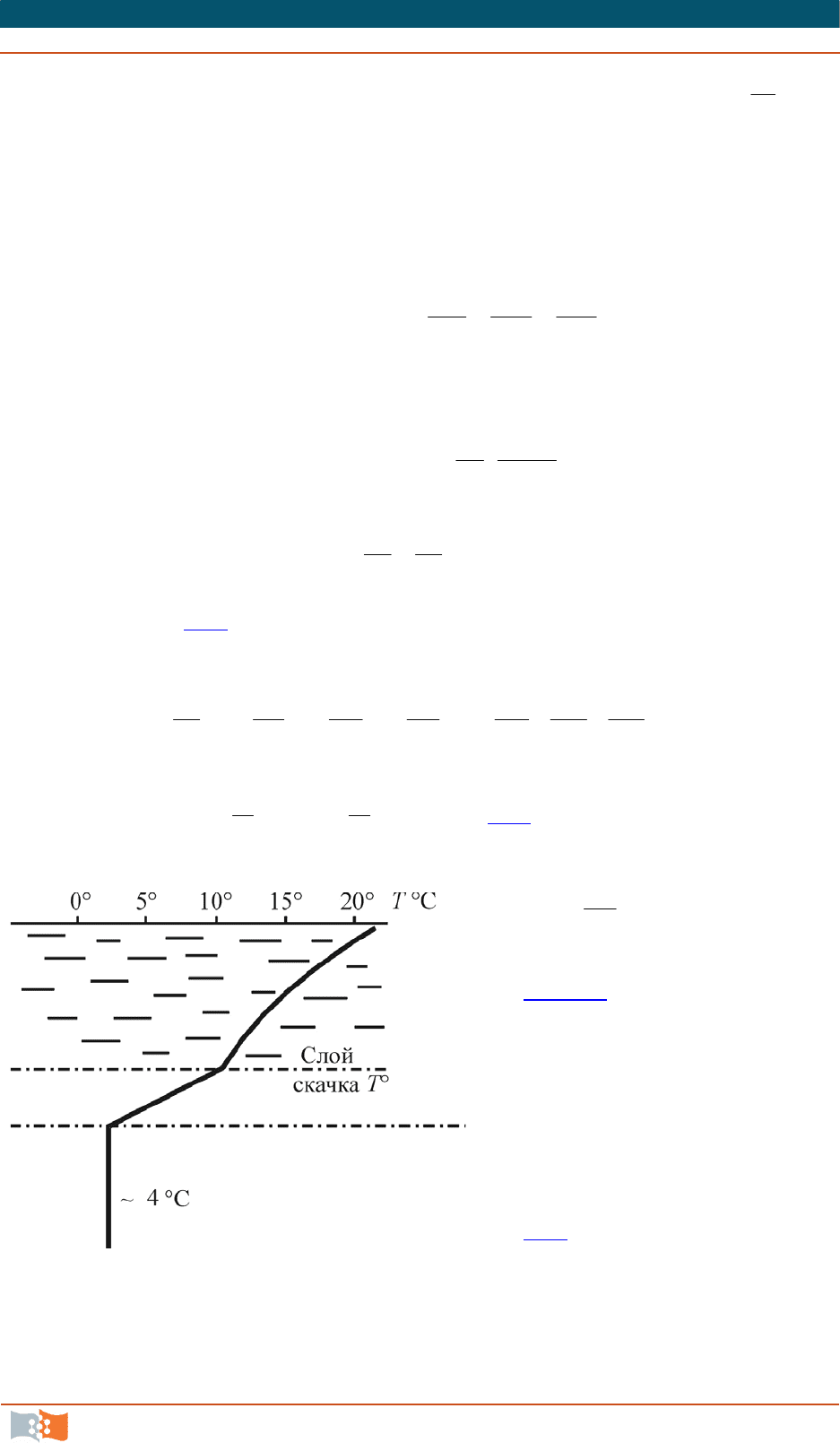
Для морской воды
(рис. 5.2
) или воды в прудах-
охладителях ТЭС и АЗС с из-
менением температуры
,
i
Txt
плотность
также будет
функцией
,
i
x
t
, но ее рас-
пределение в пространстве
должно подчиняться закону
(5.17
). Для сжимаемых жид-
костей (например, газа, воз-
духа)
0div V
и должен все-
гда соблюдаться закон
Рис. 5.2
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.2. Закон сохранения массы. Уравнение неразрывности
Гидрогазодинамика. Учеб. пособие 102
(5.18a). Если же плотность – физическая константа (в большинстве случаев для
капельных жидкостей, в т. ч. и для воды):
0
const
,
то
0
0
0
V
dt
d
.
Тогда уравнение неразрывности вырождается в более простое:
0div V
,
каковым и следует пользоваться для несжимаемых жидкостей (как ка-
пельных, так и газообразных при малых давлениях и числах Маха
1
0
0
C
V
M
).
Исходя из условия неразрывности движущейся материальной среды
следует считать, что, если среда несжимаема, дивергенция вектора скорости
должна быть равна нулю в любой точке пространства, занятого потоком. Это
положение можно рассматривать и в ином (обратном) смысле, т. е. равенство
нулю дивергенции вектора скорости считать признаком несжимаемой дви-
жущейся сплошной материальной среды. Этим определяется и принципиаль-
ная возможность оценивать дивергенцией вектора скорости объемные де-
формации в движущей
ся сп
лошной материальной среде, что используется
при определении нормальных напряжений.
Рассмотрим, как записываются в конкретных случаях уравнения нераз-
рывности.
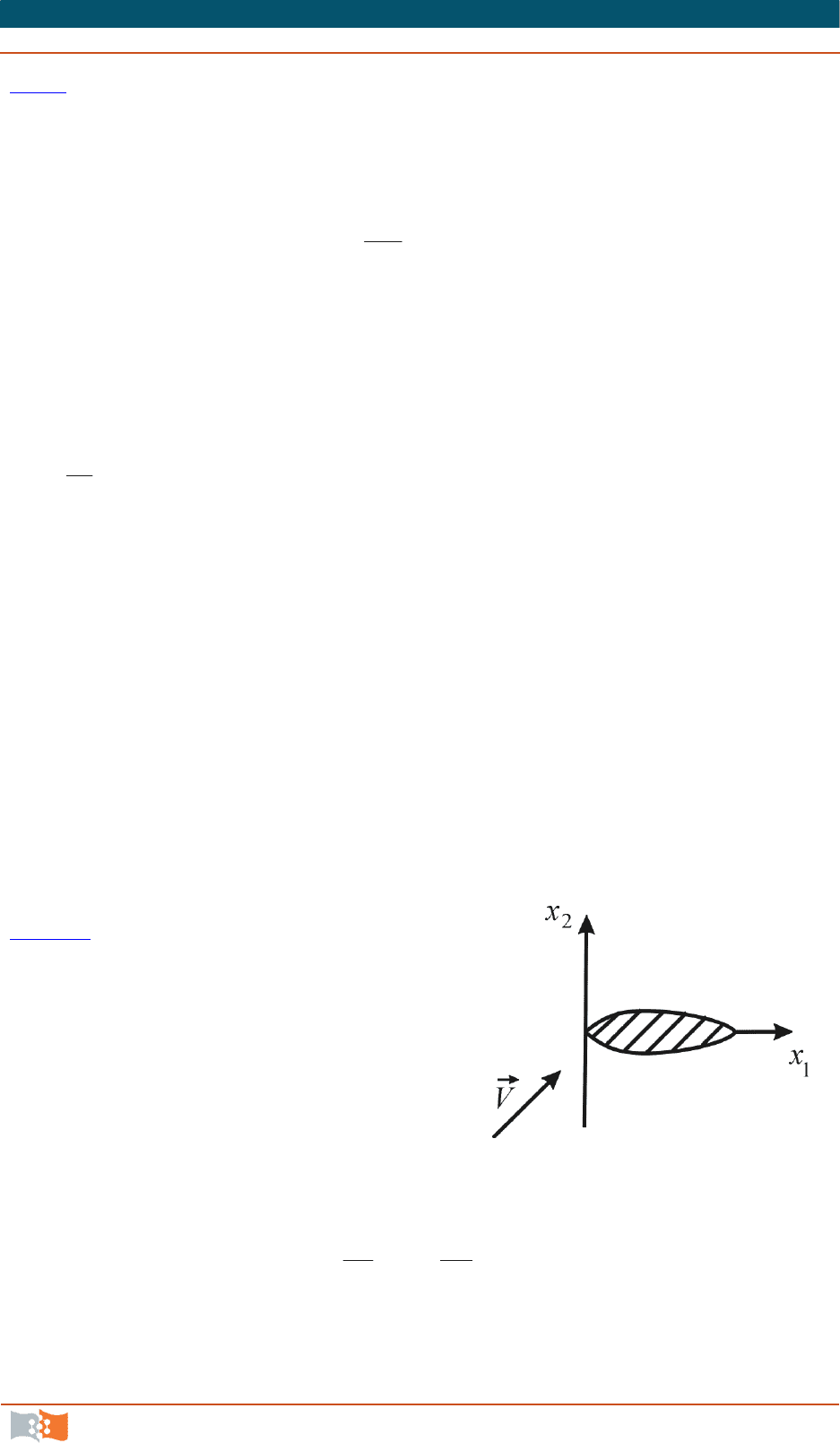
Пример. Какой вид имеют уравнения неразрывности в декартовых ко-
ординатах, используемые для исследования установившегося обтекания
сжимаемой жидкостью профиля крыла
(рис. 5.3
).
Для установившихся течений па-
раметры жидкости являются функция-
ми только координат точек, следова-
тельно, частные производные парамет-
ров по времени обращаются в нуль. А
для плоских установившихся течений
сжимаемой жидкости около профиля
крыла уравнение неразрывности запи-
сывается в виде
0
2
2
1
1
V
x
V
x
.
Рис. 5.3

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
Гидрогазодинамика. Учеб. пособие 103
5
5
.
.
3
3
.
.
У
У
р
р
а
а
в
в
н
н
е
е
н
н
и
и
я
я
Э
Э
й
й
л
л
е
е
р
р
а
а
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
н
н
е
е
в
в
я
я
з
з
к
к
о
о
й
й
ж
ж
и
и
д
д
к
к
о
о
с
с
т
т
и
и
Движение жидкости подчиняется законам Ньютона и на их основе опи-
сывается системой, состоящей из уравнений количества и момента количест-
ва движения.
Предположим, что на движущуюся жидкость действуют объемные си-
лы
F
. Общие уравнения движения невязкой жидкости могут быть получены
из дифференциальных уравнений равновесия (3.6
), если, согласно принципу
Д’ Аламбера, к действующим силам добавить силы инерции. Тогда уравне-
ние движения запишем так:
PFVV
t
V
dt
Vd
grad
1
. (5.19)
Здесь
J
dt
Vd
– силы инерции, отнесенные к единице массы и объема.
В проекции на оси декартовых прямоугольных координат уравнение Эйлера
примет вид
.
1
,
1
,
1
3
3
3
3
3
2
3
2
1
3
1
3
2
2
3
2
3
2
2
2
1
2
1
2
1
1
3
1
3
2
1
2
1
1
1
1
x
P
F
x
V
V
x
V
V
x
V
V
t
V
x
P
F
x
V
V
x
V
V
x
V
V
t
V
x
P
F
x
V
V
x
V
V
x
V
V
t
V
(5.20)
Сделав предположение об идеальности жидкости (невязкости, т. е. об
отсутствии в жидкости касательных напряжений трения) и добавив к (5.20
)
уравнение несжимаемости (5.18
), получим замкнутую систему уравнений
динамики Эйлера.
Для решения определенной задачи необходимо задаться начальными и
граничными условиями. Начальными условиями будут:
, , ,
321101
xxxVV
, , ,
321202
xxxVV
, , ,
321303
xxxVV
3210
, , xxxPP
при t = t
0
. Если движе-
ние стационарное (установившееся), начальные условия опускаются.
Граничные условия:
1) условие непроницаемости твердых границ потока, т. е. нормальная
составляющая скорости к поверхности канала (трубы, русла и т. п.) во всех
его точках должна быть равна нулю; касательная составляющая произвольна.
В случае вязкой жидкости это условие заменяется условием «прилипаемо-
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.3. Уравнения Эйлера движения невязкой жидкости
Гидрогазодинамика. Учеб. пособие 104
сти» жидкости к стенкам канала, т. е. условием равенства скоростей жидко-
сти и точек твердой поверхности, по которой она движется.
Условие непроницаемости является общим для задач как внешнего об-
текания тел (обтекание лопасти турбины или рабочего колеса насоса, любого
тела, движущегося в жидкости и т. п.), так и внутреннего (задач, связанных с
течением жидко
с
ти в проточной части гидромашин, в трубках, реках и т. д.);
2) задание поля скоростей вдалеке (на бесконечности) от обтекаемого
тела (в случае внешнего обтекания) и секундного объемного расхода жидко-
сти сквозь любое сечение канала (внутреннее обтекание).
В рассмотренной общей постановке задач динамики невязкой жидко-
сти решение этих уравнений представля
ет сущест
венные трудности. Во-
первых, уравнения динамики Эйлера записываются в частных производных,
т. е. это не обыкновенные дифференциальные уравнения, и, во-вторых, эти
уравнения нелинейны из-за наличия в них конвективных членов. Решение
этих уравнений в большинстве случаев возможно лишь с помощью числен-
ных методов.
5
5
.
.
4
4
.
.
З
З
а
а
к
к
о
о
н
н
и
и
м
м
п
п
у
у
л
л
ь
ь
с
с
о
о
в
в
.
.
У
У
р
р
а
а
в
в
н
н
е
е
н
н
и
и
я
я
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
в
в
н
н
а
а
п
п
р
р
я
я
ж
ж
е
е
н
н
и
и
я
я
х
х
Математическая формулировка закона импульсов была дана И. Ньюто-
ном в трактате «Nature Fhylosofical» (1654 г.) Анализируя кинематические
законы Кеплера о движении планет, И. Ньютон обратил внимание, что для
всех этих законов оказывается справедливым условие
F
r
r
r
M
k
dt
rd
m
dt
Vd
mam
22
2
. (5.21)
Тем самым он открыл закон всемирного тяготения, физическая приро-
да которого до сих пор не ясна. Одновременно он обобщил законы кинема-
тики и сформулировал ставший знаменитым второй закон механики:
Fam
.
Применительно к жидкости закон импульсов записывается в форме
SFV
dt
d
S
ne
, (5.22)
где
n
n
,
тензор напряжений в среде. Используя преобразо-
вание Остроградского
Гаусса, получим
S
Sn Div
.
5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.4. Закон импульсов. Уравнения движения в напряжениях
Гидрогазодинамика. Учеб. пособие 105
Применив формулу Эйлера (5.7), получим
.
div
VV
dt
Vd
VV
t
VV
dt
d
(5.23)
По уравнению неразрывности (5.12) первый интеграл тождественно
равен нулю. Тогда
Div
e
FVV
dt
Vd
. (5.24)
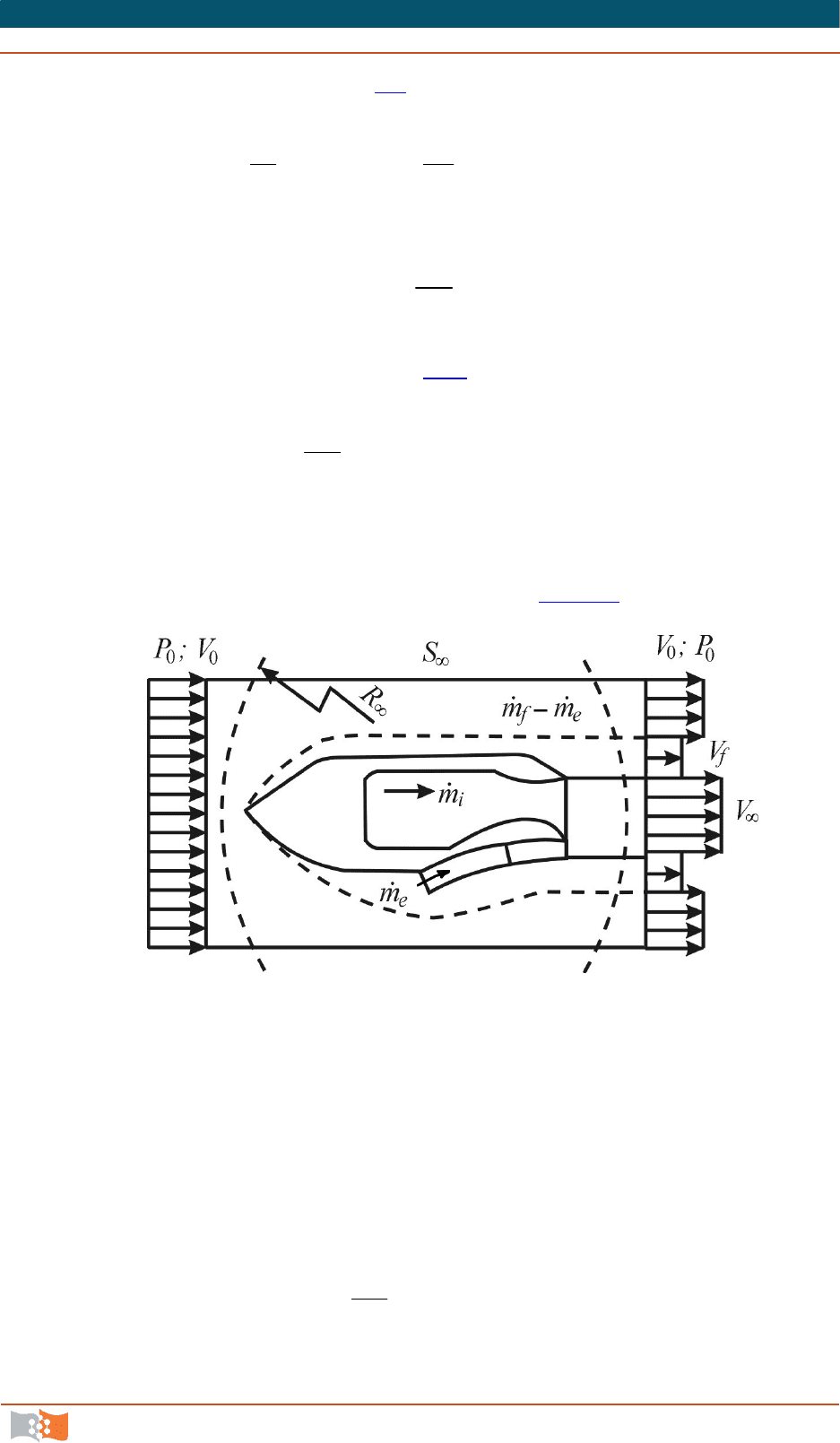
Эта интегральная форма закона импульсов МЖГ удобна при вычисле-
нии суммарных нагрузок (и главного вектора внешних сил, действующих со
стороны жидкости на движущееся в ней тело, см. рис. 5.4
).
Рис. 5.4
fefei
VVmmVVmVmz
00
.
Если
,
0 fff
VVmR
то
feife
VVmVmRzP
.
Стягивая объем τ в точку (или опираясь на произвольность его выбо-
ра), получим дифференциальную форму закона импульсов для МЖГ:
Div
e
FVV
t
V
. (5.25)

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.4. Закон импульсов. Уравнения движения в напряжениях
Гидрогазодинамика. Учеб. пособие 106
Его называют в МЖГ уравнением движения в напряжениях. Используя
тождественное преобразование Громеки
Лэмба:
VV
V
VV
rot
2
2
, (5.26)
(5.25
) можно придать форму
Divrot
2
2
e
FVV
V
t
V
. (5.27)
Для ньютоновских жидкостей, т. е. когда имеется линейная зависи-
мость между тензором напряжений
и тензором скоростей деформаций
S
(обобщенный закон Ньютона), получаем
SIVP
2div
3
2
и
VSVVvP
div
3
1
grad 2 di grad
3
1
Div
. (5.28)
Уравнение движения в напряжениях принимает вид
.div
3
1
grad2
div grad
3
1
grad
ЛЛэмб Громеки форма
rot
2
Эйлера форма
2
VSV
VP
VV
V
dt
Vd
VV
dt
Vd
(5.29)
Лэмба

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.4. Закон импульсов. Уравнения движения в напряжениях
Гидрогазодинамика. Учеб. пособие 107
Обычно пренебрегают изменением
T,
от давления и температуры,
т. е. полагают
0gradgradgrad
T
dT
d
P
d
d
.
В случае несжимаемых жидкостей
0div V
уравнения движения
VPFVV
t
V
e
2
grad
(5.30)
были феноменологически получены Навье и теоретически обоснованы
Стоксом. Поэтому (5.30
) называют уравнениями Навье
Стокса. Для иде-
альной несжимаемой жидкости (когда касательными напряжениями и вязко-
стью можно пренебречь,
0
) будем иметь уравнения, известные еще Эй-
леру:
PFVV
t
V
e
grad
. (5.31)
В случае баротропной жидкости
P
в поле консервативных сил
UF
e
grad
можно ввести функции
P
dP
tx
i
,P
и
1
P
. (5.32)
Тогда уравнение движения Эйлера (5.31
) можно записать в форме
Озеена:
,P
UVV
V
t
V
VV
t
V
rot
2
2
(5.33)
или
VVU
V
t
V
rot
2
2
P
. (5.34)

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.4. Закон импульсов. Уравнения движения в напряжениях
Гидрогазодинамика. Учеб. пособие 108
Последняя форма более удобна для интегрирования. Векторному урав-
нению (5.25
) всегда соответствуют три скалярных (в проекции на оси коор-
динат). Так, для декартовой системы координат будем иметь, например,
k
ki
e
k
i
k
i
dx
d
F
x
V
V
t
V
i
, (5.35)
где индексы
i
и
k
проходят значения от 1 до 3, причем по дважды
встречающемуся индексу
k
производится суммирование, т. е.
3
1
3
2
1
2
3
1
1
1
1
11
dx
dV
V
dx
dV
V
dx
dV
V
dx
dV
V
dx
dV
V
k
k
k
k
k
(5.36)
и аналогично
3
1
3
31
2
21
1
11
k
k
ki
k
ki
dx
d
dx
d
dx
d
dx
d
dx
d
. (5.37)
5
5
.
.
5
5
.
.
Ф
Ф
о
о
р
р
м
м
ы
ы
з
з
а
а
п
п
и
и
с
с
и
и
у
у
р
р
а
а
в
в
н
н
е
е
н
н
и
и
й
й
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
в
в
р
р
а
а
з
з
л
л
и
и
ч
ч
н
н
ы
ы
х
х
с
с
и
и
с
с
т
т
е
е
м
м
а
а
х
х
к
к
о
о
о
о
р
р
д
д
и
и
н
н
а
а
т
т
(
(
и
и
н
н
е
е
р
р
ц
ц
и
и
а
а
л
л
ь
ь
н
н
ы
ы
х
х
и
и
н
н
е
е
и
и
н
н
е
е
р
р
ц
ц
и
и
а
а
л
л
ь
ь
н
н
ы
ы
х
х
)
)
Предыдущие законы и уравнения записывали в абсолютно неподвиж-
ной системе для любой инерциальной системы координат (согласно третьему
постулату Галилея Ньютона). Покажем это конкретно. Пусть система коор-
динат инерциальна, т. е. движется равномерно и поступательно с постоянной
скоростью
0
const VV
e
. Тогда
rãe
VVVVV
0
, (5.38)
где
txV
ir
,
относительная скорость.
Так как для такой инерциальной системы координат
0
0
dt
Vd
и
0
0
i
dx
Vd
,
то
0
00
0
00
i
i
dx
Vd
V
dt
Vd
VV
t
V
dt
Vd
; (5.39)

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.5. Формы записи уравнений движения в различных системах координат (инерциальных и неинерциальных)
Гидрогазодинамика. Учеб. пособие 109
.
0
00
0
rr
rr
rrr
ra
rr
raaa
VV
t
V
VV
dt
Vd
VV
t
V
VVVVV
t
VV
VV
t
V
dt
Vd
r
(5.40)
Следовательно, уравнения движения в напряжениях не изменяют свой
вид:
,Div
e
FVV
dt
Vd
dt
Vd
(5.41)
Div
err
rr
FVV
t
V
. (5.42)
Итак, индекс r переносного движения для инерциальной системы коор-
динат можно опускать. Однако для неинерциальных систем координат (дви-
жущейся неравномерно или с вращением) этого сделать нельзя. Покажем это.
Пусть переносная скорость
ieie
xrttVtxV ,
0
. (5.43)
Тогда абсолютная скорость
txV
i
,
представима так:
txV
i
,
=
txVtxV
iriе
,,
(5.44)
или
txV
ir
,
=
txVtxV
iei
,,
, (5.45)
.
VVVV
t
V
VV
t
V
VV
t
V
dt
Vd
e
r
e
ra
(5.46)
Можно установить, что

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
5.5. Формы записи уравнений движения в различных системах координат (инерциальных и неинерциальных)
Гидрогазодинамика. Учеб. пособие 110
VV
t
V
t
V
e
ra
, (5.47)
и уравнения абсолютного движения в напряжениях, но для неинерци-
альной системы координат, примут вид
.Div
er
ra
FVV
t
V
VV
t
V
(5.48)
Уравнениям (5.47
,5.48) можно придать и другую форму:
.Div
er
ra
FVVVV
t
V
VV
t
V
(5.49)
Уравнение (5.49
) часто используют для описания абсолютного движе-
ния в относительной системе координат.
Покажем также запись относительного движения в относительной (не-
инерциальной) системе координат, что очень удобно при описании движения
жидкости во вращающихся механизмах (планетарных задачах в масштабах
вращающейся Земли и др.). Напомним основные положения теоретической
механики об абсолютном, переносном и относительном движениях:
rrr
a
0
;
e
r
a
dt
d
dt
d
(5.50)
e
V
VrVr
dt
rd
dt
rd
dt
rd
V
ree
r
aaa
0
0
, (5.51)
где
dt
rd
V
r
r
и
dt
rd
V
a 0
0
;
,2
0
0
r
a
dt
Vd
a
Vrr
dt
d
dt
Vd
V
dt
Vd
r
V
dt
rdr
r
dt
Vd
dt
Vd
dt
Vd
a
rr
reee
eaa
re
rr
ee
ee
caaa
c
r
(5.52)
где
,
e
a
,
c
a
r
a
соответственно переносное, кориолисово и относитель-
ное ускорение.
