Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.


4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3. Основные кинематические элементы движения жидкости
Гидрогазодинамика. Учеб. пособие 71
где а
некоторая константа.
В безвихревом потоке циркуляцию скорости выразим через потенциал
скоростей, поскольку
ddxVdxVdxV
332211
, т. е.
K
KK
d
21
,
где
1
K
и
2
K
– значения потенциальной функции на концах рассматри-
ваемого контура.
Течение жидкости в данном случае является плоским, установившимся
и, т. к.
2
1
1
2
x
V
x
V
(т. е. 3 = 0), потенциальным (безвихревым). При этом по-
тенциал φ можно определить по скорости потока
raxxaVVV //
2
2
2
1
2
2
2
1
,
где r
полярный радиус
точки (рис. 4.15
). Угол
находят
из соотношения
.
сos
2
2
22
r
x
a
r
r
ax
V
V
Отсюда следует, что вектор
скорости
V
перпендикулярен по-
лярному радиусу точки, т. е.
,0
r
V
SrSr
a
VV
S
1
Проинтегрировав последнее
уравнение, найдем
a
.
Этому значению соответствует функция тока
ra ln
.
Отсюда уравнение линий тока:
Cra
ln
. Согласно этому уравне-
нию, такие линии представляют собой окружности
C
r
с центрами в начале
координат.
Найдем циркуляцию скорости:
Рис. 4.15
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3. Основные кинематические элементы движения жидкости
Гидрогазодинамика. Учеб. пособие 72
2
0
2
a
ad
BA
AB
.
Если подсчитать величину этой циркуляции по любому замкнутому
контуру, охватывающему начало координат, то окажется, что
K
AA
d
1
.
Отсюда следует, что
2/a
. Физически этот случай, согласно теоре-
ме Стокса (см. ниже), соответствует наличию в особой точке
0r
вихревой
нити интенсивностью, равной циркуляции Г. При этом вне вихревой нити те-
чение будет безвихревое.
4
4
.
.
4
4
.
.
П
П
о
о
л
л
е
е
у
у
с
с
к
к
о
о
р
р
е
е
н
н
и
и
й
й
На основе функциональных связей (4.1)(4.2) можно получить общее
выражение для полного ускорения жидкой частицы. Ускорение – это вектор-
ная производная по времени от скорости.
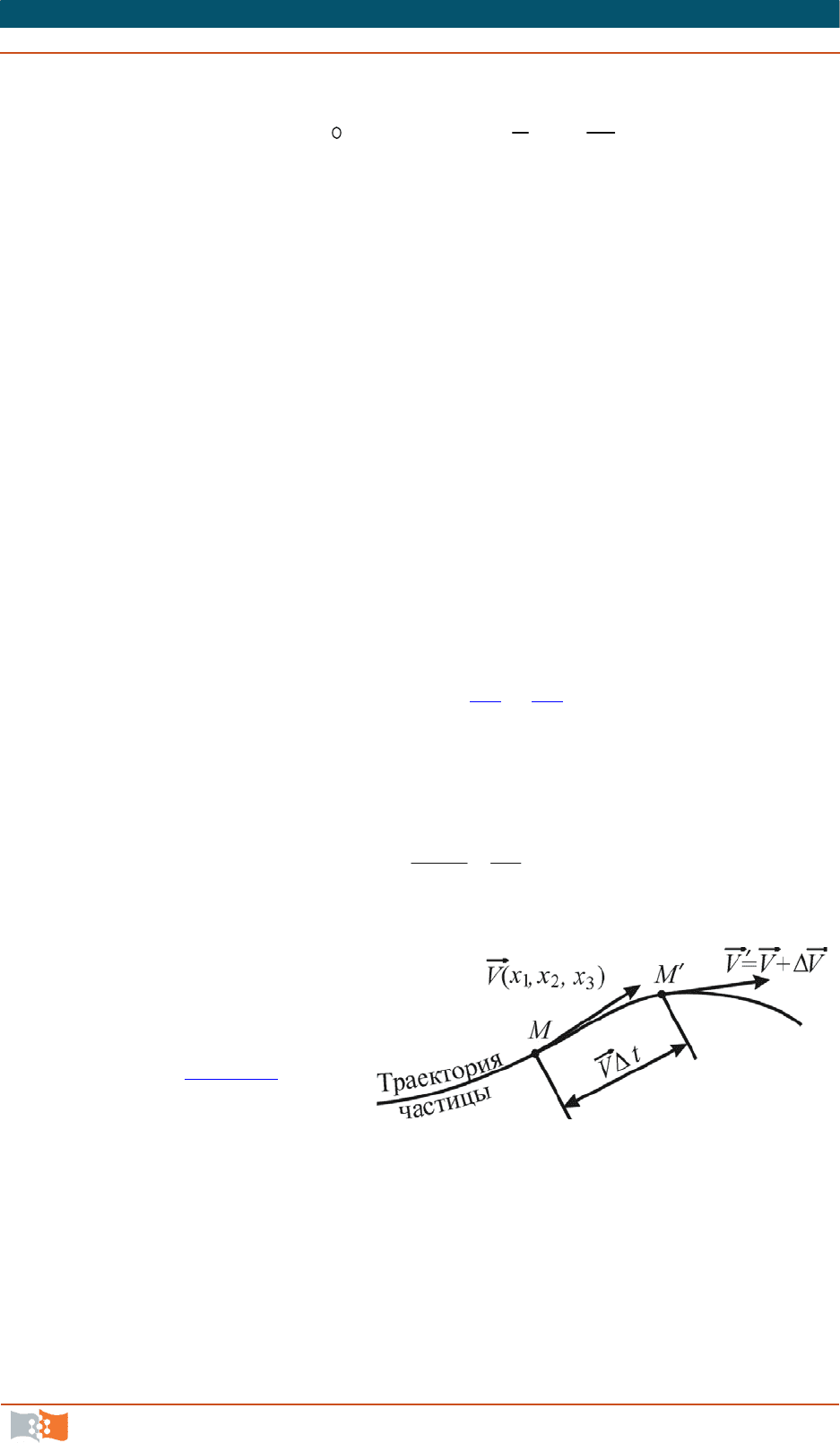
Известно, что ускорение перемещающейся фиксированной точки опре-
деляется пределом
,lim
0
dt
Vd
t
VV
t
где
V
,
V
скорости
частицы при ее перемещении
из точки
M
в точку
M
за
промежуток
t
(рис. 4.16).
В механике жидкости ус-
корение, определенное по ме-
тоду Лагранжа, выражается частной производной по времени
Рис. 4.16

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4. Поле ускорений
Гидрогазодинамика. Учеб. пособие 73
t
V
V
(точка над буквой обозначает производную по времени). Производная
t
V
выражает изменение скорости в фиксированной точке пространства,
т. к., по Лагранжу, переменные а, b, c в каждой точке разные. Здесь же в
конечном счете нужно знать, как изменяется скорость данной частицы
жидкости.
В эйлеровых переменных вектор скорости представляет собой в общем
случае вектор-функцию вектора-радиуса точек пространства и времени. Сле-
довательно, индивидуальную производную
dt
Vd
V
можно рассматривать как сложную функцию от времени
t
(нестацио-
нарное поле скоростей в явном виде) и через посредство координат х
1
, х
2
, х
3
движущейся точки. Тогда
,
3
3
2
2
1
1
dt
dx
x
V
dt
dx
x
V
dt
dx
x
V
t
V
dt
Vd
V
или, заменив
,
1
dt
dx
,
2
dt
dx
dt
dx
3
обозначениями проекции скорости на оси ко-
ординат
,V
dt
dx
,V
dt
dx
,V
dt
dx
3
3
2
2
1
1
получим
.
x
V
V
x
V
V
x
V
V
t
V
V
3
3
2
2
1
1
(4.7)
Спроецировав
V
на оси координат, имеем

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4. Поле ускорений
Гидрогазодинамика. Учеб. пособие 74
.
,
,
3
3
3
2
3
2
1
3
1
33
3
3
2
3
2
2
2
1
2
1
22
2
3
1
3
2
1
2
1
1
1
11
1
x
V
V
x
V
V
x
V
V
t
V
dt
dV
V
x
V
V
x
V
V
x
V
V
t
V
dt
dV
V
x
V
V
x
V
V
x
V
V
t
V
dt
dV
V
(4.8)
Введя вектор – дифференциальный оператор
321
321
xxx
и перейдя от проекции к векторному выражению, получим формализо-
ванное выражение ускорения
. VV
t
V
dt
Vd
V
(4.9)
Отсюда видно, что, по Эйлеру, ускорение можно разделить на две со-
ставляющие. Первое слагаемое
t
V
выражает изменение скорости со време-
нем в точке, т. е. при фиксированных координатах, называется локальным ус-
корением и характеризует нестационарность поля скоростей. Локальное ус-
корение равно нулю в любой момент времени, если поле скоростей стацио-
нарно (в этом случае траектории частиц жидкости совпадают с линиями то-
ка) или когда в данной точке скорость достигает своего
максимального (или
минимального) значения.
Следует обратить внимание, что в эйлеровых переменных, даже когда
t
V
= 0, ускорение все же имеется. Примером может служить вода, текущая с
постоянной скоростью по кругу: ускорение есть и тогда, когда скорость в
данной точке не изменяется. Причина в том, что скорость воды в данный мо-
мент в другой момент будет иметь другое направление – это центростреми-
тельное ускорение.
Второе слагаемое в правой части выражения (4.9
) образуется за счет
изменения координат точки, соответствующего перемещению (конвекции) ее
в поле скоростей, и называется конвективным ускорением, которое характе-
ризует неоднородность поля. Конвективное ускорение
конв
0V
тогда и толь-
ко тогда, когда поле скоростей однородно, т. е. скорости во всех точках рас-
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4. Поле ускорений
Гидрогазодинамика. Учеб. пособие 75
сматриваемой области одни и те же (например в начале движения тела в
неподвижной жидкости).
В механике жидкости и газа оператор индивидуальной производной по
времени
...
......
V
tdt
d
, (4.10)
использованный в (4.9
) применительно к вектору скорости, может
применяться также к скалярным функциям (например температуре, плотно-
сти
и т. д.) и к тензорным величинам, связанным с движущейся частицей жидко-
сти. Выражение (4.10
) называют еще субстациональной производной, т. к.
она вычисляется при наблюдении за движением материальной частицы.
4
4
.
.
5
5
.
.
К
К
и
и
н
н
е
е
м
м
а
а
т
т
и
и
ч
ч
е
е
с
с
к
к
и
и
й
й
а
а
н
н
а
а
л
л
и
и
з
з
д
д
в
в
и
и
ж
ж
е
е
н
н
и
и
я
я
ж
ж
и
и
д
д
к
к
о
о
й
й
ч
ч
а
а
с
с
т
т
и
и
ц
ц
ы
ы
В отличие от твердого тела жидкость представляет собой деформируе-
мую среду, т. е. появляется дополнительная (по сравнению с «твердым те-
лом») скорость, обусловленная деформацией жидкого объема. Следовательно,
скорости в отдельных точках пространства, заполненного движущейся жидко-
стью, могут быть неодинаковыми как по величине, так и по направлению.
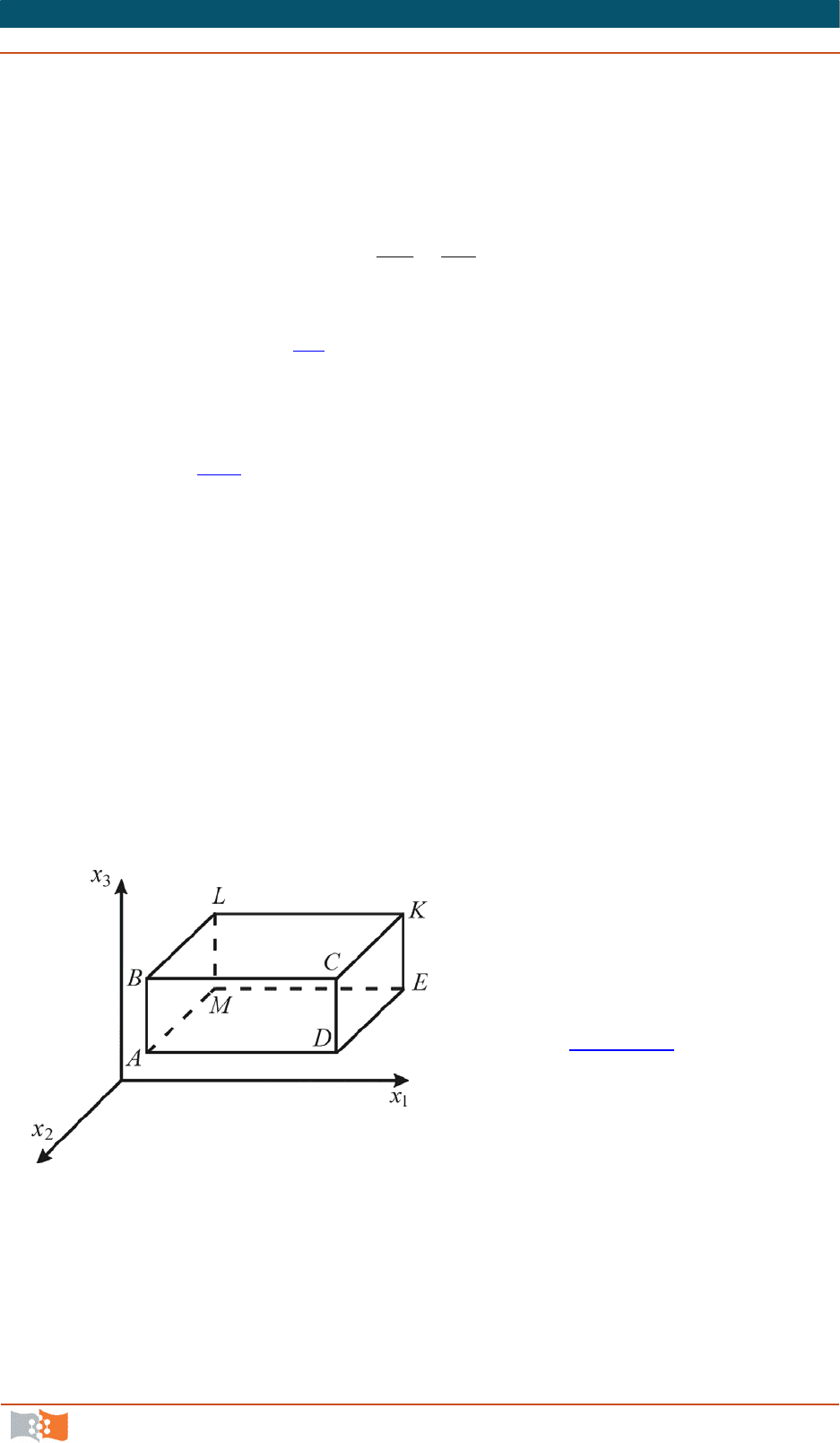
Пусть имеется некоторый
элементарный жидкий объем.
Начальную форму этого объема
удобнее всего представить в ви-
де прямоугольного параллеле-
пипеда
A
BCDEKLM , ребра ко-
торого параллельны осям коор-
динат (рис. 4.17
). Координаты
вершины
A
параллелепипеда
х
1
, х
2
, х
3
, а размеры его ребер –
dx
1
, dx
2
, dx
3
. Проекции вектора
скорости в вершине
A
паралле-
лепипеда обозначим V
1
, V
2
, V
3
. В
других вершинах за счет дефор-
мационного движения скорости
получают соответствующие при-
ращения:
Рис. 4.17

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5. Кинематический анализ движения жидкой частицы
Гидрогазодинамика. Учеб. пособие 76
1
1
1
dx
x
V
;
2
2
1
dx
x
V
;
3
3
1
dx
x
V
;
1
1
2
dx
x
V
;
2
2
2
dx
x
V
и т. п.
Проекции скорости в точке
D
можно записать следующим образом:
1
1
1
11
dx
x
V
VV
D
;
1
1
2
22
dx
x
V
VV
D
;
1
1
3
33
dx
x
V
VV
D
.
Проекции скорости в точке
B
3
3
1
11
dx
x
V
VV
B
;
3
3
2
22
dx
x
V
VV
B
;
3
3
3
33
dx
x
V
VV
B
.
Для точки С получим проекции скорости
С
V
3
3
1
11
x
x
V
VV
DC 1
1
1
1
dx
x
V
V
+
3
3
1
dx
x
V
;
3
3
2
22
x
x
V
VV
DC 1
1
2
2
dx
x
V
V
+
3
3
2
dx
x
V
;
3
3
3
33
x
x
V
VV
DC 1
1
3
3
dx
x
V
V
+
3
3
3
dx
x
V
,
и, наконец, для точки
K
имеем
2
2
1
11
x
x
V
VV
CK 1
1
1
1
dx
x
V
V
+
2
2
1
x
x
V
+
3
3
1
dx
x
V
;
2
2
2
22
x
x
V
VV
CK 1
1
2
2
dx
x
V
V
+
2
2
2
x
x
V
+
3
3
2
dx
x
V
;
2
2
3
33
x
x
V
VV
CK 1
1
3
3
dx
x
V
V
+
2
2
3
dx
x
V
+
3
3
3
dx
x
V
.
Исследуем частные случаи движения и деформации рассматриваемого
элемента.
Параллельный перенос. В данном случае элемент, не изменяя своей
формы, перемещается поступательно, подобно твердому телу, и все его точки
поэтому имеют одинаковую скорость.
Объемная деформация. Этот вид деформации связан с удлинением
граней. За время
d
t
грань
A
D
удлиняется на величину
D
D
, равную
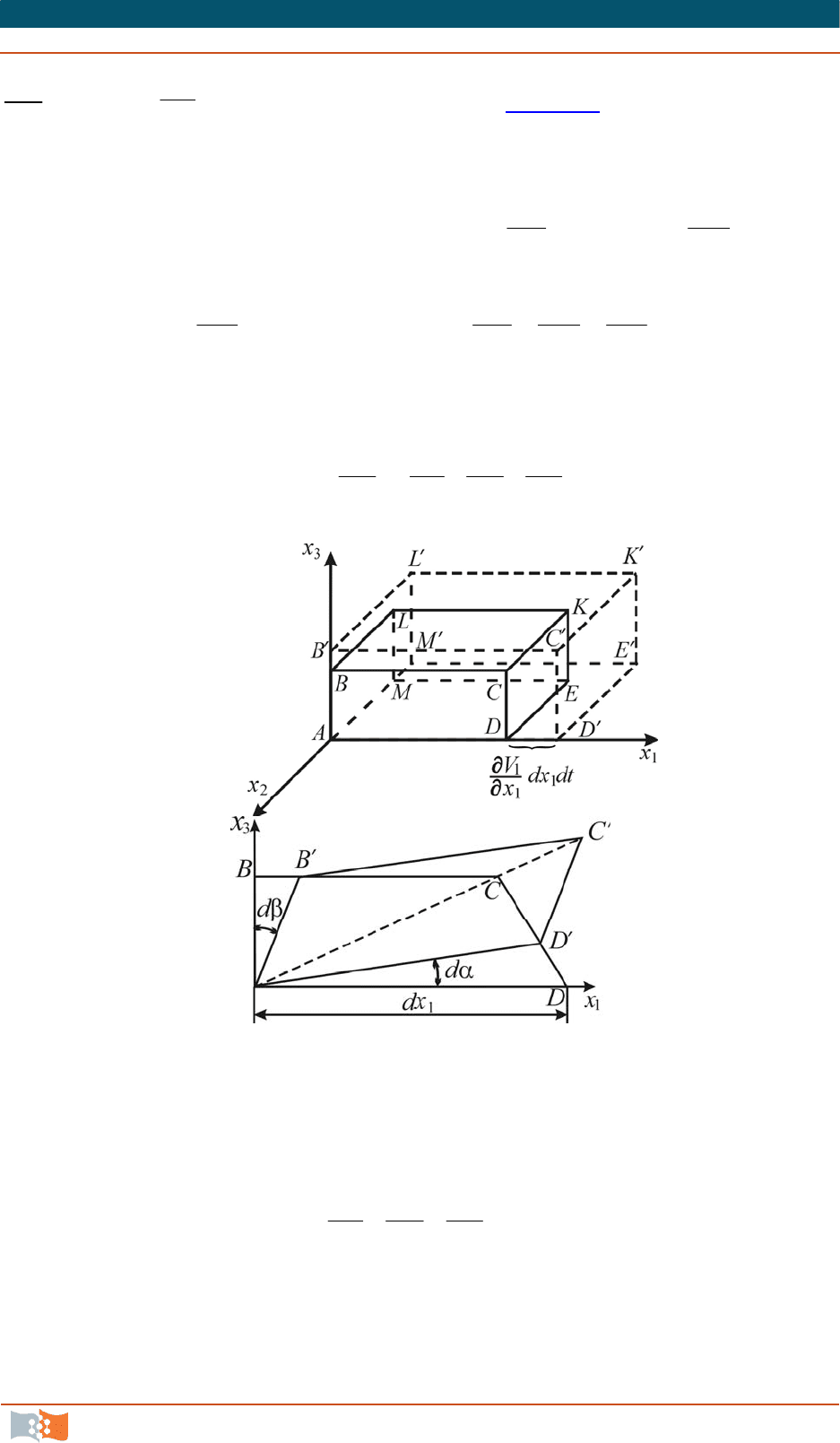
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5. Кинематический анализ движения жидкой частицы
Гидрогазодинамика. Учеб. пособие 77
dtdx
x
V
1
1
1
, где
1
1
1
dx
x
V
скорость деформации (рис. 4.18). Приращение объема
жидкого элемента
.
321
3
3
2
2
1
1
3213
3
3
3
2
2
2
21
1
1
1
dtdxdxdx
x
V
x
V
x
V
dxdxdxdtdx
x
V
dx
dtdx
x
V
dxdtdx
x
V
dxWWW
ABCDEKL
MLKEDCBA
Относительная объемная деформация
dt
x
V
x
V
x
V
dW
W
3
3
2
2
1
1
. (4.11)
Рис. 4.18 Рис. 4.19
Скорость относительной объемной деформации
V
x
V
x
V
x
V
div
3
3
2
2
1
1
.
Для несжимаемой жидкости
А

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5. Кинематический анализ движения жидкой частицы
Гидрогазодинамика. Учеб. пособие 78
0
3
3
2
2
1
1
x
V
x
V
x
V
. (4.12)
Уравнение (4.12
) представляет собой уравнение неразрывности для не-
сжимаемой жидкости.
Чистая деформация. Этот вид деформации обусловлен скашиванием
углов (рис. 4.19
). Грань AD повернется на угол dα. Поворот происходит
вследствие того, что скорость V3D точки D больше скорости V3A точки A
на величину
1
1
3
dx
x
V
. Тогда деформация DD´ равна
dtdx
x
x
1
1
3
. Вследствие
малости углов dα и dβ можно считать, что
dt
x
V
dx
DD
tgdd
1
3
1
,
dt
x
V
dx
BB
tgdd
3
3
3
.
Условие чистой деформации (скашивания углов)
d
=
d
, откуда
3
1
1
3
x
V
x
V
.
Скорость чистой деформации:
.
2
1
плоскости в
;
2
1
плоскости в
;
2
1
плоскости в
3
2
2
3
3223
32
2
1
1
2
2112
21
3
1
1
3
1331
31
x
V
x
V
SS
xx
x
V
x
V
SS
xx
x
V
x
V
SS
xx
(4.13)
Квазитвердый поворот.
В этом слу-
чае элемент, не меняя формы, поворачива-
ется как твердое тело на некоторый угол
(рис. 4.20
). Скорость
B
V
точки
B
больше
скорости в точке
A
, поэтому происходит
поворот ребра
A
B
в положение
B
A
:
Рис. 4.20

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5. Кинематический анализ движения жидкой частицы
Гидрогазодинамика. Учеб. пособие 79
3
3
1
11
dx
x
V
VV
AB
.
Тогда
B
B
равно
dtdx
x
V
3
3
1
, а
DD
dtdx
x
V
1
1
3
. Вследствие малости
углов принимаем
;tg
1
3
1
dt
x
V
dx
DD
dd
.tg
3
1
3
dt
x
V
dx
BB
dd
Так как
d
=
d
при повороте, то
1
3
3
1
x
V
x
V
.
Соответствующий такому перекашиванию ребер поворот всей грани
А
BCD следует определять вращением ее средней линии – биссектрисы угла
BAD
. Угол, на который повернется биссектриса угла относительно перво-
начального положения, определяется полусуммой
dd
2
1
. Следовательно,
угловая скорость ее вращения и вращения всего интересующего нас жидкого
элемента будет:
.
2
1
: оси ноотноситель
;
2
1
: оси ноотноситель
;
2
1
: оси ноотноситель
2
1
1
2
33
3
2
2
3
11
1
3
3
1
22
x
V
x
V
x
x
V
x
V
x
x
V
x
V
х
(4.14)
Скорости
1
,
2
,
3
можно рассматривать как проекции некоторого
вектора
на координатные оси.
Вектор
, имеющий проекции
,2
11
,2
22
33
2
, является
вихрем
V
rot
с компонентами
3
2
2
3
1
x
V
x
V
;

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5. Кинематический анализ движения жидкой частицы
Гидрогазодинамика. Учеб. пособие 80
;
1
3
3
1
2
x
V
x
V
(4.15)
2
1
1
2
3
x
V
x
V
.
Таким образом, угловая скорость квазитвердого вращения
.rot
2
1
V
(4.16)
