Кулагин В.А., Грищенко Е.П. Гидрогазодинамика
Подождите немного. Документ загружается.

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Гидрогазодинамика. Учеб. пособие 81
4
4
.
.
6
6
.
.
Д
Д
в
в
и
и
ж
ж
е
е
н
н
и
и
е
е
ж
ж
и
и
д
д
к
к
о
о
с
с
т
т
и
и
в
в
л
л
о
о
к
к
а
а
л
л
ь
ь
н
н
о
о
м
м
о
о
б
б
ъ
ъ
е
е
м
м
е
е
.
.
П
П
е
е
р
р
в
в
а
а
я
я
к
к
и
и
н
н
е
е
м
м
а
а
т
т
и
и
ч
ч
е
е
с
с
к
к
а
а
я
я
т
т
е
е
о
о
р
р
е
е
м
м
а
а
К
К
о
о
ш
ш
и
и
Г
Г
е
е
л
л
ь
ь
м
м
г
г
о
о
л
л
ь
ь
ц
ц
а
а
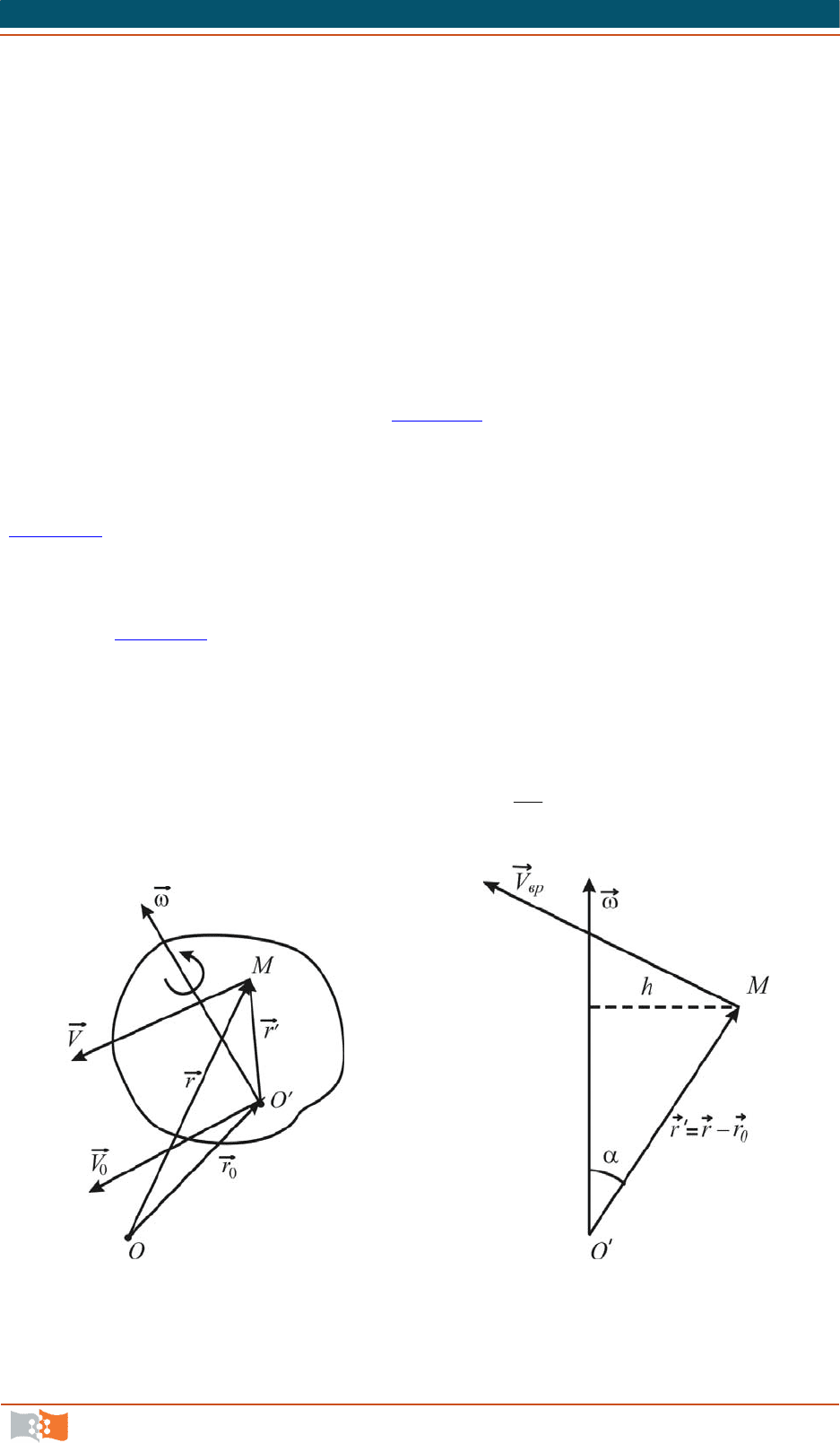
Из курса теоретической механики известно, что в общем случае дви-
жение твердого тела складывается из поступательного перемещения и вра-
щения вокруг мгновенной оси, проходящей через произвольно выбранный
полюс. Движение элементарного объема жидкости сложнее, так как, двигаясь
в сплошном потоке, он непрерывно деформируется.
Рассмотрим вначале квазитвердое движение жидкости, т. е. случай
движения воды, если ее заморозить до стадии льда. Вы
делим в жидкости
произ
вольный элементарный объем (рис. 4.21
) и разложим движение на состав-
ляющие. Особенностью квазитвердого движения является одинаковость угло-
вых скоростей всех точек тела независимо от выбора полюса и размеров тела.
Рассмотрим движение фиксированной точки
O
(полюса) твердого тела
(рис. 4.21
) и произвольной точки
M
заданными радиусами-векторами
0
r
и
r
;
r
радиус-вектор точки
M
относительно полюса
O
. Очевидно, что
rrr
0
или
.
0
rrr
В каждый момент времени тело еще и поворачивается. Пусть
вектор
(рис. 4.21) есть угловая скорость в данный момент времени и пусть в
этот же момент точка
M
имеет скорость
V
, а точка
O
скорость
0
V
. Тогда
врпост
VVV
, (4.17)
где
.
0пост
dt
rd
VV
Рис. 4.21 Рис. 4.22

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 82
Скорость вращения
вр
V
точки
M
– это угловая скорость, умноженная
на радиус вращения
h (рис. 4.22):
sin
вр
rhV
. (4.18)
Скорость
rV
вр
и оси вращения
, следовательно,
.
0вр
rrrV
(4.19)
Тогда поле скоростей в твердом теле в общем случае его движения оп-
ределяет классическая формула Эйлера
.
00
rrVV
(4.20)
Рассматривая твердое тело как сплошную среду с определенным полем
скоростей, найдем выражение вектора угловой скорости через скорости этого
поля. Для этого запишем поле скоростей в проекциях и найдем
через ско-
рости отдельных точек. Проекции (4.20
):
.
,
,
0112022133
0331011322
0223033211
xxxxVV
xxxxVV
xxxxVV
o
o
o
(4.21)
Так как угловая скорость для всех точек твердого тела одна и та же, т.
е.
= const,
V
есть линейная функция координат х
1
, х
2
, х
3
. Составим произ-
водные от проекции скорости (4.21
):
.rot2
,rot2
,rot2
33
2
1
1
2
22
1
3
3
1
11
3
2
2
3
V
x
V
x
V
V
x
V
x
V
V
x
V
x
V
(4.22)
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 83
Дифференциальную операцию rot называют пространственной произ-
водной в векторном поле
и определяют проекциями, представляющими собой
комбинацию частных производных, записанных в левой части равенств (4.22
);
rot
V
называют ротором скорости, или вихрем. В рассматриваемом случае
движения твердого тела формулы (4.22
) можно записать в векторном виде
V
rot
2
1
. (4.23)
В общем случае деформируемой среды – жидкости понятие угловой
скорости для целого объема становится бессмысленным, и рассматривать
разложение движения жидкости можно только в малом, элементарном ее
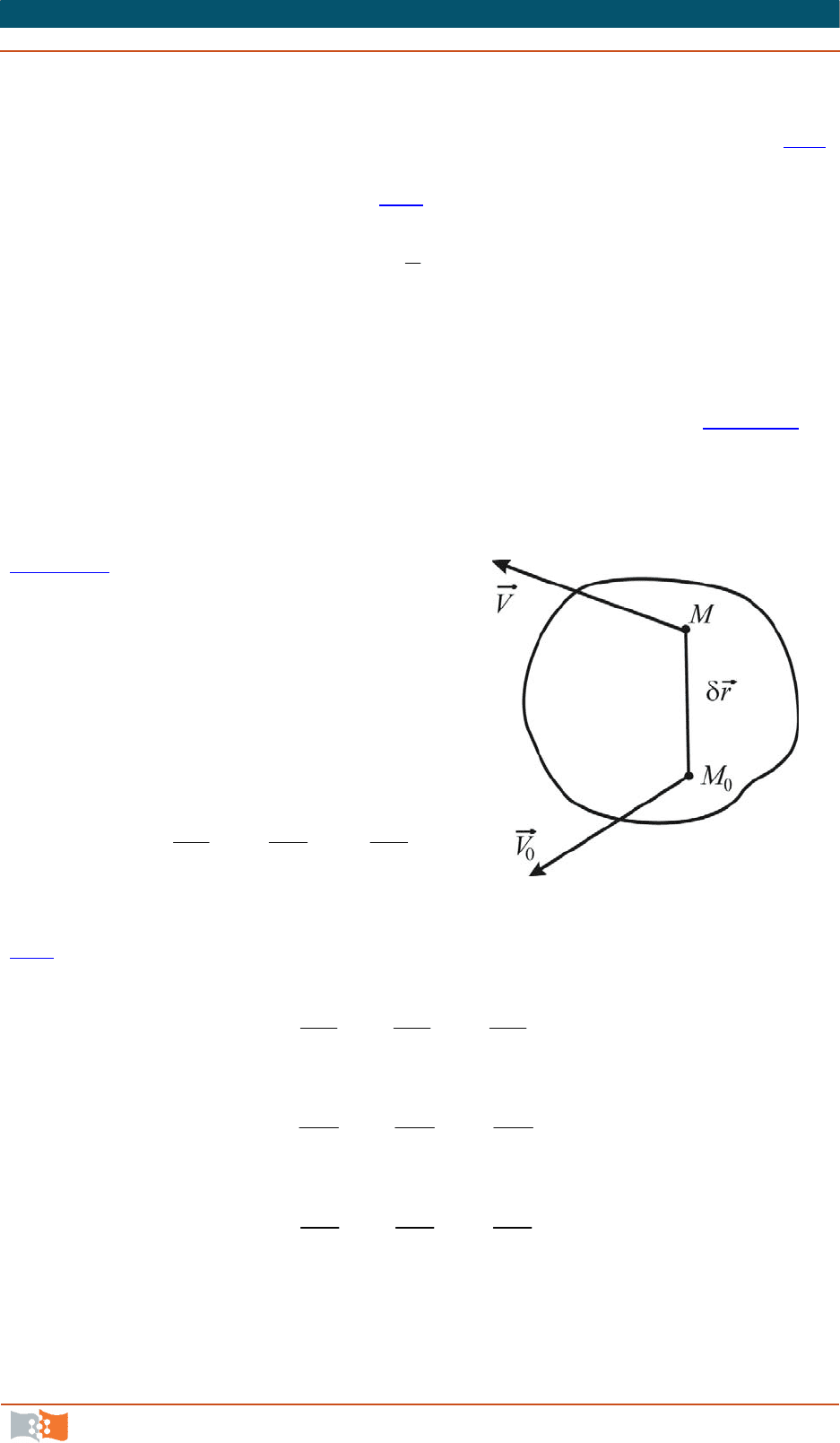
объеме в окрестности данной точки
M
(в локальном объеме рис. 4.23). В
случае локального объема поле скоростей в нем можно приближенно считать
таким же, как в твердом теле.
Примем за полюс точку
0
M
и рассмотрим движение частицы (матери-
альной точки)
M
, расположенной на бесконечно малом расстоянии
r
(рис. 4.23
). Знак
обозначает диффе-
ренциал в пространстве в данный фик-
сированный момент времени (прираще-
ние величины во времени обозначается
символом
d ).
В точке
М
,
00
VVVV
(4.24)
где
2
3
3
2
2
1
1
0
0x
x
V
x
x
V
x
x
V
VV
приращение скорости. Уравнение
(4.24
) без учета малых второго порядка в
проекциях будет иметь вид
.
,
,
3
3
3
2
2
3
1
1
3
33
3
3
2
2
2
2
1
1
2
22
3
3
1
2
2
1
1
1
1
11
x
x
V
x
x
V
x
x
V
VV
x
x
V
x
x
V
x
x
V
VV
x
x
V
x
x
V
x
x
V
VV
o
o
o
(4.25)
Переход от описания локальной деформации упругого твердого тела
(по закону Гука) к описанию деформации жидкой среды (по закону Ньютона)
Рис. 4.23

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 84
требует замены деформации упругого тела на скорость деформации, которая
является фундаментальным понятием движения жидкого объема.
Для выделения деформационного движения из (4.25
) вычтем компо-
ненты, составляющие квазитвердое движение:
.
,
,
1221тк
3113тк
2332тк
33
22
11
xxVV
xxVV
xxVV
ox
ox
ox
(4.26)
С учетом (4.22
) получим проекции скоростей деформационного движения:
,
,
,
333232131деф
323222121деф
313212111деф
3
2
1
xSxSxSV
xSxSxSV
xSxSxSV
(4.27)
где
;
1
1
11
x
V
S
;
2
2
22
x
V
S
;
3
3
33
x
V
S
;
2
1
1
2
2
1
2112
x
V
x
V
SS
;
2
1
2
3
3
2
3223
x
V
x
V
SS
.
2
1
3
1
1
3
1331
x
V
x
V
SS
Таким образом, движение жидкого объема характеризуется полем ско-
ростей:
;
дефтк
VVV
в проекциях:
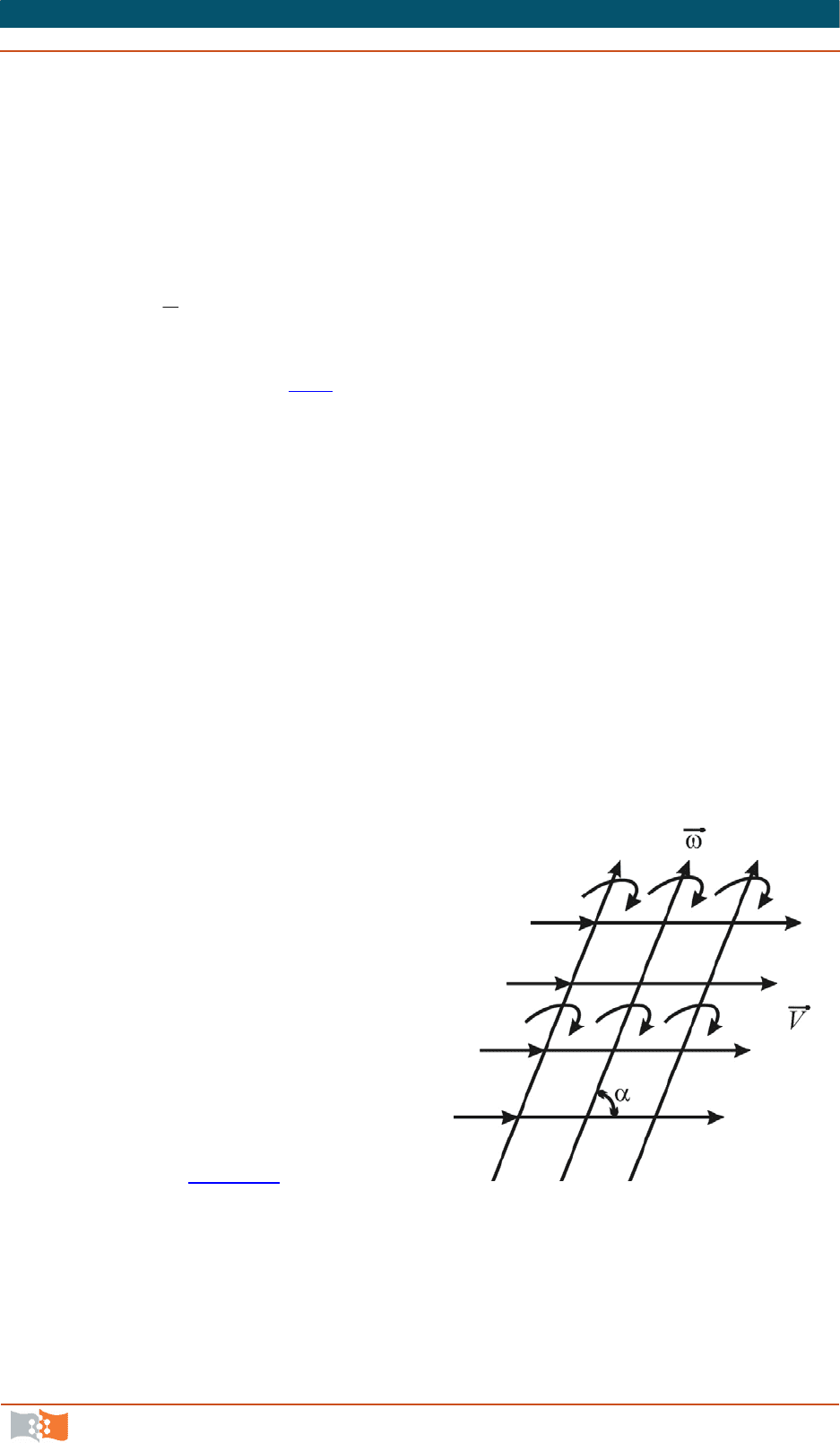
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 85
,
,
,
333232131122133
323222121311322
313212111233211
xSxSxSxxVV
xSxSxSxxVV
xSxSxSxxVV
o
o
o
(4.28)
где
322331132112
2
333
2
222
2
1110321
222
2
1
,,, xxSxxSxxSxSxSxStxxxS
функция деформации элемента объема, или тензор скоростей деформации.
В векторной форме (4.28
) записывают так:
,
0
rSrVV
(4.29)
причем первые два слагаемых выражают скорости в квазитвердом и
последнее – в деформационном движении, что соответствует первой кинема-
тической теореме Коши
Гельмгольца: движение элементарного объема
жидкости можно в каждый момент времени представить себе разложенным
на квазитвердое и деформационное.
Рассмотрим квазитвердое движение. В каждой точке поля скоростей име-
ем скорость поступательного движения и угловую скорость вращения частицы
жидкости, т. е. имеем поле угловых скоростей или поле вихрей (под вращением
частицы жидкости понимают поворот частицы вокруг мгновенной оси).
Метод Эйлера на
ряду с описанием поступательн
ого движения на осно-
ве понятия линии тока позволяет представить вращательное движение с по-
мощью понятия вихревой линии.
Вихревой линией называется линия,
в каждой точке которой вектор уг-
ловой скорости
направлен к ней
по касательной в данный момент
времени. Наглядным примером
вихревой линии может служить
гибкий вал.
Таким образом, движение ко-
нечного объема жидкости может
быть представлено совокупностью
семейства линии тока и семейства
вихревых линий (рис. 4.24
). Угол
может быть любым. В частности, при
совпадении линий тока и вихревых
линий возникает винтовое движение.
Если через каждую точку замкнутого контура по аналогии с трубкой
тока провести вихревую линию, то совокупность таких линий образует вих-
ревую трубчатую поверхность – вихревую трубку.
Рисунок 4.24

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 86
В деформационном движении три одноименные частные производные
,
1
1
x
V
,
2
2
x
V
3
3
x
V
в функции
S
(4.28) характеризуют скорость изменения вели-
чины единичного объема.
Сумма
1
1
x
V
2
2
x
V
3
3
x
V
V
div
(4.30)
называется дивергенцией (расхождением) вектора скорости. Равенство
0div V
является условием несжимаемости жидкости при const . С тече-
нием времени в этом случае изменяется только форма выделенного объема.
Оставшиеся слагаемые в правой части (4.28
) характеризуют скошение (сдвиг)
прямых координатных углов.
В гидромеханике различают движение без вращения элементов (потен-
циальное) и движение с их вращением (вихревое). В последнем случае из
теоремы Гельмгольца легко видеть, что вихри перемещаются вместе с жид-
костью со скоростью поступательного движения. С этим явлением можно
встретиться, наблюдая за кольцами табачного дыма или дыма, выходящего
из печной трубы: за
вихренность, види
мая из-за присутствия в потоке мелких
частиц продуктов сгорания, движется вместе с потоком нагретого воздуха.
Пример. Какие элементы характеризуют поступательное, вращатель-
ное и деформационное движение жидкой частицы в виде параллелепипеда,
скорость точки
С которой определяется в виде
233221231311111
dxdxdxSdxSdxSVV
C
,
где
;
1
1
11
x
V
S
1
3
3
1
13
2
1
x
V
x
V
S
;
2
1
1
2
12
2
1
x
V
x
V
S
;
1
3
3
1
2
2
1
x
V
x
V
;
21
3
12
1
.
2
VV
x
x
Деформационное движение жидкой частицы складывается из линейной
деформации, характеризуемой соответствующими коэффициентами
1111
/ xVS
;
2222
/ xVS
;
3333
/ xVS
,
и угловой деформации, определяемой величинами

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 87
;
2
1
3
2
2
3
23
x
V
x
V
S
;
2
1
3
1
1
3
31
x
V
x
V
S
,
2
1
2
1
1
2
12
x
V
x
V
S
т. е. полускоростями скашивания углов.
Поступательное движение жидкой частицы характеризуется скоростью
1
V
, вращательное – величинами
32
dx
и
23
dx
, деформационное –
111
dxS
,
313
dxS
и
212
dxS
.
Пример. Определить скорость относительного кубического расшире-
ния в потоке газа, проекции скорости которого заданы уравнениями
2
2
2
1
1
1
xx
cx
V
,
2
2
2
1
2
2
xx
cx
V
,
0
3
V
,
где
плотность газа; с векторная константа.
Относительная скорость кубического расширения частицы жидкости с
элементарным объемом
321
dxdxdx
определяется дивергенцией скорости:
3
3
2
2
1
1
div
x
V
x
V
x
V
V
.
Исследуемый поток плоский
0
3
V
и установившийся, следователь-
но,
.
111
1
div
2
1
1
2
2
2
1
2
2
2
2
1
2
2
2
2
2
1
2
2
2
1
1
2
2
2
1
1
2
2
2
2
1
2
1
2
2
2
2
1
1
x
x
x
x
xx
c
x
xx
cx
xx
xx
c
x
xx
cx
xx
xx
c
x
V
x
V
V
Пример. В двухмерном плоском потоке жидкости находится беско-
нечно малая частица в форме круга, уравнение которого
22
2
2
1
rxx
.
Какой будет форма этой частицы и как изменится ее площадь после
деформации, если деформация линейная и происходит вдоль осей
1
xO
и
2
xO
, являющихся главными осями деформаций?
Обозначим через
1
x
,
2
x
координаты, которые будет иметь точка
A
частицы через бесконечно малый промежуток времени
d
t
. Поскольку
1
xO
и
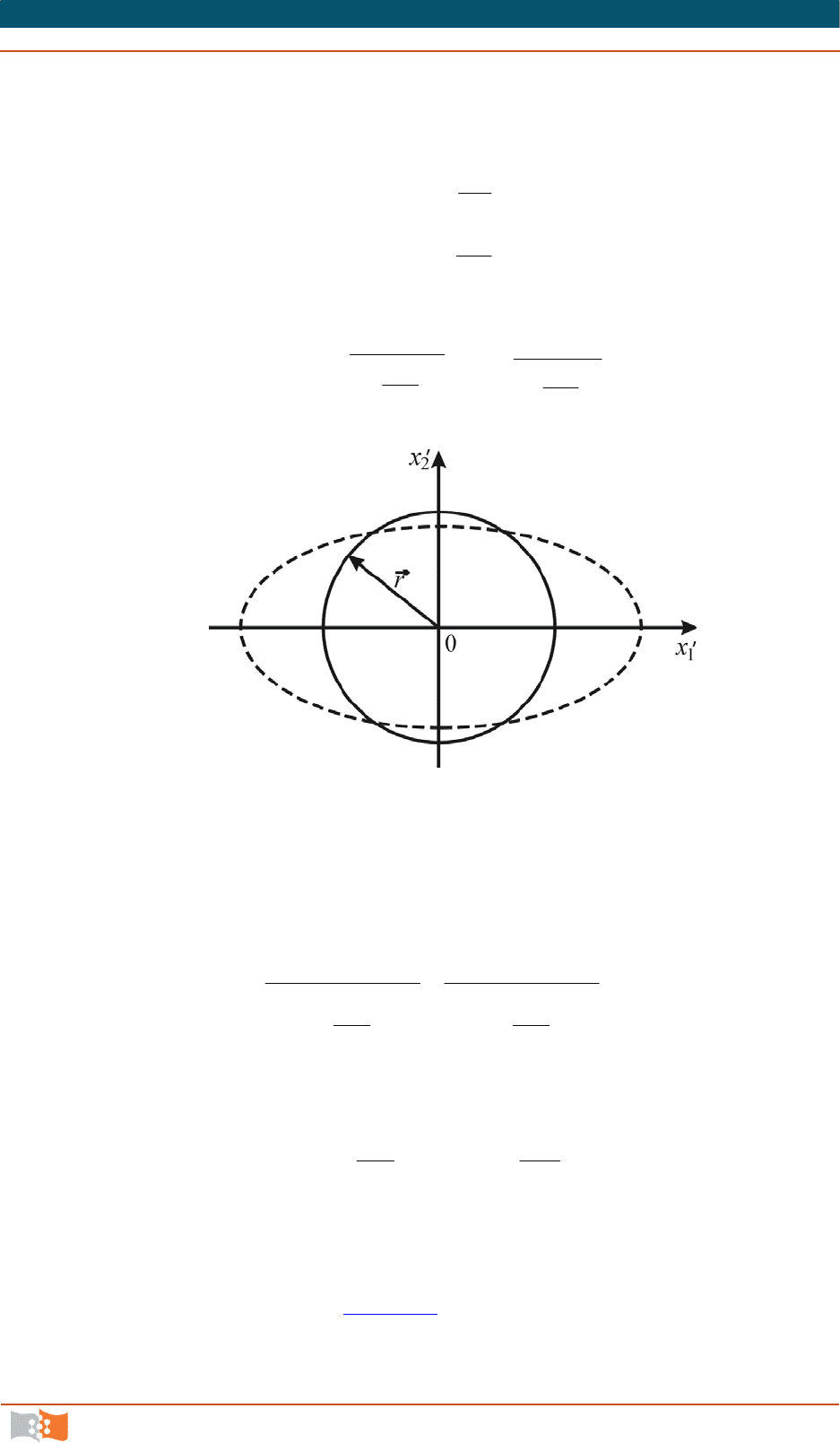
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6. Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Гидрогазодинамика. Учеб. пособие 88
2
xO
являются главными осями, то вдоль них имеют место только линейные
деформации и, следовательно,
dtx
x
V
xx
1
1
1
11
,
dtx
x
V
xx
2
2
2
22
.
Отсюда
dt
x
V
x
x
1
1
1
1
1
;
dt
x
V
x
x
2
2
1
2
1
.
Рис. 4.25
Подставляя значения
1
x
,
2
x
в уравнение заданной бесконечно малой
частицы в форме круга, найдем
1
11
2
1
1
2
2
2
2
1
1
2
2
1
dt
x
V
r
x
dt
x
V
r
x
.
Это уравнение является уравнением эллипса с полуосями
dt
x
V
r
1
1
1
и
dt
x
V
r
2
2
1
.
Таким образом, бесконечно малая частица в форме круга, деформиру-
ясь, обращается в бесконечно малый эллипс, оси которого направлены по
главным осям деформации (см. рис. 4.25
).
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Гидрогазодинамика. Учеб. пособие 89
4
4
.
.
7
7
.
.
У
У
р
р
а
а
в
в
н
н
е
е
н
н
и
и
е
е
с
с
е
е
к
к
у
у
н
н
д
д
н
н
о
о
г
г
о
о
р
р
а
а
с
с
х
х
о
о
д
д
а
а
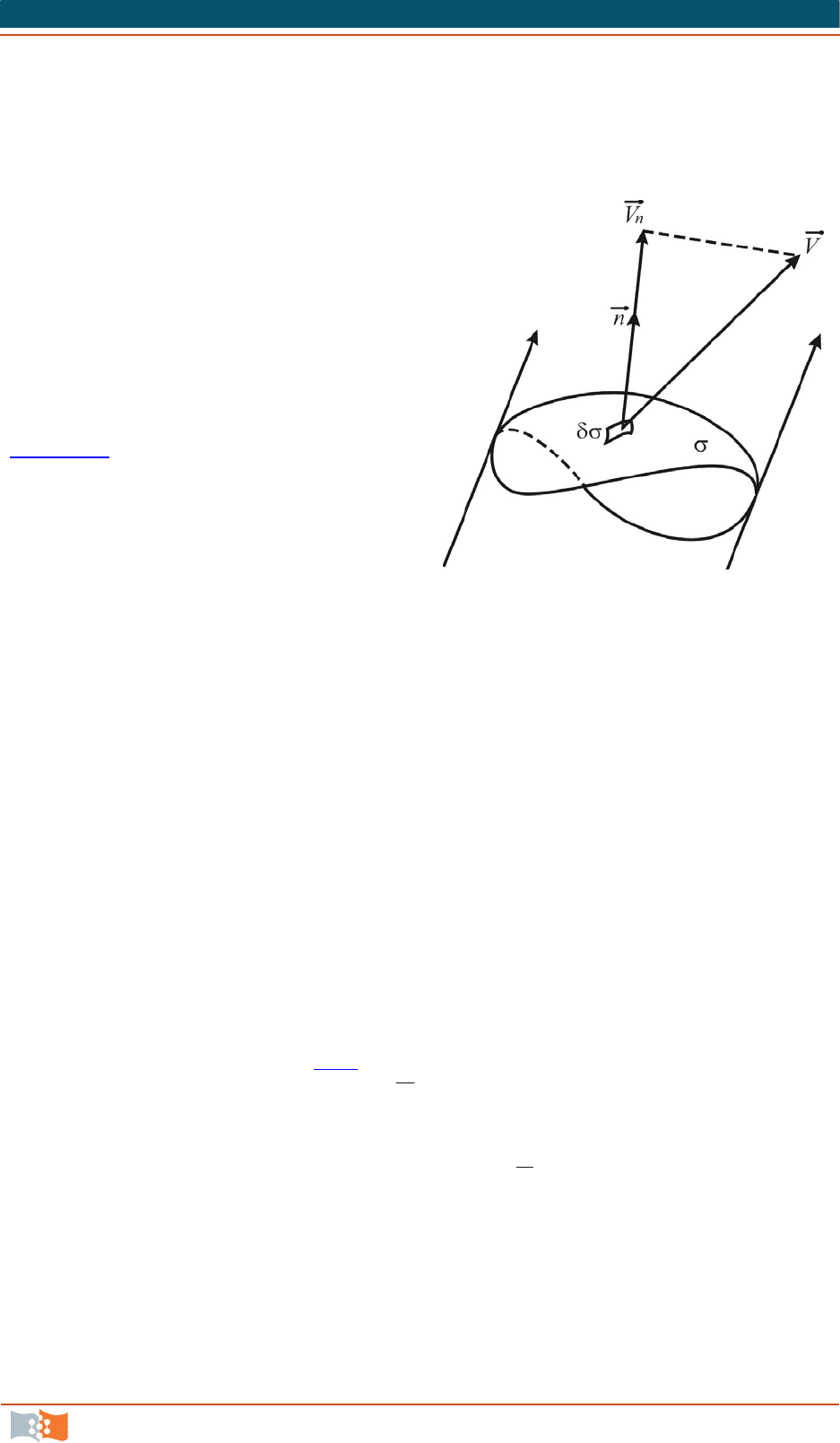
Рассмотрим простейший
случай секундного расхода жидко-
сти Q, протекающей сквозь по-
верхность σ, пересекающую труб-
ку тока, определяемого как поток
вектора скорости
V
. Выделим на
поверхности σ элементарную пло-
щадку δσ и отметим направление
нормали
n
к этой площадке
(рис. 4.26
). Сквозь поверхность σ
жидкость протекает с какой-то
скоростью
V
. Известно, что расход
дает только нормальная состав-
ляющая скорости
Vn. Тогда рас-
ход через элементарную площадку
δσ составит
n
VQ
. (4.31)
Секундный расход есть поверхностный интеграл
dnVVdVQ
n
cos
. (4.32)
При условии несжимаемой жидкости
const
n
VQ
(4.33)
вдоль данной трубки тока.
Используя уравнение (4.32
), получим практическое выражение для оп-
ределения объемной
Q
(массовой
m
) производительности (расхода) через
любое произвольное сечение потока:
,V
S
Q
или
VSm
. (4.34)
Здесь S
площадь проходного сечения, V
осредненная скорость по-
тока в этом сечении.
Рис. 4.26
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Гидрогазодинамика. Учеб. пособие 90
4
4
.
.
8
8
.
.
В
В
т
т
о
о
р
р
а
а
я
я
к
к
и
и
н
н
е
е
м
м
а
а
т
т
и
и
ч
ч
е
е
с
с
к
к
а
а
я
я
т
т
е
е
о
о
р
р
е
е
м
м
а
а
Г
Г
е
е
л
л
ь
ь
м
м
г
г
о
о
л
л
ь
ь
ц
ц
а
а
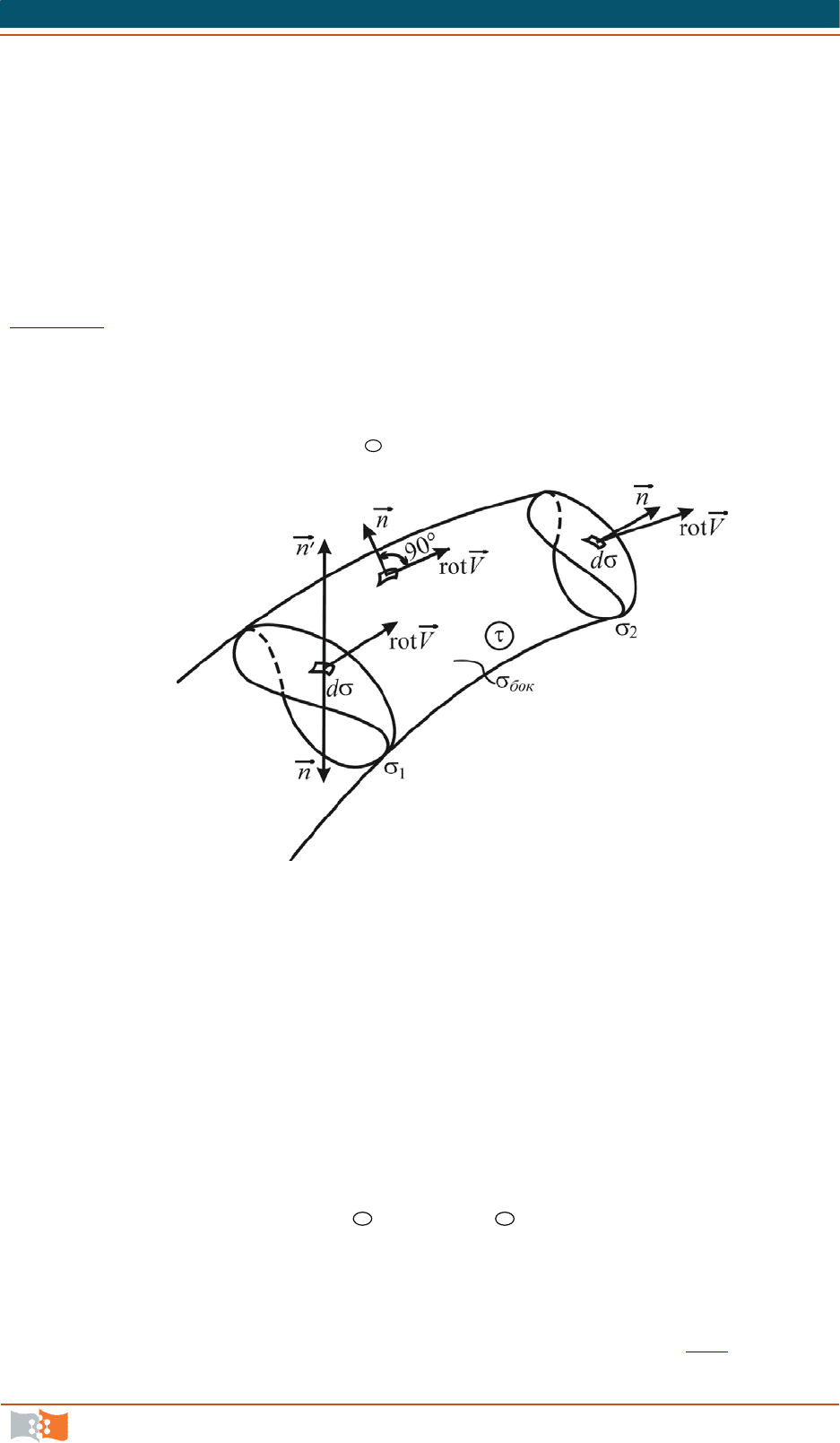
Эта теорема гласит: поток вектора вихря скорости сквозь произвольно
проведенное сечение вихревой трубки одинаков в данный момент времени
вдоль всей трубки, т. е. подобно тому как поток вектора скорости характери-
зует трубку тока, так поток вектора вихря характеризует вихревую трубку.
Для доказательства этой теоремы рассмотрим объем вихревой трубки τ
(рис. 4.27
), ограниченный боковой поверхностью σ
бок
и произвольными сече-
ниями σ
1
и σ
2
, запишем известное преобразование Остроградского Гаусса
для вектора
VQ
rot
:
ddn
. (4.35)
Рис. 4.27
Разобьем поверхностный интеграл на три части, соответствующие по-
верхностям
1
,
2
и
, tSVntSV
n
. Так как на боковой поверх-
ности
бок
n
, поверхностный интеграл по
бок
равен нулю, а следовательно,
тождественно равен нулю и объемный интеграл:
.0 rot divΩ VV
(4.36)
Тогда будем иметь
12
.0rot rot dVdV
nn
(4.37)
Для единообразного определения потока вектора сквозь сечение трубки в
направлении векторных линий заменим направление нормали в сечении
1
противоположным
n
. Тогда изменится знак первого слагаемого (4.37), получим
