Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

Подождите немного. Документ загружается.

5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ

5.8. Циркуляционное обтекание круглого цилиндра потенциальным потоком



Гидрогазодинамика. Учеб. пособие 121

ние, согласно уравнению Бернулли, меньше, чем на нижней, так что когда

на циркуляцию вокруг цилиндра налагается чистый горизонтальный поток,

возникает действующая на цилиндр вертикальная сила



, называемая подъ-

емной силой. В 1904 г. Н. Е. Жуковский установил, что подъемная сила про-

порциональна плотности жидкости, относительной скорости жидкости и

циркуляции, т. е.

 VF



. (5.82)

Выражение (5.82

) является частным случаем общей теоремы Жуков-

ского, относящейся к любому обтекаемому контуру.

При вращательном движении тел в потоке реальной жидкости можно

наблюдать возникновение циркуляционных движений. Эффект образования

при этом поперечной силы (эффект Магнуса, 1852 г.) помогает объяснить

многие интересные явления (отклонения «крученых» мячей в теннисе или

футболе, возникновение аэродинамического момента действия воздушного

потока на артиллерийский снаряд и т. д.). Изв

естн

а историческая попытка

применения эффекта Магнуса для создания судового движителя (А. Флет-

нер), состоящего из вертикальных вращающихся цилиндров, т. н. роторов

Флетнера, установленных на палубе судна для приведения в движение ко-

рабля энергией ветра.

При обсуждении обтекания потенциальным потоком цилиндра

(рис. 5.9

) считают, что жидкость скользит по поверхности твердого тела и

цилиндр в этом случае не испытывает сопротивления движению. Это утвер-

ждение неверно. В этом случае скорость на поверхности твердого тела может

иметь произвольное значение, и трение между жидкостью и твердым телом

не учитывается. Однако то, что скорость реальной жидкости совпадает со

скоростью той или иной точки тверд

го тела, в которой рассматривается те-

чение в данный момент времени (относительная скорость движения равняет-

ся нулю), – экспериментальный факт. Следовательно, решения для цилиндра

с циркуляцией жидкости и без нее не правильны. В реальной жидкости тре-

нием пренебречь нельзя. Результаты, полученные на основе модели идеаль-

ной жидкости, имеют вполне определенную погрешност

ь и ограниченность в

применении и зачастую носят лишь качественный характер.



Гидрогазодинамика. Учеб. пособие 122

В главах 1–5 рассматривалось поведение жидкости без учета эффектов

вязкости (внутреннего трения). При изучении идеальной жидкости иногда

делают еще одно приближение, считая жидкость несжимаемой, при этом по-

лучают дополнительное уравнение









Это приближение часто оказывается вполне целесообразным, особенно

когда скорость потока невелика. Но в реальных жидкостях внутренним тре-

нием пренебрегать нельзя. Некоторые жидкости, например глицерин, тяже-

лые масла и др., обладают очень большой вязкостью. Большинство практиче-

ски интересных явлений в жидкостях так или иначе связаны именно с этим

свойством. Вспомним важный экспериментальный факт – скорость жидкости

на поверхности твердого тела в точности равна нулю. Проиллюстрировать

этот факт (хотя не во всех случаях он очевиден) можно, если обратить вни-

мание, чт

о лопасти обычного бытового вентилятора собирают слой пыли, ко-

торая не сдувается, даже при вращении с довольно большой скоростью. Де-

ло в том, что скорость воздуха относительно них, измере

нная непосредст-

венно на их поверхности, равна нулю, так что поток воздуха не возмущает

даже мельчайших пылинок. По этой же причине можно сдуть с поверхности

стола крупные соринки, но не

мелкую пыль.

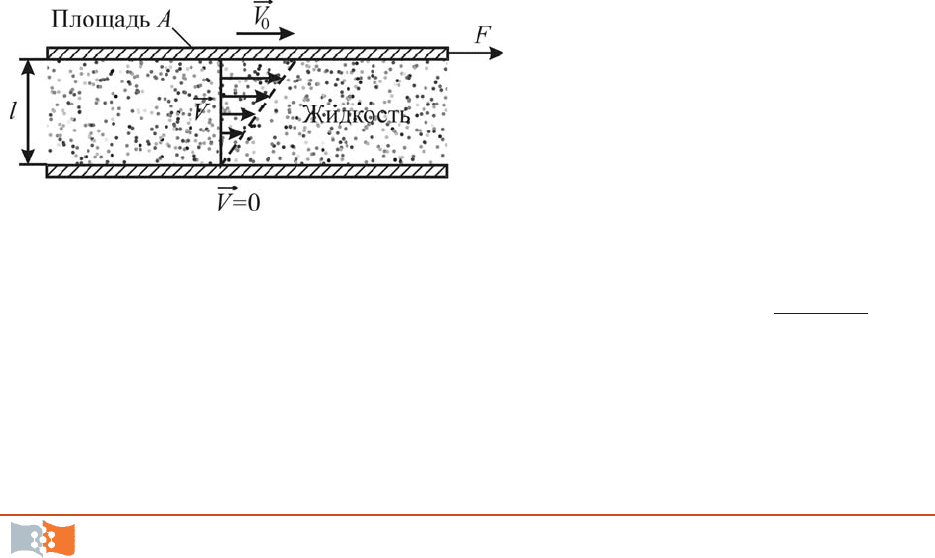
Чтобы понять, в чем за-

ключается сущность вязкости и

измерить силы, возникающие

при движении жидкости, рас-

смотрим такой эксперимент.

Пусть имеются две параллель-

ные пластинки, между которы-

ми находится

вода, одна из них

неподвижна, а другая движется

со скоростью

(рис. 6.1). То-

гда под действием вязкости в жидкости устанавливается такое движение, при

котором скорость слоев жидкости непосредственно около пластинок такая

же, какую имеют сами пластинки (слои воды «прилипают» к пластинкам).

Если измерить силу, требуемую для поддержания движения верхней пла-

Рис. 6.1

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.1. Вязкость



Гидрогазодинамика. Учеб. пособие 123

стинки, найдем, что она пропорциональна площади пластинки и отношению

, где l  расстояние между пластинками (рис. 6.1). Тогда напряжение сдви-

га

пропорционально



. (6.1)

Это выражение является частным случаем реологического уравнения

текучести обычной вязкой жидкости для простейшего случая прямолинейно-

го слоистого (ламинарного) движения, отвечающего известному закону Нью-

тона. Трение жидкости проявляется при этом в виде силы, оказывающей со-

противление движению верхней пластинки.

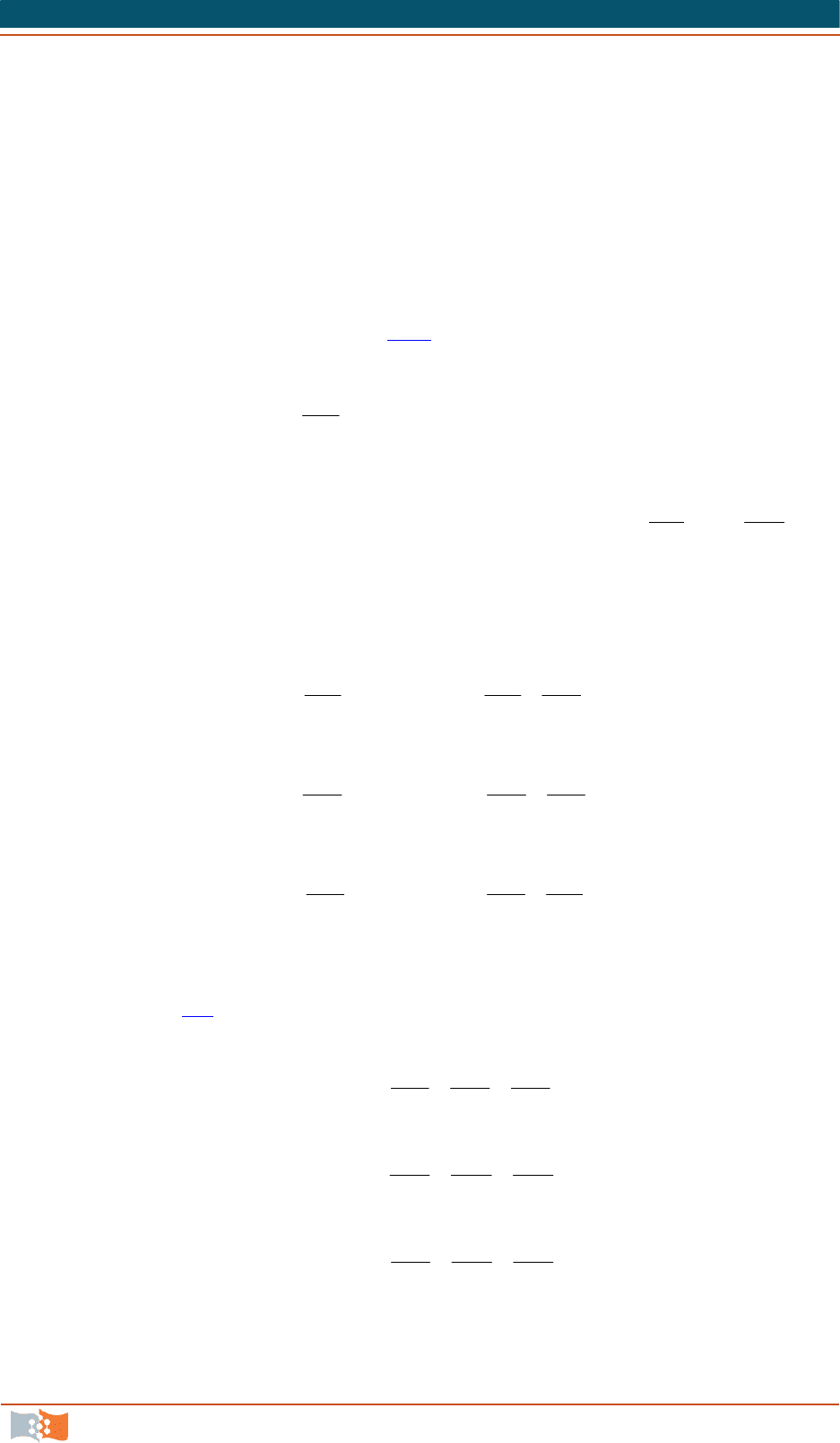
Для более сложного случая рассмотрим в жидкости небольшой пло-

ский прямоугольный объем, грани которого парал

лельны потоку (рис. 6.2).

Силы в этом объеме











(6.2)

где



 скорость изменения деформаций: силы в жидкости пропор-

циональны скорости изменения деформаций сдвига.

Явление «прилипания» к

твердым телам относится ко

всем жидкостям, а не только к

ньютоновским (так как при

больших градиентах бенгамов-

ские жидкости текут как ньюто-

новские, кроме того, у стенок

вообще самые большие градиен-

ты). Исключением может слу-

жить сильно разреженный газ

(свободный проб

ег молекул ко-

торого сопоставим с размерами

тела). Так, на больших высотах

(на высоте 100 км, например,

свободный пробег молекул раз-

реженного газа исчисляется в метрах) реактивный снаряд испытывает

ки-

нетическое

сопротивление от ударов отдельных молекул, а не обычное со-

противление трения.

Рис. 6.2

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ



Гидрогазодинамика. Учеб. пособие 124

Из общей теории трения жидкостей известно, что при деформации отдель-

ных элементов жидкости возникают напряжения такого же рода, как и в упругих

телах, только они пропорциональны не деформациям, а скоростям деформаций.

Уравнение движения вязкой жидкости получим, если к силам, дейст-

вующим в жидкости, в уравнении (5.19

) добавим сдвиговые силы (силы вяз-

кости)

вязк



вязк

grad fPF





. (6.3)

Компоненты напряжений сдвига пропорциональны пространственным

производным от различных компонент скорости, таких как



или



. По-

этому известные из теории упругости формулы для девяти компонент на-

пряженного состояния в случае жидкости принимают вид



















































































. ,2

, ,2

1331

3223

2112



(6.4)

Найдем силу вязкости

вязк



, действующую на единицу объема, и после

подстановки в (6.3

) получим уравнение движения реальной несжимаемой

жидкости. Компоненты силы вязкости:

















































(6.5)

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.2. Уравнение Стокса движения вязкой несжимаемой жидкости



Гидрогазодинамика. Учеб. пособие 125

Или в векторной форме (после подстановки (6.4) в (6.5) и соответст-

вующих преобразований):

вязк





(6.6)

где

xxx 













 оператор Лапласа. Подставив формулу (6.6) в

(6.3

), имеем уравнение

VPF





grad 

(6.7)

или



VPFVV





grad









которое называется уравнением Навье  Стокса; к нему еще присоеди-

няют уравнение несжимаемости

0 div V



и получают уравнения динамики

вязкой жидкости.

Уравнения динамики Стокса в проекциях записываются следующим

образом:





























































































































(6.7а)

Преобразуем уравнение (6.7) к более пригодному для применений ви-

ду, аналогичному уравнению Эйлера, в форме Громеки  Лэмба. Введя





, получим

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.2. Уравнение Стокса движения вязкой несжимаемой жидкости



Гидрогазодинамика. Учеб. пособие 126

VPFVV

























(6.8)

Полагаем, что единственными объемными силами являются консерва-

тивные силы типа сил тяжести. Чтобы понять физический смысл нового чле-

на, возьмем ротор уравнения (6.8

), тогда



















. (6.9)

Это напоминает уравнение (5.77), с той лишь разницей, что в правой

части имеется еще одно слагаемое. Если правая часть равна нулю, имеет ме-

сто теорема Гельмгольца о том, что вихри всегда движутся вместе с жидко-

стью. Если из (6.9

) исключим член









, то получим диффузионное урав-

нение. Новое слагаемое означает, что вихри диффундируют в жидкости.

Именно поэтому утолщаются кольца табачного дыма или дыма, выходящего

из печной трубы: вследствие вязкости вихри





диффундируют в окружаю-

щее пространство.

Совокупность уравнений (6.7а

) представляет собой замкнутую нели-

нейную систему уравнений в частных производных 2-го порядка с четырьмя

неизвестными: V

, V

и Р. Нелинейность системы обусловлена наличием

конвективных членов в левой части уравнений движения.

Для получения конкретных решений при интегрировании уравнений

(6.7а

) необходимо задать граничные и в общем случае начальные условия

(см. п. 5.3

). В отличие от идеальной жидкости здесь должно выполняться

граничное условие равенства нулю скорости жидкости на стенке, или совпа-

дения скоростей частиц жидкости со скоростями точек движущейся твердой

поверхности.

Рассмотрим теорию подобия двух течений как первый, общий вывод из

уравнений Стокса. Два потока жидкости называют подобными, если величи-

ны, характеризующие поток, могут быть получены из других соответствую-

щих величин, взятых в сходственных пространственно-временных точках,

простым умножением на одинаковые во всех точках коэффициенты подобия.

Вспомним условия подобия из геометрии. Два треугольника (

ABC







) подобны, если равны сходственные углы и отношение длин сторон

треугольников:

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.3. Механическое подобие потоков. Число Рейнольдса



Гидрогазодинамика. Учеб. пособие 127

idem











или, если измерить длины сторон в частях к.-л. стороны, например, АВ:

idem







и т. д.

Если вычислять физические величины в каких-то характерных масшта-

бах: скорости в масштабе скоростей, длины в масштабе длин, то два физиче-

ских явления будут подобны, если в сходственных точках различные пара-

метры жидкости могут быть получены в результате линейных преобразова-

ний с коэффициентами подобия или масштабными множителями.

Рассмотрим вопрос о подобии двух движений вязкой ньютоновской

несжим

аемой жидкости. Введем следующие обозначения: L  характерный

масштаб длин (диаметр трубы, длина обтекаемого тела), U  масштаб скоро-

стей (например осредненная по расходу скорость в трубе или скорость набе-

гающего потока), T



временной масштаб (в случае неустановившегося дви-

жения),

 масштаб сил,

– масштаб давлений;











будем считать по-

стоянными (изотермическое течение однородной жидкости).

Приведем уравнение Стокса к безразмерному виду. Для этого введем

следующие обозначения (штрихом обозначены безразмерные величины):







, или

,VUV







,tTt









PP



, х

соответствует

, , ,

321

xLxLxL



. Затем подставим эти значения в

(6.7

) и вынесем за знаки производных постоянные масштаба, получим



FFVV













































. (6.10)

Разделим все члены этого уравнения на

, тогда будем иметь















































. (6.11)

Предположим, что сравниваемые потоки жидкости подобны, тогда

уравнения, описывающие эти два движения, должны быть одинаковы. Но ве-

личины со штрихом по условию задачи в сходственных точках одинаковы.

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.3. Механическое подобие потоков. Число Рейнольдса



Гидрогазодинамика. Учеб. пособие 128

Остается, чтобы масштабные комплексы





были теми же

самыми. Отсюда необходимым условием подобия двух потоков вязкой не-

сжимаемой жидкости является одинаковость одночленных безразмерных

комплексов, которые называют «числами подобия», т. е.





















.idem

Фруда число

idem,Re

Рейнольдса число

idem,

Эйлера число

N где idem,

Струхала число

(6.12)

Те из чисел подобия, которые составлены из величин, заданных

наперед в постановке задачи (т. е. заданы начальными или граничными

условиями), называют критериями подобия; они определяют достаточ-

ные условия подобия. Весь набор условий подобия (подобие начальных

и граничных условий, равенства (6.12

) и т. д.) является необходимым

условием.

Рассмотрим такой пример, где в зависимости от постановки задачи

числа и критерии подобия могут меняться местами. Пусть жидкость движет-

ся сквозь трубу. Задан перепад давления



на длине

и известны плот-

ность



и кинематический коэффициент вязкости



. Требуется определить

расход

, или, иными словами, найти среднюю скорость

ср

. Пусть движение

стационарно. Числами подобия будут числа

Re и E

, но ни одно из них не

будет критерием подобия. Критерием в этом случае может стать такая ком-

бинация чисел

Re и E

, в которой не будет U:

ReEu







Из условия

idem

находим

ср

или

, т. е. число Re



















6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.3. Механическое подобие потоков. Число Рейнольдса



Гидрогазодинамика. Учеб. пособие 129

Если решать обратную задачу (известны Q(V

ср





, L; определить



), тогда здесь число Re







ср

критерий подобия, а число Eu

ср







 ис-

комое число подобия, т. к. является функцией Re.

Остановимся подробнее на рассмотрении числа











VLVL

которое характеризует отношение силы инерции к силе трения (вязко-

сти) и названо в честь английского ученого О. Рейнольдса, открывшего вы-

веденный закон подобия. Если число Рейнольдса мало, в потоке преобладают

силы вязкости. Наоборот, если число

велико, то главную роль в потоке

играют силы инерции.

Теория подобия служит для научного обоснования приемов моделиро-

вания действительных процессов в лабораторных исследованиях. В условиях

подобия модельного и «натурного» потока можно определить поведение

жидкости при обтекании подводного крыла или корпуса судна, не строя са-

мого корабля и не испытывая его. Вместо этого мож

но сделать модель и про-

вести опыты при скоростях потока, которые дают, например, то же самое

число Рейнольдса. Метод подобия позволяет применить результаты измере-

ний над малой моделью в гидродинамической трубе или бассейне для опытов

к настоящим объектам. Следует помнить, что это можно делать только при

условии, что сжимаемостью жидкости можно пренебречь. Кроме того, тео-

рия подобия является осн

овной теорией обработки экспериментальных дан-

ных. Эксперимент должен быть обработан в правильно выбранных характер-

ных масштабах, числах и критериях подобия.

Уже в 1839 г. Гагеном в экспериментах по изучению движения воды в

трубах малого диаметра и Пуайзелем (1841 г.) в опытах по исследованию

движения крови в капиллярных сосудах были установлены некоторые общие

закономерности движения жидкостей (зависимость скорости и расхода жид-

кости от температуры, физическая картина потока).

Ясность в вопрос о структуре потока в трубах при движении жидкости

в тех или иных условиях была внесен

а О. Рейнольдсом в опытах, проведен-

ных в 1883 г. Независимо от опытов Гагена, Рейнольдс проверил свои теоре-

тические исследования по изучению движения воды в трубах.

6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

6.4. Два режима течения вязкой жидкости



Гидрогазодинамика. Учеб. пособие 130

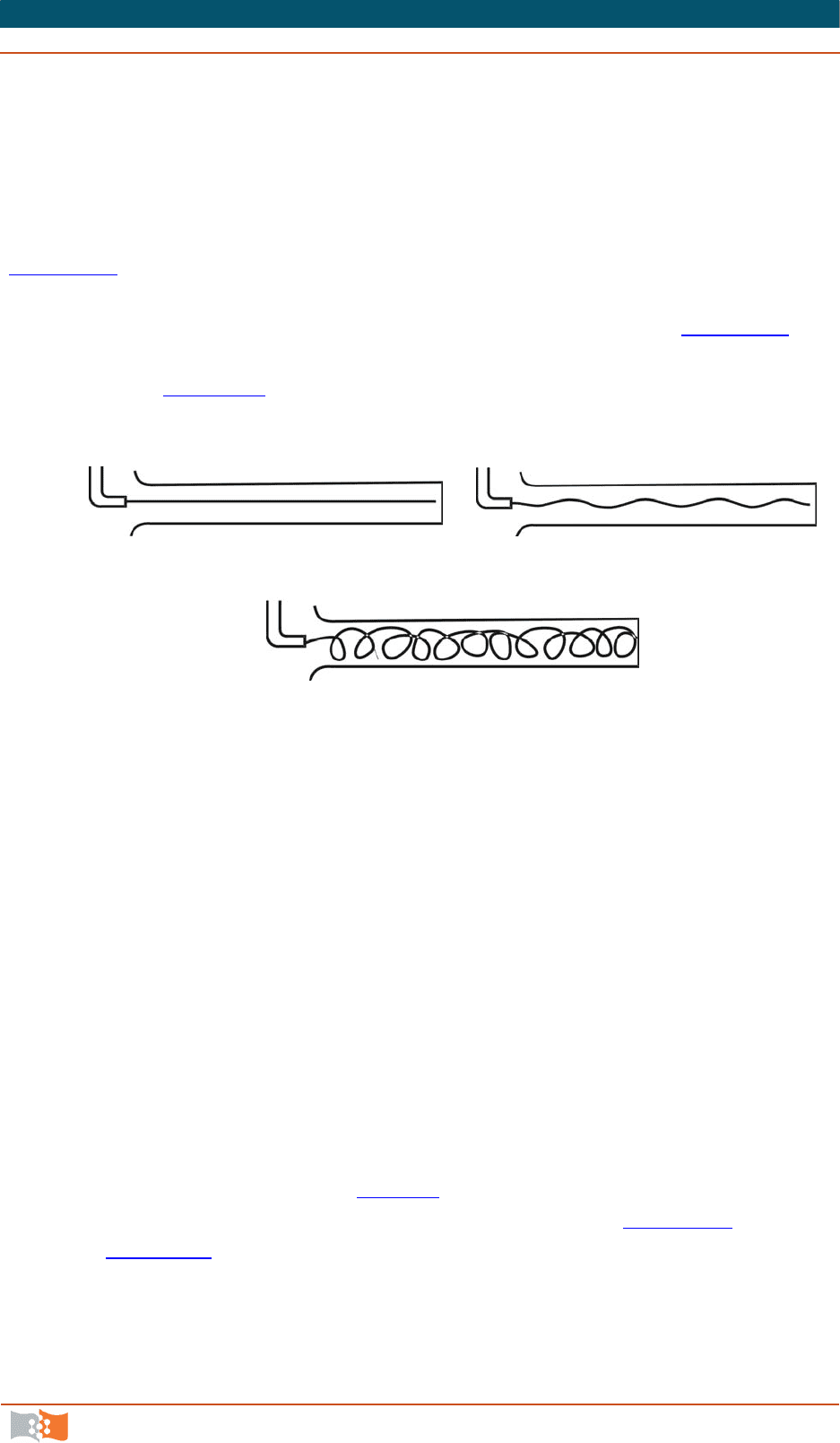
Схема опыта Рейнольдса проста и стала в настоящее время классиче-

ской. Наблюдалось течение воды в стеклянной трубке. Вода поступала из на-

порного бака и для визуализации структуры течения через специальную тру-

бочку в поток в начале трубки подавался раствор краски.

При малых скоростях потока (соответственно малых числах Re) окра-

шенная струйка текла приблизительно параллельно стен

кам трубы

(рис. 6.3, а

) на всем ее протяжении, т. е. имело место струйное, или слоистое

движение; такое движение называется ламинарным. При увеличении скорости

окрашенная струйка принимает вначале волнистые очертания (рис. 6.3, б

), за-

тем начинает пульсировать и почти внезапно исчезает, размываясь по всему

объему трубы (рис. 6.3, в

); такое движение называют турбулентным.

а б

Рис. 6.3

Переход от ламинарного режима движения в трубах к турбулентному

может происходить при разных числах предела: движение будет оставаться

ламинарным, если величина критического Re зависит от многих причин и,

прежде всего, от условий на входе в трубу. Опытным путем определено Re

кр

для нижнего предела: движение будет оставаться ламинарным, если Re < 2000,

т. е. нижнее Re

кр

= 2000. Верхнее значение Re

кр

в настоящее время не уста-

новлено. Структура потока в трубах определяет такие важные величины, как

сопротивление, теплоотдачу, характеристики перемешивания частиц, хими-

ческие процессы и пр. В связи с этим опыты по нахождению Re

кр

для специ-

фичных потоков в различных трубах продолжаются до настоящего времени.

Одновременно с переходом ламинарного течения в турбулентное изме-

няется распределение скоростей по сечению трубы, а также величина гид-

равлических сопротивлений. На рис. 6.4

показаны для сравнения эпюры рас-

пределения скоростей в круглой трубе при ламинарном (рис. 6.4, а

) и турбу-

лентном (рис. 6.4, б

) режиме движения.

При турбулентном течении распределение скоростей по сечению тру-

бы более равномерное. Это объясняется турбулентным перемешиванием

вследствие наличия поперечных составляющих скорости в отличие от лами-