Кухтевич В.И, Трыков Л.А., Трыков О.А. Однокристальный сцинтилляционный спектрометр (с органическим фосфором)
Подождите немного. Документ загружается.

61
в случае линейных спектров, показанных на рис. 2.7, с точностью до
экспериментальных ошибок, не наблюдается искажений в энергетических
распределениях, полученных с помощью выражения (2.8).
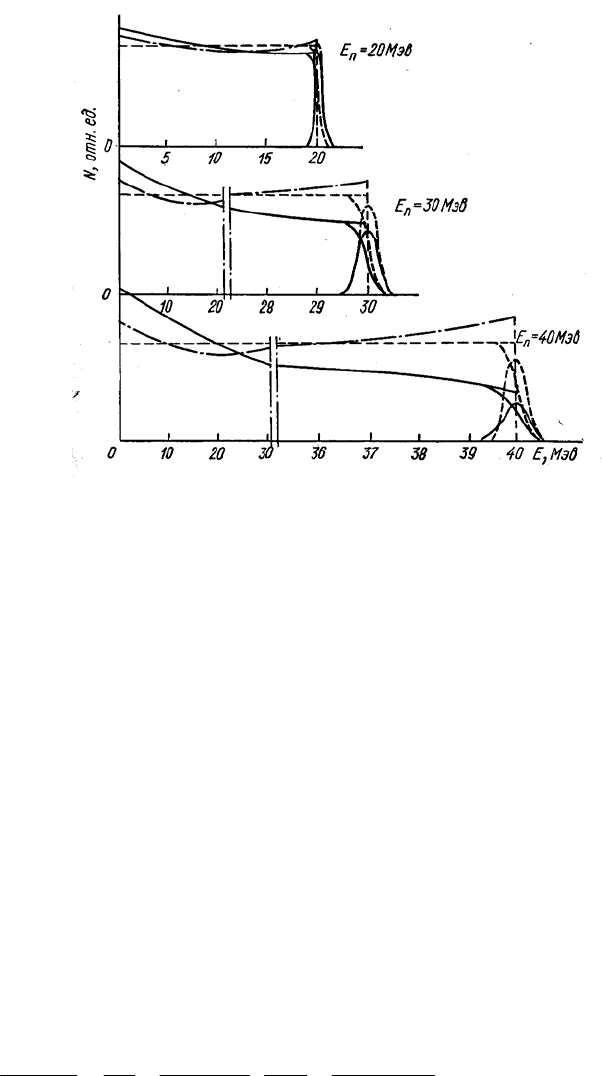
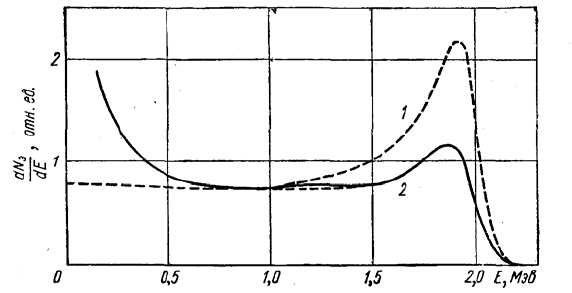
Рис. 2.8. Энергетические распределения протонов отдачи
(нелинейность световыхода учтена) для различных E
n
:
--------- dN/dE и Ф(Е); —.—.—.— dN/dE с учетом анизотропии (n,p) рассеяния; — — — — —
dN/dE и Ф(En) с учетом краевых эффектов (кристалл стильбена диаметром 30 мм и высотой 20
мм).
Сказанное о компенсирующей роли заштрихованной части кривой 3 на рис. 2.7
несправедливо для E
n
> 20 МэВ из-за особенностей, которые привносит в
распределение Ур )}/^Е р анизотропия рассеяния протонов отдачи в системе центра
масс в этой области энергий (рис. 2.8). Так обрабатывать амплитудные спектры по (2.8)
выше 20 МэВ можно без применения дополнительных приемов типа матричной
обработки [28], если размеры сцинтиллятора создают значительный краевой эффект
(по-прежнему
рассматриваются условия, обеспечивающие преобладание концевого
эффекта).Однако нивелирующая анизотропию роль краевого эффекта наступает при
таких размерах сцинтилляторов, при которых почти отсутствует многократное
рассеяние, а утечка столь велика, что практически сводится на нет компенсирующее
влияние факторов, указанных на стр. 66, 67. Поэтому для получения при помощи (2,8)
абсолютных значений dN(E
n
)/dE
n
необходимо вводить соответствующие поправки, т. е.
)(
)(
)(
)(
n
nn
p
pp
n
n
E
ECE
dE
dP
dP
EdN
dE
d
dE
EdN
ε
⋅
⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅⋅=
(2.32)
где С(Еп)—поправочный коэффициент, получаемый расчетным или
экспериментальным путем.
На рис. 2.8 приведено энергетическое распределение протонов отдачи
(нелинейность световыхода учтена) для E
n
, равной 20, 30 и 40 МэВ. Здесь же даны
61
62
расчетные распределения dN(E
p
)/dE
р
для кристалла стильбена толщиной h
= 2 см и
диаметром d
=
3
см. Расчет выполняли по формуле
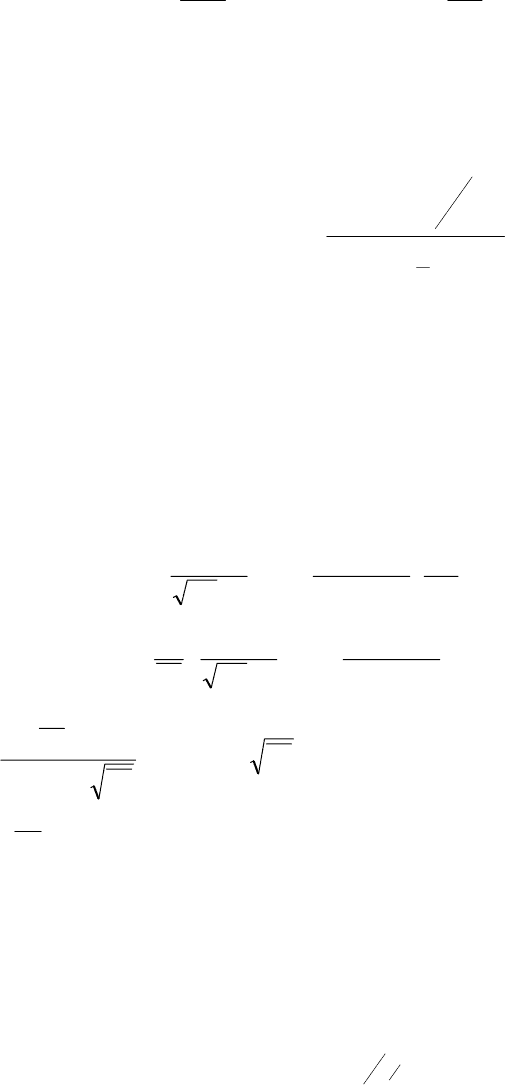
.),(),(
n
p
npnp
p
p
E
N
EEDEEA
dE
dN
=
(2.33)
Здесь А — поправка на анизотропию (n,р) - рассеяния; N
р
— общее число протонов
отдачи; D — величина, определяемая по выражению (2.27); A вычисляют по
следующему выражению:
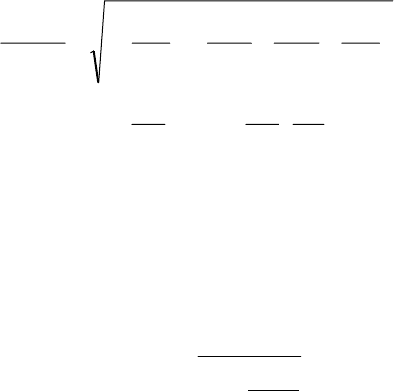
,
3
1
1
211
),(
2
b
E
E
b
EEA
n
p
np
+
⎟
⎠
⎞
⎜
⎝
⎛
−+
= (2.34)
где b = 2⋅(E
n
/90)
2
. Формула (2.34)—это полуэмпирическое выражение для области
14—42 МэВ [1]. Расчетные энергетические распределения протонов отдачи
размывались на конечное энергетическое разрешение спектрометра с помощью (2.35):
./ ADIdEdN
pp
=
(2.35)
В выражении
(2.35)
,
2
)(
exp
2
11
2
)(
exp
2
1
)(
0
2
2
0
2
2
pp
E
p
E
n
p
n
p
E
p
E
dEN
EE
E
dE
E
NEE
EII
∫
∫
∞
∞
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∆
−
−
∆
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∆
−
−
∆
==
π
π
(2.36)
где
.06356.0
10036.2
15
n
n
n
E
E
E
E
⋅=
⋅
⋅
=∆
Величина
n
E
соответствует энергии нейтронов, обозначенной на рис. 2.8 Е
n
.
Как видно из рис. 2.8, отличие d
2
N
p
/dE
2
p
от истинного распределения нейтронов
становится заметным уже при 20 МэВ, достигая С(Еn) ~ 25% при 30 МэВ (сравнение
выполнено для площадей под кривыми дифференциального распределения нейтронов).
В (2.32) множитель С(Е
n
) в области Е
n
< 20 МэВ хорошо аппроксимируется
эмпирической зависимостью
).1()(
2
3
225
E
n
eEC
−
+= (2.37)
Анизотропия
Авторы работы [1] для кристаллов стильбена и антрацена наблюдали существенное
изменение амплитуды импульса в зависимости от направления движения протона.
Кристалл с d = 12 и h = 12 мм облучали нейтронами с энергией Е
n
= 14 МэВ. Угол
62
63
между осью цилиндра и направлением пучка нейтронов поддерживали постоянным, а
азимутальный угол изменяли, вращая кристалл вокруг его оси. Изменения в амплитуде
импульса составили около 15%, и это выглядело так, будто происходило изменение
коэффициента усиления. Подобное наблюдали еще на трех кристаллах стильбена и
одном кристалле антрацена, и получили те же результаты. Если нейтроны
падают на
кристалл по направлению его оси, то при вращении кристалла изменения в амплитуде
импульсов не превышают 1%.
Авторами книги проведены аналогичные исследования для нескольких
коммерческих кристаллов стильбена отечественного производства с размерами от
d
=
10 мм, h
=
10
мм до d
=
70
мм, h
= 70 мм в интервале энергий нейтронов от 0,2 до
15 МэВ. Во всех случаях максимальный эффект анизотропии составлял 20%. Однако в
отличие от результатов работы [1], эффект анизотропии проявлялся с ростом
полярного, а не азимутального угла. Наибольшее значение анизотропии
соответствовало полярному углу 90°. Таким образом, анизотропию следует учитывать,
если в эксперименте изменяется направление
падения излучения. Примером может
служить измерение угловых распределений нейтронов в кольцевой геометрии. В
заключение следует добавить, что анизотропия кристалла стильбена возрастает с
увеличением порядкового номера падающей заряженной частицы. Так, в работе [19]
показано, что для α-частиц с энергией Е
α
= 6,93 МэВ анизотропия достигает 26%. У
пластических сцинтилляторов и сцинтиллирующих жидкостей этот недостаток
отсутствует.
§2.3. ОШИБКИ МЕТОДА
Ошибки преобразования амплитудных распределений нейтронов в энергетические
спектры в первом приближении можно оценить, рассматривая (в отношении
возможных ошибок) параметры, входящие в выражение (2.21). Относительную
ошибку преобразования по (2.21) можно записать в виде
dE
dP
dV
dP
VN
dV
d
Ф
Ф
P
X
EФ
p
Ф
x
P
x
n
x
⎥
⎦
⎤
⎢
⎣
⎡
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+++=
Φ
)(
,22
)(
'
2
2
2
'
2
2
2
2
2
'
ε
σ
σ
σ
σ
σ
ε
(2.38)
1. Величина σ
2
х
/х
2
характеризует точность градуировки энергетической шкалы
анализатора, которую проводят с помощью моноэнергетических γ-источников (см. 2.4)
по положению комптоновского «хвоста» электронов отдачи. Максимальная энергия
комптоновских электронов отдачи определяется по формуле
,
2
2
0
2
cm
E
E
E
макс
э
+
=
γ
γ
(2.39)
где Е
γ
, —энергия падающего γ-кванта, МэВ; m
0
c
2
=
0,511
МэВ— энергия покоя
электрона. В эксперименте положение E
э
макс
определяли по точке, соответствующей
0,6—0,7 высоты комптоновского спада характеристики аппаратурного распределения.
Эта точка соответствует максимуму производной в области комптоновского спада и
63
64
наиболее точно может быть определена по пересечению перпендикуляра,
восстановленного на энергетической шкале из точки E
э
макс
до пересечения с
комптоновским спадом характеристики, рассчитанной для соответствующей энергии γ-
квантов по формуле Клейна—Нишины—Тамма и размытой на энергетическое
разрешение спектрометра. Величина 0,6—0,7 получена для кристалла стильбена
размерами d
= 30 мм и h
= 20 мм с ФЭУ-13 при Е
γ
= 1 МэВ и несколько меняется с
увеличением энергии (до 0,5 для Е
γ
≈
4,5 МэВ) из-за стеночного эффекта.
Ошибка, связанная с градуировкой энергетической шкалы анализатора, обычно
редко превышает 2% и в основном зависит от стабильности электронной аппаратуры.
При хорошей стабильности всех электронных систем спектрометра эта ошибка может
быть сведена до 0,5%.
2. Величина σ
2
Px
/P
х
2
зависит от того, насколько точно известны значения функции
Р(Е). Выше были рассмотрены основные методы измерения и корректировки
световыхода Р(Е) сцинтилляционного спектрометра. При исследованиях функции Р(Е)
на электростатических генераторах суммарная ошибка всех факторов, влияющих на
точность значений Р(Е), составляет не больше 1—1,5% и может быть доведена в
области энергий 0,5—10 МэВ до 0,3—0,5%. Ошибки в определении Р(Е) методом
«известных сечений» несколько больше, но ,и в этом случае в среднем точность не
хуже 2—3% для Е
<
1 МэВ и 1—2% для Е
>
1
МэВ.
3. Величина σ
2
Ф’
/(Ф')
2
характеризует статистическую ошибку и часто (вместе с
систематической) является доминирующей. Статистическая точность величины Ф' тем
больше, : чем меньше осцилляции в амплитудных распределениях N(V), т.е. чем выше
статистическая точность N(V). Влияние осцилляций на точность результатов можно
уменьшить, если использовать метод наименьших квадратов [6,23] для
предварительного сглаживания, а затем и дифференцирования аппаратурных
распределений. Следуя этому методу, сначала ; ряду точек V
i
(где i
— номер канала
анализатора) ставят в соответствие некоторую кривую, например, вида
уi
= a
n
x
n
= а
0
+
а
1
x
1
+
а
2
x
2
+
а
3
х
3
.... Затем определяют коэффициенты a
n
удовлетворяющие условию минимума суммы квадратов разностей наблюдаемых
значений N(Vi) и расчетных y
i
по всему выбранному рассматриваемому интервалу. В
работе [23] приведена таблица коэффициентов а
n
для полиномов различной степени
(2—5), позволяющих выполнять сглаживание и дифференцирование
экспериментальных распределений на интервале с разным количеством точек i (от 5 до
25).
Согласно данным работы [23], сглаженное значение для N(V
i
) рассчитывают из
[
]
.)(
,
1
∑
−=
+
−
=
mj
jijmmi
VNaNP
(2.40)
В работе [23] приведены значения коэффициентов a
m,j
и нормировочных констант
N
m
-1
. Индекс т означает, что в расчете P
i
используется 2m+1 точек (каналов). При
этом задача состоит в том, чтобы: а) выбрать полином, который с наибольшей
точностью аппроксимировал бы экспериментальное распределение амплитуд, и б)
правильно выбрать величину интервала, т. е. т. В работе [24] изложено несколько
способов выбора т. Наибольшее внимание заслуживают два. По перовому способу
2m+1 выбирают равным или несколько
меньшим разрешения спектрометра в
рассматриваемом месте амплитудного распределения. Если N(V
i
)
< 100, необходимо
64
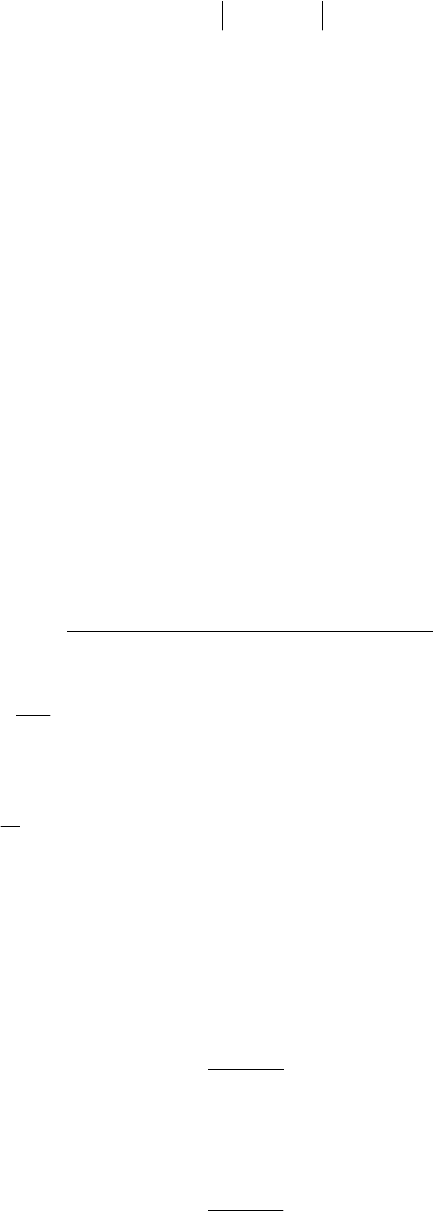
65
повторное сглаживание. По второму способу сразу выбирают 2m+1=25, так как
большее число точек не дает заметного эффекта. После сглаживания определяют
отношение
[
]
.)()(
2/1−
⋅−=
iii
VNPVNRi (2.41)
Исследование этого уравнения показало [24], что из статистических соображений
около 68% этого отношения должно быть меньше 1,0 и около 95% меньше 2,0. В тех
местах шкалы амплитуд, для которых после сглаживания Ri > 2,0, значение Pi
пересчитывается для интервала в 23 точки (2m+1=23). Если и этот раз Ri > 2,0, то Pi
пересчитывается для интервала в 21 точку,
и так до тех пор, пока Ri не станет меньше
2.
Во втором способе необходимо проводить повторное сглаживание, если N(V
i
)
<
25.
Для сведения к минимуму влияния осцилляций, которые еще могут проявляться
после операции сглаживания, можно воспользоваться методом сглаживающего
дифференцирования. Этот метод изложен в работах [6,23,25] и основан на тех же
принципах, что и обычное сглаживание. После того как выполнено предварительное
сглаживание, нет необходимости выполнять сглаживающее дифференцирование по
большому числу точек i. В
работе [6] достаточно полно проанализирована возможность
уменьшения влияния осцилляций применением сглаживающего дифференцирования
по пяти точкам в предположении, что аппаратурный спектр, умноженный на dV/dE, на
участке 5∆V (где ∆V – шаг дифференцирования) может быть представлен полиномом
второй степени. В этом случае формула для дифференцирования имеет вид
,
10
)(2)()()(2
2112
V
VFVFVFVF
iiii
i
∆
−
−
+
=Φ
′
++−−
(2.42)
где
,)()(
dE
dP
VNVF
i
ii
⋅=
а i -
номер канала, в котором определяется Ф
’
i
.
В большинстве случаев аппаратурные спектры наиболее точно описываются
выражениями типа
kV
e
V
−
1
и .
kV
e
−
В работе [6] показано, что аппроксимация экспериментальных распределений
полиномом второй или третьей степени на участке в 2k+1 точек (k – эквивалент
индексу m в операции сглаживания) несущественно сказывается на результате
сглаживающего дифференцирования (точность не хуже 1-2%), если выполняется
условие
.7,15,1
)(
)(
÷≤
−
i
ki
VN
VN
(2.43)
В рассматриваемом случае при k = 5 это условие запишется как
.7,15,1
)(
)(
2
÷≤
−
i
i
VN
VN
(2.44)
65

66
В случае, если преобразование аппаратурных распределений в энергетические
выполняется по (2.42), то в пренебрежении ошибкой функции dP/dE ошибка
дифференцирования запишется как
,)(
2
,
∑
=
−=
+
′
=
kb
kb
bibkiФ
DC
σ
(2.45)
Здесь D
i+b
– дисперсия набора в канале i; C
k,b
– эквивалент N
m
-1
a
m,j
в (2.40). При
проведении многократного сглаживания квадраты коэффициентов, входящих в общее
выражение для дисперсии, можно легко определить, воспользовавшись результатами
работы [23].
Основываясь на (2.45), можно выполнить запись для σ
2
Ф’
/(Ф’)
2
:
()
2
2
2
2
2
2
)
(
)(
)(
)(
dE
dP
dE
dP
Ф
Ф
Ф
i
i
Ф
σ
σ
σ
+
′
′
=
′
′
.
4. Величина
2
2
ε
σ
ε
. Отклонение эффективности (по протонам отдачи), рассчитанной
в приближении однократного рассеяния нейтронов, от действительной эффективности
кристалла, учитывающего другие взаимодействия, для энергий ниже примерно
12 МэВ составляет менее 0,5% [2,5,8]. Оказывается, что ε рассчитанное в однократном
приближении, применимо и для E > 12 МэВ, так как продукты побочных реакций не
являются протонами, а их вклад
ограничивается энергиями, меньшими 12 МэВ.
§2.4. ПРЕОБРАЗОВАНИЕ АМПЛИТУДНЫХ РАСПРЕДЕЛЕНИЙ В
ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ
γ
-ИЗЛУЧЕНИЯ
Известно, что органические сцинтилляторы можно успешно применять для
регистрации не только нейтронов, но и γ-излучения [26]. Однако, благодаря тому что
органические фосфоры обладают меньшей эффективностью и худшей разрешающей
способностью по сравнению с неорганическими сцинтилляторами, долгое время им
уделялось мало внимания.
Выделение импульсов от γ-излучения на фоне нейтронов (см. 1.5) изменило
отношение
к гамма- спектрометрам с органическими сцинтилляторами. Такие
спектрометры успешно применяются в различных экспериментах для измерений γ- и
нейтронных спектров и позволяют с помощью одного прибора определять суммарную
мощность дозы проникающего ионизирующего излучения (см., например, работы [26-
29]).
Для перевода амплитудных распределений в энергетические необходимо знать
форму линии спектрометра от моноэнергетических источников γ
-излучения. Основной
вид взаимодействия γ-квантов с кристаллом стильбена — это комптоновское рассеяние
на свободных электронах, и только при высоких энергиях фотонов часть
взаимодействий происходит в результате эффекта образования пар. Однако
66
67
распределение электронов отдачи в кристалле небольшого размера (форма линии
спектра) имеет сложный вид из-за многократного рассеяния γ-излучения и утечки
электронов за пределы кристалла.
Рис. 2.9. Энергетические распределения электронов отдачи, образующихся в результате
взаимодействия с кристаллом стильбена γ-квантов с энергией 2,23 МэВ: 1 — расчет в однократном
приближении без утечки электронов; 2 — экспериментальная форма линии спектрометра с
кристаллом стильбена 40X40 мм.
Расчет, проведенный в однократном приближении без учета утечки электронов,
показал, что расчетная форма линии отличается от экспериментальной (рис. 2.9).
Вследствие утечки значительной части высокоэнергетических электронов за пределы
кристалла происходит перераспределение импульсов в амплитудном распределении в
пользу более малых амплитуд Эффект многократного рассеяния γ-квантов, наоборот,
увеличивает количество импульсов с большими амплитудами.
Из
экспериментальных данных следует, что энергетическое распределение
электронов отдачи в первом приближении достаточно хорошо аппроксимируется
прямоугольным распределением вида dE/E
э
макс
(см., например, рис. 2.9, 2.10).
Поэтому преобразование амплитудных распределений импульсов в энергетические
распределения γ-квантов можно осуществлять дифференцированием. Но поскольку
распределение электронов отдачи отличается от прямоугольного распределения, то для
корректной обработки необходимо введение некоторой системы поправок. Достаточно
точно форму линии можно определить методом Монте-Карло, но и в этом случае
расчет значительно
затруднен из-за сложного характера траектории электрона отдачи в
кристалле.
В настоящее время наиболее надежно и быстро можно определить форму линии
спектра экспериментально, но и здесь имеется существенная трудность, связанная с
получением достаточно большого количества моноэнергетических источников γ-
излучения в широкой области энергий. В работе [28] для кристалла стильбена
диаметром 40 мм
и высотой 40 мм использовали набор из пяти моноэнергетических
линий: E
γ
= 0,661 МэВ (изотоп Cs
137
), Е
γ
= 1,12 МэВ (изотоп Zn
95
), E
γ
= 2,23 МэВ
(радиационный захват тепловых нейтронов ядрами водорода). E
γ
= 4,44 МэВ (γ-
излучение Ро — Ве источника, измеренное в совпадениях с нейтронами), E
γ
= 7,4 МэВ
[реакция Be
9
(p,γ)B
10
].
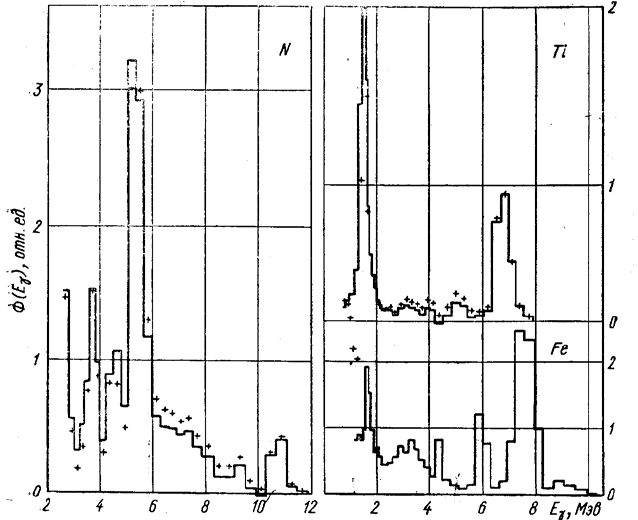
Были использованы также линии от γ-квантов с энергией 10,8 МэВ, возникающие
при радиационном захвате тепловых нейтронов ядрами азота.
67
68
Естественно предположить, что, благодаря изменению величины утечки
комптоновских электронов из органического сцинтиллятора, форма линии зависит от
размеров кристалла. Были измерены аппаратурные распределения и найдены
энергетические спектры γ-излучения от Ро — Ве источника для пяти различных
размеров кристаллов стильбена. Результаты измерений приведены в табл.
2.7.
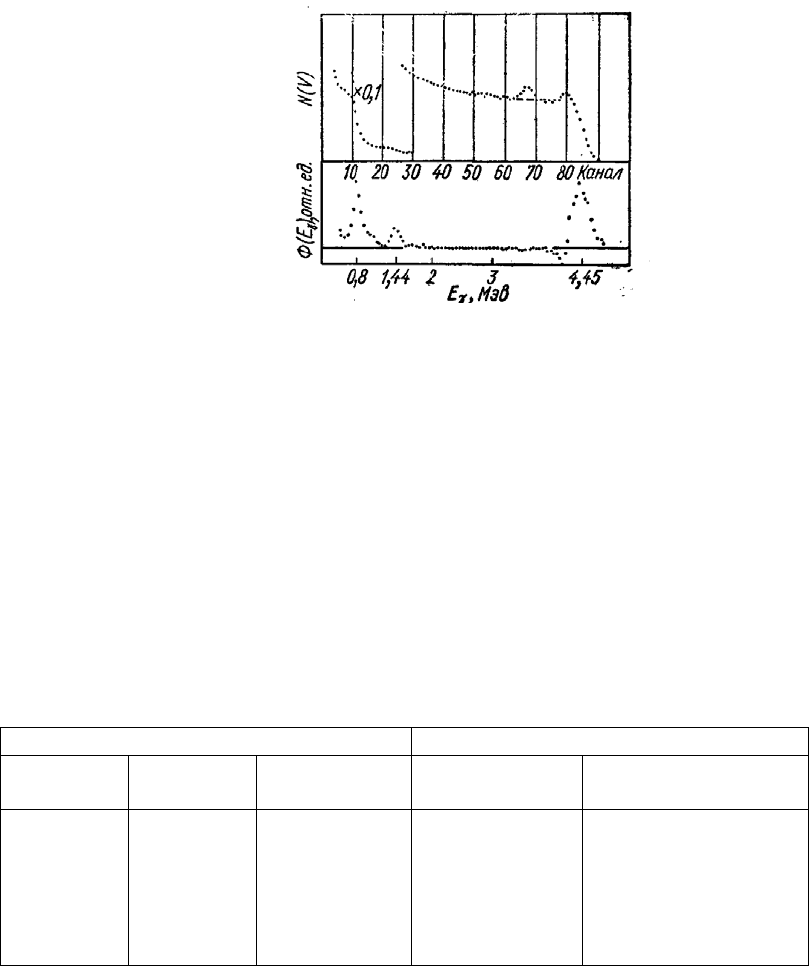
Рис. 2.10. Амплитудные и энергетические распределения у-квантов Ро — Ве-источника для
кристалла стильбена диаметром 40 мм и
Точность определения функций Ф'(Е
γ
) порядка 10%. Анализ полученных
результатов показывает, что хотя форма линий зависит от размеров кристалла, тем не
менее площади под пиками отличаются слабо до размеров кристалла стильбена d
= 30 и
h
=
20 мм и энергий Е
γ
= 4,44 МэВ (см. табл. 2.7).
Следует отметить, что различие в спектрах γ-излучения вызвано не только краевым
эффектом, но и разрешающей способностью кристаллов.
Таблица 2.7
Сопоставление функций Ф'(E
γ
) * для различных размеров кристаллов стильбена,
измеренных на Ро
— Ве источнике
Энергия
МэВ
Размеры кристалла стильбена
мм
0,8 1,44 4,43
D h
411 110 618 30 20
406
113
740
40
40
408
116
756
50
50
405 115 738 70 70
Ф'(E
γ
) = Ф(E
γ
)R
2
/Jt, где R — расстояние между центрами источника и кристалла; J —
чувствительность спектрометра с данным кристаллом стильбена; t — время
измерения.
Из рис. 2.10 также видно, что для энергий Е
γ
~ 5 МэВ эффект образования пар еще
не велик и может быть легко учтен. Аннигиляционный пик используют для
дополнительной проверки разрешающей способности спектрометра в области высоких
энергий
γ-квантов.
68

69
Корректировка энергетических распределений γ-квантов,. полученных методом
дифференцирования аппаратурных распределений импульсов, производится с
помощью числовой треугольной матрицы. Алгоритм преобразования амплитудных
распределений импульсов в энергетические распределения γ-квантов можно записать
следующим образом [28,29].
Амплитудное распределение импульсов N(V) преобразуем в энергетическое
распределение электронов отдачи N(E
э
) по, формуле
).()(
i
i
э
VANEN
=
(2.47)
Численно дифференцируя распределение электронов отдачи. N(E
э
) по энергии Е
e
и
учитывая «эффективность» регистрации
,
)(
)(exp(1
)(
макс
iэ
it
i
EK
tE
E
γ
γ
ε
Σ
−
−
=
(2.48)
где K(E
э
макс
) — аналог поправочного коэффициента С(Е
n
) в выражении (2.32),
получаем энергетическое распределение γ-квантов F(E
γ
) с искаженной энергетической
шкалой согласно выражению
511.0
2
1
i
i
i
макс
iэ
E
E
EE
γ
γ
γ
+
−=
или
,
02,1
11
2
5,0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++=
макс
iэ
макс
iэ
i
E
E
E
γ
(2.49)
где E
э
макс
— максимальная энергия комптоновских электронов отдачи, образуемых
в кристалле стильбена γ-квантами с энергией E
γ i
:
.
)(
22
)(
i
макс
iэ
iэ
iэ
iэ
iэ
iэ
i
E
E
E
E
EN
E
EN
EF
γ
γ
ε
⋅
∆
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∆
−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∆
+
=
(2.50)
Данное энергетическое распределение получено в предположении, что форма линии
спектрометра представляет собой идеальное распределение вида dE/E
э
i
макс
. Отклонение
реальной формы линии от идеальной учитывалось с помощью корректирующей
числовой матрицы.
Исправленное энергетическое распределение γ-квантов. Ф(Е
γ
i
) получаем согласно
выражению
).,()()()(
1
ij
n
ij
jii
EELEEFE
γγγγγ
∑
+=
⋅Φ−=Φ
(2.51)
69
70
Принятые обозначения в формулах (2.47) — (2.51) : A — энергетическая ширина
канала амплитудного анализатора,. канал/МэВ; К(E
э i
макс
) — поправочный
коэффициент, учитывающий краевые эффекты и определяемый из анализа
энергетических распределений комптоновских электронов отдачи, возникающих при
взаимодействии моноэнергетических γ-квантов с кристаллом стильбена:
∆
Е
э i
— энергетический шаг при численном дифференцировании, МэВ;
1-exp[-
Σ
(E
γ
i
)t] — эффективность регистрации γ-квантов энергии E
γ i
кристаллом
стильбена толщиной t;
Σ
t
(E
γ
i
) — полный линейный коэффициент ослабления γ-квантов в стильбене;
L(E
γ
j
,E
γ
i
) — элемент корректирующей числовой матрицы;
п — ранг матрицы.
Элементы треугольной поправочной матрицы были получены из интерполяционных
и экстраполяционных данных, выполненных на основе указанных выше
моноэнергетических источников γ-излучения. Ранг матрицы 49 - го порядка с шагом
примерно равным энергетическому разрешению спектрометра. Матрица приведена в
приложении 3. Следует отметить, что элементы матрицы в
области энергий
Е
>
7,5
МэВ получены методом экстраполяции с последующим корректированием по
проверочному спектру захватного γ-излучения азота.
Для проверки правильности результатов, полученных с помощью описанного
метода обработки, измерили энергетическое распределение γ-квантов калибровочных
Со
60
, Ро — Be и Pu — Ве источников. Экспериментально определенные значения
абсолютных активностей этих источников с точностью ±10÷15% согласуются с
паспортными данными. Количественные соотношения между нейтронами и γ-
квантами Ро — Be и Pu — Ве источников взяты из работы [30].
70
