Кухтевич В.И, Трыков Л.А., Трыков О.А. Однокристальный сцинтилляционный спектрометр (с органическим фосфором)
Подождите немного. Документ загружается.

41
n
E
E
A
⋅
=
36.2
σ
. (2.4)
Здесь En —энергия, МэВ, а постоянная А может принимать значения от 10 до 20, в
зависимости от типа (твердый или жидкий) и качества сцинтиллятора и от
геометрических условий эксперимента (полинаправленный или мононаправленный
случай).
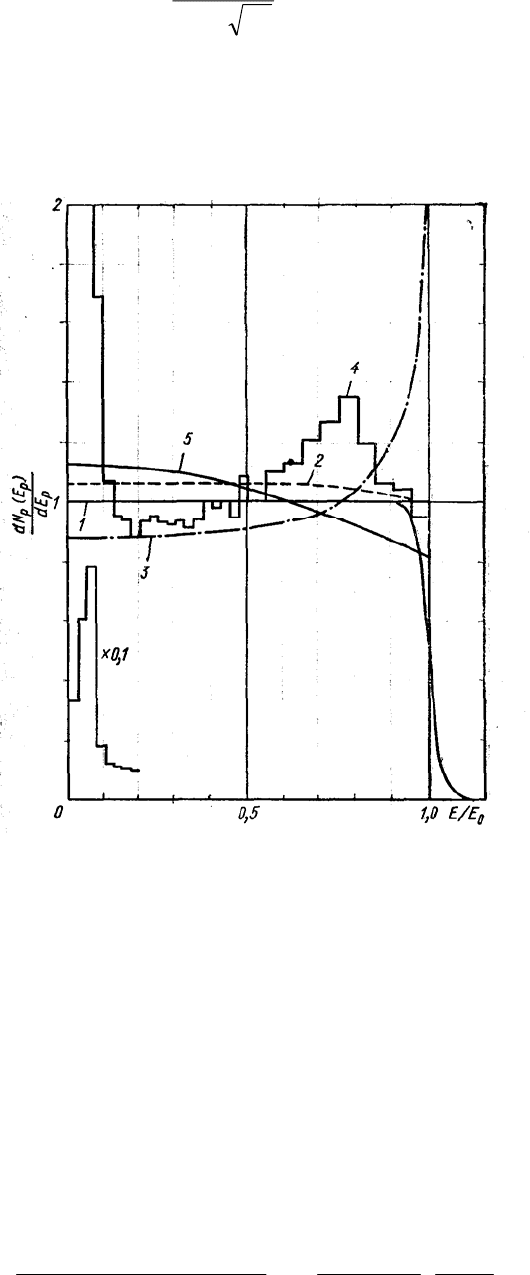
Рис. 2.1. Энергетический спектр протонов отдачи от источника
моноэнергетических нейтронов:
1 - учтено однократное рассеяние на водороде; 2 - учтено рассеяние на углероде; 3 - учтено
двукратное рассеяние на водороде; 4 - реальная форма распределения; 5 -учтена утечка
протонов через торец кристалла
.
Точно такой же функцией (2.3) описывается распределение импульсов от протонов
отдачи определенной энергии Е
р
. При этом интеграл по энергии функции (2.3) будет
характеризовать число протонов данной энергии Е
р
в энергетическом интервале,
определяемом энергетическим разрешением спектрометра ∆
Е . Исходя из
равновероятного распределения по энергии протонов отдачи, можно записать, что
полное число падающих нейтронов энергии E
n
, равно
,
)(
)(
)(
]/)([
)(
2
2
2
2
dE
E
E
dE
ENd
E
dEdEENdE
EN
E
n
n
p
pp
n
E
pppn
n
∫
∫
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅==
εε
(2.5)
41

42
где ε(E
n
) - эффективность сцинтиллятора к нейтронам энергии Е
n
. В формуле (2.5)
подынтегральное выражение в квадратных скобках есть определяемое нами
энергетическое распределение нейтронов (спектр нейтронов)
n
n
dE
EdN )(
[нейтрон/(см
2
⋅сек⋅МэВ)].
Таким образом,
)(
)(
)(
2
2
n
n
p
pp
n
n
E
E
dE
ENd
dE
EdN
ε
⋅= (2.6)
Как видно из (2.6), для того чтобы получить спектр нейтронов, достаточно
продифференцировать функцию, характеризующую энергетическое распределение
протонов отдачи dN
p
(E
p
)/dE
p
(рис. 2.2). Однако практически наблюдаемый спектр
импульсов протонов отдачи не такой «идеально» простой, как показано на рис. 2.1.
Одна из основных причин, влияющих на форму аппаратурного распределения, - это
нелинейность световыхода сцинтиллятора [1—4].
Если изменение световыхода с энергией записать в виде dP/dE
p
(рис. 2.3), где Р —
амплитуда импульсов протонов отдачи в шкале энергий, то
p
p
p
pp
dE
dP
dP
PdN
dE
EdN
⋅=
)()(
(2.7)
Тогда, подставляя (2.7) в (2.6), имеем
)(
)(
)(
n
n
p
pp
n
n
E
E
dE
dP
dP
EdN
dE
d
dE
EdN
ε
⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅⋅=
(2.8)
На рис. 2.3 в качестве примера показана связь между dN
p
(E
p
)/dE
p
и dNp(P)/dP, когда
энергия падающих нейтронов En = 15 МэВ.
42
43
Рис. 2.2. Вычисленные значения функций Nр(P)dP/dE (а) и энергетических спектров Ф(Е), полученные
из экспериментально измеренных амплитудных распределений E
n
= 0,5; 1,0; 1,5; 3,9; 5,4; 6,5 и 17,2 МэВ.
Кристалл стильбена h = 20, ∅ = 30 мм. Поток нейтронов падал перпендикулярно к оси кристалла
стильбена.
Кроме нелинейности световыхода на форму аппаратурного распределения влияют
краевые эффекты. Для того чтобы уменьшить влияние краевых эффектов, применяют
большие кристаллы.
Однако при этом существенное значение имеет многократное рассеяние на ядрах
водорода. Импульсы, возникающие в результате многократного рассеяния, сливаются в
один и с учетом нелинейности световыхода образуют спектр (рис. 2.1, кривая 4).
В органических
сцинтилляторах, содержащих водород и углерод (например,
кристалл стильбена C
14
H
12
), возможно рассеяние и на ядрах углерода. Возникающие
при этом ядра отдачи углерода образуют импульсы весьма малых амплитуд (см. рис.
2.1), и вклад их в общее распределение следует учитывать, как правило, ниже
300 ÷ 400 кэВ. Энергетический спектр импульсов от протонов отдачи, образующихся
при взаимодействии с ядрами водорода нейтронов, претерпевших однократное
рассеяние
на ядрах углерода, имеет вид столика, начинающегося в нуле и
кончающегося примерно при 0,72⋅E
n
(см. рис. 2.1).
Для небольших сцинтилляторов в определенном интервале энергий указанные
эффекты могут компенсировать друг друга, так как рассеяние на углероде увеличивает
относительный вклад импульсов с малой амплитудой, а многократное рассеяние на
водороде приводит к обратному эффекту. Из вышеизложенного следует, что возможны
заметные отклонения действительного распределения импульсов протонов отдачи от
изображенного
на рис. 2.1 (кривая 1) функцией dN
p
(E
p
)/dE
p
. (о факторах, искажающих
идеализированную форму спектра протонов отдачи более подробно см. в 2.2).
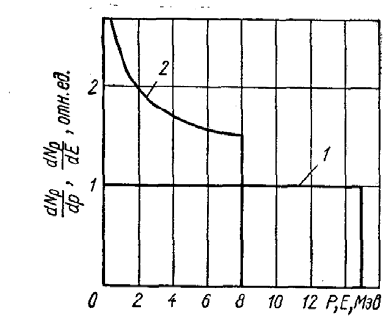
Рис. 2.3. Зависимость искажения спектра протонов отдачи (кривая 1) в стильбене, обусловленная
нелинейностью световыхода от энергии нейтронов (кривая 2).
Следовательно, преобразование аппаратурного спектра импульсов в энергетический
спектр нейтронов в общем случае следует искать не в виде (2.6) или даже (2.8), а в виде
решения следующего интегрального уравнения:
43

44
∫
Φ=
E
nnp
dEPEKEPN ,),()()(
(2.9)
где К(Е
n
,Р) — вероятность образования импульса с амплитудой в интервале
P
÷
(P+dP) нейтроном с энергией Е
n
; N
p
(Р) и Ф (Е
n
) — измеренное амплитудное
распределение и искомый энергетический спектр нейтронов соответственно.
Применительно к (2.8) и (2.9) N
p
(Р) и Ф (Е
n
) — соответственно:
.
)(
,
)(
n
n
p
dE
EdN
dP
PdN
Решить уравнение (2.9) при известных ядрах К(Е
n
, Р) N
p
(Р) можно, используя
алгоритмы матричной регуляризации [2, 5], как это и сделано в работе [2]. Однако при
этом приходится ограничиваться порядком матрицы 20 - 30, что влияет на полноту, а
следовательно, и точность получаемых энергетических распределений. Поэтому
матричная обработка, как правило, применяется только в тех случаях, когда имеются
нерегулярности в аппаратурных распределениях.
В остальных случаях, как показано в
расчетных [2,5] и экспериментальный [3,6,7] работах, с достаточно хорошим
приближением (в определенном интервале размеров кристаллов и энергий нейтронов)
ядро К(Е
n
,Р) можно представить прямоугольным столиком, если внесена поправка на
нелинейность светового выхода Р(Е), т. е. в виде
⎪
⎩
⎪
⎨
⎧
>
<
=
n
n
n
n
EPпри
EPпри
E
PEK
,0
,
),(
ε
(2.10)
При этом решение уравнения (2.10) имеет вид
.
)(
)(
)(
)()(
n
n
p
n
n
p
E
E
dE
dP
PN
dE
d
E
E
dE
dP
dE
dP
PN
dP
d
En
εε
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅−=⋅⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅−=Φ
(2.11)
Если учесть, что N
p
(Р)
→
dN
p
(E
p
)/dE
p
, Ф(Е
n
)
→
dN(E
n
)/dE
n
, то (2.11) полностью
совпадает с выражением (2.8).
В работах [2,5,8—10] подробно вычислены методом Монте-Карло формы линии
различных энергий нейтронов для кристалла стильбена с учетом многократного
рассеяния на водороде, взаимодействия с ядрами углерода и краевых эффектов. При
этом показано, что систематические ошибки, возникающие при использовании
выражения (2.8), зависят от формы нейтронного спектра. В случае
непрерывных,
медленно меняющихся энергетических распределений, т. е. распределении, в которых
скорость изменения
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅
dE
dP
dE
EdN
p
pp
)(
не менее 1,05 в рассматриваемом энергетическом
интервале dE (см. приложение 4), для кристаллов стильбена высотой 20 ÷ 40 мм и
диаметром 30 мм ошибки составляют несколько процентов (5—3%) в энергетическом
диапазоне от 0,3 до 14 ÷ 15 МэВ. Для решения многих задач спектрометрии этого
вполне достаточно.
Для получения энергетических распределений нейтронов с помощью выражения
(2.8) необходимо знать эффективность
сцинтиллятора ε(E
n
), которую удобно
44

45
определять как отношение числа протонов отдачи к числу падающих нейтронов.
Эффективность сцинтиллятора, содержащего водород и углерод,
легко рассчитать в
предположении, что происходят только однократные взаимодействия между
падающими нейтронами и ядрами сцинтиллятора. Число протонов отдачи,
образованных в кристалле высотою h, на который падает поток нейтронов N с энергией
Е
n
, равно
[
]
h
CH
H
np
CH
eNhEN
⋅Σ+Σ−
−⋅
Σ+Σ
Σ
⋅=
)(
1
1),(
(2.12)
где Σ
H
и Σ
C
— макроскопические сечения рассеяния нейтронов энергии Е
п
на ядрах
водорода (табл. 2.1) и углерода соответственно. Тогда эффективность в приближении
однократного рассеяния равна
[
h
CH
H
np
n
CH
e
N
hEN
hE
⋅Σ+Σ−
−⋅
Σ+Σ
Σ
==
)(
1
1
1
),(
),(
ε
]
(2.13)
Выражение (2.13) получено в предположении, что ядра углерода в сцинтилляторе в
результате взаимодействия уменьшают первоначальный поток нейтронов. В
действительности, из-за того что полное сечение углерода практически обязано
упругому рассеянию в большом интервале энергий, правильнее считать, что первичный
поток нейтронов не убывает при взаимодействии с ядрами углерода. При этом, как
показывают
расчеты [1,5], эффективная длина пробега нейтронов и начальная энергия
E
n
(средняя энергия упруго рассеянных на углероде нейтронов равна примерно 0,85⋅Е
n
)
не значительно искажаются рассеянием на углероде. Таким образом, в первом
приближении можно считать, что ядра углерода не вносят искажений в процессы
взаимодействия нейтронов с ядрами сцинтиллятора, т.е. взаимодействие происходит
только как бы с ядрами водорода. В таком случае эффективность вместо (2.13) запишем
в виде
h
n
H
ehE
⋅Σ−
−= 1),(
ε
(2.13)
Действительно, во многих случаях эффективность рассматриваемых сцинтилляторов
очень хорошо описывается выражением (2.14) [1,2,5].
Часто задают вопрос: почему при преобразовании амплитудных распределений в
энергетические при помощи (2.9), (2.11) в качестве эффективности не применяется
выражение вида
()
?11),(
h
n
i
ni
H
e
E
B
EB
⋅Σ−
−⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
ε
Таблица 2.1
Зависимость Σ
H
=
n
H
⋅σ
H
для стильбена от энергии нейтронов*
Е, МэВ
n
H
⋅σ
H
, см
-1
Е, МэВ
n
H
⋅σ
H
, см
-1
0,1 0,5973 19 0,0239
0,2 0,4530 20 0,0227
45

46
0,4 0,3231 21 0,0213
0,6 0,2613 22 0,0203
0,8 0,2242 23 0,0193
1,0 0,1989 24 0,0184
2,0 0,1.356 26 0,0160
3 0,1064 28 0,0156
4 0,0884 30 0,0144
5 0,0758 34 0,0125
6 0,0664 38 0,0111
7 0,0589 42 0,0099
8 0,0530 46 0,00882
10 0,0439 50 0,00798
12 0,0374 54 0,00728
16 0,0303 60 0,00635
• При составлении таблицы использовали следующие данные [1]: молекулярный вес 180,24;
плотность 1,164 г
⋅
см
-3
; п
H
= 0,0467⋅10
24
атом
⋅
см
-3
;
п
C
= 0,545⋅10
24
атом
⋅
см
-3
. Абсолютная точность для n
H
⋅σ
H
составляет 1%
Дело в том, что возможны две записи интегрального уравнения (2.9) (B
I
-
энергетический порог спектрометра или порог, задаваемый шагом матрицы):
∫
Φ=
E
nnp
dEPEKEPN ,),()()(
(2.15)
и
∫
Φ=
max
min
),()()(
E
E
innip
dEBEEBN
ε
(2.9)
Уравнения (2.15) и (2.16) принципиально отличаются друг от друга. Ядром
интегрального уравнения (2.15) является форма линии спектрометра К(Е
п
,Р), а
уравнения (2.16) — счетная эффективность регистрации счетчика ε(E
n
,В
i
). При
решении (2.15) в виде (2.11) или (2.8), т. е. в предположении прямоугольного
распределения аппаратурного спектра монолинии, не имеет значения, какая часть
столика (см. рис. 2.1) окажется под порогом спектрометра. Важно, чтобы под порогом
46

47
не оказалась та его часть, где производная
2
2
)(
p
pp
dE
ENd
не равна нулю. После этого,
умножив результат дифференцирования на E
n
, получим с учетом эффективности ε(E
n
)
полную информацию о числе падающих на детектор нейтронов. При этом
действительная эффективность спектрометра в Е
n
раз меньше эффективности,
определяемой величиной
, и это существенно влияет на
статистическую точность результатов измерений.
h
n
H
ehE
⋅Σ−
−= 1),(
ε
В работах [2,8,11] была сделана попытка выполнить преобразование аппаратурных
распределений в энергетические решением интегрального уравнения (2.16). Этот метод
был назван методом счетных эффективностей, так как ядром уравнения (2.16) является
счетная эффективность
(
h
n
i
ni
H
e
E
B
EB
⋅Σ−
−⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= 11),(
ε
)
. Предполагалось, что при
использовании ядра вида ε(E
n
,В
i
) можно заметно повысить точность получаемых
энергетических распределений, так как эффективность этого метода имеет лучшее
приближение к полной эффективности спектрометра:
. При этом
уравнение (2.16) представлялось приближенно в виде системы линейных уравнений
h
n
H
ehE
⋅Σ−
−= 1),(
ε
ik
n
k
kpi
AN
∑
=
Φ=
1
(2.17)
которая разрешается относительно Ф
k
. Матричные элементы A
ik
включают счетные
эффективности ε(E
n
,В
i
), а шаг матрицы определяется разностью B
i+1
- B
i
.
О недостатках матричной обработки уже упоминалось, однако развитие методов
обработки (включая и матричные), позволяющих использовать полную эффективность
спектрометра, несомненно, заслуживает большего внимания.
В заключение отметим некоторую особенность преобразования амплитудных
распределений в энергетические спектры с помощью (2.8) при определении
абсолютных потоков нейтронов.
Во время измерений аппаратурных распределений имеют дело с амплитудами
импульсов,
выраженных не в энергетических единицах, а в вольтах или в числе
каналов анализатора, т. е. в единицах шкал измерительных приборов. Поэтому
необходимо выполнять нормировку, обеспечивающую связь между шкалой
измерительных приборов и энергетической шкалой. Такую нормировку выполняют с
помощью калибровочных γ-источников.
Обозначим амплитуду импульсов, выраженную, например, в каналах анализатора,
V. Пусть
при этом P=CV, где С— нормировочная константа. Тогда выражение N(V)
=CN
p
(P) будет отражать связь амплитудного распределения N(V) с аппаратурным
распределением N
р
(P). При этом формулы (2.8) или (2.11), по которым осуществляется
преобразование аппаратурных распределений в энергетические, примут вид
ε
n
n
E
dE
dP
VN
dE
d
CE ⋅
⎥
⎦
⎤
⎢
⎣
⎡
=Φ )()(
(2.18)
Нормировочную константу С можно определить следующим образом. Обозначим
47

48
но
о
к
, а л
мер канала анализатора X, который соответствует максимальной энергии
комптоновских электронов тдачи Е
э
макс
калибровочного γ-источника. Далее,
обозначим величину световыхода Р(Е) в мегаэлектронвольтах, оторый определяется
на электростатических генераторах или по методу известных сечений (см. § 2.2),
соответствующего этой энергии Е
э
макс
, через Р
X
. Тогда амплитудное значение
световыхода V(E}, выраженное, например в числе каналов нализатора, д я любой
энергии протонов отдачи в зависимости от Р(Е) будет иметь вид
.
)(
)(
)(
EP
XEP
EV
X
=
(2.19)
Отсюда C=X/P
X
(E) и выражение (2.18) примет вид
.
1
)()(
h
n
X
n
H
e
E
dE
dP
VN
dE
d
P
X
E
Σ−
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅⋅=Φ
(2.20)
В формулах (2.18)—(2.20) при дифференцировании разностным способом
исп ь
С
ол зуется фиксированный энергетический интервал ∆E
n
. помощью выражения
(2.18) легко получить запись формулы для поканального дифференцирования или для
дифференцирования по интервалу, кратному некоторому числу каналов п. Для этого
обозначим выражение, записанное в уравнении (2.18) в квадратных скобках, F(V),
тогда
h
n
h
n
h
n
H
HH
e
E
dE
dP
dE
dP
VN
dV
d
C
e
E
dE
dV
VF
dV
d
C
e
E
VF
dE
d
CE
Σ−
Σ−Σ−
−
⋅⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
=
−
⋅=
−
=Φ
1
)(
1
)(
1
)()(
2
, (2.21)
Выражение (2.21) и является записью для поканального дифференцирования.
§2.2. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ФОРМУ ЛИНИИ
Нелинейность световыхода органических сцинтилляторов
ре и о
СПЕКТРОМЕТРА
Как уже отмечалось, в сцинтилляционном спектрометре непосредственно
гистр руем й количественной величиной является спектр амплитуд импульсов,
появляющихся на выходе ФЭУ. При соответствующих условиях этот импульс линейно
связан со световой вспышкой кристалла. Однако световспышка в кристалле не связана
линейно с энергией, переданной протоном кристаллу. Связь световыхода с энергией
для различных заряженных частиц в первом
приближении (см. приложение 2) можно
представить полуэмпирической формулой Биркса [1]:
48
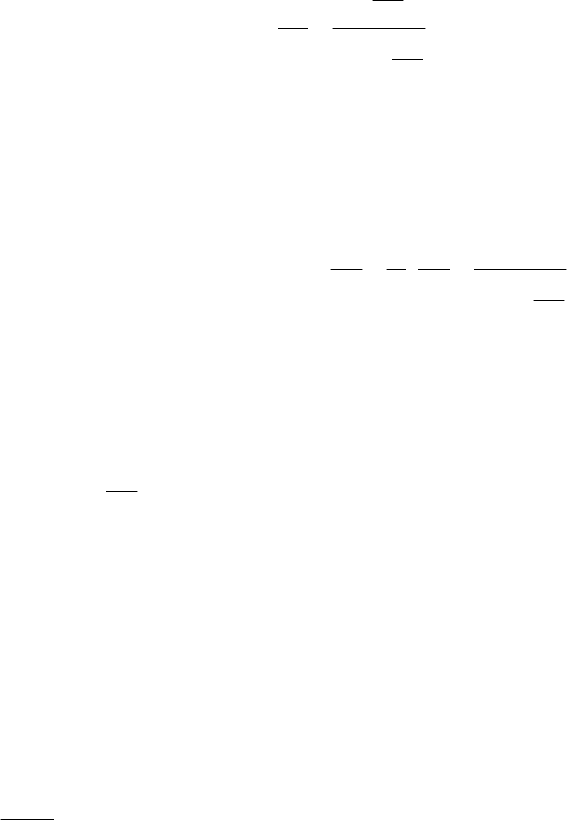
49
dx
dE
kB
dx
dE
A
dx
dS
+
=
1
, (2.22)
где S—световыход кристалла; х—длина пробега частицы в кристалле; Е—энергия
частицы; A и kB—постоянные, определяемые экспериментально.
Равенство (2.22) удобно представить в виде
,
1
11
dx
dE
kB
dE
dS
AdE
dP
+
=⋅=
(2.23)
где P=S/A. Величина dE/dx для электронов мала, поэтому значением kB dE/dx можно
пренебречь и dP/dE
≅
1. Тогда P=E
э
, где Е
э
— энергия электронов.
Для протонов с энергией Е
р
< 50 МэВ величиной dE/dx пренебрегать нельзя. В этом
случае, зная kB и
)(
p
E
dx
dE
можно определить (рассчитать) dP/dE, численно интегрируя
(2.23).
Такие расчеты были проведены для кристалла стильбена. Значения dE/dx
рассчитывают по таблицам, приведенным в работах [1,12] .Результаты расчетов
представлены в табл. 2.2 для kB= 0,0120 мг/(см
2
⋅
кэВ).
Исследованию световыхода посвящено много теоретических и экспериментальных
работ [13—17]. Большинство данных, полученных разными авторами, несколько
отличаясь по абсолютному значению, дают довольно хорошо совпадающий по форме
относительный ход функции Р(Е). Эти результаты Р(Е) можно представить как
i
i
C
EP
EP
)(
)( =
, где С
i
- постоянный коэффициент, определяющий абсолютную
нормировку функции Р(Е) для данного автора. Так, например, световыход, полученный
в работе [14], отличается от данных работы [27] на коэффициент С ≈ 1,38, а в работе
[16]—на коэффициент С ≈ 1,1. Наблюдаемые различия в значениях функции Р(Е)
можно объяснить тем, что на величину световыхода влияют ориентация стильбенового
кристалла
относительно падающего пучка нейтронов [1,18], качество самого кристалла,
тип фотоумножителя и линейность вторичной электронной аппаратуры
(предусилителя, эмиттерного или катодного повторителя, основного усилителя,
анализатора импульсов). Таким образом, следует иметь в виду не световыход
сцинтиллятора отдельно, а световыход всего спектрометра в целом.
Следовательно, недостаточно один раз с высокой точностью определить световыход
спектрометра. Для
получения энергетических распределений с наименьшими
ошибками необходимо проводить контроль и корректировку световыхода
непосредственно в процессе измерений. При проведении экспериментальных работ на
источниках моноэнергетических нейтронов такой контроль осуществить нетрудно.
Обычно световыход определяют с помощью электростатических генераторов —
источников моноэнергетических нейтронов. При этом ошибки в величине световыхода
зависят от точности градуировки энергетической шкалы
и от точности задания энергии
49
50
регистрируемых нейтронов [в реакциях Т(р, п)Hе
3
, D(d, п)Не
3
и т. д.]. Как правило,
суммарная ошибка этих факторов составляет не более 1—1,5%.
При работе с источниками немоноэнергетических нейтронов контроль и
корректировку зависимости Р(Е) можно осуществить методом «известных сечений».
Для этого в условиях хорошей геометрии измеряют аппаратурные распределения
нейтронов за образцами из элементов, сечения которых имеют резко выраженную
резонансную структуру
, известную с точностью ~1 % по энергии. Если величина
пропускания Т ≤ 10
-1
, в аппаратурных распределениях проявляются четкие
нерегулярности, отражающие соответствующую резонансную структуру в сечениях. В
качестве эталонов могут применяться образцы, например, из графита и бериллия для
Е>
0,5
÷
2
МэВ и из железа и бериллия для Е
<
1
÷
0,5 МэВ.
На рис. 2.4 показаны амплитудные распределения импульсов нейтронов для
образцов из углерода толщиною l
= 40 см. и из железа толщиною l
= 22 см. Области,
отмеченные стрелками, соответствуют аппаратурным распределениям протонов
отдачи, как если бы они были получены от почти монохроматических нейтронов
соответствующих энергий.
50
