Козлов В.В. Надёжность горных машин и оборудования

Подождите немного. Документ загружается.

ции.

К о р р е л я ц и о н н ы й м о м е н т (или момент свя-

зи) двух случайных величин Х и Y - это математическое ожида-

ние произведения центрированных случайных величин

для дискретных

∑

−−=

i j

ijyjxixy

PmymxK ))((

для непрерывных

∫∫

∞

∞−

∞

∞−

−−= dydxyxfmymxK

yxxy

),())((

где m

, m

- математические ожидания величин Х и Y;

- вероятность отдельных значений x

и y

Корреляционный момент одновременно характеризует

связь между случайными величинами и их рассеяние. По своей

размерности он соответствует дисперсии для независимой слу-

чайной величины.

Если случайные величины независимы, то корреляцион-

ный момент равен нулю, так как его можно представить как про-

изведение центральных моментов величин Х и Y, которые равны

нулю.

Поэтому для выделения характеристики связи между слу-

чайными величинами переходят к коэффициенту корреляции

=ρ

Если хотя бы одна из случайных величин имеет малое

рассеяние, то корреляционный момент мал даже при тес-

ной зависимости между случайными величинами.

где

SиS - средние квадратические отклонения случайных

величин.

Значения р = 1 и р = -1 свидетельствуют о функциональной

зависимости, значение р = 0 свидетельствует о некоррелирован-

ности случайных величин. Для независимых случайных величин

также р = 0.

Рассматривают корреляцию как между величинами, так и

между событиями, а также множественную корреляцию, характе-

ризующую связь между многими величинами и событиями.

При более подробном анализе вероятностной связи опре-

деляют условные математические ожидания случайных величин

и m

x/y

т. е. математические ожидания случайных величин Y и Х

при заданных конкретных значениях Х и У соответственно.

Для нормально распределенных величин Y и Х уравнение

регрессии

Y по Х имеет вид

)(

/ x

yxy

pmm −+=

;

К о э ф ф и ц и е н т к о р р е л я ц и и характеризует

степень тесноты зависимости и может изменяться в преде-

лах -1≤ р ≤ 1 .

Зависимость условного математического ожидания

my/x от х называют регрессией Y по X. Зависимость mx/y

от у соответствует регрессии Х поY.

для регрессии X по Y

)(

/ y

xyx

pmm −+=

где р - коэффициент корреляции;

yxyx

SSиmm ,, математические ожидания и, среднеквадра-

тические отклонения случайных величин Х и Y соответственно.

Результаты наблюдения случайных величин Y и Х пред-

ставляют парными значениями y

, x

i-го наблюдения, где i = l, 2,

. . ., n; n - число наблюдений.

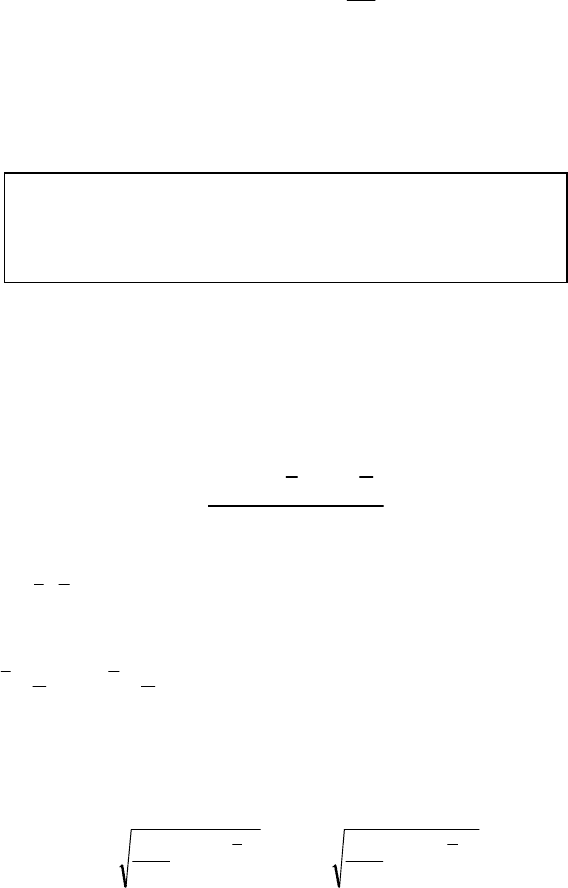
Оценку r коэффициента корреляции р определяют по

формуле

ssn

yyxx

)1(

))((

−

−−

∑

где yx, - оценки математических ожиданий

mиm соответ-

ственно, т. е. средние из n наблюдений значений

∑ ∑

== ;

;

ss , - оценки среднеквадратических отклонений S

и S

соответственно:

.)(

;)(

∑∑

−

=−

−

= yy

sxx

iyix

Важнейшей областью применения корреляционно-

го анализа к задачам надежности является обработка и

обобщение результатов эксплуатационных наблюдений.

Обозначив оценку условных математических ожиданий

yxxy

, соответственно через

∧∧

XиY , уравнения эмпири-

ческой регрессии Y по Х и Х по Y записывают в следующем ви-

де:

).(

);(

rxX

ryY

−+=

∧

Как правило, практическую ценность имеет лишь одна из

регрессии.

Отметим, что при коэффициенте корреляции г=1 уравне-

ния регрессий тождественны.

5.3 Регрессионный анализ, метод наименьших

квадратов

Основной характеристикой вероятностной связи между

случайной величиной Y и неслучайной х является регрессия, т. е.

зависимость математического ожидания (среднего значения) m

случайной величины Y от х. График этой зависимости называется

линией регрессии.

При анализе предполагают, что точно или приближенно

соблюдаются следующие предпосылки:

Регрессионный анализ - нахождение зависимости

my от x по отдельным значениям величин, обычно по экс-

периментальным точкам.

а) результаты измерений

yyy ...,

, где n - число изме-

рений, представляют собой выборку объемом n из нормально

распределенной генеральной совокупности значений Y;

б) дисперсия случайной величины Y для любого значения

независимой переменной х является постоянной;

в) независимая переменная имеет малую ошибку по срав-

нению с ошибками результатов наблюдений;

г) вид функциональной зависимости среднего значения

случайной величины

m от х предварительно постулируют на

основе каких-либо теоретических или практических зависимо-

стей или выбирают в виде полинома.

Оценка параметров линейной регрессионной

зависимости по методу наименьших квадратов

Линейная зависимость между величинами пли их лога-

рифмами является наиболее распространенной. Уравнение линии

регрессии записывают в виде

0 xy

m ββ +=

где

, ββ - параметры или коэффициенты регрессии.

Оценкой линии регрессии является эмпирическая линия

регрессии, уравнение которой имеет вид

bxbY +=

∧

где

,, bbY

∧

- оценки величин

,, ββ

m соответственно.

Коэффициенты регрессии b и b

находим методом наи-

меньших квадратов, в основе которого положено требование

минимизации квадратов отклонений реализации (результатов

измерений) случайной величины от линии регрессии:













−=

∑

∧

)(min Yyu

или после подстановки

∧

{

}

,)(min

∑

−−=

bxbyu

где у

- реализация случайной величины в i-м опыте;

- значение независимой переменной в i-м опыте;

n - число опытов.

Известно, что минимум некоторой функции наступает при

равенстве нулю частных производных по всем неизвестным:

∑

=−−−=

∂

0)(2

bxby

;

∑

=−−−=

∂

0)(2

0 iii

xbxby

Раскрывая скобки, проводим суммирование и после не-

сложных преобразований получаем систему нормальных уравне-

ний

∑ ∑ ∑ ∑ ∑

=+=+ .;

00 iiiiii

xyxbxbyxbnb

Из решения системы получаем формулы для коэффициен-

тов b и b

∑ ∑

∑

−=

−

= ).(

;

)(

iiii

xby

xxn

yxyxn

Нелинейная регрессия В простейшей форуме описывается

квадратическим уравнением

210

xxm

βββ ++=

Соответственно уравнение эмпирической кривой регрес-

сии имеет вид

210

xbxbbY ++=

∧

По аналогии с линейной регрессией методом наименьших

квадратов составляем нормальные уравнения:

∑ ∑ ∑

=++ ;

210 iii

yxbxbnb

∑ ∑ ∑∑

=++ ;

10 iiiii

yxxbxbxb

∑ ∑ ∑∑

=++ .

10 iiiii

yxxbxbxb

Решая систему нормальных уравнении, определяем коэф-

фициенты регрессии b

, b

и b

В изложенной выше форме регрессионный анализ приме-

няют для обработки результатов пассивного эксперимента, т. е.

эксперимента, в котором невозможно назначать и поддерживать

на выбранном уровне значения неслучайной величины.

Более эффективным является активный эксперимент, по-

зволяющий применять математическое планирование экспери-

мента и тем самым уменьшать время и число опытов.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Напишите формулу плотности распределения (в общем

виде) случайной функции зависящей от одного аргумента.

2. Как определяются m

и S

случайной функции зави-

сящей от нескольких аргументов?

3. Каков физический смысл коэффициента корреляции?

4. Запишите формулу коэффициента корреляции и пояс-

ните его составляющие.

5. Что показывает уравнение регрессии?

ГЛАВА 6

СЛУЧАЙНЫЕ ФУНКЦИИ

6.1 Определение случайной функции [5]

Случайной функцией X(t) называется функция, которая в

результате опыта может принять тот или иной неизвестный зара-

нее конкретный вид.

По аналогии с реализацией случайной величины X=x

ча-

стную конкретную случайную функцию x

(t), полученную в ре-

зультате опыта, называют реализацией случайной функции X(t).

Если произвести несколько опытов, то получим n реализа-

ций x

(t) случайной функции X(t).

Для практических расчетов пользуются числовыми харак-

теристиками случайной функции, основными из которых являют-

ся: математическое ожидание, дисперсия и корреляционная

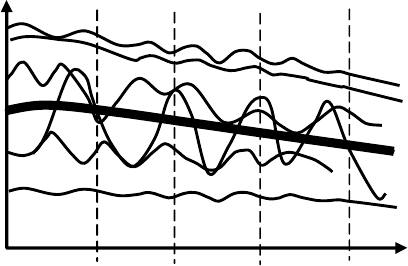
функция/ Рис 6.1

Рисунок 6.1 - Осциллограммы случайного процесса

X(t)

(t)

m(t

) m(t

)

m(t

)

m(t

)

Пусть имеет некоторое семейство n реализаций x

(t) слу-

чайной функции X(t).

Зададимся какими-либо фиксированными значениями па-

раметра t: t=t

; t=t

и произведем в этих точках “сечения”

всех реализаций случайной функции. Очевидно, в каждом “сече-

нии” n реализаций случайной функции превратятся в n значе-

ний, т.е. в сечении t=t

величины x

), x

), ..., x

будут представлять собой n значений случайной величины X(t),

имеющей функцию плотности распределения f[x(t

)]; в сечении

t=t

величины x

); x

), ..., x

) ..., x

) дают n значений

случайной величины X

), имеющей плотность распределения

f[x(t

)] и т.д.

Таким образом, для каждого сечения t

семейства X(t), та-

ким образом, определена частная плотность вероятности (распре-

деления) обычной случайной величины f[x(t

)], для которой опре-

деляют математическое ожидание

∫

∞

∞−

== dxxxftmtxМ

)()()]([

, (6.1)

и дисперсию

∫

∞

∞−

⋅−== dxxfmxttxD

xii

)()()()]([

(6.2)

Если далее определить подобным образом функции m(t

) и

) для достаточно близких значений t

(через малые интервалы

∆t), а затем соединить все точки m(t

) и σ

) плавной кривой, то

получим соответственно функцию (жирная кривая рис.6.1)

∫

∞

)()]([)()()]([ tdxtxftxtmtxМ

, (6.3)