Козлов В.В. Надёжность горных машин и оборудования
Подождите немного. Документ загружается.


51
Иногда удобнее оперировать с дисперсией D=S
2
.
Математическое ожидание определяет на
графике (см. рис. 4.4) положение петли, а сред-
нее квадратнческое отклонение — ширину
петли.
Кривая плотности распределения тем острее и
выше, чем меньше S. Она начинается от t=-∞ и рас-
пространяется до t=+∞ . Это не является существен-
ным недостатком, особенно если m
t
≥3S, так как пло-
щадь, очерченная уходящими в бесконечность ветвя-
ми кривой плотности, выражающая соответст-
вующую вероятность отказов, очень мала. Так, веро-
ятность отказа за период времени до (m
t
—3S) состав-
ляет всего 0,135% и обычно не учитывается в расче-
тах. Вероятность отказа до( m
t
—2S) равна 2,175%.
Наибольшая ордината кривой плотности распределе-
ния равна 0,399/S.

52
Рисунок 4.5.- Основные характеристики нормального рас-
пределения при разных значениях среднего
квадратического отклонения: а – плотность
вероятности f(t); б – вероятность безотказ-
ной работы P(t); в – интенсивность отказов
λ(t).
Интегральная функция распределения:
dttftF
t
∫
∞
=
_
)()(
Вероятность отказа и вероятность безотказной работы со-
ответственно Q(t)=F(t); P(t)=1- F(t).
53
Вычисление интегралов заменяют использованием таблиц.
Таблицы для нормального распределения в функции (t-m
t
) и S
были бы громоздкими, так как имели бы два независимых пара-
метра. Можно обойтись небольшими таблицами для нормального
распределения, у которого m
x
=0 и S
x
=1.Центрированная СВ.
Для этого распределения функция плотности
2
0
2
2
1
)(
x
exf
−
=
π
имеет одну переменную x. Величина x является центриро-
ванной, так как m
x
=0 и нормированной, так как S
x
=1 Функция
плотности распределения записывается в относительных коорди-
натах с началом на оси симметрии петли.
Функция распределения есть интеграл от плот-
ности распределения F
0
(х)=
∫
∞−
x
o
dxxf )(
Из этого уравнения следует, что F
x
(x)+F
0
(-x)=1, отсюда
F
x
(-x)=1-F
x
(x)
Для использования таблиц следует применять подстановку
х=( t—m
x
)/S; при этом х называется квантилью нормированно-
го нормального распределения и обычно обозначается u
p
.
Плотность распределения и вероятность безотказной рабо-
ты соответственно f(t)-=f
0
(x)/S; Q(t)=F
0
(x); P(t)=l-F
0
(x), где f
0
(x)
F
0
(x) берут по таблицам [3].
В табл. 4.1 приведены непосредственные значения P(t) в
зависимости от x=u
p
=(t-m
t
)/S в употребительном диапазоне

54
В литературе по надежности часто вместо интегральной
функции распределения F
0
(x) пользуются функцией Лапласа:
∫ ∫
−
==
x x
x
edxxfxФ
0 0
2
0
2
2
1
)()(
π
(4.11)
Очевидно, что
∫ ∫
∞−
+=+=
0
0
000
)(5.0)()()(
x
xФdxxfdxxfxF
Вероятность отказа и вероятность безотказной работы, вы-
раженные через функцию Лапласа, отличающиеся пределами
интегрирования, имеют вид:
−
+=
S
mt
ФtQ
t
5.0)(
;
−
−=
S
mt
ФtP
t
5.0)(
(4.12)
Сравнивая изделия с одинаковой средней наработкой до
отказа и разным средним квадратическнм отклонением S, нужно
подчеркнуть, что хотя при больших S и имеются экземпляры с
большой долговечностью, но чем меньше S, тем много лучше
изделия.
Помимо задачи оценки вероятности безотказной работы за
данное время или за данную наработку встречается обратная за-
дача — определение времени или наработки, соответствующих
заданной вероятности безотказной работы.
55
Значения этой наработки (времени) определяют с помо-
щью квантили нормированного нормального распределения
t=m
t
+u
0
S. (4.12а)
Значения квантилей даются в таблицах в зависимости от
требуемой вероятности, в частности от вероятности безотказной
работы (табл. 4.1).
Операции с нормальным распределением проще, чем с
другими, поэтому им часто заменяют другие распределения. При
малых коэффициентах вариации S/m
t
нормальное распределение
хорошо заменяет биномиальное, пуассоново и логарифмически
нормальное.
Распределение суммы независимых случайных вели-
чин U=X+Y+Z, называемое композицией распределений, при
нормальном распределении слагаемых также является нормаль-
ным распределением.
Математическое ожидание и дисперсия композиции соот-
ветственно равны
m
0
=m
x
+m
y
+m
z
;
2222
zyxu
SSSS ++=
где m
x
, m
y
, m
z
- математическое ожидание случайных величин
X,Y,Z;
222
,,
zyx
SSS - дисперсия тех же величин.
Пример. Оценить вероятность P(t) безотказной работы в
течение t=1.5*10
4
ч изнашиваемого подвижного сопряжения, если
ресурс по износу подчиняется нормальному распределению с
параметрами m
t
=4*10
4
ч, S=10
4
ч.

56
Решение. Находим квантиль 5.2
10
10*410*5.1
4
44
−=
−
=
p
u
по табл. 4.1, определяем, что P(t)=0.9938.
Пример. Оценить 80%-ный ресурс t
0.8
гусеницы трактора,
если известно, что долговечность гусеницы ограничивается по
износу, ресурс подчиняется нормальному распределению с пара-
метрами
m
t=10
4
ч; S=6*10
3
ч.
Решение. При P(t)=0.8; u
p
=-0.84:
t
0.8
=m
t
+u
p
S=10
4
-0.84*6*10
3
≈5*10
3
ч.
Усеченное нормальное распределение получается из
нормального при ограничении интервала изменения случайной
величины. Оно, в частности, вносит уточнение в расчеты надеж-
ности по сравнению с нормальным распределением при больших
значениях коэффициента вариации υ=S:/m
t
.
Функция плотности распределения записывается так же,
как плотность нормального распределения, но с коэффициентом
пропорциональности с:
2
2
0
2
)(
2
)(
S
tt
e
S
c
tf
−
−
=
π
, (4.13)
где t
0
- значение случайной величины, соответствующее макси-
муму f(t) и называемое модой.
Коэффициент с для распределения, ограниченного преде-
лами изменения t от а до b, определяется из условия
)()(1)( aFcFcdttf
b
a
−==
∫
,

57
где F(b) и F(a) – значение функции нормального распределения
для предельных значений t.
Отсюда
)()(
1
aFbF
c
−
=
.
Пользуясь функцией F
0
нормального распределения нор-
мированной и центрированной случайной величины, запишем:
−
−
−
=
S
ta
F
S
tb
F
c
0
0
0
0
1
Основное применение усеченное нормальное распределе-
ние имеет с параметрами, a=0 и b=∞ отражающее в задачах на-
дежности невозможность отказов при отрицательных значениях
времени. Тогда
)/
0
(
0
1
StF
с =
Значения с можно выбрать в зависимости от t
0
/S:
t
0
/S: ............ 1 2 3
с .............. 1,189 1,023 1,001
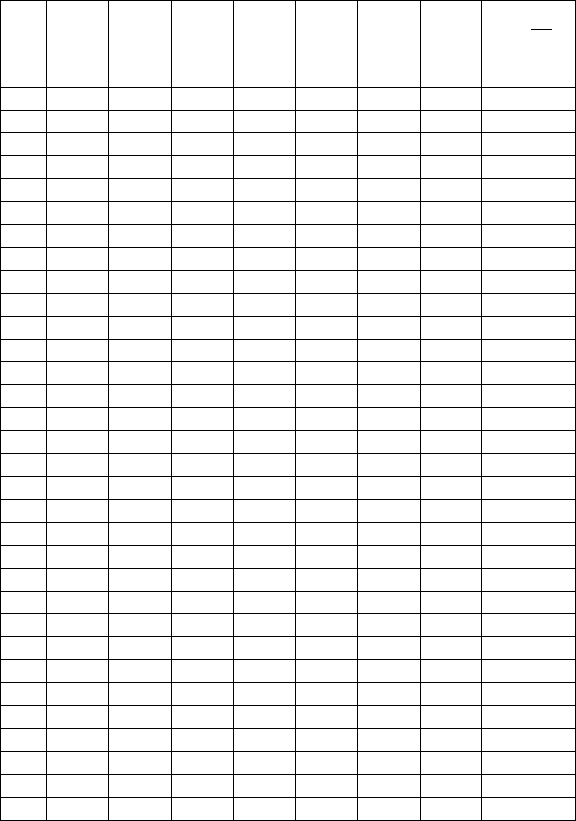
Таблица 4.1
Нормальное распределение Распределение Вейбулла
Кван-
тиль u
p
Вероят-
ность
Кван
тиль
u
p
Вероят-
ность
Пара
метр
формы m
1/m B
m
C
m
Коэффициент
вариации
58
безотказ-
ной рабо-
ты P(t)
безотказ-
ной рабо-
ты P(t)
ь
и
ь
с
=ν
1 2 3 4 5 6 7 8 9
0,000
0,5 -2,054 0,98 0,4 2,5 3,32 10,4 3,14
-0,1 0,5398 -2,1 0,9821 0,417 2,4 2,98 8,74 2,93
-0,126
0,55 -2,17 0,985 0,435 2,3 2,68 7,38 2,75
-0,2 0,5793 -2,2 0,9861 0,455 2,2 2,42 6,22 2,57
-0,253
0,6 -2,3 0,9893 0,476 2,1 2,2 5,27 2,4
-0,3 0,6179 -2,326 0,99 0,5 2,0 2,0 4,47 2,24
-0,385
0,65 -2,4 0,9918 0,526 1,9 1,83 3,81 2,08
-0,4 0,6554 -2,409 0,992 0,556 1,8 1,68 3,26 1,94
-0,5 0,6915 -2,5 0,9938 0,588 1,7 1,54 2,78 1,8
-0,524
0,7 -2,576 0,995 0,625 1,6 1,43 2,39 1,67
-0,6 0,7257 -2,6 0,9953 0,667 1,5 1,33 2,06 1,55
-0,674
0,75 -2,652 0,996 0,714 1,4 1,24 1,78 1,43
-0,7 0,758 -2,7 0,9965 0,769 1,3 1,17 1,54 1,32
-0,8 0,7881 -2,748 0,997 0,833 1,2 1,1 1,33 1,21
-0,842
0,8 -2,8 0,9974 0,909 1,1 1,05 1,15 1,1
-0,9 0,8159 -2,878 0,998 1,0 1,0 1,0 1,0 1,0
-1,0 0,8413 -2,9 0,9981 1,1 0,909 0,965 0,878 0,91
-1,036
0,85 -3 0,9986 1,2 0,833 0,941 0,787 0,837
-1,1 0,8643 -3,09 0,999 1,3 0,769 0,924 0,716 0,775
-1,2 0,8849 -3,291 0,9995 1,4 0,714 0,911 0,659 0,723
-1,282
0,9 -3,5 0,9998 1,5 0,667 0,903 0,615 0,681
-1,3 0,9032 -3,719 0,9999 1,6 0,625 0,897 0,574 0,64
-1,4 0,9192 1,7 0,588 0,892 0,54 0,605
-1,5 0,9332 1,8 0,556 0,889 0,512 0,575
-1,6 0,9452 1,9 0,526 0,887 0,485 0,547
-1,645
0,95 2,0 0,500 0,886 0,463 0,523
-1,7 0,9554 2,1 0,476 0,886 0,439 0,496
-1,751
0,96 2,2 0,455 0,886 0,425 0,48
-1,8 0,9641 2,3 0,435 0,886 0,409 0,461
-1,881
0,97 2,4 0,417 0,887 0,394 0,444
-2,0 0,9772 2,5 0,400 0,887 0,38 0,428
Примечание к таблице 4.1: 1. Под t понимается время или
другие случайные величины. 2. Для логарифмически нормально
распределения u
p
=(ln t-µ)/S.

59
Таким образом, при to>2S коэффициент с очень близок к
единице. Вероятность безотказной работы
−
=
S
tt
FctP
t
0
*)(
(4.14)
Средний ресурс
)/(*
00
StSftm
t
+
=
(4.15)
где f*—функция, которая определяется по таблице [4.1].
Примером усеченных распределений может быть распре-
деление параметра качества изделий после отбраковки части из-
делий по этому параметру.
В логарифмически нормальном распределении лога-
рифм случайной величины распределяется по нормальному зако-
ну. Как распределение положительных величин, оно несколько
точнее, чем нормальное, описывает наработку до отказа деталей,
в частности, по усталости. Его успешно применяют для описания
наработки подшипников качения и других изделий.
Логарифмически нормальное распределение удобно
для случайных величин, представляющих собой произ-
ведение значительного числа случайных исходных ве-
личин, подобно тому как нормальное распределение
удобно для суммы случайных величин.
Плотность распределения (рис. 4.6) описывается зависимо-
стью
60
2
2
2
)(ln
2
1
)(
S
t
s
St
tf
µ
π
−
−
=
(4.16)
где р и S — параметры, оцениваемые по результатам испытаний.
Так, при испытаниях N изделий до отказа
Т
дте
ш
Σ
=≈
*
µµ
2*
)(ln
1
1
µ−Σ
−
=≈
i
t
N
sS
,
где µ* и s - оценка параметров µ и S.
Вероятность безотказной работы можно определить но
таблицам для нормального распределения (см. табл. 4.1) в зави-
симости от значения квантили up=(ln t-µ)/S.
Математическое ожидание наработки до отказа
2/
2
S
e
t
m
+
=
µ
среднеквадратическое отклонение
)1
2
(
2
2
−
+
=
S
e
S
e
t
S
µ
коэффициент вариации
1
2
/ −==
S
e
t
m
t
S
t
ν
При
t
ν <0,3 полагают S
t
≈ν , при этом ошибка <1%.
Часто применяют запись зависимостей для логарифмиче-
ски нормального распределения в десятичных логарифмах.
Соответственно плотность распределения
