Ковалюк Д.О., Москвіна С.М. Моделювання теплотехнологічних об’єктів з розподіленими параметрами

Подождите немного. Документ загружается.

Таким чином, поведінка системи характеризується відображен-

ням:

Ф UV→ (3.13)

Значенням ЛЗ

ij j

aU∈ відповідають нечіткі підмножини

функціями належності ()

∈

, а значенням ЛЗ

ik k

bV∈ – нечіткі

множини

з функціями належності

()

∈

, де ()

FX і ()

– множини нечітких підмножин, що визначені на базових множинах

та

. Відображенню Ф можна поставити у відповідність нечітке

відображення:

:( ) ( )

Ф FX FY→ , (3.14)

яке може бути отримане як нечітка відповідність для всіх

()

∈ ,

()

∈

=×

∪

, (3.15)

де

iij

× ;

iij

× . (3.16)

Вектор значень ЛЗ

′

∈

;

( , ,..., )

bbb b

′

′′

′

при новому наборі

вектора значень вхідних ЛЗ

(, ,..., )

aaa a U

′

′′

′

=∈

визначається на

основі нечіткого логічного висновку. Ця процедура здійснюється з ви-

користанням нечітких підмножин

:[0,1]

′

→

та нечіткої відпові-

дності

Ф . При цьому

′

повинне відповідати вихідній нечіткій відпо-

відності ()

′

∈ , яке визначається як:

′′

 . (3.17)

Якщо

′

є звичайними значеннями, тобто

jj j

axXR

′

∈⊂,

тоді функція належності нечіткої відповідності буде визначатися з

формули:

() ()

ik ij

BBkAj

kK jI

Vy x

μμμ

′

∈∈

∈

⎛⎞

′

=Λ ΛΛ

⎜⎟

⎝⎠

. (3.18)

Враховуючи, те що використання ЛЛМ перевірене на практиці

[134, 149, 152, 153, 157], а проведені дослідження [1, 4, 45, 68, 121] за-

свідчили високі показники адекватності, для моделювання теплотех-

нологічних ОРП було обрано цей вид нечітких моделей.

Технологія побудови нечітких моделей, детально описана в ро-

ботах [120–122], передбачає виконання етапів фазифікації, побудови

нечітких матриць знань, вибору та реалізації алгоритму нечіткого ло-

гічного висновку, дефазифікації вихідного показника.

Побудова нечіткої моделі теплотехнологічного ОРП відноситься

до класу задач не

чітк

ої апроксимації, з дискретним виходом, що фор-

мулюється таким чином:

Задано:

 множину рішень

{}

, , ...,

Ddd d=

, що відповідають ви-

хідній змінній

y ;

 множину вхідних змінних

(

)

, ,...,

Xxx x= ;

 діапазони кількісної зміни кожної вхідної змінної

iii

⎡⎤

∈

⎣⎦

, 1,in= ;

 функції належності, що дозволяють представити змінні

1,in= у вигляді нечітких множин;

 матрицю знань.

Необхідно: розробити алгоритм прийняття рішень, що дозволяє

фіксованому вектора вхідних змінних

****

, ,...,

Xxxx= ,

iii

⎡⎤

∈

⎣⎦

поставити у відповідність рішення

∈

Разом з тим, зауважимо, що теплотехнологічні ОРП суттєво від-

різняються від простих теплових об’єктів, які характеризуються пото-

чними значеннями підтримуваних показників (в основному темпера-

тура і тиск) та їх відхиленнями. Особливістю моделювання теплотех-

нологічних ОРП є, насамперед, взаємозалежність між просторовими

областями об’єкта, тому розглядаючи об’єкт з зосередженими параме-

трами (ан

алогічно до звичайних теплових об’єктів) необхідн

о також

враховувати вплив сусідніх областей по просторових координатах, що

здійснюється за рахунок руху виробів, переміщення теплоносія тощо.

Структурна ідентифікація

Враховуючи той факт, що складність задачі настроювання мо-

делі залежить від кількості параметрів функцій належності, то в робо-

ті запропоновано як функції належності вхідних факторів використо-

вувати гаусівські функції виду:

()

() exp

⎛⎞

−

=−

⎜⎟

⎝⎠

, (3.19)

де

()

– функція належності фактора

нечіткому числу t ; z та c –

параметри функції належності: координата максимуму і коефіцієнт

концентрації відповідно.

Як алгоритм нечіткого логічного висновку обрано алгоритм

Мамдамі [120], який на основі бази знань виду:

jp i i jp j

wxa yd

⎛⎞

⋅= →=

⎜⎟

⎝⎠

∪∩

, 1,

m= , (3.20)

дозволяє визначити належність виходу

y нечіткому терму

d .

Позначивши через ()

функцію належності входу

нечіт-

кому терму

,ijp

a :

()/

ijp jp i i

axx

∫

, [,]

iii

xx∈ , (3.21)

та ()

функцію належності виходу y нечіткому терму

d :

()/

dyy

∫

, [,]yyy∈ , (3.22)

для довільного вектора вхідних даних

(, ,..., )

Xxx x

∗

∗∗ ∗

= отримаємо:

1, 1,

() [ ()]

djpjpi

pk in

Xw x

μμ

∗

=⋅

∨∧

, 1,

m= , (3.23)

де ()

∨∧ – операція з

-норми (t -норми).

Послідовне застосування алгоритму Мамдані до бази знань до-

зволяє обчислити нечітку множину V

для вихідної зміни об’єму па-

лива в заданій точці факторного простору:

()

() () ()

171

,..., , , ...

VV V

Vx x y

dd d

μμ μ

ΔΔ

⎧⎫

ΔΔ Δ

⎪⎪

Δ=

⎨⎬

⎪⎪

⎩⎭

(3.24)

де l– кількість нечітких термів для оцінки змінної V

;

VΔ – назва i -

го терму,

(

)

1, ;

il V

=Δ – ступінь належності змінної VΔ до тер-

му

VΔ ;

d – кількісне значення змінної V

для терму

Параметрична ідентифікація

Як відомо [143], задача настроювання полягає у знаходженні та-

кої математичної моделі F , яка б забезпечувала мінімальне значення

середньоквадратичної нев’язки:

()

() min

RMSE y F X

=−→

∑

, (3.25)

де (,)

XY, 1,iN= – вибірка експериментальних даних, що зв’язує

входи

X з виходом y досліджуваної залежності;

()

– значення

виходу нечіткої моделі при значенні входів, заданих вектором

X .

Позначимо через

P вектор параметрів функцій належності тер-

мів вхідних і вихідної змінної нечіткої моделі і через W – вектор ва-

гових коефіцієнтів правил бази знань, тоді настроювання нечіткої мо-

делі типу Мамдамі зводиться до розв’язання такої задачі математич-

ного програмування: знайти вектор (P,W) щоб :

()

(, , ) min

YFPWX

−→

∑

. (3.26)

Відзначимо, що задача (3.26) відноситься до задач нелінійної

оптимізації, і розв’язується методами математичного програмування.

Таким чином, для моделювання теплотехнологічного ОРП за-

пропоновано використання логіко-лінгвістичних нечітких моделей, з

ієрархічною базою знань, та алгоритмом нечіткого логічного висновку

Мамдані. Для підвищення адекватності моделі пропонується викону-

вати параметричну ідентифікацію параметрів Гаусівських функцій на-

лежності та ва

г правил.

3.2.3. Застосування нечіткої моделі теплотехнологічного

об’єкта з розподіленими параметрами для моделювання тунель-

них печей випалювання

Приклад практичного використання запропонованої структури

нечіткої моделі ТОРП та алгоритму її застосування здійснено для ту-

нельної печі випалювання будівельної кераміки ВАТ “Керамік”, опи-

саної в п.п. 2.2.2.2. Було проведено аналіз факторів, що характеризу-

ють умови протікання теплових процесів на поточній та попередній

позиції, результати якого наведені в табл. 3.1.

Таблиця 3.1.

Фактори процесу випалювання

Назва та опис фактора

– абсолютне відхилення значення вимірюваної температури T

від заданої

Т на поточній позиції печі, °С

– швидкість зміни температури, °С

– теплотворна здатність робочого палива,

/ккал нм

– температура газового середовища попередньої зони, °С

– кількість продуктів горіння, що виноситься в наступну позицію

– витрати палива на поточній позицій печі,

– температура матеріалу в поточній зоні, °С

Відомо [143], що при великій кількості вхідних змінних експер-

ту важко описати причинно-наслідкові зв’язки у вигляді нечітких пра-

вил, більш того, дослідження [120], показали, що якісні бази знань

отримуються, коли кількість входів не перевищує п’яти-шести. Оскі-

льки для нечіткої моделі теплотехнологічного ОПР відібрано 7 факто-

рів, потужність терм множини кожного з яких буде щонайменше 3, то

макси

мальна кі

лькість правил в базі знань по оптимістичним розраху-

нкам буде дорівнювати

3 2187

За цих умов використання звичайних баз є неможливим, тому в

роботі запропоновано для моделювання ТОРП використовувати ієра-

рхічні нечіткі бази знань. Такий підхід, по-перше, дозволяє невеликою

кількістю нечітких правил адекватно описати багатовимірні залежно-

сті “вхід-вихід”, по-друге, подолати “прокляття розмірності”. Крім то-

го, при нечіткому висновку по ієрархічній базі знань відсутні проце-

дури дефазифікації та фазифікації проміжних змінних, тому для опису

проміжних змінних достатньо задати лише терм множини без визна-

чення функцій належності. Враховуючи вищевикладене, в роботі за-

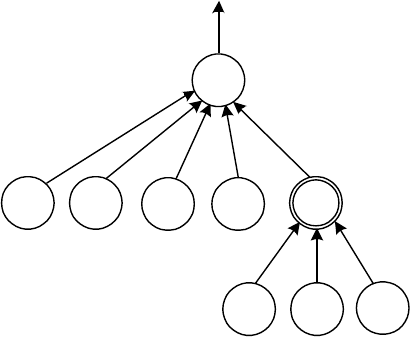
пропоновано ієрархічну класифікацію факторів, подану на рисунку

3.7, з укрупненим фактором

у – кількістю теплоти, що поглинається

в просторовій області моделювання.

Рис. 3.7. Ієрархічна класифікація факторів випалювання

В ієрархічній класифікації факторів використано позначення:

 корінь дерева – зміна об’єму газу ( V

);

 термінальні вершини – фактори впливу (

−

);

 нетермінальні вершини – згортки факторів впливу;

 дуги графу, що виходять з нетермінальних вершин, –

укрупнені фактори впливу (

y ).

Як зазначено в роботах [2, 13], побудова нечіткої бази знань

включає етапи структурної та параметричної ідентифікації, на першо-

му з яких отримуються правила бази та вибирається вигляд функцій

належності, а на другому, з використанням навчальної вибірки та ме-

тодів оптимізації, проводиться оптимізація параметрів функцій нале-

жності та ваг правил.

Розглянемо фазифікацію факторів нечіткої моделі, поданих в

табл. 3.1. Враховуючи вигляд температурної кривої, поданої на рис.

3.1, очевидним є той факт, що нечітка модель може бути використана

для моделювання декількох зон печі з різними значеннями температу-

ри, наприклад, позиції 18–23 (див. рис. 3.1). Оскільки ці позиції харак-

теризуються різними значеннями температур, то для універсальної

множини запропоновано абсолютні та відносні відхилення факторів

x− від своїх номінальних величин (табл. 3.2).

Таблиця 3.2

Фазифікація факторів нечіткої моделі теплотехнологічного ОРП

Назва фактора

Універсал.

множина

Терми для оцінки

VΔ – зміна об’єму газу,

[–100, 100] Висока позитивна (ВП), середня пози-

тивна (СП), низька позитивна (НП),

без змін (БЗ), низька негативна (НН),

середня негативна (СН), висока нега-

тивна (ВН)

– відхилення темпера-

тури, °С

[–75, 75] Високе позитивне (ВП), середнє пози-

тивне (НП), нульове (Н), середнє нега-

тивне (СН), високе негативне (ВН)

– швидкість зміни те-

мператури, °С

[–20, 20] висока позитивна (ВП), середня пози-

тивна (СП), нульова (Н), середня нега-

тивна (СН), висока негативна (ВН)

– теплотворна здат-

ність палива,

/ккал нм

[0, 100] Низька (Н), середня (С), висока (В)

– відхилення темпера-

тури попередньої зони, °С

[–75, 75] Позитивне (П), без відхилення (БЗ),

негативне (Н)

– кількість теплоти, що

витрачається, у.о.

[0, 10] Низька (Н), середня (С), висока (В)

– об’єм повітря, що

виноситься,

мс

[0, 6] Нижче норми (НН), норма (Н), вище

норми (ВН)

– витрати палива, %

[–100; 100] Нижче норми (НН), норма (Н), вище

норми (ВН)

– відхилення в темпе-

ратурі матеріалу, °С

[–60, 60] Нижче норми (НН), норма (Н), вище

норми (ВН)

Такий підхід дозволяє зробити нечітку модель універсальною і

застосовувати для моделювання будь-якої позиції печі. Як приклад

розглянемо фазифікацію виходу моделі – .V

Згідно з конструктив-

ними особливостями та технологічним регламентом кількість газу, що

подається на пальники, може варіюватися від 40 до 180 мм. вод. ст.

[133] і встановлюється в залежності від підтримуваної температури:

так на позиції № 6 ( 880T = °С, див. рис. 3.1) витрати палива в статич-

ному режимі становлять 150 мм. вод. ст., на позиції № 20 ( 950T = °С,

див. рис.

3.1) – 180 мм. вод. ст. В цьому випадку універсальна мн

ожи-

на для функцій належності задається у відсотках [–100; 100], де уні-

версальна множина [0; 100], містить значення

max ном

−

, а [–100; 0]

включає діапазон значень

minном

−

Структурна ідентифікація. Для моделювання укрупненого фа-

ктора

використовується експертна нечітка база знань типу Мамда-

ні, наведена в табл. 3.3.

Таблиця 3.3

Матриця знань для проміжного фактора

y нечіткої моделі

НН Н Н Низька

НН ВН Н Низька

НН Н ВН Низька

НН ВН ВН Низька

Н ВН Н Низька

НН НН Н Середня

НН НН ВН Середня

Н Н Н Середня

Н ВН ВН Середня

Н Н ВН Середня

ВН ВН ВН Середня

ВН ВН Н Середня

Н НН Н Висока

Н НН ВН Висока

ВН Н Н Висока

ВН Н ВН Висока

ВН НН Н Висока

ВН НН ВН Висока

Для підвищення прозорості нечіткої моделі та зменшення кіль-

кості правил в ієрархічній базі знань в роботі запропоновано такий

спосіб. Якщо ступінь належності значення фактора

∗

, що характери-

зує відхилення температури ()et , до термів високе негативне (ВН) або

високе позитивне (ВП), є найбільшою серед усіх термів, то викорис-

товується наведена в табл. 3.4 спрощена база знань, яка враховує лише

фактори

Таблиця 3.4

Нечітка база знань при високих відхиленнях температури

()et

ВП СП Н СН ВН

ВП ВН ВН ВН СН СН

ВН СП ВП ВП ВП ВП

На перетині відхилення температури ()et та зміни температури

знаходиться значення VΔ , що вказує на зміну об’єму газу. Заува-

жимо, що правила в табл. 3.4 не потребують настроювання, а точне

значення зміни об’єму газу V

визначається як координата максиму-

му відповідної функції належності.

Якщо ступінь належності значення фактора

∗

, до термів висо-

ке негативне (ВН) або високе позитивне (ВП), не є максимальним, то

використовується база знань, що включає фактори

−

y , наведе-

на у додатку А.

Параметрична ідентифікація. Для проведення параметричної

ідентифікації використовувалася навчальна вибірка, сформована з

статистичних даних наступним чином: фіксуються всі значення вимі-

ряних факторів

x− і об’єм газу, встановлений для зміни поточної

температури. Оскільки вимірювання температури проводиться із за-

даною періодичністю, то через певний інтервал часу фіксується нове

значення температури цієї позиції і розраховується значення TΔ . Та-

ким чином, навчальна вибірка показує на скільки зміниться темпера-

тура зони через певний інтервал часу, при зміні об’єму газу на VΔ (за

сталих значен

ь всіх інших факторів), і є

сукупністю пар типу

{, , }Tx x VΔ−Δ. Зауважимо, що оскільки нечітка модель виражає

залежність об’єму газу від температури, то навчальна вибірка без

втрати адекватності трансформується до виду

(

)

... ,VFxx T

=Δ.

Відомо, що адекватність розробленої нечіткої моделі залежить в

першу чергу від співвідношення параметрів, що підлягають настрою-

ванню та розміру навчальної вибірки. Експериментальні дослідження,

проведені в [143], показали, що гарні результати оптимізації отриму-

ються в тому випадку, коли об’єм навчальної вибірки в 2 і більше ра-

зів перевищує кількість параметрів настроювання. Тому для визна-

чення об’єму навчальної вибірки розрахуємо кількіст

ь пара

метрів, що

підлягають настроюванню. В нечіткій моделі теплотехнологічного

ОРП будемо настроювати параметри функцій належності для факторів

x− ,

y , та вихідної величини V

(загальна кількість термів 24).

Зазначимо, що настроювати терми “високе позитивне” та “високе не-

гативне” змінної

не має потреби, оскільки вони використовуються

в окремому випадку, наведеному в табл. 3.4.

Використаємо як параметри настроювання такі величини:

 24 коефіцієнта концентрації функцій належності термів вхід-

них і вихідної змінної;

 12 координат максимумів функцій належності. Координати

максимумів функцій належності крайніх термів кожної змінної не на-

строюються, оскільки передбачається, що вони будуть дорівнювати

межам діапазонів, в яких лежать значення змінних.

Таким чином, загальна кількість настроюваних параметрів дорі-

внює 36, а тому розмір навчальної вибірки становить 75 значень.

Побудова нечіткої моделі проводилися з використанням пакета

Matlab в інструментарії Fuz

zy LogicToolbox. Враховуючи те, що в

Fuzzy LogicToolbox не передбачене настроювання моделей типу Мам-

дані, тому оптимізація ваг правил здійснювалась програмним шляхом

з використанням пакета Optimization Toolbox, на основі підходу, за-

пропонованого в роботі [143]. Лістинг програми наведений в додатку

Б. В результаті оптимізації отримано значення параметрів функцій на-

лежності, наведені в таблиці 3.5 та вагові коефіцієнти правил бази

знань, подані разом з пр

авилами в додатку

А.