Ковалюк Д.О., Москвіна С.М. Моделювання теплотехнологічних об’єктів з розподіленими параметрами

Подождите немного. Документ загружается.

Таблиця 3.5

Результати оптимізації параметрів функцій належності

Фактор Тер

Коеф.

концентр.

Коеф.

максим.

Фактор Терм Коеф.

концентр.

Коеф.

максим.

ВП 10 –75

П 23,561 75

СП 6,441 –36.075 БВ 7,720 20

Н 4,501 13,813 Н 22,054 –75

СН 4,889 36,164

Н 3,434 0

ВН 2,533 75 С 4,818 6,718

ВП 4,526 –20 В 4,606 10

СП 1,939 –8,641

ВП 10,795 –100

Н 3,308 –1,433 СП 5,308 –57,624

СН 7,478 7,950 НП 14,960 –8,364

ВН 1,303 20 Н 3,595 4,061

Н 19,403 0 НН 4,761 19,505

С 14,242 63,184 СН 2,496 60,994

В 18,450 100 ВН 11,086 100

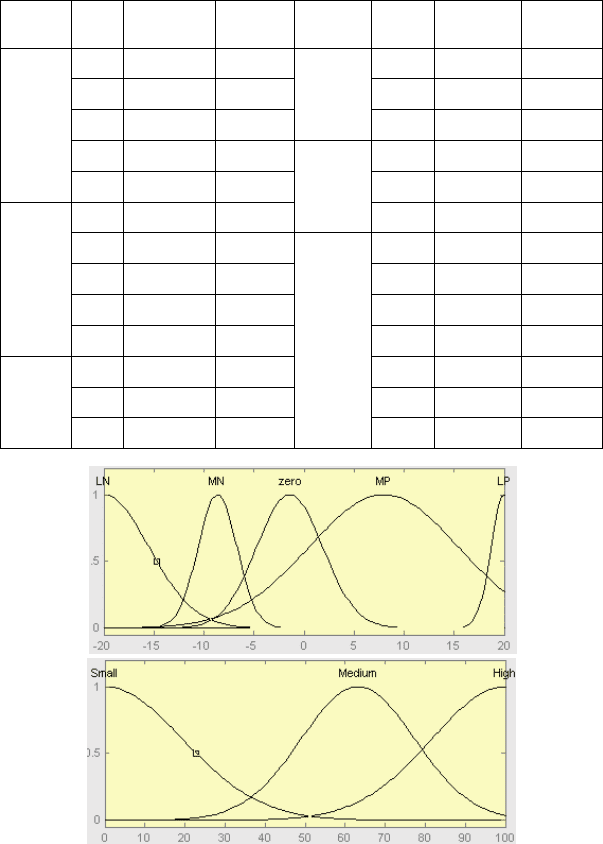
Рис. 3.8. Функції належності факторів

та

Аналіз отриманих результатів, часткове представлення яких в

графічному вигляді подане на рис. 3.8, свідчить про відсутність таких

типових порушень втрати прозорості моделі як: неінтерпретабельність

крайнього терма, втрата лінійної впорядкованості терм множин, не-

відмінність функцій належності деяких нечітких множин [144]. За да-

ними навчальної вибірки за формулою (3.25) розрахована середня

квадратична нев’язка, що складає 9,59.

Таки

м чином, формалізовано нечітку модел

ь теплотехнологіч-

ного ОРП на прикладі тунельної печі випалювання, та проведено оп-

тимізацію її параметрів, що дозволяє більш точно здійснювати моде-

лювання цього об’єкта.

3.3. Дослідження адекватності нечіткої моделі

Перевірку адекватності розробленої нечіткої моделі теплотехно-

логічного ОРП можна здійснити двома способами, перший з яких по-

лягає у використанні контрольної вибірки для розрахунку нев’язки,

що служить показником точності і є аналогом середньоквадратичного

відхилення. Другий спосіб оснований на проведенні експерименталь-

них досліджень та порівнянні експериментальних та розрахункових

значень.

В роботі пропонується вико

ристати другий підхід, оскільки він є

більш достовірним і наближеним до реальних умов застосування мо

делі. З іншої сторони використання такого підходу не супроводжуєть-

ся труднощами, оскільки оснащеність виробництв сучасними автома-

тичними системами управління, дозволяє дистанційно отримати всі

необхідні для дослідження моделі дані за допомогою ЕОМ робочого

місця оператора.

Експериментальні дослідження були проведені на ВАТ “Кера-

мік” з використанням вс

тановлен

ої автоматизованої системи управ-

ління, розробленої Інститутом Газу України [112].

Дослідження моделі проведено для теплового режиму 15-ї зони

випалювання за алгоритмом, зображеним на рис. 3.6. Параметри ста-

тичного режиму 15-ї зони випалювання наведені в табл. 3.6. Зауважи-

мо, що значення наведених в табл. 3.6 факторів періодично вимірю-

ються контрольно-вимірювальними приладами, а як управляючий

вплив виступає об’єм газу, що подається на пальники, та відповідна

пропорційно розрахована кількість повітря.

Таблиця 3.6

Характеристики позиції № 15 в статичному режимі

Назва Значення

Підтримувана температура, °С 800

Температура наступної зони, °С 840

Об’єм газу, . .

мводст

180

Об’єм повітря, що виноситься,

0,04

Температура матеріалу, °С 750

Теплотворна здатність палива Норма

Характеристикою точності моделі обрано середнє квадратичне

відхилення між прогнозованою та реальною температурою, що вста-

новиться через певний проміжок часу за відповідної кількості палива.

(())

TTt

∗

=−

∑

, (3.27)

де N – кількість вимірювань, що здійснюються через інтервал часу t ;

∗

– значення температури, розраховані по моделі; ( )Tt – значення

реальної температури в момент часу t .

Перевірка адекватності моделі проводилася за таким алгорит-

мом:

Вимірювалися значення параметрів моделі в момент часу t .

За значеннями виміряних параметрів визначалося, чи необ-

хідно змінювати об’єм газу V . Якщо так – встановлювався новий

об’єм газу VV V=+Δ.

За моделлю розраховувалося значення температури

∗

, що

встановиться через інтервал часу t

при об’ємі газу V .

Через інтервал часу t

вимірювалося значення температури

()Tt, яке порівнювалося із прогнозованим значенням T

∗

Дослідження були проведенні за такою схемою:

 інтервал часу, через який вимірюються значення параметрів

моделі та температура T – 180 с;

 кількість дослідів – 5, для більш точного врахування стану

системи;

 кількість вимірювань у кожному досліді – 10.

Графічна інтерпретація експериментальних досліджень для од-

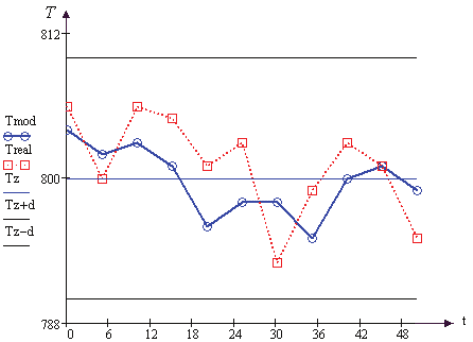
нієї серії дослідів подана на рис. 3.9.

Рис. 3.9. Дослідження зміни температурного поля

Використовуючи результати експериментів, з експерименталь-

них даних була розрахована середня квадратична нев’язка моделі, яка

становить 9.64, та середнє квадратичне відхилення температури, що

становить 18,3. Наведені показники точності повністю підтверджують

адекватність запропонованої моделі.

Таким чином, розроблена математична модель є адекватною ре-

альним (ВАТ “Керамік”) даним і може бути в

икористана на практиці

для моделювання теплотехнологічного ОРП. Крім того

, вона дозволяє

запобігти існуючим коливанням та підтримувати стабільний рівень

температурної кривої

(,)

tT .

Розроблена на основі цієї моделі інтелектуальна система прой-

шла тестування і визнана спеціалістами працездатною в умовах су-

часного виробництва, про що свідчить акт її впровадження.

Для використання розробленої моделі теплового технологічного

об’єкта з розподіленими параметрами в реальному масштабі часу не-

обхідно оцінити її складність та точність. Відомо [70], що викорис-

тання математичної моделі безпосередньо для моделювання об’єкта

досліджень передбачає її подання у вигляді деякого алгоритму, який

реалізовується програмним чи апаратним шляхом. Для оцінки склад-

ності алгоритмів на сьогодні найбільш поширеним підходом є асимп-

тотичний аналіз [8, 29], метою якого є порівняння витрат часу та ін-

ших ресурсів різними алгоритмами, призначеними для розв’язання за-

дачі, при різних об’ємах вхідних даних. Враховуючи те, що в розроб-

леній мат

ематичній моделі кількість вхідних

даних є сталою величи-

ною, то для оцінки складності алгоритму її обчислення будемо вико-

ристовувати обчислювальну модель нерозгалуженої програми, в якій

за допомогою прийому розгортання циклів вдається уникнути команд

розгалуження і зали

шити лише арифмет

ичні операції. В цьому випад-

ку обчислювальною складністю алгоритму виступає число арифмети-

чних операцій

(())

Ofn.

Розглянемо алгоритм, що реалізує, нечітку модель теплового

ОРП:

розрахунок належності значення вхідного фактора моделі до

кожного з термів, що описують цей фактор;

розрахунок значення правила та його належності до відпові-

дного терма вихідної величини;

нечіткий логічний висновок та знаходження належності ре-

зультату до кожного з термів вихідної величини;

дефазифікація вихідної величини.

Розглянемо наведені етапи алгоритму з точки зору кількості

арифметичних операцій, необхідних для їх виконання. Належність

вхідного значення фактора до кожного з термів, що описують цей фа-

ктор розраховуються з формули (3.19), для якої необхідно виконати 6

операцій суми, 1 операцію ділення та 1 операцію піднесення до

степеня.

Розрахунок значення правила фактично є операцією знаходжен-

ня мініму

му в одновимірному масиві, і, як показано в

[8], здійснюєть-

ся не менше ніж за 1n− порівняння. Тоді, для обчислення кількості

теплоти, що витрачається, необхідно використати 3 порівняння для

кожного з 18 правил, а для визначення об’єму газу – 5 порівнянь для

28 правил.

Операцію нечіткого логічного висновку типу Мамдані можна

представити як операцію знаходження максимальних елементів в од-

новимірних масивах, довжина яких дорівнює кількості правил, а кіль-

кість відповідає кількості термів, що описують вихідну величину. Та-

ким чином, для нечіткого логічного висновку кількості теплоти, що

витрачається, необхідно виконати 318 54

⋅

= , а для визначення об’єму

газу 728 196⋅= операцій порівнянь.

Процедура дефазифікації складається із операції ділення, n опе-

рацій множення і 2n операцій додавання, де n – кількість точок дис-

кретизації термів вихідної величини.

Для оцінки відносної швидкодії розробленої моделі порівняємо

її з моделлю (2.25), наведеною в роботі [28], і розв’язаною з викорис-

танням дискретизації моделі та подальшим розв’язанням сист

еми ал-

гебраїчних рівнянь. Для

порівняння швидкодії нечітка модель тепло-

технологічного ОРП була реалізована програмно на мові програму-

вання Object Pascal. Результати дослідження кінцево-різницевої моде-

лі взяті з табл. 2.1, порівняння характеристик моделей наведено в

табл. 3.7.

Таблиця 3.7

Результати дослідження часової складності моделей ОРП

Модель ОРП

Розрахунок однієї

зони

,t с

Метод моделювання ОРП (14

зон, 5 ОЗП) ,t с

Нечітка модель 1,5 комбінований 9225,39

Кінцево-різницева

модель

2,4

кінцевих різниць 14338,94

42,172

1024,21

Таким чином, з таблиці 3.7 можна зробити висновок, що засто-

сування нечіткої моделі дозволяє значно підвищити ефективність мо-

делювання теплотехнологічного ОРП.

4. МЕТОД ВИЗНАЧЕННЯ ОПТИМАЛЬНИХ

ПАРАМЕТРІВ МОДЕЛІ ТЕПЛОТЕХНОЛОГІЧНОГО ОБ’ЄКТА

З РОЗПОДІЛЕНИМИ ПАРАМЕТРАМИ

Теплотехнологічний об’єкт з розподіленими параметрами зазви-

чай є складовою частиною певного технологічного процесу. З огляду

на це для підвищення адекватності математичної моделі ТОРП доці-

льно здійснити уточнення значень її параметрів в залежності від пото-

чного стану всього ТП.

В цьому розділі задача уточнення параметрів моделі теплотех-

нологічного ОРП розглядається на прикладі ту

нельної пе

чі випалю-

вання будівельної кераміки.

4.1. Загальна схема методу визначення оптимальних параметрів

моделі теплотехнологічного об’єкта з розподіленими параметрами

на прикладі процесу випалювання

Проведений аналіз математичних моделей процесу випалювання

показав, що їх використання є цілком виправданим та перевіреним на

практиці. Проте ці моделі не дозволяють забезпечити максимальну

ефективність процесу випалювання [101], яка визначається співвід-

ношенням між якістю кінцевої продукції та витратами для її отриман-

ня. Типовим прикладом виступають випадки отримання виробів низь-

кої якості при високих енергетичних витратах [49

, 63].

Основна причина такої невідповідності

полягає в тому, що для

діючих АСУТП ключовим є питання підтримання заданої температу-

рної кривої

(,)

(де

– номер позиції печі), розрахованої на етапі

проектування печі. Проте власні дослідження авторів, проведені на

діючих АСУТП, а також результати робіт [63, 79, 94, 135] показали,

що процес випалювання формує показники якості продукції та визна-

чає основні економічні витрати, а тому при його моделюванні необ-

хідно врахувати фактори всього технологічного процесу, починаючи

від формування виробів і закінчуючи показниками якос

ті продукції,

тобто вирішувати за

дачу пошуку оптимального температурного ре-

жиму випалювання для поточного стану процесу. Це дозволить здійс-

нювати оперативне реагування (настроювання параметрів процесу) на

збурюючі впливи, пов’язані зі зміною температури і вологості повітря

для охолодження, теплотворної здатності природного газу, властивос-

тей сировини, відхиленнями в підготовці напівфабрикату виробів, ді-

ями обслуговуючого персоналу та технологічного обладнання.

Для розв’язання цієї задачі в роботі запропоновано метод ви-

значення оптимальних параметрів моделі теплотехнологічного ОРП з

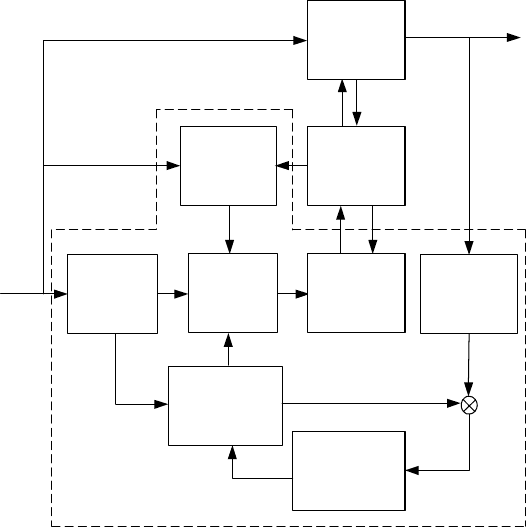
урахуванням поточного стану ТП, структурна схема якого показана на

рис. 4.1.

Продукція

Модель

коригування

температури

Визначення

якості

Модель

оптимізації

Модель

ТОРП

Блок

управління

Модель

прогнозування

якості

Модель

визначення

класу

продукції

Уточнення

моделі

прогнозування

якості

Об'єкт

управління

реал

прогн

opt

Підсистема моделювання

Рис. 4.1. Структурна схема методу

Ідея методу полягає в тому, що на основі значень параметрів ТП

необхідно спрогнозувати максимально можливий клас якості продук-

ції і знайти оптимальні в сенсі енергетичних витрат значення темпера-

турного поля – уточненні параметри моделі теплотехнологічного

ОРП, при яких досягається цей клас якості. Такий підхід є можливим

завдяки чіткому технологічному регламенту проходження ТП, послі-

довності етапів та взаємозалежності їх результатів, наявності контро-

льних точок для отримання необхідної інформаційної бази.

Враховуючи опис технологічного процесу виготовлення будіве-

льної кераміки (п.п. 2.2.2.1), тунельної печі випалювання (п.п. 2.2.2.2)

та моделі прогнозування якості продукції (п.п. 2.2.2.3), розглянемо

принцип дії запропонованого методу.

Для процесу виготовлення будів

ел

ьної кераміки згідно з ДСТУ

марка міцності цегли (клас якості) присвоюється на основі потраплян-

ня усередненого значення міцності виробів у відповідний інтервал

(див. табл. 2.2). Так, наприклад, для марки виробів “125” середнє зна-

чення міцності повинне знаходитися в інтервалі [100;125), причому

мінімальні енергетичні витрати для отримання цієї марки будуть у ви-

падку, якщо значення міцності дорівн

юватиме нижній границі даного

інтервалу – 100 МПа.

Тому згідно з запропонованим методом необхідно знайти такі

параметри температурного поля, при яких досягається нижня межа

максимально можливого класу міцності виробів.

Метод визначення оптимальних параметрів моделі теплотехно-

логічного ОРП працює за таким алгоритмом:

Прогнозування максимально можливого класу якості проду-

кції на основі поточного стану ТП (блок “Модель визначення класу

продукції”, рис. 4.1).

2. Знаючи максимально можливий клас якості, знаходиться ни-

жня межа міцності для цього класу (див. табл. 2.2). З використанням

моделі всього технологічного процесу (блок “Модель прогнозування

якості”) та моделі оптимізації (блок “Модель оптимізації”)

розв’язується за

дача оптимізації відносно

значень температурного

поля

(()) min

→TU , (4.1)

max

min

max

min max

_(,)

CLASS

MM Class Class

MM Mitsnist M

⎧

⎪

⎨

⎪

≤≤

⎩

WWW

, (4.2)

де (())

TU – критерій ефективності, що враховує зв’язок між темпе-

ратурою та енергетичними витратами для її підтримання; _

MClass

– математична модель класифікації якості виробів; _

M Mitsnist –

математична модель ТП виготовлення кераміки;

H – вектор парамет-

рів сировини та етапів підготовки виробів;

min

W ,

max

W – нижні і вер-

хні межі технічних параметрів системи керування

3. Уточнені параметри моделі теплотехнологічного ОРП –

opt

T ,

отримані на попередньому кроці, використовуються в моделі управ-

ління теплотехнологічним ОРП (блок “Модель ТТОРП”) для моделю-

вання температурного поля об’єкта управління та реалізуються бло-

ком управління.

4. У випадку неможливості підтримання розрахованої темпера-

турної кривої з технічних причин (наприклад, зміна режиму проштов-

хування виробів, вихід з ладу пальників на окремих позиціях, тощо) в

методі передбачена можливі

сть операт

ивного коригування температу-

рного поля за допомогою моделі коригування температурного поля

(блок “Модель коригування температури”).

5. Після завершення процесу випалювання визначається реальна

якість продукції

реал

Q (блок “Визначення якості”) та порівнюється з

прогнозованою якістю

прогн

Q . У випадку, якщо різниця

реал

Q –

прогн

перевищує задане граничне відхилення, виконується процедура кори-

гування моделі прогнозування якості (блок “Уточнення моделі про-

гнозування якості”) з використанням нових даних ТП.

Таким чином, для реалізації методу необхідна розробка моделі

класифікації марки виробів, моделі прогнозування якості, моделі ко-

ригування температури та вибір критерію оптимізації, що враховує

зв’язок енергетичних витрат і темп

ератури.

4.1.1. Логіко-імовірнісна модель класифікації марки виробів

Для побудови математичної моделі прогнозування класу міцно-

сті виробів проаналізуємо існуючі методи класифікації та можливість

їх застосування до цієї задачі. Нехай

– вектор параметрів сировини

та випалювання, W – кількість марок цегли, тоді задача класифікації