Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 99

Cr = 0

(25)

and due to eqs.(21)

Ar = 0.

(26)

We may also assume that the latter case is satisfied if |A|=0 which implies

Ar = 0 (r ≠ 0). (27)

Analytically eq.(27) is written as follows:

ĮĮ...ĮĮ

...............

ĮĮ...ĮĮ

nn2n1

n21-n,22221

n11-n,11211

−

(28)

or in a partitioned form

n21

1211

(29)

where A

is an (n−1)×(n−1) non-singular symmetric matrix, A

an n×1 (column)

matrix such that

; α

is a real (scalar) quantity,

=(r

,..., r

n−1

)

is a vector

and r

the n

component of the vector r. From eq.(29) one can find

= −r

−

≠0).

(30)

Introducing this expression of

into eq. (25) we obtain

nn21

1211

(31)

where

⎥

⎦

⎤

⎢

⎣

⎡

−−−

−

1n1,n1,1n

1n1,11

.........

c...c

⎥

⎦

⎤

⎢

⎣

⎡

− n1,n

2112

(32)

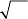
100 A.N. Kounadis

From eq. (31) it follows that

0cr2r

=++ CC

2111

(33)

or due to eq.(30)

0c2

nn12

112112

1111

=+−

−−−

AACAACAA

(34)

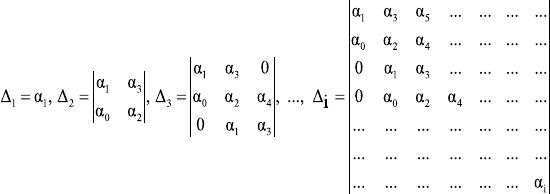
Eq. (34) along with the determinantal equation

|A| = 0 (35)

furnish a non-linear system of two equations with unknowns λ and μ

which can

be solved numerically provided that the matrix C and all parameters are known.

The lowest positive λ(<

) is the dynamic instability load λ=λ

which corre-

sponds to a

generic Hopf bifurcation. This is so because the transversality condi-

tion is also satisfied according to the proof given above.

4 Νon-conservative Systems

We consider the above autonomοus, weakly damped, system subjective now to a

partial

follower (step) load with η≠1 (nonconservative system). Then, the general-

ized stiffness matrix V=V(λ; k

ij,

η) is asymmetric and hence the previous outlined

procedure with η=1 is not applicable. However, one can overcome such a diffi-

culty by employing either the very efficient

asymptotic stability criterion of Lié-

nard- Chipart [16] or to render the system

symmetric through suitable matrix trans-

formations. Subsequently, both procedures will be presented.

4.1 Liénard-Chipart Stability Criterion

Consider the general case of a polynomial in z with real coefficients α

(i=0,1,…,n)

0z...zz)z(f

n1n

=α+α++α+α=

−

()

>α

(36)

We will seek the

necessary and sufficient conditions so that all its roots have

negative real parts. Denoting by z

(κ = 1,…, m) the real and by r

± is

(j = 1,…,

(n-m)/2; i=

1−

) the complex roots of eq.(36) we may assure that all these roots in

the complex plane lie to the

left of the imaginary axis, i.e.

<0, r

<0 (κ=1,…,m; j=1,…,(n-m)/2) (37)

Then one can write

()

∏∏

−

++−−=

1κ

κ0

srz2rzzzαf(z)

(38)

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 101

Since due to inequality (37) each term in the last part of eq.(38) has

positive coef-

ficients, it is deduced that

all coefficients of eq.(36) are also positive. However,

this (i.e. α

>0 for all i with α

>0) is a necessary but by no means sufficient condi-

tion for all roots of eq.(36) to lie in the left half- plane (i.e. Re(z)<0).

According to Routh–Hurwitz criterion [15, 16] for

asymptotic stability, i.e. for

all roots of eq.(36) to have negative real parts the

necessary and sufficient condi-

tions are

>0, ……, Δ

> 0 (39)

where

(40)

where Δ

(with α

=0 for κ>n) is the Hurwitz determinant of order i (i = 1,2,…,n).

It should be also noted that when the above necessary conditions α

>0 (for all i)

hold, inequalities (39) are not independent according to Liénard and Chipart who

established the following elegant criterion for asymptotic stability [16].

The Liénard – Chipart asymptotic stability criterion

Necessary and sufficient conditions for all roots of the real polynomial

()

0,0z...zz)z(f

0n1n

>α=α+α++α+α=

−

to have negative real

parts

can be given in any one of the following forms:

1. α

>0, α

n-2

>0,...; with

⎩

⎨

⎧

>Δ>Δ

...,,0,0or

...,,0,0either

(41a)

2. α

>0; α

n-1

>0, α

n-3

>0,...; with

⎩

⎨

⎧

>Δ>Δ

...,,0,0or

...,,0,0either

(41b)

This asymptotic stability criterion was rediscovered by Fuller [21].

4.2 Symmetrization of Asymmetric Matrices

If the generalized stiffness matrix V

is asymmetric one should adopt the procedure

that follows after recalling some theorems from

the theory of matrices. A real

asymmetric matrix A (

≠A

) is symmetrizable if it can be expressed as the product

two symmetric matrices one of which is positive definite [6], i.e.

A = S

(42)

102 A.N. Kounadis

where S

is positive definite and

SS =

(symmetric matrix). Clearly, from rela-

tion (42) it is deduced

SAS =

−

which indicates that a symmetrizable matrix

becomes

symmetric after multiplication by an appropriate positive definite matrix.

Moreover, since a symmetrizable

matrix is similar to a symmetric matrix, its ei-

genvalues are necessarily

real.

From (ρ

Μ+ ρ C+V)r= 0 it follows that

(

=+ρ+ρ rVCIM

(

=+ρ+ρ rVCI

(43)

where

CMC

−

and

VMV

−

One can find transformations of the form

TSCSSV

121

β==

(44)

where S

is a positive definite matrix, S

and T are symmetric matrices, while β is

a small positive number.

Using relations (44) ,eq.(43) is written as follows

0)(

211

=+βρ+ρ rSSTSI

0)(

2/1

=+βρ+ρ

−

rSSTSS

(45)

0)(

2/1

=+βρ+ρ

−

rSSSSSTSI

(46)

where

2/1

and

2/1

−

are also symmetric matrices, since S

is a symmetric

matrix.

Similarly from (ρ

Μ+ ρ C+V)r= 0 one can write

0)(

211

=+βρ+ρ SSTSIMq

0)(

2/1

22/1

=+βρ+ρ

−

SSSSSTSISMq

(47)

0)(

2/1

22/1

=+βρ+ρ SSSSTSISMq

(48)

The transpose of eq.(48) is

0)(

T2/1

2/1

=+βρ+ρ qMSSSSSTSI

(49)

Comparing eqs(46) and (49) we obtain

qMSrS

2/1

−

qMSr

(50)

Using eqs(44) one can write

SVS =

−

TβC

−

(51)

where S

and T are (as stated above) symmetric matrices, while S

is a positive

definite matrix. Note that transformations of the form (44) are not always possible

for systems with more than three degrees of freedom.

Subsequently the procedure for a conservative symmetric system outlined

above can be established.

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 103

5 Numerical Results

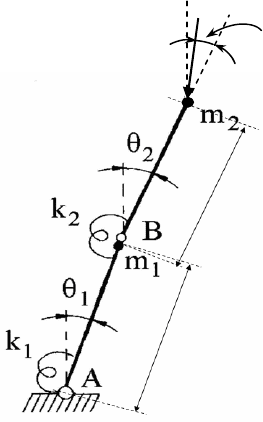
Since numerical results are available from previous studies [4, 12, 13, 14, 18]

which are based on 2 or 3-DOF models for the sake of comparison we will use the

spring cantilevered dynamic model of 2-DOF shown in Fig.2 under a partial fol-

lower load with noncocervativeness parameter η≠1 (nonconservative system) as

well as for η =1 (conservative system). Numerical results will be presented in

graphical (mainly) but also in tabular form. Moreover, attention will be focused on

the effect of the

violation of one or more of the conditions of the Liénard-Chipart

asymptotic stability criterion.

Fig. 2. 2-DOF autonomous cantilever model under a partial follower load P.

The response of this dynamic model, carrying two concentrated masses, is stud-

ied when it is either

unloaded or loaded by a suddenly applied load of constant

magnitude and varying (η≠1) or constant (η=1) direction with infinite duration.

Such an autonomous dissipative system with

infinitesimal damping (including the

case of zero loading) is properly discussed. If at least one root of the secular eq.(6)

has a

positive real part, the corresponding solution (7) will contain an exponen-

tially increasing function and the system will become

unstable. The nonlinear

equations of motion for the 2-DOF nonconservative model of Fig.2 with rigid

links of equal length

l are given by Kounadis [12].

0Vșcșc)șsin(ș)școs(șșșm)(1

121211121

22121





+ș

0Vcc)sin()cos(

211222221

12112

TTTTTTTTT



(52)

ηθ

104 A.N. Kounadis

where

[]

21211

1)θ(ηθλsinθk)θ(1V −+−−+=

2,122

λsinηθθθV −−=

and η

is the nonconservativeness loading parameter, m=m

, k=k

and

λ=Pl/k

Linearization of eqs.(52) after setting

ρρ

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=Θ

gives

(

)

VCM +ρ+ρ

φ = 0 (53)

where

−−

−−−−+

ȜȘ11

1)Ȝ(Ș1Ȝ1k

1m1

2221

1211

2212

1211

2212

1211

(54)

The

static buckling (divergence) equation is given by

ηλ

− η(2 + k)λ + k = 0 (55)

whose lowest root is the

first buckling load

λ equal to

= 0.5[k + 2 −

4k/η2)(k

−+

]

(56)

which for real roots yields η=4k/(k+2)

that defines the boundary between the

region of

existence and non-existence of adjacent equilibria.

Ιn case of a Rayleigh’s dissipative function the damping coefficients are,

= c

, c

= −c

, c

= −c

and c

= c

, where c

(i=1,2) is dimensionless coef-

ficient for the

ith rigid link. This case (for which detC=c

) is a specific situation

of the damping matrix

C which is not discussed herein.

5.1 Conservative System (η=1)

The corresponding equations of motion are obtained for the 2-DOF conservative

model from eqs(52) after setting η=1. Thus eqs(53&54) are also valid after insert-

ing η=1 into matrix

V and

λ .

For a

degenerate Hopf bifurcation (Fig.1b), associated with a positive semi-

definite matrix C, using eqs(15) and (16) for n=2, we get

r = r

=−c

(57)

Application of eq.(19) due to eqs(54) gives

()

λ1r

1rm1

1rλ1k

−+−

−−+

(58)

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 105

from which we obtain the degenerate Hopf bifurcation load λ = λ

, i.e.

− mr − 1)λ

= r

(m + k + 2) + r(k − m) − 2, (59)

where m and k are positive quantities, while r may be positive or negative. Note

that if r

−mr−1=0, the critical load λ

exhibits a discontinuity (varying from +∞ to

−∞). For r

(m+k+2)+r(k−m)−2=0 it follows that λ=0. Clearly, for given r the

above extreme values of λ

may occur for various combinations of values of the

parameters m and k.

It is worth noticing that the

discontinuity in the flutter load λ

(being independ-

ent of the stiffness ratio k) occurs at m=(r

−1)/r. Namely, for a given damping

ratio r, one can find a critical value of m, i.e. m=m

, which corresponds to a dis-

continuity

in the load λ

. As stated above, since r(=−c

) does not depend on λ,

eq.(9) yields dν/dλ=0 (violation of the transversality sufficient condition for a de-

generate Hopf bifurcation).

From eq.(19) we obtain

λ1r

ρμ

−+−

=−=

(r≠0)

(60)

For the above 2-DOF model with k = 1, m = 10 and a positive semi-definite ma-

trix

C with c

= 0.01, c

= c

= 0.002 and c

= 0.0004 (i.e. |C|=0) we find

0.381966011 r = −0.20, λ

= 0.32/1.04 = 0.307692307, and ρ

= −μ

=−1.115384615

[4]. The

critical mass ratio for which a discontinuity in the flutter load λ

for this

degenerate Hopf bifurcation occurs for m

= 4.80.

For a

generic Hopf bifurcation (Fig.1c), associated with a given indefinite ma-

trix C, according to the exact analysis, one can obtain λ

and μ

by solving the

system of eqs.(23). The discontinuity in the flutter load λ

in the above degenerate

Hopf bifurcation appears also in generic Hopf bifurcations a shown below.

In case of an indefinite matrix

C for which |C|< −ε

with ε→0, the determina-

tion of the flutter load λ

(and then μ

) is appreciably simplified without diminish-

ing its accuracy.

Thus, application of eq.(19) gives

2212

1211

MrM

VrV

MrM

VrV

(61)

which leads to eq.(58) and then to eq.(59). The ratio r is obtained from eq.(25), i.e.

+ 2c

r + c

= 0,

()

2211

1212

cccc

r −±−=

(62)

Clearly, the equation yielding a

discontinuity in the flutter load λ

, i.e. r

−mr−1=0, is

still valid. For the above 2-DOF model with k=1 and m=10 related to an indefinite

matrix

C with c

=0.01, c

=0.0325 and c

=0.012 (i.e. |C|=−9.3625×10

−4

<0) we

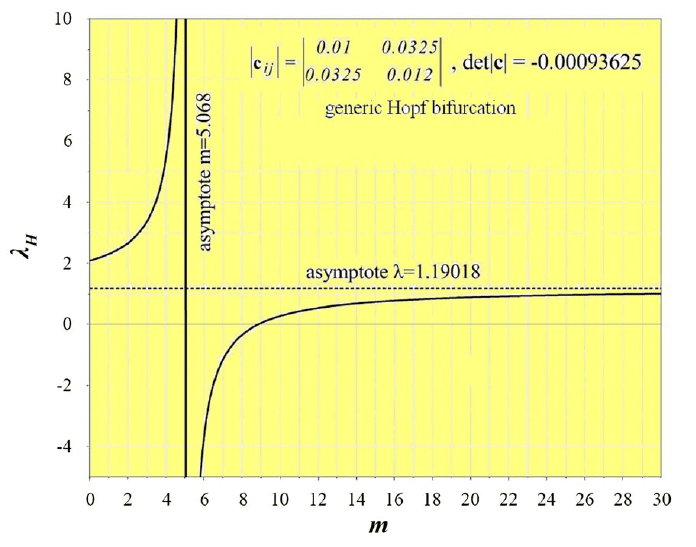
106 A.N. Kounadis

find, according to the exact analysis, λ

=0.193698381<

, and μ=1.109221303 [4].

On the basis of the

approximate analysis we obtain using eq.(62) r=−0.190179743

and thereafter through eq.(61), λ

=0.193830151 and μ=1.109204333, respectively,

which practically coincide with the previously found values of λ

and μ. The plot λ

versus m>0 with the corresponding asymptotes m=5.068 and λ=1.19018 is shown in

Fig.3.

Fig. 3. Variation of λ

versus mass ratio m for stiffness ratio k=1 with a discontinuity of the

flutter load λ

for m=5.068.

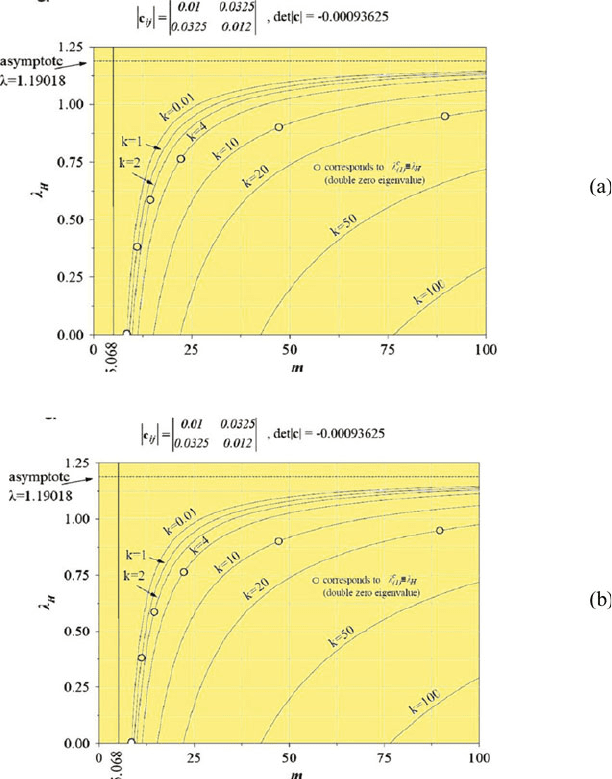
Fig.4a shows the generic Hopf bifurcation load λ

versus mass ratio

m(= m

)>5.068 for various values of stiffness ratio k(= k

). The small circle

in each k-curve corresponds to the critical divergence or static (buckling) load

(≡λ

). This corresponds to a dynamic bifurcation associated with a coupled

divergence–flutter instability (Fig.1d). This double zero eigenvalue dynamic bi-

furcation is called an Arnold–Bogdanof dynamic bifurcation [4]. Below the small

circle we have λ

for each value of k. Clearly, both

and λ

increase with

the increase of k. Fig.4b shows a generic Hopf bifurcations load λ

versus mass

ratio m(= m

)<5.068 for various stiffness ratios k(= k

). The values of λ

are

higher than λ = 1.19018 (asymptote). It is worth noticing that a discontinuity in the

flutter load versus mass was first observed in a continuous damped cantilever

model carrying concentrated (attached) masses [22, 23].

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 107

Fig. 4. Hopf bifurcation load λ

versus mass ratio m(=m

) for various values of stiffness

ratios k(=k

) : (a) for m>5.068; (b) for m<5.068.

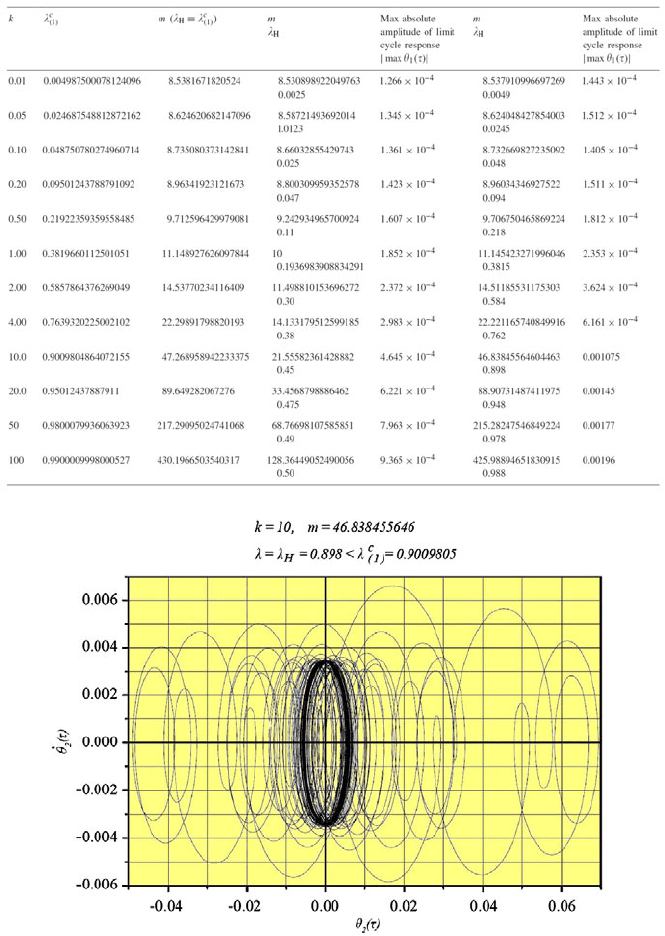
108 A.N. Kounadis

Table 1. Buckling and flutter loads

and λ

as well as |maxθ(τ)| for various stiffness

and mass ratios k and m

Fig. 5. Phase-plane portrait of the Hopf bifurcation of a 2-DOF model with k=10 and

m=46.838455646.