Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Directional Distortional Hardening in Plasticity within Thermodynamics 69

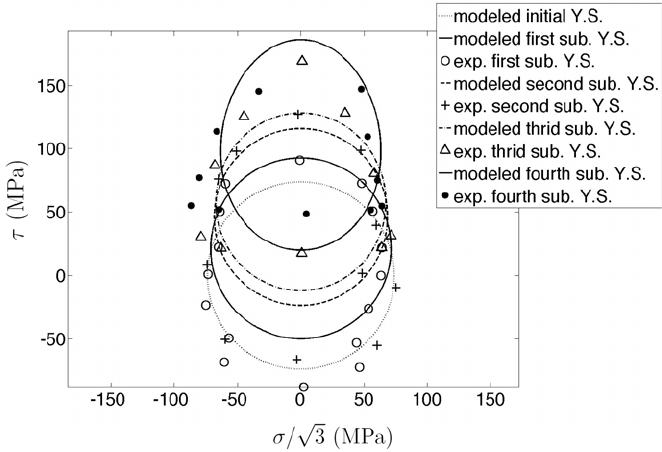
Fig. 3. α

α-model with evolving c compared to torsion experiments by Wu and Yeh (1991).

The ﬁrst, second, third, and fourth subsequent yield surfaces resulted from strain controlled

loading with ﬁnal values γ = 0.19%,0.38%,0.49% and 1.03%, respectively. Lines represent

the proposed constitutive model and discrete points represent experimental data.

models can simulate complex loading paths. The ﬁtting of the data in Fig. 9 may be

considered satisfactory given the simplicity of the model used, however, as Fig. 8

shows the A

A-model simulates the data better.

3.1 Ratchetting

Since the A

A-model is the most complete and ﬁts experimentally found yield surfaces

best, it will be used to simulate experimental cyclic plastic loading data. During

cyclic plastic loading, plastic strain accumulates and this is called ratchetting. When

the load is applied in two directions biaxial ratchetting occurs. Both stress and stress

controlled cyclic biaxial tests from Hassan et al. [9] will be simulated, and uniaxial

cyclic tests from Hassan and Kyriakides [8] will be used for calibration. In biaxial

stress controlled tests the material ratchets in two directions, and thus these test have

been especially difﬁcult to simulate.

Experiments in the study by Hassan and Kyriakides [8] and Hassan et al. [9] were

performed on thin walled tubes of carbon steel 1026. For the uniaxial experiments,

axial stress was applied cyclically. Various levels of mean stress σ

were used and

the stress amplitude was σ

= 0.79σ

,whereσ

= 40 ksi. For the strain controlled

biaxial data, the tubes were ﬁrst loaded with internal pressure σ

and then cycled

axially using various levels of strain amplitude ε

. While the cyclic loading was

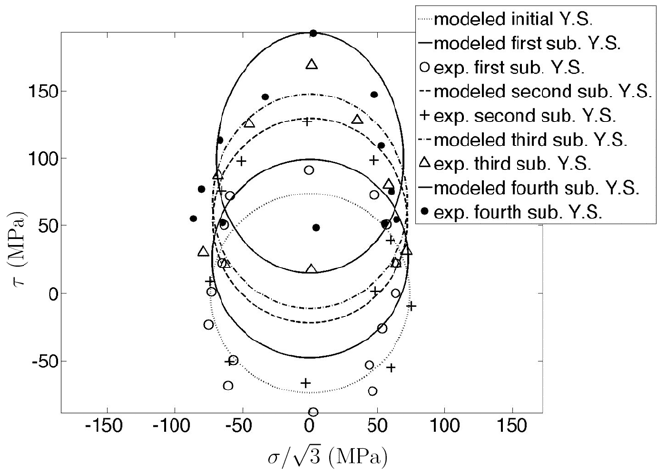
70 Y.F. Dafalias and H.P. Feigenbaum

Fig. 4. r-model compared to torsion experiments by Wu and Yeh (1991). The ﬁrst, second,

third, and fourth subsequent yield surfaces resulted from strain controlled loading with ﬁ-

nal values γ = 0.19%,0.38%,0.49% and 1.03%, respectively. Lines represent the proposed

constitutive model and discrete points represent experimental data.

occurring the internal pressure was kept constant. This results in strain accumula-

tion, i.e., ratchetting, in the circumferential direction ε

. For the stress controlled

biaxial data, tubes were ﬁrst stabilized by strain symmetric axial cycles in the range

of ±1% and in approximately twelve cycles the hysteresis loops were stable. Fol-

lowing the strain symmetric cycling the specimens were unloaded to approximately

zero axial stress and strain, although typically some small residual circumferential

strain remained non-zero, then preloaded using stress control with various internal

pressures. Following the internal pressure, the tubes were stress controlled cyclically

loaded in the axial direction about a nonzero mean stress σ

with amplitude σ

The stress controlled biaxial loading in conjunction with the cycling about nonzero

mean axial stress results in plastic strains accumulating in both the circumferential

and the axial directions.

With kinematic hardening alone, the Armstrong-Frederick kinematic hardening

rule generally does not ﬁt experimental results from cyclic plastic loading paths

very well, therefore researchers have developed numerous other kinematic harden-

ing rules which show improvement in ﬁtting cyclic loading. This paper will use the

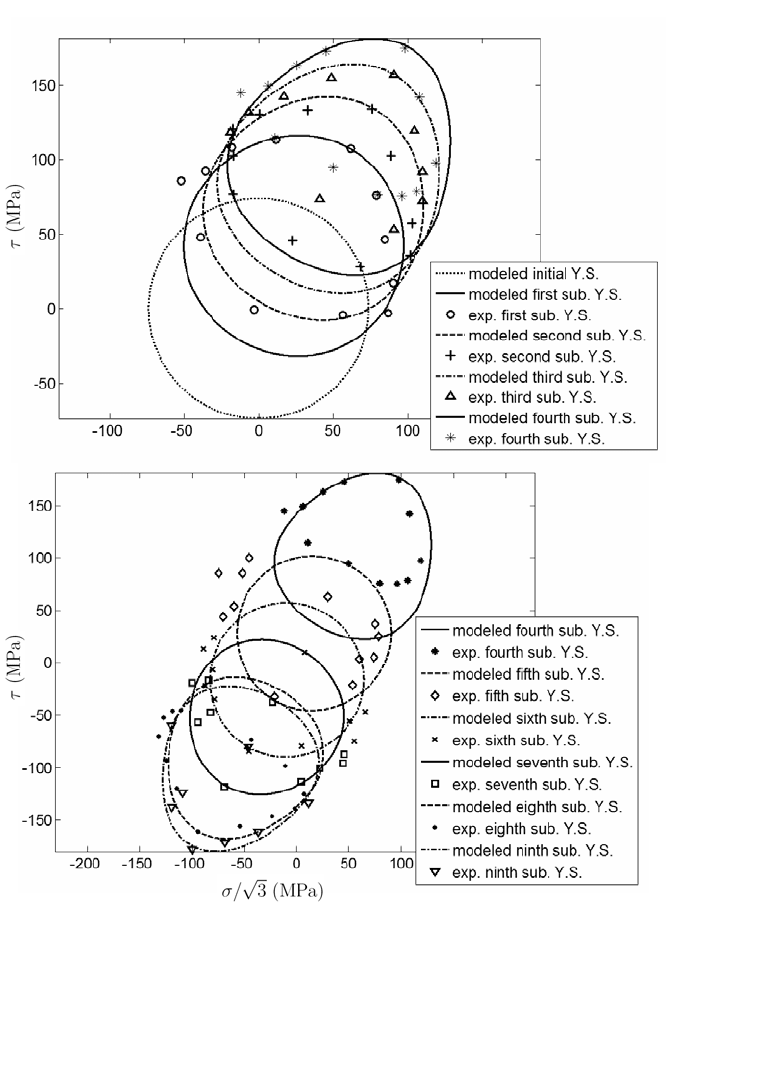
Directional Distortional Hardening in Plasticity within Thermodynamics 71

Fig. 5. A

A-model compared to stress controlled combined tension-torsion experiments by Wu

and Yeh [18]. Top ﬁgure shows the loading and bottom ﬁgure shows unloading and nega-

tive loading. For both ﬁgures the loading path was proportional with normal stress equal to

shear stress, i.e., σ = τ. Lines represent the proposed constitutive model and discrete points

represent experimental data.

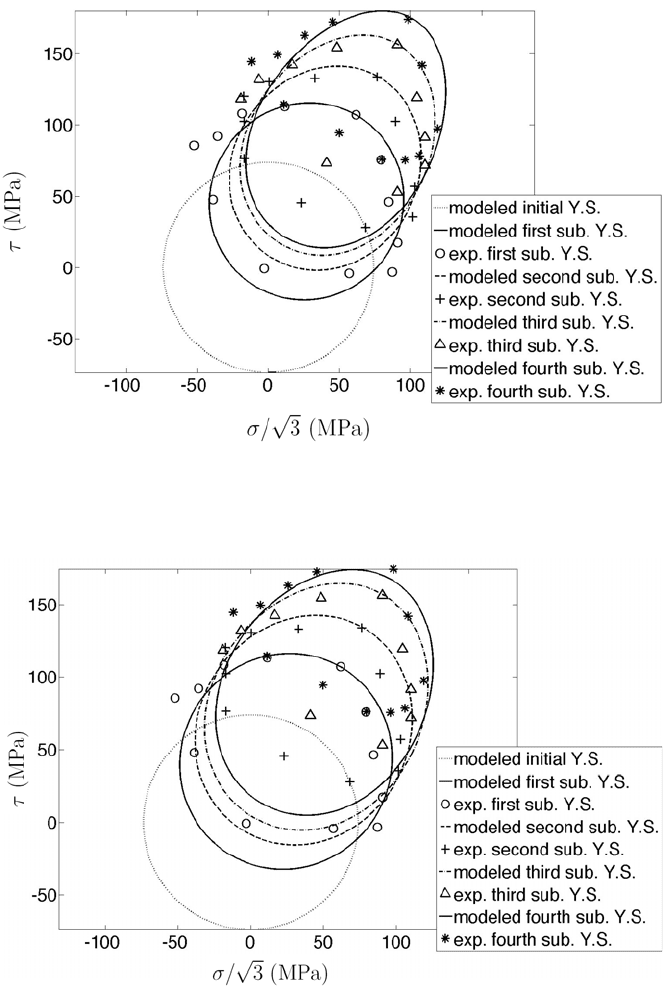
72 Y.F. Dafalias and H.P. Feigenbaum

Fig. 6. α

α-model with evolving c compared to stress controlled combined tension-torsion ex-

periments by Wu and Yeh (1991). The loading path was proportional with normal stress equal

to shear stress, i.e., σ = τ. Lines represent the proposed constitutive model and discrete points

represent experimental data.

Fig. 7. r-model compared to stress controlled combined tension-torsion experiments by Wu

and Yeh (1991). The loading path was proportional with normal stress equal to shear stress,

i.e., σ = τ. Lines represent the proposed constitutive model and discrete points represent

experimental data.

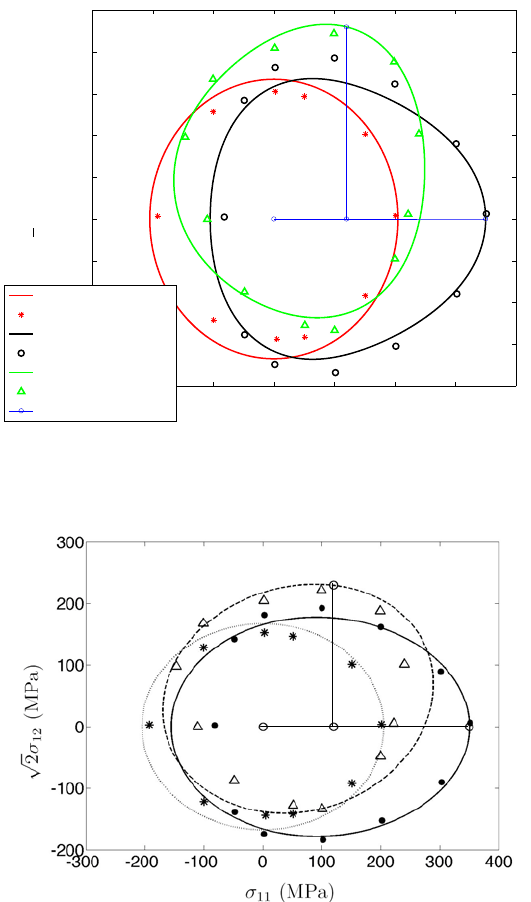
Directional Distortional Hardening in Plasticity within Thermodynamics 73

−300 −200 −100 0 100 200 300 400

−200

−150

−100

−50

100

150

200

250

(MPa)

√

2σ

(MPa)

Comp. initial YS

Exp. initial YS

Comp. 1st sub. YS

Exp. 1st sub. YS

Comp. 2nd sub. YS

Exp. 2nd sub. YS

Load path O−A−B−C

Fig. 8. A

A-model compared to stress controlled combined tension and shear experiments by

Boucher et al. [3]. Specimens were loaded in pure tension, unloaded some, then loaded in

pure torsion. The load path is shown on the ﬁgure as O-A-B-C.

OAB

Fig. 9. α

α-model with ﬁxed c compared to stress controlled combined tension and shear ex-

periments by Boucher et al. [3]. Specimens were loaded in pure tension, unloaded some, then

loaded in pure torsion. The load path is shown on the ﬁgure as O-A-B-C. Computed initial

yield surface: ···, experiential initial yield points: ∗, computed ﬁrst subsequent yield surface:

—–, experiential ﬁrst subsequent yield points: •, computed second subsequent yield surface:

---, experiential second subsequent yield points: .

74 Y.F. Dafalias and H.P. Feigenbaum

Table 2. Material constants used to ﬁt ratchetting data from Hassan et al. [9].

without distortion with distortion

18.8 18.8

20000 19000

32.85

400 380

8.07 7.67

10.45 11

39.3 41.36

5000 5000

a 55

-2

- 1125

kinematic hardening rule proposed by Chaboche [4] for cyclic loading. This kine-

matic hardening rule can be expressed as:

α =



i=1

= λ



∂f

∂σ





(



n− α

)(i = 1, 2, 3)

= λ



∂f

∂σ









n − α



1 −

f(α

)





(19)

where f(α

α)=



α : α

α.

To calibrate the model for ratchetting data, the model with kinematic harden-

ing alone was calibrated by Bari and Hassan [2] and then both material parameters

associated rate and saturation values for kinematic hardening are decreased and di-

rection distortional hardening parameters are added using Eqns. (17) and (18) as a

guide. This procedure exactly mimics what was done to ﬁt experimentally found

yield surfaces, except in this case the strain symmetrically stabilized data as well as

the uniaxial cyclic data were used for calibration. For simplicity no isotropic harden-

ing was included and no adjustments were made to the parameters associated with

, where the threshold is contained, and approximately equal adjustments were

made to the parameters associated with α

where i =1, 2, or 3. The results of the

calibration can be seen in Fig. 10 and the parameters are given in Table 2 where all

units are consistent with ksi.

Figs. 11 and 12 show the model simulating ratchetting data from Hassan et al. [9].

For the strain controlled ratchetting in Fig. 11 the model with directional distortional

hardening performs about as well as the model with kinematic hardening alone. For

the stress controlled ratchatting in Fig. 12, the model with directional disortional

Directional Distortional Hardening in Plasticity within Thermodynamics 75

0 10 20 30 40 50

0.5

1.5

2.5

3.5

4.5

θ p

(%)

= 0.79 σ

= 0.225 σ

= 0.160 σ

= 0.104 σ

Fig. 10. A

A-model as calibrated to the uniaxial ratchetting experimental data. The simulations

with kinematic hardening alone are shown as solid lines, the simulation with kinematic hard-

ening and directional distortional hardening are shown as dashed lines, and the experimental

data are shown as discrete points. In all cases the stress amplitude is σ

= 0.79σ

and three

different mean stress σ

values are shown.

0 5 10 15 20 25 30

0.5

1.5

2.5

3.5

θ p

(%)

= 0.24 σ

= 0.4%

= 0.65%

= 0.5%

= 0.65%

= 0.5%

Fig. 11. Strain controlled biaxial ratchetting simulations and experimental data. The simula-

tions with kinematic hardening alone are shown as solid lines, the simulation with kinematic

hardening and directional distortional hardening are shown as dashed lines, and the experi-

mental data are shown as discrete points. In all cases the internal pressure is kept constant

(σ

= 0.24σ

) while the strain is cycled symmetrically at different amplitude, ε

76 Y.F. Dafalias and H.P. Feigenbaum

−1.5 −1 −0.5 0 0.5 1 1.5

−0.5

0.5

1.5

2.5

3.5

θ m

(%)

x m

(%)

= 0.353 σ

= 0.249 σ

= 0.120σ

= 0.8 σ

= 0.13 σ

max

= 45

(a)

−1 −0.5 0 0.5

−0.5

0.5

1.5

2.5

θ m

(%)

x m

(%)

= 0.318 σ

= 0.210 σ

(b)

Fig. 12. Stress controlled biaxial ratchetting simulations and experimental data. The simu-

lations with kinematic hardening alone are shown as solid lines, the simulation with kine-

matic hardening and directional distortional hardening are shown as dashed lines, and the

experimental data are shown as discrete points. The mean axial strain ε

and the mean

circumferential strain ε

θm

per cycle are both predicted values. In both 12(a) and 12(b) the

axial stress amplitude is σ

= 0.8σ

, the mean axial stress is σ

= 0.13σ

and 45 cycles

were performed. Each data set has a different the value for the internal pressure (which leads

to σ

Directional Distortional Hardening in Plasticity within Thermodynamics 77

hardening performs consistently better. For some data sets the addition of directional

distortion hardening results in more dramatic improvement (e.g., Fig. 12(b) with

= 0.210σ

), while in others the improvement is minor (e.g., Fig. 12(a) with

= 0.353σ

). Nonetheless, from Fig. 12 it is clear that directional distortional

hardening improves the simulation of stress controlled biaxial ratchetting.

4Conclusion

It is very importance to accurately model the shape of the yield surface when using

the associative ﬂow rule not only for capturing accurately the yield point, but mainly

because any deviation in shape may result in signiﬁcant deviation of the direction

of the normal to the yield surface and, thus, of the coaxial plastic strain increment,

which during cyclic loading and resulting ratcheting accumulates the error to unac-

ceptable levels. Three different models were developed within thermodynamics by

Feigenbaum and Dafalias [5, 6] capturing this phenomenon of directional distortion

of the yield surface, and for the ﬁrst time are presented in unison in this paper. The

Feigenbaum and Dafalias model [5] (i.e., the A

A-model) uses a fourth order tensor

and a scalar multiplier to capture directional distortion, and is the most successful

in data ﬁtting, albeit the most complex as well, of the three models. In particular

this model is used to simulate experimental data from biaxial cyclic loading test

showing the improvement of simulations for ratchetting obtained by the introduced

directional distortional hardening scheme as compared with simulations which do

not involve directional distortion of the yield surface.

References

[1] Bardet, J.P., Choucair, W.: A linearized integration technique for incremental constitu-

tive equations. International Journal for Numerical and Analytical Methods in Geome-

chanics 15, 1–19 (1991)

[2] Bari, S., Hassan, T.: Anatomy of coupled consititutive models for ratcheting simulation.

International Journal of Plasticity 16, 381–409 (2000)

[3] Boucher, M., Cayla, P., Cordebois, J.P.: Experimental studies of yield surfaces of alu-

minum alloy and low carbon steel under complex biaxial loadings. European Journal of

Mechanics, A/Solids 14(1), 1–17 (1995)

[4] Chaboche, J.L.: On some modiﬁcations of kinematic hardening to improve the descrip-

tion of ratcheting effects. International Journal of Plasticity 7, 661–678 (1991)

[5] Feigenbaum, H.P., Dafalias, Y.F.: Directional distortional hardening in metal plasticity

within thermodynamics. International Journal of Solids and Structures 44, 7526–7542

(2007)

[6] Feigenbaum, H.P., Dafalias, Y.F.: Simple model for directional distortional hardening

in metal plasticity within thermodynamics. ASCE Journal of Engineering Mechan-

ics 134(9), 730–738 (2008)

[7] Franc¸ois, M.: A plasticity model with yield surface distortion for non proportional load-

ing. International Journal of Plasticity 17, 703–717 (2001)

[8] Hassan, T., Kyriakides, S.: Ratcheting in cyclic plasicity, part i: Uniaxial behavior. In-

ternational Journal of Plasticity 8, 91–116 (1992)

78 Y.F. Dafalias and H.P. Feigenbaum

[9] Hassan, T., Corona, E., Kyriakides, S.: Ratcheting in cyclic plasicity, part ii: Multiaxial

behavior. International Journal of Plasticity 8, 117–146 (1992)

[10] Kurtyka, T., Zyczkowski, M.: Evolution equations for distortional plastic hardening.

International Journal of Plasticity 12(2), 191–203 (1996)

[11] McComb, H.G.: Some experiments concerning subsequent yield surfaces in plasticity.

Tech. Rep. D-396, National Aeronautics and Space Adminstration (1960)

[12] Naghdi, P.M., Essenburg, F., Koff, W.: An experimental study of initial and subsequent

yield surfaces in plasticity. Journal of Applied Mechanics 25(2), 201–209 (1958)

[13] Ortiz, M., Popov, E.P.: Distortional hardening rules for metal plasticity. Journal of En-

gineering Mechanics 109(4), 1042–1057 (1983)

[14] Phillips, A., Tang, J.L., Ricciuti, M.: Some new observations on yield surfaces. Acta

Mechanica 20, 23–39 (1975)

[15] Plesek, J., Feigenbaum, H.P., Dafalias, Y.F.: Convexity of yield surfaces with direc-

tional distortional hardening. ASCE Journal of Engineering Mechanics 136(4), 477–

484 (2010)

[16] Voyiadjis, G.Z., Foroozesh, M.: Anisotropic distortional yield model. Journal of Ap-

plied Mechanics 57, 537–547 (1990)

[17] Wei-Ching Yeh, C.D.H., Pan, W.F.: An endochronic theory accounting for deforma-

tion induced anisotropy of metals under biaxial load. International Journal of Plastic-

ity 12(8), 987–1004 (1996)

[18] Wu, H.C., Yeh, W.C.: On the experimental determination of yield surfaces and some

results of annealed 304 stainless steel. International Journal of Plasticity 7, 803–826

(1991)