Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics
Подождите немного. Документ загружается.


Scaling of Strength and Lifetime Distributions of Quasibrittle Structures 49
= n
b
!S
p
1
+p
2
+...+p
n
b
Ω
n
b
(1)
n
b
∏
i=1
p
i
y
p
i
−1
i
s
p
i
0
dy
1
dy
2
...dy
n
b
(9)
where
Ω
n
b
(S) is the feasible region of stresses in all the fibers, which defines an n
b
-
dimensional space, and
Ω
n
b
(1) is the corresponding feasible region of normalized
stresses, y
i
=
σ
i
/S.
Thus, regardless of the post-peak slope E
t
of each fiber, it is proven that, if each
fiber strength has a cdf with a power-law tail, then the cdf of bundle strength will also
have a power-law tail, and the power-law exponent will be the sum of the exponents
of the power-law tails of the cdf’s of all the fibers in the bundle.
The reach of power-law tail of the strength cdf of softening bundle was shown to
be another important consideration [13]. It can be calculated from Eq. 9. However,
for large bundles, it is difficult to handle the integral in Eq. 9 numerically. Previous
studies [12, 13] showed that the reach of power-law tail decreases with the num-
ber n
b
of elements rapidly as P
tn
b
∼ (P
t1
/n
b
)
n
b
−(P
t1
/3n
b
)
n
b
for brittle bundles, or
(P
t1
/n
b
)
n
b
for plastic bundles, where P
t1
= failure probability at the terminal point of
the power-law tail of one fiber. Since the behavior of softening bundles is bounded
between these two extreme cases, the rate of shortening of power-law tail of strength
cdf of the softening bundles must lie between them; i.e.
P
tn
b
∼ (P
t1
/n
b
)
n
b
−(P
t1
/3n
b
)
n
b
(10)
The series coupling, by contrast, was shown to extend the power-law tail [13]—
roughly by one order of magnitude for each ten-fold increase in the number links.
Another important asymptotic property is the type of cdf of strength of large bun-
dles. For brittle bundles, Daniels derived a recursive equation for the strength cdf of
a bundle with n
b
fibers and showed that the strength cdf of large bundles approaches
the Gaussian (or normal) distribution [20]. This property is obviously also true for
plastic bundles; it is a natural consequence of the Central Limit Theorem since the
strength of a plastic bundle is the sum of strengths of all the fibers.
To prove that this asymptotic property applies to all the bundles regardless of
their post-peak softening stiffness E
t
, consider a bundle of 3n
b
fibers (or elements).
The load carried by the bundle is given by F(
ε
)=max
∑
3n
b
+1
j=2
σ
j
(
ε
)A
,where
A = cross section area of each fiber,
σ
j
= stress in jth element, and
ε
= strain in
each element. The mechanical behavior of each fiber can be random. This causes
the randomness of the critical value
ε
∗
of strain
ε
,atwhichF reaches its maximum
value. We label the 3n
b
elements by j = 2, 3,4, ...3n
b
+1, arrange them according to
their breaking order, and divide them into two groups with different load resultants:
F
A
(
ε
)=
∑
i=3k
σ
i
(
ε
)A, F
B
(
ε
)=
∑
i=3k±1
σ
i
(
ε
)A (k = 1,2,3,...n
b
). (11)
The maximum load carried by the bundle is:
F
max
= F
A
(
ε
∗
)+F
B
(
ε
∗
) (12)
50 Z.P. Baˇzant and J.-L. Le
2
3n
b
+1
…
3
Stress distribution in the bundle
3
24
6
9
5
12
…
3
…
24
Stress distribution in
sub
bundle
B
Stress distribution in
sub
bundle
A
6
9
5
12
sub
-
bundle
B
sub
-
bundle
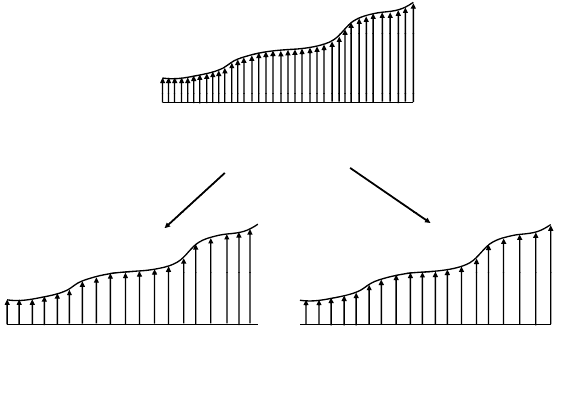
A
Fig. 3. Stress distribution of fibers within a large bundle.
If n is large, then the stress distribution over the elements in these two groups will be
similar to that in the bundle (Fig. 3). It follows that the cdf of F
max
(i.e. the strength
of bundle) and the cdf’s of F
A
(
ε
∗
) and F
B
(
ε
∗
) are of the same type. Then, to satisfy
Eq. 12, the only possible distribution of F
max
is the Gaussian distribution (note that
this argument would not apply if the we divided the bundle into 2 groups with the
same number of elements and the same resultant for large n
b
).
However, the rate of convergence depends on the post-peak softening stiffness E
t
of the elements. The slowest convergence, of the order of O(n
b
−1/3
(logn
b
)
2
) [48],
occurs for brittle bundles. The fastest convergence, of the order of O(n
b
−1/2
), occurs
for plastic bundles [13].
To figure out the type of cdf of strength of one RVE, one must specify the me-
chanical behavior of the bundles in the hierarchical model. Although different as-
sumptions yield about the same results, here the following assumption is made: For
the bundles at the lowest scale, the elements are connected between two rigid plates,
and thus they are subjected to the same deformation. For the bundles at higher scales,
they follow the equal-load sharing mechanism.
Note that one should calculate the strength cdf in a hierarchical manner, at the
lowest scale, each element represents a nano-structure whose strength cdf is a power-
law function. One can then calculate the strength cdf of the sub-chain that connects
these elements. At the next scale, the strength cdf of the sub-bundle, which consists
of these sub-chains, can be calculated based on the strength cdf of these sub-chains.
Following in this manner, one could move up through the scales, and finally obtain
the strength cdf of one RVE.

Scaling of Strength and Lifetime Distributions of Quasibrittle Structures 51
The strength cdf of all the sub-chains follows from the joint probability theorem.
For the bundles at the lowest scale, where all the elements are subjected to a roughly
uniform deformation, the strength cdf will depend on the mechanical behavior of
each element, which is given by Eq. 8, and for the bundles at higher scales, equal-
load sharing is assumed. Regardless of the mechanical behavior of each element,
the strength of a bundle with the equal-load sharing mechanism is given by:
σ
b
= max
σ
1
,
n
b
−1
n
b
σ
2
,...,
1
n
b
σ
n
b
(13)
where
σ
1
,
σ
2
,...
σ
n
b
are the strength values ordered by the sequence of their break-
ing. In fact, the strength distribution of such a bundle is exactly the same as the
strength distribution of the brittle bundle. Therefore, the strength distribution of
the equal-load sharing bundle can be calculated by Daniels’ recursive equation
[20, 28, 13].
As an example, we calculate the strength cdf of the hierarchical model shown in
Fig. 1. Every element in the hierarchical model represents one nanoscale element,
which has a power-law cdf of strength. Three cases are considered:
1) Each element has an elastic-brittle behavior.
2) Each element exhibits a linear post-peak softening, where the softening
modulus magnitude is 40% of the elastic modulus of the element.
3) Each element has an elastic-plastic behavior.
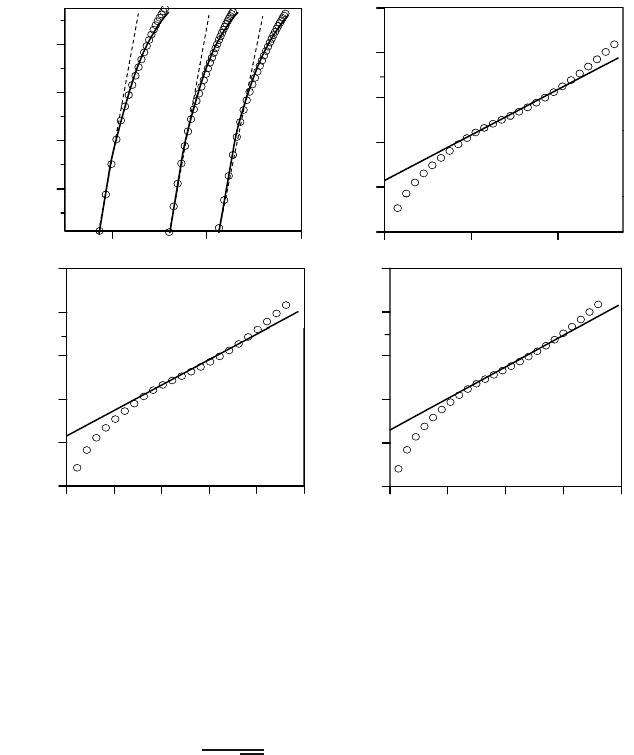
Fig. 4a shows the calculated strength cdf’s of the hierarchical model for these three
cases on the Weibull scale. For all these cases, the lower portion of the calculated
strength cdf is a straight line on the Weibull plot, which indicates that it follows the
Weibull distribution (a power-law tail). Such a property is expected since the power-
law tail of the cdf of strength is indestructible in the chain and bundle models.
For the upper portion, the strength cdf deviates from the straight line in Fig. 4a.
Among the three cases considered, case 1 (i.e., elements with brittle behavior) gives
the shortest Weibull tail, which terminates at the probability of about 0.7 ×10
−4
,
while case 3 (elements with plastic behavior) gives the longest Weibull tail, which
terminates at the probability of about 0.7 ×10
−3
.
To identify the type of distribution for the upper portion of the cdf, the cdf’s
of strengths are plotted on the normal probability paper; see Figs. 4b-d where the
upper portion of the cdf’s is seen to be fitted quite closely by a straight line. The
straight line not is not too close for case 1 and for P
f
≥ 0.8. For the cases 2 and 3,
the straight line fits quite closely, with a slight deviation occurring only for P
f
≥
0.99. This means that, the upper portion of the strength cdf can be approximated as
the Gaussian distribution. Since, for real quasibrittle structures, the nano-element is
expected to have a softening behavior, the strength cdf of one RVE should be close
to case 2.
In general, the strength distribution of one RVE can be approximately described
by a Gaussian distribution with a Weibull tail grafted on the left at the probability of
52 Z.P. Baˇzant and J.-L. Le
0
0.999968
P
f
)
]}
a)
b)
-4
0.5
0.9772
/(1
P
f
)
-12
-8
6.22u10
-16
3.16u10
-5
ln{ln[1
Brittle
Softening
-4 -2 0
00.020.04
Brittle
1.77u10
-33
ln
V
V
Softening
Plastic
0.999968
P
f
0.999968
P
f
c)
d)
316
10
5
0.5
0.9772
0.5
0.9772
Sft i
6.22u10
-16
3
.
16
u
10
-
5
6.22u10
-16
3.16u10
-5
0 0.05 0.1 0.15 0.2 0.25
0 0.2 0.4 0.6 0.8
S
o
ft
en
i
ng
Plastic
1.77u10
-33
1.77u10
-33
V
V
Fig. 4. a) Calculated cdf of strength of one RVE on the Weibull scale, b)–d) Calculated cdf
of strength of one RVE on the normal distribution paper.
about 10
−4
−10
−3
. The grafted cdf of strength of one RVE may be mathematically
described as [12, 13]:
P
1
(
σ
N
)=1 − e
−(
σ
N
/s
0
)
m
(
σ
N
≤
σ
gr
) (14)
P
1
(
σ
N
)=P
gr
+
r
f
δ
G
√
2
π
σ
N
σ
gr
e
−(
σ
−
μ
G
)
2
/2
δ
2
G
d
σ
(
σ
N
>
σ
gr
) (15)
where
σ
N
= nominal strength, which is a maximum load parameter of the dimension
of stress. In general,
σ
N
= c
n
P
max
/bD or c
n
P
max
/D
2
for two- or three-dimensional
scaling (P
max
= maximum load of the structure or parameter of load system, c
n
=
parameter chosen such that
σ
N
represents the maximum principal stress in the struc-
ture, b = structure thickness in the third dimension, D = characteristic structure di-
mension or size). Furthermore, m (Weibull modulus) and s
0
are the shape and scale
parameters of the Weibull tail, and
μ
G
and
δ
G
are the mean and standard deviation of
the Gaussian core if considered extended to −∞; r
f
is a scaling parameter required
to normalize the grafted cdf such that P
1
(∞)=1, and P
gr
= grafting probability =
1 −exp[−(
σ
gr
/s
0
)
m
]. Finally, continuity of the probability density function at the
grafting point requires that (dP
1
/d
σ
N
)|
σ
+
gr
=(dP
1
/d
σ
N
)|
σ
−
gr
.

Scaling of Strength and Lifetime Distributions of Quasibrittle Structures 53
4 Lifetime Distribution of One RVE
It has recently been shown [8, 33, 5] that one can derive the lifetime cdf of one
RVE by using the power law for creep crack growth, which has been empirically
described as [23, 51, 24, 15, 14, 4, 37]:
˙a = Ce
−Q
0
/kT
K
n
(16)
where C,n = empirical constant, Q
0
= activation energy, k = Boltzmann’s constant,
T = absolute temperature, K = stress intensity factor. Recent studies [8, 33] showed
that, under certain plausible assumptions, the power law for creep crack growth can
be physically justified on the basis of atomistic fracture mechanics and a multi-scale
transition framework of fracture kinetics.
Now consider one RVE undergoing strength and lifetime tests, where a linearly
ramped load is applied in the strength test and a constant load is applied in the
lifetime test. By applying Eq. 16 to these two cases, one finds the relation between
the strength and lifetime of one RVE as:
σ
N
=
βσ
n/(n+1)
0
λ
1/(n+1)
(17)
where
σ
N
= nominal strength of RVE,
σ
0
= P/l
0
2
= applied nominal stress in the
lifetime test (P = applied load), l
0
= RVE size,
λ
= lifetime of RVE,
β
=[r(n +
1)]
1/(n+1)
,andr = rate of loading in the strength test. Since the distribution of RVE
strength is given by Eqs. 14 and 15, the lifetime distribution of one RVE can be
easily obtained by substituting Eq. 17 for
σ
N
of Eqs. 14 and 15:
for
λ
<
λ
gr
: P
1
(
λ
)=1 −exp[−(
λ
/s
λ
)
¯m
]; (18)
for
λ
≥
λ
gr
: P
1
(
λ
)=P
gr
+
r
f
δ
G
√
2
π
γλ
1/(n+1)
γλ
1/(n+1)
gr
e
−(
λ
−
μ
G
)
2
/2
δ
2
G
d
λ
(19)
where
γ
=
βσ
n/(n+1)
0
λ
gr
=
β
−(n+1)
σ
−n
0
σ
n+1
N,gr
, s
λ
= s
n+1
0
β
−(n+1)
σ
−n
0
,and ¯m =
m/(n + 1). Similar to the strength distribution of one RVE, the lifetime cdf of one
RVE also has a Weibull tail (power-law tail). However, the rest of the lifetime cdf
of one RVE does not follow the Gaussian distribution. Note that the grafting proba-
bility P
gr
for the lifetime distribution of one RVE is the same as that for the strength
cdfofoneRVE.
5 Finite Weakest Link Model and Optimum Fits of Histograms
To analyze softening damage and failure, the RVE must be defined as the smallest
material volume whose failure triggers the failure of entire structure [12, 13]. There-
fore, the structure can be statistically represented by a chain of RVEs. By virtue of
the joint probability theorem, and under the assumption of independence of random
strengths or lifetimes of the links in a finite weakest-link model, one can calculate
the strength or lifetime cdf of a structure as:
54 Z.P. Baˇzant and J.-L. Le
P
f
(x)=1 −
N
∏
i=1
[1 −P
1
(x)] (20)
where x =
σ
N
for strength distribution and x =
λ
for lifetime distribution, P
1
=
strength or lifetime cdf of one RVE given by Eqs. 14 and 15 or Eqs. 18 and 19.Here
we assume that the principal stresses in one RVE are fully statistically correlated to
the maximum one, which seems realistic. If they were uncorrelated, each principal
stress would require one element in the chain.
For large size structures, what matters for P
f
is only the tail of the strength or life-
time cdf of one RVE, i.e P
1
=(
σ
N
/s
0
)
m
or P
1
=(
λ
/s
λ
)
¯m
. By taking the logarithm
of Eq. 20 and setting ln(1 −P
1
) ≈−P
1
for small P
1
, one can easily show that the
strength and lifetime distributions for large size structure converge to the Weibull
distribution:
P
f
(
σ
N
)=1 −exp[−N
eq,
σ
(
σ
/s
0
)
m
] (21)
P
f
(
λ
)=1 −exp[−N
eq,
λ
(
λ
/s
λ
)
¯m
] (22)
where N
eq,
σ
,N
eq,
λ
are the equivalent numbers of RVEs for the strength and lifetime
distributions, which can be calculated based on the elastic stress distribution in the
structure [13, 5]. The equivalent number of RVE physically means that a chain that
has N
eq,
σ
or N
eq,
λ
RVEs subjected to a uniform stress gives the same strength or
lifetime cdf as Eq. 20. The Weibull modulus of lifetime distribution is much smaller
than the Weibull modulus of strength distribution. They are related by:
¯m = m/(n + 1) (23)
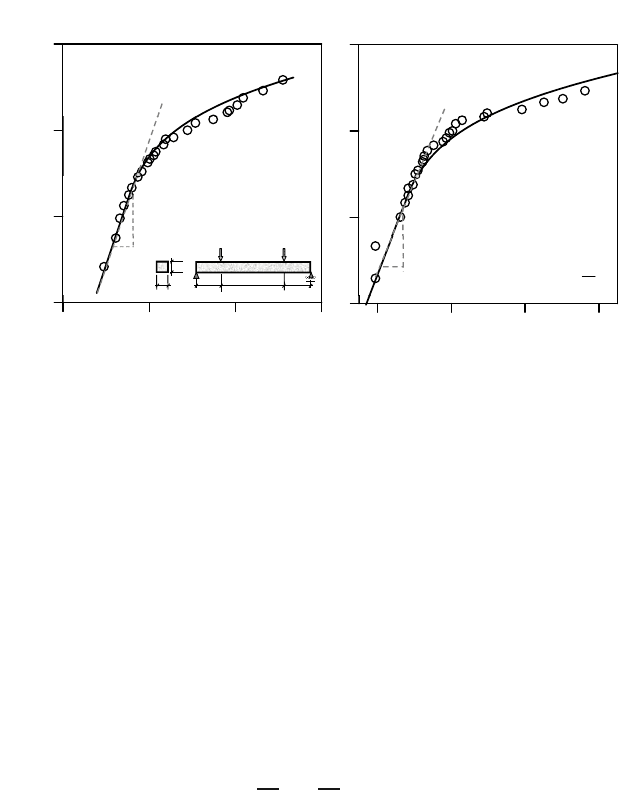
Fig. 5 presents the optimum fits of the strength and lifetime histograms of 99.9
%Al
2
O
3
beam under four point bend test [25]. For each histogram, a total of 30
specimens were tested. Obviously, on the Weibull scale, both histograms do not
appear to be straight lines. Instead, there is a kink separating the histogram into two
parts where the lower part is a straight line and the upper part is curved. Such a
pattern cannot be explained by the two-parameter Weibull distribution.
Fig. 5 shows that the present theory gives excellent fits of both the strength and
lifetime histograms. The location of kink actually corresponds to the grafting prob-
ability, which measures the degree of quasibrittleness of the structure.
From the data fits, it is further observed that the grafting probabilities of the
strength and lifetime cdf’s are about the same. This agrees well with the present
theory, in which the grafting probability can be calculated as: P
gr
= 1−[1−P
gr,1
]
N
eq
.
Since the grafting probabilities P
gr,1
of strength and lifetime cdf’s for one RVE is
the same and the equivalent number of RVE for strength cdf is almost identical to
the equivalent number of RVE for lifetime cdf, then the grafting probabilities for
strength and lifetime cdf’s must be approximately the same.
By optimum fitting, the Weibull moduli for strength and lifetime distributions are
estimated to be about 30 and 1.1, respectively. From Eq. 23 one can get exponent n
of the power law for creep crack growth for 99.9 % Al
2
O
3
, which is about 26.
Scaling of Strength and Lifetime Distributions of Quasibrittle Structures 55
2
99 6% Al
O
2
99 6% Al
O
Strength Distribution Lifetime Distribution
P
f
)]}
99
.
6%
Al
2
O
3
99
.
6%
Al
2
O
3
/
(1
P
0
0
{
ln[1
/
-2
-2
30
11
ln
{
45
3.5
20
12 5
12 5
1
1
.
1
1
Constant load
N
VV
78.0
ln
V
ln
O
5.2 5.4 5.6 5.8
-4
4
.
5
20
12
.
5
12
.
5
-8 -4 0 4
-4
ln
V
N
ln
O
Fig. 5. Optimum fits of strength and lifetime histograms of 99.9 % Al
2
O
3
[25].
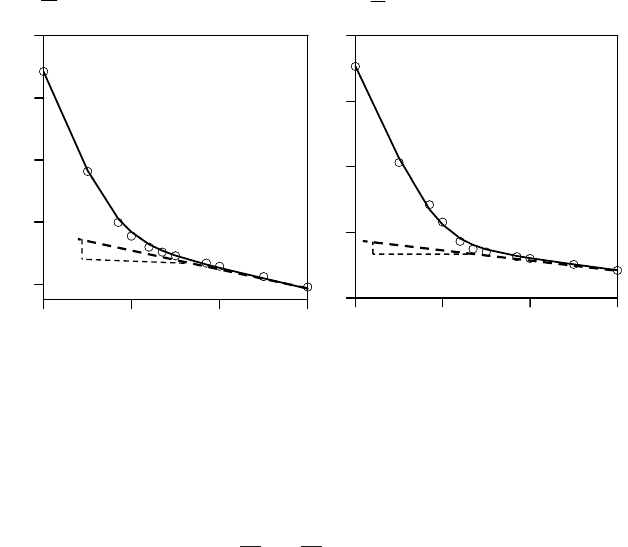
6 Size Effect on Mean Structural Strength and Lifetime
With the grafting probability distributions of strength and lifetime of one RVE, Eq.
20 directly implies the size effects on the strength and lifetime cdf’s. One can further
compute the size effects on the mean strength and lifetime. Based on the calibrated
strength and lifetime distributions of 99.9 % Al
2
O
3
(Fig. 5), one can calculate the
corresponding size effects on the mean structural strength and lifetime as shown in
Fig. 6.
Although a close-form expression for such size effects is impossible, one can ob-
tain the approximate form for the mean strength and lifetime by asymptotic match-
ing. It has been proposed that the size effect on mean strength can be approximated
by[2,3,11]:
¯
σ
N
=
N
a
D
+
N
b
D
ψ
/m
1/
ψ
(24)
where parameters N
a
, N
b
,
ψ
and m are to be determined by asymptotic properties of
the size effect curve.
It has been shown that such a size effect curve agrees well with the predictions
by other mechanical models such as the nonlocal Weibull theory [9, 10], as well
as with the experimental observations on concrete [16] and fiber composites [18];
m = Weibull modulus of the strength distribution, which can be determined by the
slope of the left tail of the strength histogram plotted on the Weibull scale, or more
accurately by size effect tests. The other three parameters, N
a
, N
b
,andr, can be
determined by solving three simultaneous equations based on three asymptotic con-
ditions, [
¯
σ
N
]
D→l
0
, [d
¯
σ
N
/dD]
D→l
0
,and[
¯
σ
N
D
1/m
]
D→∞
.
56 Z.P. Baˇzant and J.-L. Le
0.6
30
V
l
n
O
ln
M
ean
St
rengt
h
M
ean L
if
et
i
me
0.4
20
0.2
10
0
0
99.6% Al
2
O
3
99.6% Al
2
O
3
-0.2
10
1
1.1
1
30
0246
0246
-
10
Dln
Dln
Fig. 6. Calculated size effects on mean structural strength and lifetime.
One can approximate the size effect on the mean structural lifetime by an equa-
tion with the same form as Eq. 24:
¯
λ
=
C
a
D
+
C
b
D
ϕ
/m
(n+1)/
ϕ
(25)
where m is the Weibull modulus of the cdf of strength, and n = exponent of the
power law for subcritical creep crack growth rate. Similar to the size effect on mean
strength, C
a
, C
b
,and
ϕ
can be obtained from three asymptotic conditions: [
¯
λ
]
D→l
0
,
[d
¯
λ
/dD]
D→l
0
,and[
¯
λ
D
(n+1)/m
]
D→∞
.
It is obvious that the size effect on the mean structural lifetime is much stronger
than that on the mean strength. This is physically plausible. Consider two geometri-
cally similar beams, with size ratio 1:8. Let the nominal strength of the small beam
be
ς
. Due to the size effect on the mean strength, the nominal strength of the large
beam is about
ς
/2. If one applied a nominal load
ς
/2 to both beams, the large beam
will fail within standard laboratory testing period (i.e. about 5 minutes) while the
small beam is expected to survive at that load for decades if not forever.
7Conclusion
The present theory shows that the types of strength and lifetime distributions depend
on the structure size and geometry. This has important implications for the safety
factors to be used in reliability assessment for the design of many engineering struc-
tures, such as large prestressed concrete bridges, large aircraft or ships made of fiber
composites, and various micro- and nano-electronic devices.
Scaling of Strength and Lifetime Distributions of Quasibrittle Structures 57
The present theory indicates that the safety factors guarding against the uncer-
tainties in strength and lifetime cannot be empirical, and cannot be constant. They
must be calculated as a function of the size, geometry of structures and environment.
Acknowledgement. The theoretical development was partially supported under
Grant CMS-0556323 to Northwestern University (NU) from the U.S. National Sci-
ence Foundation. The applications to concrete and composites were partially sup-
ported under a Grant to NU from the U.S. Department of Transportation through
the NU Infrastructure Technology Institute, and Grant N007613 to NU from
Boeing, Inc.
References
1. Basquin, O.H.: The Exponential Law of Endurance Tests. In: Proc. Amer. Soc.Testing
and Mater., ASTEA, vol. 10, pp. 625–630 (1910)
2. Baˇzant, Z.P.: Scaling theory of quaisbrittle structural failure. Proc. Nat’l. Acad. Sci.,
USA 101(37), 13397–13399 (2004)
3. Baˇzant, Z.P.: Scaling of Structural Strength, 2nd edn. Elsevier, London (2005)
4. Baˇzant, Z.P., Jir´asek, M.: R-curve modeling of rate and size effects in quasibrittle frac-
ture. Int. J. of Frac. 62, 355–373 (1993)
5. Baˇzant, Z.P., Le, J.-L.: Nano-mechanics based modeling of lifetime distribution of qua-
sibrittle structures. J. Engrg. Failure Ana. 16, 2521–2529 (2009)
6. Baˇzant, Z.P., Le, J.-L.: Size effect on strength and lifetime distributions of quasibrittle
structures. In: Proc. (CD), ASME 2009 Int. Mech. Engrg. Congress (IMECE 2009), Lake
Buena Vista, Florida, pp. 1–9 (2009)
7. Baˇzant, Z.P., Le, J.-L., Bazant, M.Z.: Size effect on strength and lifetime distribution
of quasibrittle structures implied by interatomic bond break activation. In: Proc. of 17th
European Conference on Fracture, Brno, Czech Rep., pp. 78–92 (2008)
8. Baˇzant, Z.P., Le, J.-L., Bazant, M.Z.: Scaling of strength and lifetime distributions of
quasibrittle structures based on atomistic fracture mechanics. Proceeding of National
Academy of Sciences 106(28), 1484–11489 (2009)
9. Baˇzant, Z.P., Nov´ak, D.: Probabilistic nonlocal theory for quasibrittle fracture initiation
and size effect. I. Theory. J. of Engrg. Mech. 126(2), 166–174 (2000)
10. Baˇzant, Z.P., Nov´ak, D.: Probabilistic nonlocal theory for quasibrittle fracture initiation
and size effect. II. Application. J. of Engrg. Mech. ASCE 126(2), 175–185 (2000)
11. Baˇzant, Z.P., Nov´ak, D.: Energetic-statistical size effect in quasibrittle failure at crack
initiation. ACI Mater. J. 97(3), 381–392 (2000)
12. Baˇzant, Z.P., Pang, S.-D.: Mechanics based statistics of failure risk of quasibrittle
structures and size effect on safety factors. Proceeding of National Academy of Sci-
ences 103(25), 9434–9439 (2006)
13. Baˇzant, Z.P., Pang, S.-D.: Activation energy based extreme value statistics and size effect
in brittle and quasibrittle fracture. J. Mech. Phys. Solids 55, 91–134 (2007)
14. Baˇzant, Z.P., Planas, J.: Fracture and Size Effect in Concrete and Other Quasibrittle Ma-
terials. CRC Press, Boca Raton (1998)
15. Baˇzant, Z.P., Prat, P.C.: Effect of temperature and humidity on fracture energy of con-
crete. ACI Mater. J. 85-M32, 262–271 (1988)
16. Baˇzant, Z.P., Voˇrechovsk´y, M., Nov´ak, D.: Asymptotic prediction of energetic-statistical
size effect from deterministic finite element solutions. J. Engrg. Mech., ASCE 128, 153–
162 (2007)
58 Z.P. Baˇzant and J.-L. Le
17. Baˇzant, Z.P., Xi, Y.: Statistical size effect in quasi-brittle structures: II. Nonlocal theory.
J. Engrg. Mech., ASCE 117(7), 2623–2640 (1991)
18. Baˇzant, Z.P., Zhou, Y., Daniel, I.M., Caner, F.C., Yu, Q.: Size effect on strength of
laminate-foam sandwich plates. J. of Engrg. Materials and Technology ASME 128(3),
366–374 (2006)
19. Chiao, C.C., Sherry, R.J., Hetherington, N.W.: Experimental verification of an accel-
erated test for predicting the lifetime of oragnic fiber composites. J. Comp. Mater. 11,
79–91 (1977)
20. Daniels, H.E.: The statistical theory of the strength of bundles and threads. Proc. R. Soc.
London A. 183, 405–435 (1945)
21. Duckett, K.: Risk analysis and the acceptable probability of failure. The Structural Engi-
neering 83(15), 25–26 (2005)
22. Duffy, S.F., Powers, L.M., Starlinger, A.: Reliability analysis of structural ceramic com-
ponents using a three-parameter Weibull distribution. Tran. ASME J. Eng. Gas Turbines
Power 115, 109–116 (1993)
23. Evans, A.G.: A method for evaluating the time-dependent failure characteristics of brit-
tle materials and its application to polycrystalline alumina. J. Mater. Sci. 7, 1146–1173
(1972)
24. Evans, A.G., Fu, Y.: The mechanical behavior of alumina. In: Fracture in Ceramic Ma-
terials, pp. 56–88. Noyes Publications, Park Ridge (1984)
25. Fett, T., Munz, D.: Static and cyclic fatigue of ceramic materials. In: Vincenzini, P. (ed.)
Ceramics Today – Tomorrow’s Ceramics, pp. 1827–1835. Elsevier Science Publisher B.
V., Amsterdam (1991)
26. Graham-Brady, L.L., Arwadea, S.R., Corrb, D.J., Guti´errezc, M.A., Breyssed, D., Grig-
oriue, M., Zabaras, N.: Probability and Materials: from Nano- to Macro-Scale: A sum-
mary. Prob. Engrg. Mech. 21(3), 193–199 (2006)
27. Gross, B.: Least squares best fit method for the three parameter Weibull distribution:
analysis of tensile and bend specimens with volume or surface flaw failure. NASA TM-
4721, 1–21 (1996)
28. Harlow, D.G., Smith, R.L., Taylor, H.M.: Lower tail analysis of the distribution of the
strength of load-sharing systems. J. Appl. Prob. 20, 358–367 (1983)
29. Kawakubo, T.: Fatigue crack growth mechanics in ceramics. In: Kishimoto, H., Hoshide,
T., Okabe, N. (eds.) Cyclic Fatigue in Ceramics, pp. 123–137. Elsevier Science B. V. and
The Society of Materials Science, Japan (1995)
30. Kaxiras, E.: Atomic and Electronic Structure of Solids. Cambridge University Press,
Cambridge (2003)
31. Krausz, A.S., Krausz, K.: Fracture Kinetics of Crack Growth. Kluwer Academic Pub-
lisher, Netherlands (1988)
32. Le, J.-L., Baˇzant, Z.P.: Finite weakest link model with zero threshold for strength distri-
bution of dental restorative ceramics. Dent. Mater. 25(5), 641–648 (2009)
33. Le, J.-L., Baˇzant, Z.P., Bazant, M.Z.: Crack growth law and its consequences on lifetime
distributions of quasibrittle structures. Journal of Physics D: Applied Physics 42, 214008,
8 (2009)
34. Lohbauer, U., Petchelt, A., Greil, P.: Lifetime prediction of CAD/CAM dental ceramics.
Journal of Biomedical Materials Research 63(6), 780–785 (2002)
35. Mahesh, S., Phoenix, S.L.: Lifetime distributions for unidirectional fibrous composites
under creep-rupture loading. Int. J. Fract. 127, 303–360 (2004)
36. Melchers, R.E.: Structural Reliability, Analysis & Prediction. Wiley, New York (1987)
37. Munz, D., Fett, T.: Ceramics: Mechanical Properties, Failure Behavior, Materials Selec-
tion. Springer, Berlin (1999)
