Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Reliable Optimal Design in Contact Mechanics 29

2 Formulation of the Problem

Consider in rectangular coordinate system 0xyz the equilibrium of a rigid punch

interacted without friction with an elastic half-space. The plane

0xy bounding

elastic half-space

0z ≥ and denoting by Ω contains the domain of contact

f

Ω

(base of the punch), the regions of external forces

()

,

i

qxy application

i

q

Ω

(

1,2,...,im= ) and the domain

0

Ω that is free of loads, i.e.

0fq

Ω=Ω +Ω +Ω , where

i

qq

Ω= Ω∪ . Here we suppose that 0

i

fq

ΩΩ=∩

for

1,2,...,im= . The punch is in equilibrium under applied external forces and

moments and reaction of the elastic medium. Surface of the punch is described by

the equation

()

,zfxy= ,

()

,

f

xy∈Ω . Boundary conditions for considered

problem of the theory of elasticity are written in the case of frictionless contact in-

teraction as

() ()

, , 0, 0, ,

xz yz f

w f xy xy

σσ

= = = ∈Ω

(1)

()

0

0, 0, 0, ,

zz xz yz

xy

σσσ

= = = ∈Ω

(2)

() ()

, , 0, 0, ,

i

zz i xz yz q

qxy xy

σσσ

= = = ∈Ω

(3)

where

1,2,...,im= and m - given number. The normal component w of the

displacement vector is oriented in

z - direction and

kj

σ

( ,,,kj xyz= ) – com-

ponents of the stress tensor. Contact pressure is described by the function

()

,pxy,

i.e.

()

,

zz

pxy

σ

= ,

()

,

f

xy∈Ω . If the pressure distribution

()

,pxy defined

on the bottom of the punch is known, then the resulting force

P and moments

,

xy

M

M can be evaluated. In what follows we suppose that the values P ,

,

xy

M

M are given and play the role of the problem constraints. We have

() ( )

,

f

Pp pxyd P

∗

Ω

=Ω=

∫

(4)

() ( )

,

f

yfy

M

pxpxydM

∗

Ω

= Ω =

∫

(5)

() ( )

,

f

xfx

M

pypxydM

∗

Ω

=Ω=

∫

(6)

where

0, 0,, 0

yx

PM M

∗∗ ∗

≥ ≥ ≥ - given positive values.

30 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

It is required also that

() ()

,0, ,

f

p pxy xy= ≥ ∈Ω

(7)

As an optimized functional we consider the following integral

()

2

[]

f

gf

JJpf ppd

Ω

==−Ω

∫

(8)

where

()

,

g

pxy - given function characterized the required pressure distribution.

Functional (8) determines the discrepancy between the actual pressure

()

,pxy

corresponding some punch shape

()

,fxy and required pressure distribution

()

.

g

pxy. In particular, the function

g

p can be given as the constant pressure

distribution.

Let us consider the following shape optimization problem. It is required to de-

termine the function

()

,fxy describing the shape of the punch and minimizing

the discrepancy functional

()( )

min [ ] [ ]

f

JJpfJpf

∗∗

==

(9)

under conditions (1)-(7).

Formulated optimization problem (1)-(9) can be reduced to two successively

solved problems. The first problem consists in finding such contact pressure dis-

tribution

p

∗

that minimizes the discrepancy functional (8) under constraints (4)-

(7). The second problem consists in determining the shape of the punch

()

,fxy

∗

for which the obtained optimal pressure distribution

()

,pxy

∗

is realized.

3 Finding of the Optimal Pressure Distribution

To find the optimal pressure distribution

()

,pxy

∗

minimizing the functional (8),

let us consider the constraints (4)-(7) imposed on the integral characteristics (4)-

(6) and local constraint (7). To take into account the local constraint we represent

the condition (7) in the form

() ()

2

,0, ,

f

pxy xy

ψ

− = ∈Ω

(10)

where

()

,xy

ψ

- unknown variable determined in the process of solution. Con-

struct the augmented Lagrange functional

L

J for the formulated problem of pres-

sure optimization. We have

Reliable Optimal Design in Contact Mechanics 31

()

{

}

2

f

L

gf

J p p p xp yp p d

λα β χ ψ

Ω

=−−−−−−Ω

∫

(11)

where

λ

,

α

,

β

- Lagrange multipliers and

()

,xy

χ

- Lagrange function. Ex-

tremum conditions for the functional (11) with respect to variables

p and

ψ

are

written in the form

()()

1

,,

2

gf

pp x y xy

λα β χ

= + + + + ∈Ω

(12)

()

0, ,

f

xy

ψχ

= ∈Ω

(13)

The pressure distribution (12) contains the unknown values

λ

,

α

,

β

,

χ

. To

determine the constraints

λ

,

α

,

β

we can use the equalities (4)-(6). The func-

tion

χ

is found with the help of (13). Using the condition (13) and representation

() ()

2

,,pxy xy

ψ

= we can find that

()

,0xy

χ

= for

()

,

ff

xy

+

∈Ω ⊂Ω ,

if

()

,0xy

ψ

≠ . If

()

,0xy

ψ

= , then

()

,0pxy= for

()

,

ff

xy

−

∈Ω ⊂Ω .

In general case we can divide the original domain

f

Ω into two sub-domains

f

+

Ω ,

f

−

Ω (

ff f

+−

Ω+Ω=Ω), where

()

,0pxy> (

()

,

f

xy

+

∈Ω ) and

()

,0pxy= (

()

,

f

xy

−

∈Ω ).

Taking into account (10), (12), (13) we will have the following expression for

the optimal pressure distribution in the domain

f

Ω

() ()

{

}

,max0, ,pxy p xy

+

∗

=

(14)

() ()()

1

,,

2

g

pxy pxy x y

λα

β

+

=+++

(15)

The operation

max in (14) means that we choose the maximum of two values

written in parentheses. The unknown Lagrange multipliers are found with the help

of the linear system of algebraic equations

()

22

g

yx

g

yyxy y yy

g

xxyx x xx

SSSPPP

SIIM MM

SI IM MM

λαβ

+++ ∗+

++ + ∗+

++== −

++ = = −

++= = −



(16)

32 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

where the contact area

S

+

, the statical moments

y

S

+

,

x

S

+

, the moments of inertia

x

I

+

,

y

I

+

,

xy

I

+

and the values P

+

,

y

M

+

,

x

M

+

are determined as

22

,,

ff f

yx

yx xy

gg g

gygxg

S dxdy S xdxdy S ydxdy

I x dxdy I y dxdy I xydxdy

P p dxdy M xp dxdy M yp dxdy

++ +

ΩΩ Ω

+++

ΩΩ Ω

++ +

ΩΩ Ω

= = =

∫∫ ∫

∫∫∫

∫∫ ∫

(17)

Let the contact pressure is positive (

0p > ) in the domain

()

ff f

+

Ω Ω =Ω and

this domain is symmetrical with respect to the axes

x and y . Then

0

xyxy

ssI== = and we have

2

2, ,

y

x

yx

M

P

II

λα β

= = =



(18)

If in addition the function

()

,

g

pxy is also symmetrical with respect to x and

y then the following equalities will be satisfied

0, 0

2

,

ff

gg

yg x g

y

x

yx

M xp dxdy M yp dxdy

M

II

αβ

ΩΩ

∗

== ==

= =

∫∫

(19)

Consider the case when the middle pressure

()

1

,

f

m

p p x y dxdy

S

Ω

=

∫

is taken as a required pressure distribution

()

,

g

pxy, i.e.

()

,,,0

f

gm g

P

p p P p x y dxdy P P

S

∗

∗∗

Ω

= = = = =

∫



(20)

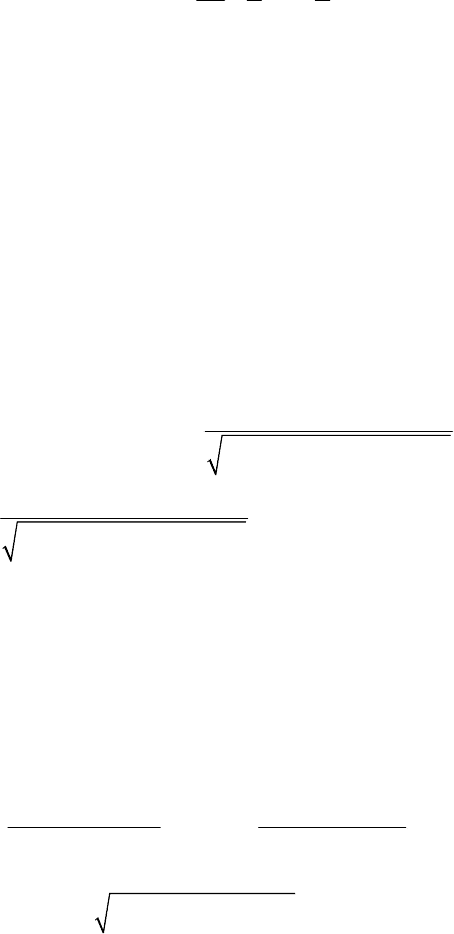
Reliable Optimal Design in Contact Mechanics 33

In this case we obtain

()

11

0, ,

22

P

pxy x y

S

λα

β

∗

= = + +

(21)

4 Determination of the Optimal Punch Shape

The direct determination of the optimal punch shape is reduced to the following

boundary value problem. It is required to find normal displacements

()

,,0wxy

defined in the contact domain

f

Ω and corresponding boundary conditions (2), (3)

and

() ()

,, 0, 0 ,

zz xz yz f

pxy xy

σσσ

∗

= = = ∈Ω

(22)

The solution of the boundary value problem of the theory of elasticity is found

with the help of potential of “simple layer”

()

,,xyz

ω

and is written as

()()

()

()()

()

()()

22

2

22

2

1

,

,, ,,

,

f

i

q

m

i

pxydxdy

wxyz xyz

xx yy z

qxydxdy

xx yy z

κω κ

κ

∗

Ω

=

Ω

′′ ′′

== +

′′

−+−+

′′ ′′

+

′′

−+−+

∫

∑

∫

(23)

where

()

2

1/E

κνπ

=− . Consequently, the optimal punch shape corresponding

to the optimal contact pressure

()

,pxy

∗

′′

and given normal loads

()

,

z

qxy

′′

applied to the region

q

Ω can be represented in the form

()() () ()

()

1

, , ,0 , ,0 , ,0

,,

,

,, , ,, ,

i

f

q

m

pq

i

pq

fxy xy xy xy

p x y dx dy q x y dx dy

xyxy xyxy

κω κ ω ω

ωω

ρρ

∗

=

∗

Ω

⎡

⎤

== +

⎢

⎥

⎣

⎦

′′ ′′ ′′ ′′

= =

′′ ′′

∑

∫∫

(24)

Here

()()()

22

,, ,xyx y x x y y

ρ

′′ ′ ′

=−+−

. The influence of the external

loads

()

,

i

qxy on the optimal shape is described by the terms

34 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

() ( )

, , ,0 , 1,...,

ii

qq

fxy xy i m

κω

= =

(25)

and the term

() ( )

,,,0

pp

fxy xy

κω

∗∗

=

(26)

determines the optimal shape in the case

0, 1,...,

i

qim= = , i.e.

() () () () ()

1

,,,, ,

i

m

pqp q

i

f xy f xy f xy f xy f xy

∗∗

∗

=

=+=+

∑

(27)

If the external loads are represented by the pointed forces

() ( )( )

,,,,

i

iiiiiiq

qxy Q xxy y xy

δ

=−− ∈Ω

(28)

then, as it follows from (25), (28) and (24), we have

()

()()()

1

22

,

,, ,

m

i

q

i

ii

ii i i

Q

fxy

xyx y

xyx y x x y y

κ

ρ

=

=−+−

∑

(29)

Consider the case of rectangular (in plane) punch

()

,

f

axabybΩ −≤≤ −≤≤

where

,ab - given values. Suppose that

()

, const 0

g

pxy=>

(30)

and introduce the notation

111

,,

222

g

Cp A B

λα

β

= + = =

In this case the optimal pressure distribution is given by a linear function of the

independent coordinates

,xy

′′

, i.e.

()

,p x y C Ax By

∗

′′

=+ +

(31)

Reliable Optimal Design in Contact Mechanics 35

Corresponding solution for

()

,

p

fxy

∗

has been found by Banichuk (2009) and

has the explicit form

()()() ()

() () () ()

0

011 22 33 44

22 22

11 22 33 44

11

,,,

22

1

,,,,

2

,,,,

pCs

C

s

f C Ax By D x y AD x y BD x y

D t xy t xy t xy t xy

Dtgxytgxytgxytgxy

κ

ϕϕϕϕ

∗

⎧⎫

=++ + +

⎨⎬

⎩⎭

=+++⎡⎤

⎣⎦

=+++

(32)

−1

−0.5

0

0.5

1

−1

0

1

3.5

4

4.5

5

5.5

6

6.5

7

x

y

f

Fig. 1. Optimal shape f without outside contact domain loading

()

0

γ

= .

36 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

Here we use the following notations

1234

22 22 22 22

134223314412

1341224 2

31231134

34

42 41

12

3442 41

,,,,

2, 2,

ln , ln

t axt byt axt by

tt tt tt tt

gtg t

gtgt

t

tt

tt t

ρρρρ

ρρ ρρ

ρ

ρρ

ϕϕ

ρρ ρ

= − = − = + = +

= + = + = + = +

=+− =+−

⎛⎞

+

++

= =

⎜⎟

−− −

⎝⎠

23

4331

2214

34

2214 4331

,

ln , ln

t

tt

tt tt

ρ

ρρ

ϕϕ

ρρ ρρ

⎛⎞

+

⎜⎟

−

⎝⎠

⎛⎞

++

= =

⎜⎟

−− −−

⎝⎠

(33)

−1

−0.8

−0.6

−0.4

−0.2

0

0.2

0.4

0.6

0.8

1

−1

0

1

3.5

4

4.5

5

5.5

6

6.5

7

7.5

y

x

f

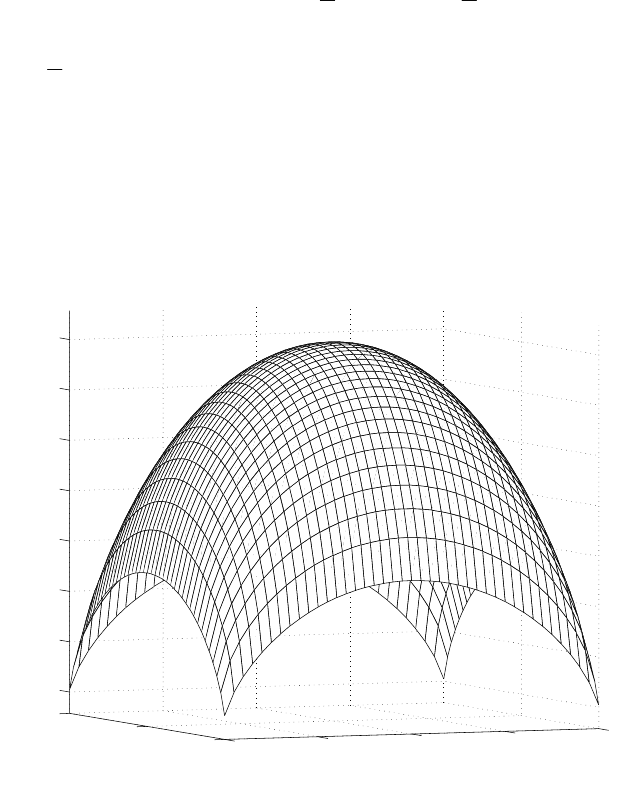
Fig. 2. Optimal shape f for the only force applied outside contact domain at the point

()

2, 0xay==, when 1

γ

= .

Reliable Optimal Design in Contact Mechanics 37

Let us present some particular examples for rectangular punch

(

,axabyb−≤≤ −≤≤), when

0, 0, ,

xy g

P

MMPPp

S

∗

∗∗ ∗

= = = =

(34)

and consequently, as it is seen from (16)-(21), we have (

0

xy

PM M===

 

)

()

0, ,

P

pxy

S

λαβ

∗

=== =

(35)

Consider at first the case of action of one pointed load

()

1

,qQxcy

δ

=− applied at

the point

()

11

,0xcy ca= = > . With the help of (27), (29), (32), (33) we obtain

()

0

2

,

pq g

g

Q

ff f pDxy

pxc y

κ

∗

⎡⎤

⎢⎥

=+= +

⎢⎥

−+

⎣⎦

(36)

−1

−0.5

0

0.5

1

−1

0

1

5

6

7

8

9

10

y

x

f

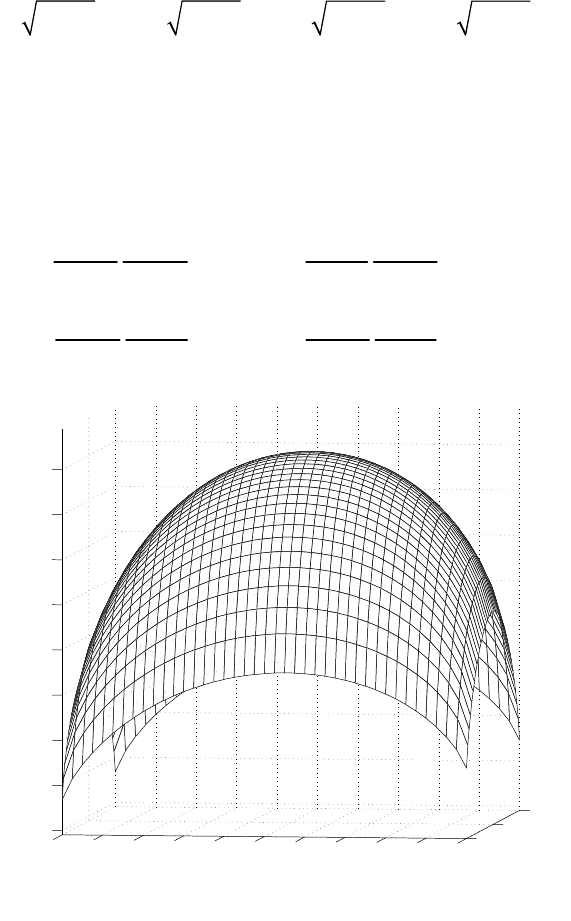
Fig. 3. Optimal shape f for the only force applied at the point

()

2, 0xay==, when

5

γ

= .

38 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

Using the dimensionless values

2

,, ,

gg

xy f Q

xy f

aaap ap

γ

κ

= = = =





(37)

we present at fig. 1, fig. 2 and fig. 3 the optimal shape

()

0

2

,fDxy

c

xy

a

γ

=+

⎛⎞

−+

⎜⎟

⎝⎠





(38)

Presented optimal shapes correspond to the following parameters:

0, .0, 5.0

γ

= 1 ;

/

1ba= ;

/

2ca= ; 11x−≤ ≤



; 11y−≤ ≤



. (The tilde

at all figures is omitted). Note that the optimal shape shown in fig. 1 when

0

γ

=

(the punch is free of outside contact domain loadings) is symmetrical with respect

to the coordinates

x and y .

−1

−0.5

0

0.5

1

−1

−0.5

0

0.5

1

13.5

14

14.5

15

15.5

16

16.5

17

x

y

f

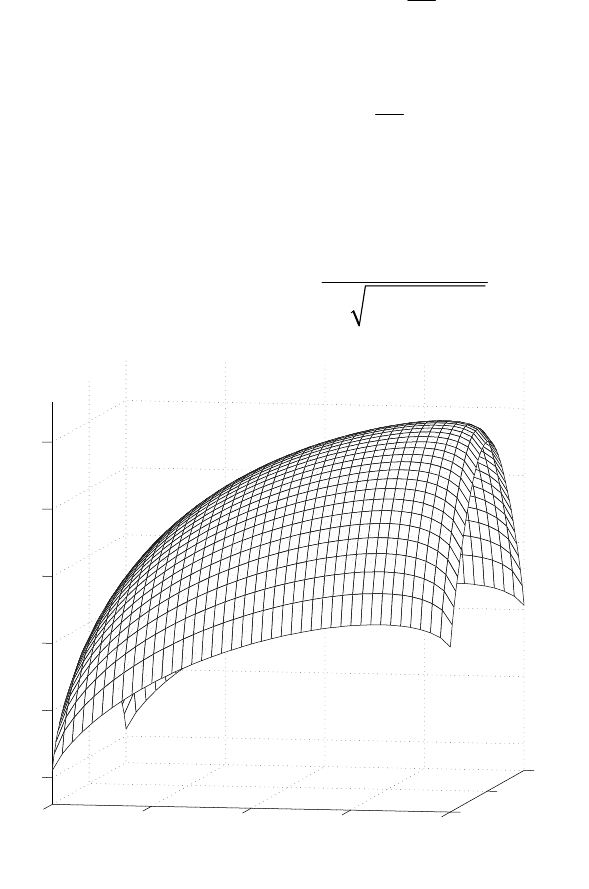
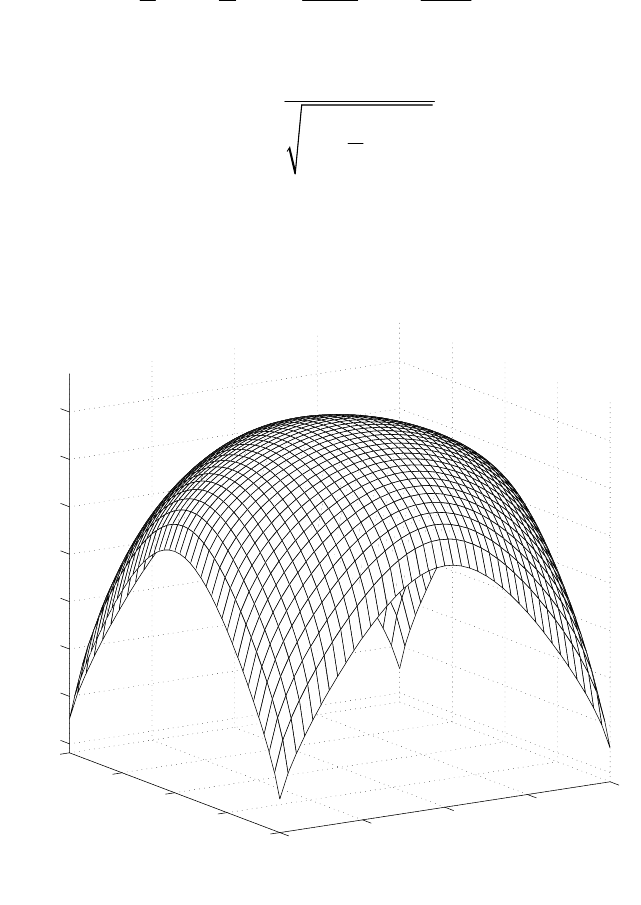
Fig. 4. Optimal shape f under loading of four pointed forces

()

2, 0xay==,

()

2, 0xay=− = ,

()

0, 2xyb==,

()

0, 2xyb==−applied outside contact

domain, when

5

γ

= .

Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.