Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

An Asymptotic Method of Boundary-Value Problems Solution of Elasticity Theory 19

of plates. The next approximations make the results according to classical theory

more precise.

The boundary layer for plates and shells consists of plane and antiplane

(boundary torsion) boundary layers. The structure of the generalized plane bound-

ary layer is analogous to the structure in the plane problem, and the values of the

antiplane boundary layer diminish when removing from the lateral surface

0=x

⎟

⎠

⎞

⎜

⎝

⎛

−

exp

and

⎟

⎠

⎞

⎜

⎝

⎛

−

exp

(36)

corresponding to the symmetric (tension-compression) and antisymmetic (bend)

space problems.

Kirchhoff-Love classical theory of plates does not take into account these

boundary layers. E. Reissner and S.A. Ambartsumyan precise theories take into

account the antiplane boundary layer and its influence on the inner stress-strain

state.

4 The Solution of the Second and Mixed Space

Boundary-Value Problem for Thin Bodies

Classical and precise theories of beams, plates and shells consider only one class

of problems – when on the facial surfaces of a thin body the values of the corre-

sponding stresses tensor components are given. Under other conditions on the fa-

cial surfaces, for example, when the values of displacements are given, or on one

surface the values of stresses and on the opposite surface displacements are given

the corresponding solutions have not been obtained yet.

It is proved that for this class of problems hypotheses of classical and precise

theories are not applicable [1]. For solving these classes of problems the asymp-

totic method has appeared to be very effective. Principally new asymptotics for

stresses and displacements, permitting to obtain solutions of not only plane but

also space problems for thin bodies, including anisotropic (21 constant of elastic-

ity) and layered problems [1,5].

Let us illustrate possibilities of the method by the solutions of the second and

mixed space boundary-value problems of thermoelasticity theory for anisotropic

plates.

It is required to find in the area

,,0,0:),,{( hzhbyaxzyxD ≤≤−≤≤≤≤= )},min(, bah =<< AA

busy with the plate of the thermoelasticity equations solution by Duhamel-Neuman

model of an anisotropic body:

equations of equilibrium

),,(,0),,( zyxzyxF

zyx

∂

(37)

20 L.A. Aghalovyan

correlations of thermoelasticity

θασσσσσσ

23464544342414

332211321

11161514131211

),,;,,;,v,;,,(

++++++=

∂

++++++=

∂

xyxzyzzzyyxx

iii

xyxzyzzzyyxx

aaaaaa

aaaaaawuzyx

aaaaaa

),,;6,5,4;,,;,,(

121323

ααα

wvuzyx

(38)

Satisfying the boundary conditions

),(),,(),,(v),,(v),,(),,( yxwhyxwyxhyxyxuhyxu

−−−

=−=−=−

(39)

),(),,(),,(),,(),,(),,( yxhyxyxhyxyxhyx

zzzzyzyzxzxz

+++

===

σσσσσσ

(40)

),(),,(),,(v),,(v),,(),,( yxwhyxwyxhyxyxuhyxu

+++

===

(41)

and the conditions on the lateral surface, which for now are considered to be

arbitrary.

In the equations (37), (38) passing to dimensionless coordinates and displace-

ments

AAAAA /,/v,/,/,/,/ wWVuUhzyx ======

, we

again obtain singularly perturbed by small parametre

A/h=

system, the solu-

tion of which has the form of (1), but, for

int

I asymptotics (4), (33) is not admis-

sible, which indicates inapplicability of the hypotheses of classical theory for the

solution of the above formulated problems. For their solution asymptotics is

applicable

0,1

,v,

=−=

(42)

Substituting the representation (4), (42) into transformed system (37), (38) we get

a recurrent system for determining

),,(

)(

ζηξ

Q . The solution of this system

will contain six arbitrary functions, which are uniquely determined from condi-

tions (39), (40) or (39), (41).

This class of problems differs from classical by this, too, as the solution

int

becomes fully known. Rising residual on the lateral surface is removed by the so-

lution for the boundary layer, which does not influence on the solution of the inner

problem any more. If the functions ),( yxQ

entering conditions (39)-(41) are

polynomials, the iteration process cuts off and we obtain a mathematically precise

solution of the inner problem (solution for layer).

We derive it for the plate with general anisotropy, corresponding the problem

(39), (40), when

constwu

zzyzxz

====

+++−−−

σσσ

,,,0v :

An Asymptotic Method of Boundary-Value Problems Solution of Elasticity Theory 21

))((

))((v

))((

353433

454443

555453

656463

252423

151413

+++

+++=

===

++=

xzyzzz

zzzzyzyzxzxz

xzyzzzxy

xzyzzzyy

xzyzzzxx

AAAhzw

AAAhz

AAAhzu

AAA

σσσ

σσσσσσ

σσσσ

(43)

where

1266

1622

2611261612662211

662211

6,2,1,,,/)(

)(,/)(

5,4,3,,

aaaaaaaaaaaa

kjiaaaB

ikjiaaaaB

aAAAaAaA

mlBABaBaA

ijjjiikk

kkijjkikij

mllmlmlmml

klklklkl

−−−+=Δ

=Δ−=

≠≠≠Δ−=

+++=

=−−−=

(44)

For orthotropic plates we have

)(),(v),(

0,,

2313

zhAwzh

zzzzyzyzxzxz

xyzzyyzzxx

+=+=+=

===

+++

σσσσσσ

σσσσσ

(45)

1222111332323131333

1231113122311322231213

/)(,/)(

aaaaAaAaA

aaaaAaaaaA

−=Δ++=

Δ−=Δ−=

Boundary conditions (39), (41) at

0v ≡==

−−−

wu , constwu =

+++

,v, for

orthotropic plates the precise solution corresponds

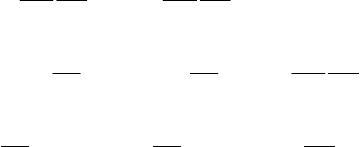
22 L.A. Aghalovyan

)(

),(

v),(

2313

wzh

zzyzxz

xyyyxx

+=+=+=

===

+++

σσσ

(46)

Asymptotics (4), (42) is applicable for the solution of the second and mixed

boundary-value problems of layered anisotropic plates, as well as for shells [5].

5 Solutions of Plane and Space Dynamic Problems

The asymptotic method is especially effective for the solution of the problems on

forced vibrations of thin bodies.

Consider forced vibrations of orthotropic beams-strips

hyxyxD ≤≤≤= ||,0:),{( A

}A<<h

with the series of the boundary conditions on the facial surfaces

hy ±=

tixXhx

Ω±=±

exp)(),(

tixYhx

Ω±=±

exp)(),(

(47)

tixYxXhxhx

yyxy

Ω=

exp))(),((),(),,(

σσ

0),(v,0),( =−=− hxhxu

(48)

tixxuhxhxu Ω=

exp))(v),((),(v),,(

0),(v,0),( =−=− hxhxu

(49)

where

++±±

v,,, uYX are known functions, Ω is the frequency of the forcing

action. It is considered that the beam is in the conditions of the plane deformation.

The solution of dynamic equations of the plane problem of elasticity theory will

be sought in the form of [6,7]

))exp(),(),,((),,(v),,,(

2,1,;,,),exp(),(),,(

tiyxuyxutyxtyxu

kjyxtiyxtyx

Ω=

==Ω=

αβ

(50)

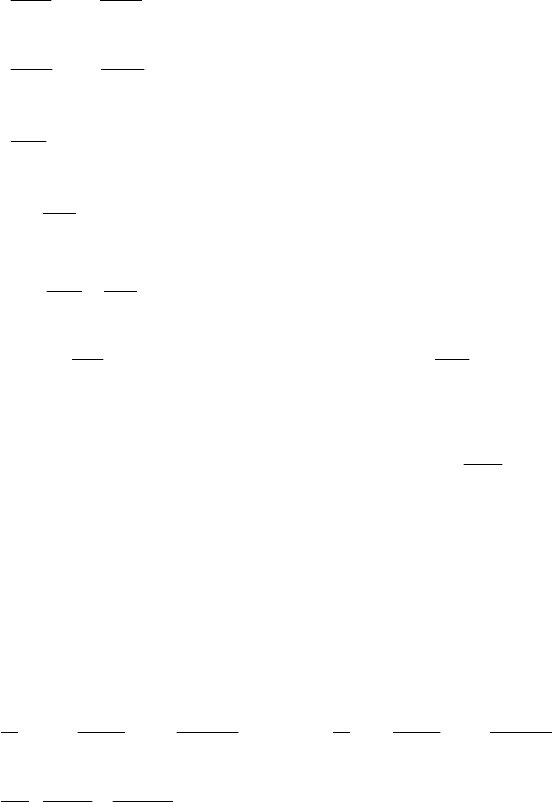
An Asymptotic Method of Boundary-Value Problems Solution of Elasticity Theory 23

Substituting (50) into the equations of dynamic problem, then passing to dimensionless

variables

hyx /,/ ==

A and displacements AA /,/

uVuU == , we

obtain a singularly perturbed by small parametre

A/h=

system

=Ω+

∂

=Ω+

∂

−−

22121111

σβσβ

∂

22221112

σβσβ

∂

−

663333

222

*1266

,2,1,,),(

akjaaaa

kjjkjk

==−=

Ω=Ω=

∂

−

ρσ

ξζ

(51)

The solution of system (51) has the form (1), where

NsVUVU

ssss

,0),,(),(),,(

)()()(1int

===

+−

εζξσεσ

(52)

Note a very important fact – asymptotics (52) of the dynamic problem solution

principally differs from asymptotics (4), (5) of the corresponding static problem.

Asymptotics (52) is universal, as it remains unchangeable in all dynamic plane

and space boundary-value problems for thin bodies – beams, plates and shells.

Substituting (52) into (51) from the obtained system it is possible to express

)(s

)()(

VU :

00,,

)(2

122211

)1()(

)(

)1(

)(

)1(

)(

<≡−=Δ

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

−−

matQ

UVUV

βββ

ξζ

βσ

(53)

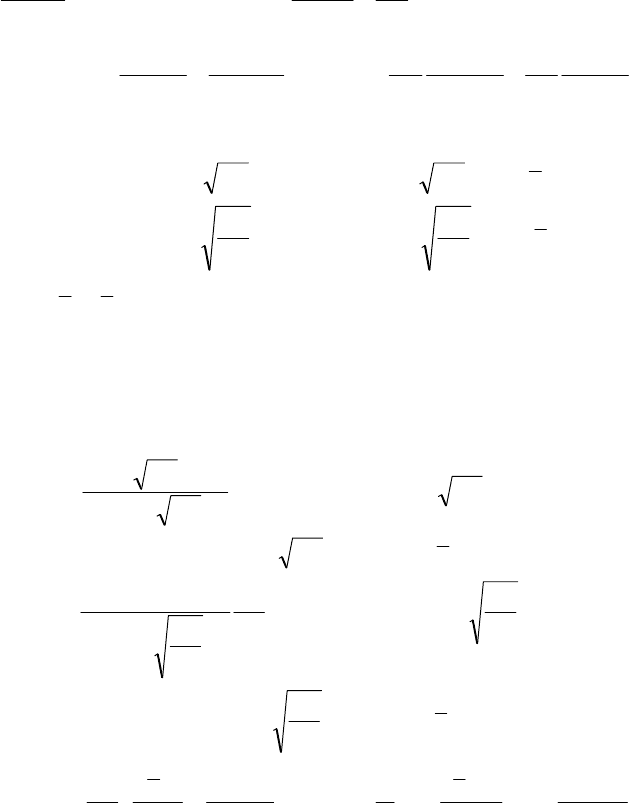
24 L.A. Aghalovyan

Values

)()(

VU are determined from the equations

βζξβ

ζξξ

βζζ

∂

∂Δ

−

∂∂

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂∂

∂

−=

=Ω

∂

=Ω+

∂

−−−− )1(

)1(2

)(

)1(2)1(

)(

)(2

)()(2

*66

)(2

fUa

(54)

The solutions of equations (54) are

)(

*66

)(

2*66

)(

vcos)(sin)(

cos)(sin)(

ssss

CCV

uaCaCU

+Ω

+Ω+Ω=

ζζ

ζζζξ

(55)

where

)()(

u are the particular solutions of equations (54).

Four functions

)(

C are determined from the conditions for each group of

equations (47)-(49). For example, applying (53), (55) satisfying conditions (47),

we find

)(

C , substituting them into (55), we determine the following solu-

tion of the inner problem

),(v)]1(cos))1,((

)1(cos))1,([(

2sin

),()]1(cos))1,((

)1(cos))1,([(

2sin

)(

)()(

)(

*66

)()(

*66

)()(

*66*

66)(

ζξζ

ζξζξ

ζξ

sss

fYV

uafX

afX

+−Ω

−++

++Ω

−

−=

+−Ω−++

++Ω−

ΩΩ

−=

−

(56)

0,0,,

)()()0()0(

)1(

)(

)1()(

)(

2212

≠====

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

±±±±±±

−−−

sYXYYXX

εε

ξζ

σσ

In the analogous way the solutions corresponding conditions (48), (49) are written

out. From the solution (56) it follows, that the solution of the dynamic inner problem

is fully determined from the conditions on the longitudinal boundaries

hy ±= ,

unlike the first static boundary-value problem (2). Therefore, the dynamic boundary

An Asymptotic Method of Boundary-Value Problems Solution of Elasticity Theory 25

layer will not influence on the solution of the inner problem and will remove the

residual on the transversal edges

A,0=x i.e. on the lateral surface. Solution (56)

will be final, if

0/2sin,02sin

*11*66

≠ΩΔ≠Ω

These conditions are broken, when the value

Ω coincides with the frequency

value of the free vibrations, then a resonance will arise.

Again, if the functions

±±

YX , are polynomials, iteration process cuts off and

mathematically exact solution of dynamic problem for layer is obtained.

In space dynamic problems for plates and shells, including layered, asymptotics

(50), (52) is preserved for all stresses

)3,2,1,(, =kj

and displacements

wu ,v, . By the above described procedure the solutions of the three-dimensional

problem equations satisfying space boundary conditions on the facial surfaces,

like conditions (47)-(49) are determined. We bring this solution for an orthotropic

plate

,0:,,{ axzyxD ≤≤=

}),,min(;,0 AA <<=≤≤−≤≤ hbahzhby

corresponding to the conditions

constwutiwuwuhz

zzyzxz

=Ω=−=

====

−−−−−−

,v,),exp(),v,(),v,(:

(57)

particularly, simulating behaviour of the constructions foundations and airfields

flying strips on the seismic actions

),;v,(),1(cos

2cos

3,2,1,),exp(

),v,,(),exp(

445555*

55*

aaua

kjtiwutiuu

jkjk

−Ω

=Ω=Ω=

−

)1(cos

cos

∂

−=

∂

−=

∂

−=

−

(58)

1233

1322

2311132312332211

23121322231312231113

12221111

/)(,/)(,/)(

aaaaaaaaaaaa

aaaaAaaaaAaaaA

−−−+=Δ

Δ−=Δ−=Δ−=

By the asymptotic method the solutions of the space dynamic problems for layered

plates [8] and shells [9] can be written out, as well.

26 L.A. Aghalovyan

6 Conclusions

An asymptotic method for the solution of two-dimensional and three-dimensional

static and dynamic problems of elasticity theory for isotropic and anisotropic thin

bodies is expounded. The effectiveness of the method for the solution of new

classes of thin-body problems – in particular, for those problems that cannot be

solved by the classic and refined theories, is illustrated.

References

1. Aghalovyan, L.A.: Asymptotic theory of anisotropic plates and shells, p. 414. Nauka,

Fizmathlit, Moscow (1997)

Vazov, V.: Asymptotic decompositions of solutions of ordinary differential equations,

p. 464. Mir, Moscow (1968)

Nayfeh, A.H.: Perturbation methods, p. 455. John Wiley and Sons, Chichester (1973)

Vasiljeva, A.W., Boutuzov, V.F.: Asypmtotic decompositions of solutions of singularly

perturbed equations, p. 272. Nauka, Moscow (1973)

Aghalovyan, L.A., Gevorgyan, R.S.: Nonclassical boundary-value problems of anisot-

ropic layered beams, plates and shell, p. 468. Yerevan, Publish. House, Gitutjun, NAS

of Armenia (2005)

Aghalovyan, L.A.: An asymptotic method for solving three-dimensional boundary value

problems of statics and dynamics of thin bodies. In: Proceed. of the IUTAM symposium

on the relations of shell, plate, beam, and 3D models, pp. 1–20. Springer, Heidelberg

(2008)

Aghalovyan, L.A.: On one method of solution of three-dimensional dynamic problems

for layered elastic plates and applications in seismology and seismosteady construction.

In: Proceeding European Conference on Structural Control, vol. 1, pp. 25–33. Saint-

Petersburg, Russia (2008)

Aghalovyan, L.A., Hovhannisyan, R.Z.: Theoretical proof of seismoisolators applica-

tion necessity. In: Proceedings of International Workshop on Base Isolated High-Rise

Buildings, Yerevan, Armenia, June 15-17, pp. 185–199. ”Gasprint” LTD, Yerevan

(2008)

Aghalovyan, L.A., Ghulghazaryan, L.G.: Asymptotics solutions of non-classical bound-

ary-value problems of the natural vibrations of orthotropic shells. Journal of Applied

Mathematics and Mechanics 70(2006), 102–115 (2006)

Reliable Optimal Design in Contact Mechanics

Nickolay V. Banichuk, Svetlana Yu. Ivanova, and Evgeniy V. Makeev

A. Yu. Ishlinsky Institute for Problems in Mechanics,

Russian Academy of Sciences, Moscow, Russia

Abstract. The problem of contact pressure optimization is formulated for the case

of rigid punch interacted with elastic medium. Coupling of the punch penetration

and action of external loads at the outside regions is taken into account. The shape

of the punch is considered as an unknown design variable. The minimized integral

functional characterizes the discrepancy between the actual contact pressure and

the required pressure distribution. The problem is studied under condition that the

total forces and moments applied to the punch and the loads acted at the outside

regions are given. It is shown that the considered optimization problem can be

splitted and transformed to two successively solved problems. Optimal shapes are

found analytically for the punches having rectangular contact domains.

1 Introduction

In the engineering and mathematical literature there are many results concerning

the shape optimization in contact problems of the theory of elasticity (see, for ex-

ample, Contry and Sereig (1971), Haug and Kwak (1978), Paczelt (1980), Bene-

dict and Taylor (1981), Haslinger and Neittaanmaki (1984, 1986, 1987, 1988),

Haslinger et al. (1986), Paczelt and Szabo (1994)). In many papers devoted to con-

tact interaction of rigid bodies (punchs) and elastic (deformable) medium the

analysis and optimization problems were considered in the frame of static, qua-

sistatic and dynamic approaches. It was also supposed that the loading configura-

tion fully describes the distribution, magnitude and domains of application of all

the mechanical loads; no variability of the load configuration was allowed.

The problems of contact stress minimization have been rigorously formulated

and investigated by Haug and Kwak (1978). In this paper the unknown contour

was taken as a design variable and numerical optimization method was proposed.

It was shown by Benedict and Taylor (1981) that a Lagrange multiplier technique

can be used to transform the inequality equilibrium relations found for contact

problems to equality relations. Besides, an efficient numerical contact problem so-

lution based on a direct minimization of the potential energy function by a con-

strained quadratic programming algorithm was developed and demonstrated on

several examples.

28 N.V. Banichuk, S.Yu. Ivanova, and E.V. Makeev

A new optimization problem of controlling the contact pressure

p was pre-

sented by Paczelt and Szabo (1994). The minimum of the maximal contact pres-

sure

max

p was investigated under the constraints that the contact pressure should

satisfy the inequality

0p ≥ as well as the controlling condition

max

vp p≥ ,

where

()

vx is the controller function. It was also taken into account that the gap

between two bodies should be positive or zero after deformation. Some numerical

examples demonstrated of the controlling technique for the shape optimization

problem of a roller bearing were presented.

Some mathematical aspects of the shape optimization theory have been studied

by Haslinger, Neittaanmaki and Tiihonen. The existence of the optimal shapes in

contact problem was proved by Haslinger and Neittaanmaki (1984). The questions

of approximation and numerical realization were investigated by Haslinger and

Neittaanmaki (1986, 1987, 1988), Haslinger et al. (1986). Note that a nonlinear

programming approach to the contact optimization problems for elastic plates with

pointed supports has been described by Kartvelishvily (1974) and Banichuk

(1983).

After the pioneering theoretical works by Galin (1976, 1980), Galin and Gor-

yacheva (1977), the wear process was taken into account in analysis and optimiza-

tion of contact interaction. Some important results in this direction were obtained

by Goryacheva and her coworkers (Goryacheva and Chekina 1989, Goryacheva

and Dobychin 1984, Goryacheva and Torskaya 1992) and Paczelt and Mroz (2005.

2007, 2009).

Note also some new optimization problems in contact mechanics with incom-

plete data concerning external loadings studied by Banichuk and Ivanova (2009).

The purpose of this investigation is to develop an effective approach for a class

of optimal design problems for system consisting of rigid and elastic bodies inter-

acted without friction. Problems involving two loading systems are considered.

The first one consists of a given forces and moments applied to a punch and

the second one is represented by a fixed distributed loads acted at the regions out-

side the contact domain. The pressure positiveness constraint is important to the

nature of these problems imposes a unilateral constraint on the contact pressure

distribution.

A contact problem formulation that is well suited to optimal design techniques

is developed. This formulation is used to derive an effective decomposition

method and optimality conditions for contact pressure distribution. As a result of

performed decomposition of the original shape optimization problem we effec-

tively find the optimal contact pressure (at the first stage) and the corresponding

shape of the rigid punch penetrated into elastic half-space (at the second stage).

The last sub-problem is solved taking into account the application of found pres-

sure distribution in the contact domain and given normal loads in the outside re-

gions. Some analytical solutions are obtained for a rectangular (in-plane) punch

and various pointed loads.