Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Forced Vibrations of the System:

Structure – Viscoelastic Layer

Boris V. Gusev and Alexander S. Faivusovich

Moscow State University of Railway Engineering (MIIT) 125009, Moscow, Russia

Lugansk national agrarian university 91008, Lugansk, Ukraina

info-rae@mail.ru

Abstract. Analytical solutions of the problems about interrelated vibrations of an

elastic (deformable) structure with viscoelastic layer are obtained. The investiga-

tions were made to workout the method of the dynamical computations and opti-

mization of technological processes for forming of reinforced concrete articles on

the shock-and-vibration machines and shock machines. The analysis of numerical

results and experimental data are presented.

1 Introduction

The authors developed the method for dynamical computations of the system

“concrete mix – form – forming machine” (FFM) based on the solutions of 2-D

problems. This method differs from known approach, in which the vibrations of a

viscoelactic rod with point mass and elastic support is considered. It was deter-

mined by experimental and theoretical investigations that such model is suitable

for qualitative analysis of FFM dynamical behavior only. It is inadmissible to ne-

glect the bending stiffness of the tray form and its envelope in common case [1]. It

is necessary to take additionally into account the friction force on vertical walls

investigating the vibrations of high concrete articles.

2 Investigation and Analysis of the FFM Vibrations

The statement and solution of the problem for vibrations of the FFM system has

been performed taking into account a set of prepositions and assumptions concern-

ing the properties of the concrete mix and the mechanical system. These preposi-

tions are confirmed in experiments. The prepositions for the concrete mix [1, 2] are:

• the compaction process is long enough;

• the density of the mix is constant during the compaction process;

• the concrete mix is a transversely isotropic viscoelastic media;

80 B.V. Gusev and A.S. Faivusovich

• the case of the plane deformation is investigated in the absence of lateral (in

plane) mix deviations and friction in the form envelope;

• the vibrations without separations are considered.

The prepositions for the mechanical system:

• the tray of the form is rigidly connected to the forming machine;

• the structure of the tray is a periodical and consists of a homogeneous cells.

Further, the tray and envelope cells of the beam type are considered for simplifica-

tion purposes.

The vibrations of the FFM system can be considered as a superposition of vi-

brations for two particular systems:

• the tray of the form like a beam with point masses (vibroexciters, and so on) in-

teracted with a viscoelastic layer (concrete mix);

• sepateted cells of the tray envelope interacted with a viscoelastic layer.

On a first step, using the first scheme, the natural frequencies for the form with con-

crete mix and the amplitudes of forced oscillations are found. Then, using the second

scheme, the optimization of the forming regimes are performed taking into account

the possibility of the admissible closeness for the natural and forced frequencies of

the system to enhance the dynamical influence on the concrete mix [1, 2].

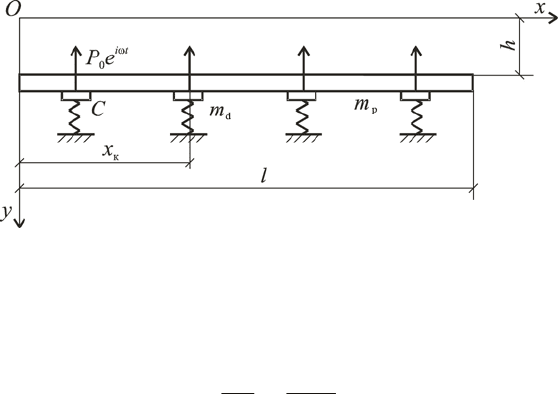
The scheme of the tray is shown in fig.1, where

m is a linear mass density of

the beam;

m is mass of devices (for example, vibroexciters); l is length of the

beam;

P is amplitude of the force of the vibroexciter; C is a rigidity of the sup-

ports (springs);

is a frequency of forced vibrations.

Fig. 1. The system “concrete mix – vibrostand”

The beam with point pass can be reduced to the equivalent one with uniform

distributed mass. In this case

()

bl bl

=+ +

∑∑

(1)

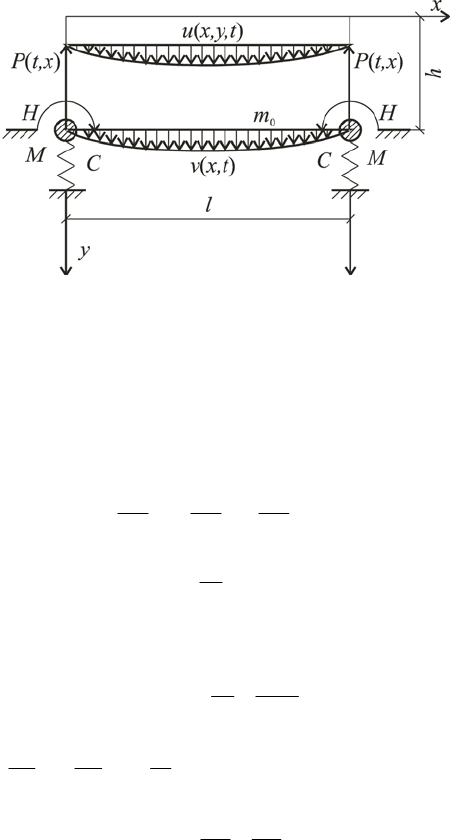
Forced Vibrations of the System: Structure – Viscoelastic Layer 81

Fig. 2. The system “concrete mix – envelope cell – forming machine”

where

x is the first derivative of the beam function in the considered point; b is

a width of the beam;

I - is a moment of inertia of the point mass

m ,

Ima=

(

a is a distance from the center of gravity of the vibroexciter to the beam axe).

The problem about steady-state vibrations of a beam interacted with viscoelas-

tic layer can be presented in the form:

222

uuu

yxt

∗

∂∂∂

(2)

0, 0,

∂

(3)

yhvu==

(4)

0, , ,

uui

xxl

xdG

∗

∂

== =

∂

(5)

() ()

vvu

yhm D bE P xxe cvxx

ytx

δδ

∗∗

∂∂ ∂

=+=+ −− −

∂∂∂

∑∑

(6)

0, , 0,

xxl

∂∂

== ==

∂∂

(7)

()

EE i

∗

(8)

()

1,GG i

∗

(9)

()

1,DD i

∗

(10)

()

cos ,

PPe t

(11)

82 B.V. Gusev and A.S. Faivusovich

where

u ,

are a strain and a density of the concrete mix, respectively;

, G are

a dynamical elasticity and shear moduli of the concrete mix, respectively;

are inelastic resistance vibration coefficients of the concrete mix; v is a beam

strain;

D is a beam stiffness;

is an inelastic resistance vibration coefficient of

the beam;

, d are a viscosity coefficient and thickness of the wall viscous layer,

respectively;

is impulse delta function; N is amount of the vibrators and point

masses.

The empirical data stated relations between structural and mechanics character-

istics of concrete mixes and initial composition which used for engineering

computations [1, 2] have been obtained based on experimental investigations of

two-phase media.

For long-term vibrations we have

()

uUxy

(12)

()

vVxe

(13)

According the method of separation of variables the solution (2) taking into ac-

count (12) and boundary conditions (3), (5) has the form:

() ()

,chcos

Uxy A y nxle

ϕπ

∞

=⋅

∑

(14)

where

() ()

Gnl E i

ωα

∗∗

⎡⎤

=± − =± +

⎣⎦

Analogously for beam:

()

vCXxe

∞

∑

(15)

The eigenfunctions

()

Xx are the fundamental beam ones for beam with free

ends:

() ( )

()

ch cos ch sin

sh sin ch cos

mmm

rx rx

Xx r r

rx rx

⎡

⎤

⎛⎞ ⎛⎞

=− +

⎢

⎥

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

⎣

⎦

⎡

⎤

⎛⎞ ⎛⎞

−− +

⎢

⎥

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

⎣

⎦

(16)

The coefficients

r are found from the following frequency equation

ch cos 1

rr=

(17)

The solution of the Eq. (6) is found as an expansion in the series over eigenfunc-

tions of the corresponded homogeneous problem.

Substituting (14) and (15) into (4) and (6) we have the system of equations

with respect to unknown

and

C , applying the numerical algorithm described in

Forced Vibrations of the System: Structure – Viscoelastic Layer 83

[1, 2] we obtain the following expression for the contact dynamical stresses

()

,,xht

as follows:

() ()

()

() ()

,, 1 cos cos ,

1,2,3, , 1,3,5, ,

mkm n

mn k

Enx

xht n x a LP T t

lm l

σπ ω

⎛⎞

=− +

⎜⎟

⎝⎠

∑∑

……

(18)

where

324 1 2n

TMM

λλλ

=+,

()

1235

11234

cos

λλλλ

ωω

⎛⎞

= − − Φ +Φ +Φ +Φ

⎜⎟

⎝⎠

()

123

21234

cos ,

λλλ

⎛⎞

=− Φ +Φ +Φ +Φ

⎜⎟

⎝⎠

10 2 3

tg , , tg ,

νω βα

Φ= Φ= Φ=

4 5 21 3425

tg tg th , tg , ,hh MM

αβ ξ

Φ = ⋅ Φ =− =Φ −Φ −Φ −Φ

()

ch cos sh sin ,

mmmmm

Lrrrr

⎡⎤

=−−+

⎣⎦

()

∑

In Eq (18)

is the eigenfrequency of the beam without loads. The amplitudes of

vibrations have finite values at resonance since

0M ≠ .

Supposing

0P = , the eigenfrequensies

f are found from the original system.

For the tray as a rectangular plate the values

f are given the formula

fGh

lbh

ππ

⎡

⎤

⎛⎞⎛⎞

=+ +

⎢

⎥

⎜⎟⎜⎟

⎝⎠⎝⎠

⎢

⎥

⎣

⎦

(19)

The frequency coefficient

is found from the characteristic equation:

пр

1, 3, 5, , 1, 3, 5, ,

ms ms

msms

Gh m s

lbm

mp ps

θθ

ππ

ρθ

⎧⎫

⎡

⎤

⎪⎪

⎛⎞⎛⎞

=+ ++

⎢

⎥

⎨⎬

⎜⎟⎜⎟

⎝⎠⎝⎠

⎢

⎥

⎪⎪

⎣

⎦

⎩⎭

== ==……

(20)

where

m is mass of the concrete mix.

84 B.V. Gusev and A.S. Faivusovich

The mathematical model of the cell of the envelope, connected to one mass vi-

brostand can be reduce to the plate model with the boundary conditions including

the equivalent mass

M and the stiffness C and H with respect to the lateral and

angular deviations (fig. 2).

For shock and vibration process analogous scheme is obtained after lineariza-

tion of the boundary conditions with respect to lateral displacements. The original

equation of motion (2) is also valid for this case. The boundary conditions have

the form [1, 2]:

()

24 2 2

24 2

,,,

vv u u

yhm D bE Pxt

yttx y

⎡⎤

∂∂ ∂ ∂

=+=++

⎢⎥

∂∂∂∂ ∂

⎣⎦

322

101

322

0, 0, 0,

vvvv

xDCvM DH

xxtx

∂∂∂∂

=−−=−=

∂∂∂∂

322

101

322

,0,0.

vvvv

xl D CvM D H

xxtx

∂∂∂∂

=++= +=

∂∂∂∂

Here

D is a bending stiffness of the cell.

For the cases of vibration, shock and vibration, and shock effects the value

()

,Ptx is equal, respectively

() () ( )

,Re ,

Ptx Pe x l x

δδ

=+−

⎡

⎤

⎣

⎦

(21)

() ()

()

,cos,

jm m j

Ptx B X x tT

∞

∑

(22)

() ( )

Ptx R t rT

∞

=−

∑

(23)

where

()

is the impulse delta function,

is impulse of force.

Eq (22) is obtained by expanding the periodical function in Fourier expansion.

For the case of shock effects the initial conditions have the form:

0, 0 ,tyh=≤≤

(24)

,0 .uy v y h∂∂= ≤≤

(25)

When H

=∞ the eigenfunctions for the cell are

() ( ) () ()

Xx Skx Vkx Ukx

=− +

(26)

where

()

Skx,

()

Ukx,

()

Tkx,

()

Vkx are the Krylov beam functions.

Forced Vibrations of the System: Structure – Viscoelastic Layer 85

()

() ()

632

53 2

пр 1

kT k kCS k CV k

kV k kCT k kCU k

Mml C C l D

=− −

−

(27)

where

m is the linear mass density of the envelope.

The eigenvalues

k are found from the following equation

()( )

2sh sin

ch cos 1 cos sh ch sin 0, .

Qk k kk k k QCk

⋅

+⋅−+⋅+⋅==

(28)

For the case of shock and vibration effects the contact dynamical pressures are

equal to:

()

1,3,5 1

cos th

mj m n n

mn j

EB n R h e

xht

lm bE

πϕϕ

ωω

∞

−

== =

∗

⋅

⎡

⎤

−−−

⎢

⎥

⎣

⎦

∑∑

(29)

where,

() () ()

mm m m

mmm

RTk Sk Vk

kkk

⎧⎫

=−−+

⎡⎤

⎨⎬

⎣⎦

⎩⎭

= ,

B are the

coefficients of the expansion of the periodical function (22).

Compaction of concrete mixes under shock actions can be considered as a de-

forming process of a concrete layer loading by a set of shock impulses sequen-

tially imposed with time interval T .The stresses arisen after such action can be ar-

ithmetically summed since the maximum of dynamical pressures achieves in a

time interval just after the impulse action.

The solution of the corresponded problem written in displacement form for the

case of hinge-supported cell under instantaneous impulse can be presented as

()

1,3,5 1

22 22

,, cos cos sin ,

16 sin

sin

mn n

nm r

mn mn

mn n

uxyt A ye t rT

EmG m

λμ λ

αμ

πϕ λ

μλ

λπ π

ρρ ρρ

−

∞

−

== =

=−

=+ =

⎛⎞

⎜⎟

⎝⎠

⎛⎞

=+−+

⎜⎟

⎝⎠

∑∑

(30)

86 B.V. Gusev and A.S. Faivusovich

The corresponded frequency equation at

μμ

== is reduced to the form

бб

,, ,

Gh m

mEl

PhP

θθ

θλ

⎛⎞

=+ +

⎜⎟

⎝⎠

===⋅

(31)

where

m is the linear mass density of the viscoelastic layer.

The analysis of the solutions (18), (29), (30) shows that the distribution of dy-

namical pressures along the height of a layer is different for these three cases. The

envelope curve of the dynamical pressures diagram has a sinusoidal character at

the vibration action, but the envelope curve is the sum of sinusoids at the shock

action (instantaneous impulse). Note, that the vibrations are in-phase along the

height of layer independently from its vertical size. But the periodical regime of

motion changes on an aperiodic one if the height of layer grows and static compo-

nent of compression arises. It leads to considerable diminish of the process effi-

ciency. So, it is necessary to diminish the vibration frequency at growth of the

height of layer.

The availability of the zones with zero points depends on the relation of the du-

ration of shock impulse on the period natural vibrations of the system.

The frequency equations characterized the eigenfrequensies for systems (20) and

(30) define the dependence between the eigenfrequencies

for free of loading and

interacted with concrete mix layer

P of the elastic system. The difference is that the

frequency coefficients for the tray are taken as ones for the beam with free ends, but

for cell of the envelope these coefficients are found from eq. (28). The character of

changing the parameter

k versus on dimensionless parameters

C and

is shown

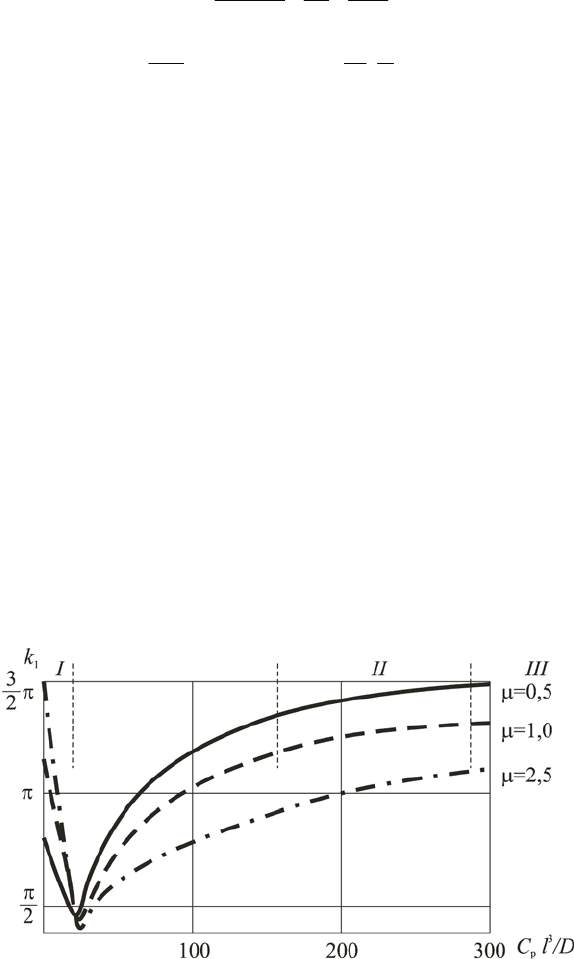
in fig. 3. The areas I, II, and III correspond approximately to the values of parame-

ters for vibration, sock and vibration, and shock machines, respectively.

Fig. 3. Dependence the frequency coefficient k

vs. on parameters μ and C

Forced Vibrations of the System: Structure – Viscoelastic Layer 87

Thereby, the obtained solutions give us possibility to show the influence

the bending stiffness, point masses, and elastic bracing on the eigenfrequencies.

The comparison the eigenfrequencies for loaded and free of loading structures al-

lows to compute the coefficient of added mass

пр

, which uses in engineering

computations:

пр

бб

⎛⎞

=−

⎜⎟

⎝⎠

(32)

The parameter

пр

depends on the mechanical properties of the mix and ratio of

linear mass densities and is unique for any concrete mix. So, implementation this

parameter as a constant (

пр

const

= ) can not ensure the satisfactory accuracy for

practical calculations.

It is followed from obtained solutions, that viscoelastic layer reduces the eigen-

values of the system. It is also determined, that the inertial resistance dominates at

0,1

hm≥ , but the influence of the mechanical properties of the mix is more es-

sential when layer thickness less than

0,1 m

The experimental investigations and numerical computations show, that the

value of dynamical stresses depends essentially on lowest eigenfrequency and in a

less degree on a correlation of frequencies in the spectrum at shock actions [1, 2].

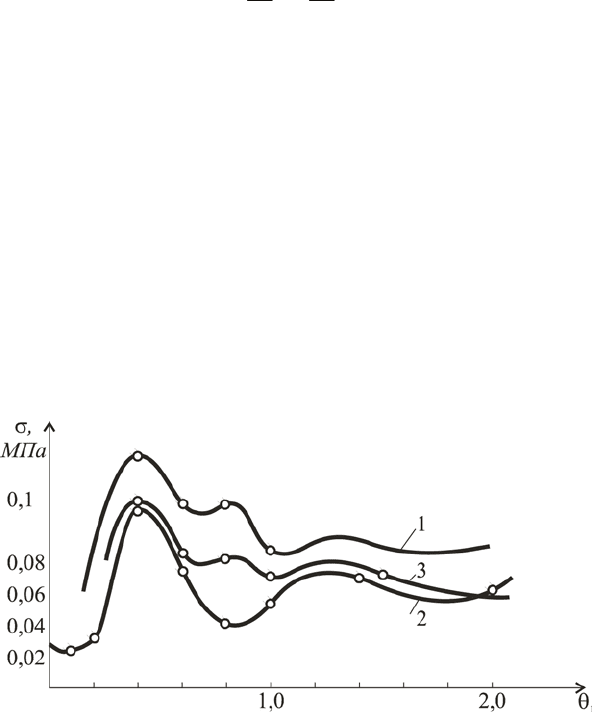
The dependence of dynamical pressure versus the dimensionless frequency

is presented in fig. 4.

Fig. 4. Dependence of the dynamical pressure vs. the frequency coefficient

. E = 7 МПа,

1– h = 0,05 м ; 2– h = 0,3 м ; 3– h = 1,0 м.

If the frequency of shock impulses is multiple to the eigenfrequency of the system

then the phenomenon of the impulse resonance can be realized. However, taking

into account the natural scatter of mechanical characteristics influencing on the

dynamical properties of the system, this phenomenon is practically unrealizable. If

88 B.V. Gusev and A.S. Faivusovich

the eigenfrequency of the layer is less than the frequency of shock impulses, then

the accumulation of the stresses of unit sign (compression) realizes, i.e., the static

component of the pressure appears when the dynamical one is not great enough. So,

the efficiency of the compaction process diminishes considerably. Limiting frequen-

cies presents in [1, 2] for which the unloading of the layer is reached in each cycle of

vibrations. Thereby, the possibility for optimization of the compaction regimes is

connected to choice of optimal values of the dimensionless eigenfrequencies

and maximal frequency of forced impacts taking into account constraints above

mentioned.

The frequency spectrum of driving force has an essential sense for shock and

vibration regimes of vibrations. The increase of dynamical impacts on the concrete

mix can be reached via approaching the eigenfrequencies to one of the driving

force harmonic. Note, that the tuning out resonance is not necessary in view of not

great grows of the vibration amplitudes.

The recommendations on the dynamical computations with optimization are

given in [1, 2]. As for the dynamical computations in whole, the basic problem is

to find the dynamical system characteristics in such way, that to exclude the tray

service at the resonance regimes taking into account the longevity constraints. It is

also important to achieve even distribution of the vibration amplitudes along the

surface of the tray at the expense of rational placement of the vibroexciters.

Note the one important speciality of obtained solutions. Since, the value

P is

normalized, the value

(eigenvalue of free loading structure) is found using the

frequency equations. It is seen from fig. 4 that this value can be defined by chang-

ing the values

D , l ,

C ,

The steel intensity of the cell (form) will be different for each case. The analy-

sis of the equations (28) and (29) shows that the minimal value of the steel inten-

sity is reached at the maximal values for

k . So, it is necessary to tend to the

following values for parameter

C : for shock and vibration machines –

300C ≥ ;

for shock machines –

C →∞; for vibration machines –

5C ≤ .Up to now all ele-

ments of FFM are designed separately. It can lead to unexpected phenomena:

•

exploitation of the tray forms in resonance regimes due to a compact spectrum

of the eigenfrequencies;

•

irregularity in the distribution of the vibration amplitudes along the surface;

•

necessity to grow shock actions on the forms and to increase its steel intensity.

The engineering methodic for dynamical computations with optimization of the

process, the laboratory and full-scale experience of application of the form with

improved dynamics parameters are given in [1, 2].

3 Conclusion

The realized complex of theoretic and experimental researches, including the iden-

tification of the structural and mechanical characteristics of the viscoelastic media