Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 109

Table 1 gives values of

≡λ

, of λ

and of λ

slightly smaller than

for various values of the stiffness and mass ratio k and m, respectively, together

with the corresponding final amplitudes θ

(τ) of the stable limit cycles. Note

that θ

(τ) increases with the increase of k and m. Fig.5 shows the phase-plane por-

trait θ



corresponding to the above generic Hopf bifurcation with k=10,

m=46.838455646 and λ

=0.898<λ

=0.9009805. Note that the (absolutely) maxi-

mum

amplitude of θ

(τ) corresponding to this generic Hopf bifurcation, is nearly

0.008 rad. The

maximum (absolutely) amplitudes of θ

(τ) are, as expected, lower

than the corresponding |maxθ

(τ)|.

Liénard-Chipard Stability Criterion

Subsequently we will discuss the effect of violation of the above stability criterion

for λ≠0 and λ=0.

The characteristic (secular) equation is

+α

ρ+α

= 0 (63)

where

()

.VVV

,c2VVcVc

,cm2VVmVm

c2mcmcm

1222114

1212112222113

1212112222112

1212112222111

−=

−+=

+−+=

−+=

(64)

where |c| = detC.

Let us first examine the effect of

violation of the Liénard-Chipart criterion on

the system stability in the case of

zero loading (i.e., λ= 0). Then eqs(64) due to

relations (54) are written as follows:

()

[]

()

[]

,2c1kcc

,ccc4mk

2cccm1

1222113

1222112

1211221

−++=

++++=

−++=

(65)

According to Liénard-Chipart criterion inequalities (41a) imply

> 0, α

> 0, Δ

>0, Δ

> 0, (66)

110 A.N. Kounadis

where Δ

= α

>0 and Δ

=α

(α

-α

>0. Clearly, from the last inequality, it

follows that α

> 0.

For c

>0 (i=1, 2), k>0 and m>0 (implying α

>0), it is deduced that this criterion

is violated if either one of α

or α

is zero or Δ

is zero. These three cases will be

discussed separately in connection with the algebraic structure of the damping

matrix

C=[c

Case 1 (α

= 0 with α

>0)

If α

= 0 (yielding Δ

=−

< 0), then

(1+m)c

-2c

= 0 (67)

Eq.(67), being independent of λ and k, is satisfied only when the damping matrix

C is indefinite, that is,

<0 (c

>0 for i,j=1,2) .

(68)

Indeed, the last inequality due to relation (67) implies

(1+m)

+2(m-1)c

(69)

which is always satisfied, regardless of the value of c

, since for m>0, the

discriminant of eq.(69) (equal to −16m) is always negative.

Thus, we have explored the

unexpected finding that an unloaded (stable) struc-

tural system (λ=0) becomes dynamically

unstable at any small disturbance in case

of an

indefinite damping matrix even when infinitesimal damping is included.

If all coefficients of eq.(63) are

positive from the theory of algebraic equations

it follows that this equation

cannot have positive root. Also the case of existence

of a pair of pure imaginary roots associated with Δ

=0 is ruled out, since Δ

(due to α

=0). Hence, eq.(63) has either two negative roots combined with a pair

of complex conjugate roots with

positive real part or two pairs of complex conju-

gate

roots with opposite real parts. Both cases imply local dynamic instability.

Case 2 (α

= 0 with α

>0)

If α

=0 (implying also Δ

< 0), then

04mkc <−−−=

(k, m >0).

(70)

Namely, the damping matrix [c

] is indefinite but with a large negative determi-

nant (rather unrealistic case). Since the Liénard-Chipart criterion is violated, the

model is again locally dynamically unstable.

The observation mentioned above at the end of

Case 1 is also valid for Case 2.

Namely, we have again

local dynamic asymptotic instability.

Case 3 (Δ

= 0)

In this case, stability conditions in eq.(66) are satisfied except for the last one,

since Δ

= 0 which yields

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 111

= α

(α

– α

) –

= 0

(71)

Note that λ<

implies α

>0 (i.e., detV > 0).

This is a

necessary condition for the secular eq.(63) to have one pair of pure

imaginary

roots ρ=±μi. Indeed, this can be readily established by inserting ρ=±μi

into eq.(63) and then equating to zero

real and imaginary parts.

Consider now the more general case of

nonzero loading (i.e. λ≠ 0). Using rela-

tions (64), eq.(71) can be written as follows

A λ

+Β λ+Γ = 0

(72)

where

()

[]

121122

221112211

2cccm1)cm(cα2))(mc(cA −++−+−++=

(73a)

()

[]

{}

c4mk)c(c2cc1kc2)(mĮB

22111222111

++++++++−=

()

[]

()()

[]

1211222211122211

2cccm12k)c(c2cc1kc2m −+++++++++

(73b)

[]

()

[]

()

[]

1222111122211

2cc1kcmα2cc1kcc4mkΓ +++−++++++=

−

()

[]

121122

2cccm1k ++−

(73c)

where

= (

+|c|)/ c

=mα

(73d)

For real λ, the discriminant

D of eq.(72) must be greater than or equal to zero, that

is,

D = B

− 4AΓ ≥ 0. (74)

Subsequently, attention is focused on the following: (a) matrix

C is positive semi-

definite (i.e., |c| = 0 with c

>0, i=1, 2) and (b) matrix C is indefinite (|c| < 0 with c

> 0, i =1, 2).

Using the

symbolic manipulation of Mathematica [24], one can find that

D = |c|f(|c|) (75)

where f(|c|) is an algebraic polynomial of 5th degree in |c|.

Case 4 (|c|=0, f ≠0)

For |c|=0, eq.(72) implying

D=0 admits a double root, which due to (73a),

(73b), (73c), (73d) is given by

()( )

mcccc

2mkcmkcc2c

2212

222212

−−

++−−+

(76)

Using the

Reduce Command embedded in Mathematica, one can find the condi-

tions under which, 0 <

, given in the appendix of ref [18].

112 A.N. Kounadis

Case 5 (f = 0, |c|≠0)

Moreover, it was found

symbolically that the 5th degree polynomial f(|c|) pos-

sesses

three real roots (one double and one single) and two pure imaginary ones.

Discussing their nature, one can find that the double root of f(|c|), being equal to

|c| = −(c

−c

)

−

m<0, yields

()

[]

221112

c1mc

c ++=

(77)

Then, the double root of eq.(72) becomes

()

2211

2mkc2c

+++

(78)

which is always

greater than

and hence of minor importance for the present

analysis.

The

third real root of f(|c|), if substituted in eq.(72), yields again a double root

in λ, always less than zero, which is rejected. Thus, only the case of a positive

semi-definite damping matrix may lead to an

acceptable value of the correspond-

ing load (i.e., 0<λ

) associated with a degenerate Hopf bifurcation as theo-

retically was shown by Kounadis [4, 13].

Case 6 (λ = 0)

If λ=0, eq.(72) implies Γ=0, which after symbolic manipulation of eq.(73c) can

be written in the following form

()

0AcAcAc

=+++=

(79)

where A

(i = 0, 1, 2) are given in the appendix of ref.[18] . It is evident that A

and A

≥0, a fact implying that eq.(79) can be satisfied only for |c| ≤ 0 if also A

≥0;

otherwise (i.e., if A

<0) the system may be dynamically locally stable or unstable.

For |c|=0, one can find the corresponding values of c

(i = 1, 2), given in the appendix

of ref. [18] which are always positive. This

special case, for which the trivial

(unloaded) state is associated with a pair of

pure imaginary eigenvalues (necessary

condition for a Hopf bifurcation) implies local dynamic asymptotic instability.

Conditions for a double imaginary root

For a double imaginary root the first derivative of the secular eq.(63) must be also

zero which yields

4ρ

+3α

+2α

+α

= 0. (80)

Inserting into eq.(80) ρ = μi, we obtain μ

= 0.5α

= α

/3α

and thus α

=3α

/2.

Introducing this expression of α

into eq.(71), it follows that α

=0, which also im-

plies that α

=0 and hence eq.(80) becomes ρ

= −0.5α

. If ρ

= −0.5α

is inserted

into the secular equation ρ

+α

= 0, for a double imaginary root, it follows

that α

−4α

= 0 which due to relations (64) yields

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 113

()

() ( )

()

222

cc2m82kmk2m2λλ4m +++++−+−+

()()

04mk4mkc4mk2

=−++++++

(81)

For

real λ, the discriminant D of eq.(81) must satisfy the inequality

()()

0kmcmk4c

≥+−−+=D

(82)

which yields

either

()

164k4km4mk0.5c

222

+++−−<

()

164k4km4mk0.5c

222

++++−>

(83)

Using the conditions found above

= α

= 0, (84)

relations (65) yield

()

() ( )

0.2cλ1kcλ1c

0,2cccm1

122211

121122

=+−++−

=−++

(85)

Adding the last two equations, we obtain

(2 - λ) c

+ (k + m + 2 - λ) c

= 0. (86)

Since k, m>0, and λ<

<1, it follows that both coefficients of c

and c

eq.(86) are

positive. Hence, c

and c

are of opposite sign (i.e., c

<0) and

consequently |c|=c

−

<0; thus the 2nd of inequalities (83) is excluded.

Solving simultaneously the system of equations α

−4α

=0, α

=α

=0 in k, m, λ,

two ternaries of values for k, m, and λ are obtained, given in the appendix of ref.

[18].

For all these values to be greater than zero, the

Reduce Command embedded in

Mathematica [24] yields two sets of conditions, given also in the appendix of ref.

[18]. Further symbolic computations are needed for establishing the conditions for

double pure imaginary root for loading values less than

. Nevertheless, suit-

able combinations of values of c

, k, and m may be found. The corresponding dy-

namic response, since the system is associated with a codimension-2 local bifurca-

tion, is anticipated to be related to isolated

periodic orbits which will be estab-

lished via a straightforward complete

nonlinear dynamic analysis.

Subsequently, numerical results corresponding to all the above cases of

viola-

tion

of the Liénard-Chipart stability criterion are given below in graphical and

tabular forms.

Case 1 (α

= 0)

(a) λ=0. For an unloaded system with k = m = 1, choosing c

= 0.015 and

= 0.002, eq.(67) yields c

= 0.0095 and as expected the damping matrix is

indefinite with determinant |c| = −0.0006025. The two pairs of corresponding

114 A.N. Kounadis

eigenvalues are ρ

1,2

= −0.00332577±0.41421i and ρ

3,4

= 0.00335877±0.41421i

(i=√−1), implying local dynamic instability. Solving numerically the system of

nonlinear equations of motion (52), we find that the dynamic response of the sys-

tem is associated with a

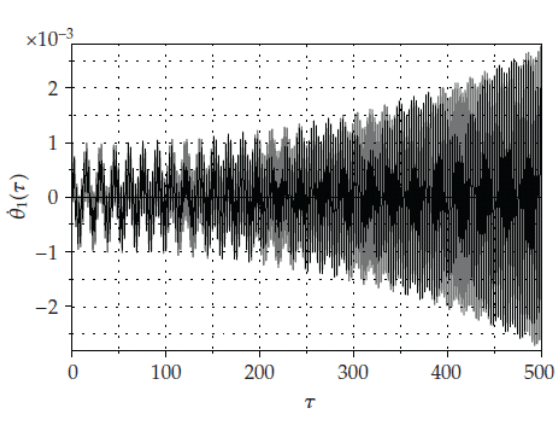
divergent (unbounded) motion, as depicted in Fig.6 with

the aid of the plot angular velocities



(τ) versus time τ.

Fig. 6. Angular velocities



(τ) versus time τ.

(b) λ≠0. For a system with k=5, m=4, and λ=0.5<

=0.807418 and for

=0.01, c

=0.005, eq.(67) yields c

=−0.0175 implying |c|=−2.5625×10

−4

. The

trivial state is locally dynamically unstable, since ρ

1,2

=−0.00397748±0.4351i and

3,4

=0.00397748±0.4351i. The corresponding dynamic response is again related to

divergent (unbounded) motion.

Case 2 (α

= 0)

(a) λ = 0: If k=m=1 relation (70) is satisfied, for example, for the damping coeffi-

cients c

= 0.50, c

= 2.00, yielding c

= √7 and |c| = −6. For this, rather unrealistic

subcase, the corresponding eigenvalues are equal to ρ

= −1.86617, ρ

= −0.102227,

and ρ

3,4

= 1.37995 ± 1.8269i (local instability). Hence, the response of the system is

also related to a divergent (unbounded) motion, presented graphically in the

phase-plane portrait of Fig. 7(a,b).

(b) λ≠0. Similarly, for a system with k=0.10, m=0.20 (for which

= 0.0487508)

in order that α

= 0, we must choose an indefinite damping matrix with |c| = −4.25.

Setting, for example, c

= 2.375, c

= 3.00, c

= 2.00, and λ = 0.227273 <

, the

trivial state is locally dynamically unstable with ρ

= −2.46657, ρ

= −0.00503929,

and ρ

3,4

= 4.2983 ± 1.6612i. The system exhibits again a divergent (unbounded)

motion [18].

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 115

(a)

(b)

Fig. 7a, b. Phase-plane portraits [θ

(τ),



(τ)] (i=1,2) for the system of Case 2(a), associated

with a divergant motion.

Case 3 (Δ

=0 with α

≠0)

(a) Positive semi-definite damping matrix

C (|c| = 0).

Choosing c

= 0.01, c

= 0.0004 (and thus c

= 0.002), the 1st requirement of the

2nd set of conditions given in the appendix of ref. [18] is satisfied (i.e., c

> c

The 2nd requirement, that is m > 2(c

−c

)/c

, yields m > 8, and hence one can

choose m=10. The 3rd requirement given in the appendix of ref. [18] implies that

0.8333<k<3 and thus one can take k=1. Solving numerically eq.(71) with respect

to λ, we obtain the value of λ

= 0.307692256 <

= 0.381966 associated with a

pair of

pure imaginary eigenvalues, while the other pair has negative real parts.

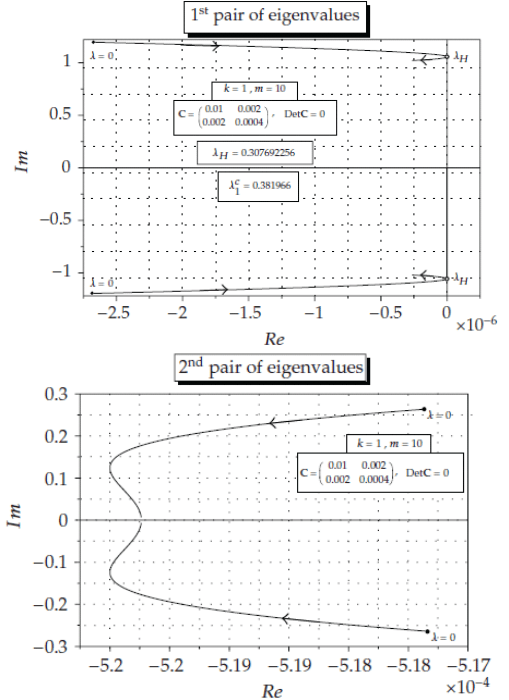
116 A.N. Kounadis

The evolution of both pairs of eigenvalues in the complex plane as λ varies is

presented in Fig.8(a,b) for λ<

. For λ=λ

, a degenerate Hopf bifurcation occurs

and the system exhibits a

periodic motion, whose final amplitude depends on the

initial conditions. Relevant results in graphical form can also be found in recent

publications [4, 13].

(b) Indefinite damping matrix

C (|c| < 0).

It has been proven by Kounadis [4, 13] that in this subcase (for λ<

) all the

necessary and sufficient conditions for a generic Hopf bifurcation are fulfilled and

hence the system experiences a periodic

attractor response (stable limit cycles)

with constant final amplitudes, regardless of the initial conditions.

(a)

(b)

Fig. 8 a, b. Evolution of both eigenvalues in the p-complex plane for the system of Case3(a)

associated with a degenerate Hopf bifurcation.

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 117

= 0 and λ = 0.

If at the same time |c|=0, one can find the values of c

= (i = 1, 2) given in the

appendix of ref.[18] which are always positive. A further investigation of this case

as well as of the case |c|<0 for the

global stability of the system can be performed

through a

nonlinear dynamic analysis.

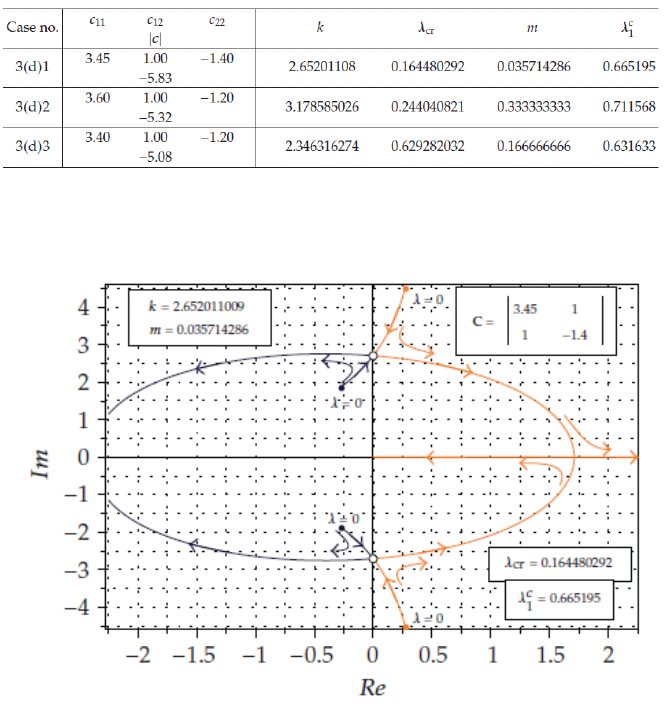
(d) Double pure imaginary eigenvalues

For this special case, three combinations of damping matrix coefficients c

are

examined. These, along with the corresponding critical values of k, λ and m, satis-

fying the appropriate relations given in the appendix of ref.[18], are presented in

Table 2.

Table 2. Values of the damping coefficients (c

) and critical system parameters (k, λ

, m)

for three subcases with double pure imaginary eigenvalues.

In the three above subcases, the evolution of both pairs of λ-dependent eigen-

values in the ρ-complex plane is depicted in Figs 9, 10, 11(a) and 11(b), from

Fig. 9. Evolution of both pairs of eigenvalues in the ρ-complex plane for the system of Case

3(d)1.

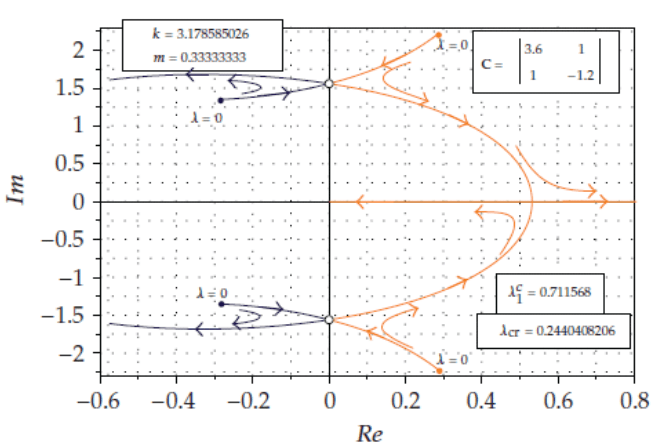
118 A.N. Kounadis

Fig. 10. Evolution of both pairs of eigenvalues in the ρ-complex plane for the system of

Case 3(d)2.

which it is evident that for all λ<

, except for λ<λ

(where a codimension-2 bi-

furcation occurs), the pairs of eigenvalues remain always in

opposite planes of the

Im axis, but symmetric with respect to the Re axis. This symmetry is always pre-

sent for the pair with negative real parts, while for the other pair (with positive real

parts), this feature remains until their imaginary part vanishes simultaneously at a

certain value of the loading λ

less than

The dynamic response of the system for all these subcases is associated with

isolated

periodic orbits (whose final amplitude is constant and independent of

the initial conditions). A relative phase-plane portrait is shown in Fig.12a,b The

corresponding dynamic bifurcations related to the above

double pure imaginary

eigenvalues behave like a generic Hopf bifurcation, whose basic feature is the

intersection of the λ-dependent path of one eigenvalue with the imaginary axis.

On the other hand, in all the above subcases, the branches of two consecutive λ-

dependent eigenvalues meet the imaginary axis at the same point with λ=λ

Namely, the

transversality condition is satisfied through two intersected lines at

the same point of the imaginary axis, but whose branches in the left (negative)

and right (positive) half planes belong to the 1st and 2nd pairs of eigenvalues,

respectively.