Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 119

(a)

(b)

Fig. 11. (a) Evolution of both pairs of eigenvalues in the ρ-complex plane and (b) corre-

sponding detail for the system of Case 3(d)3.

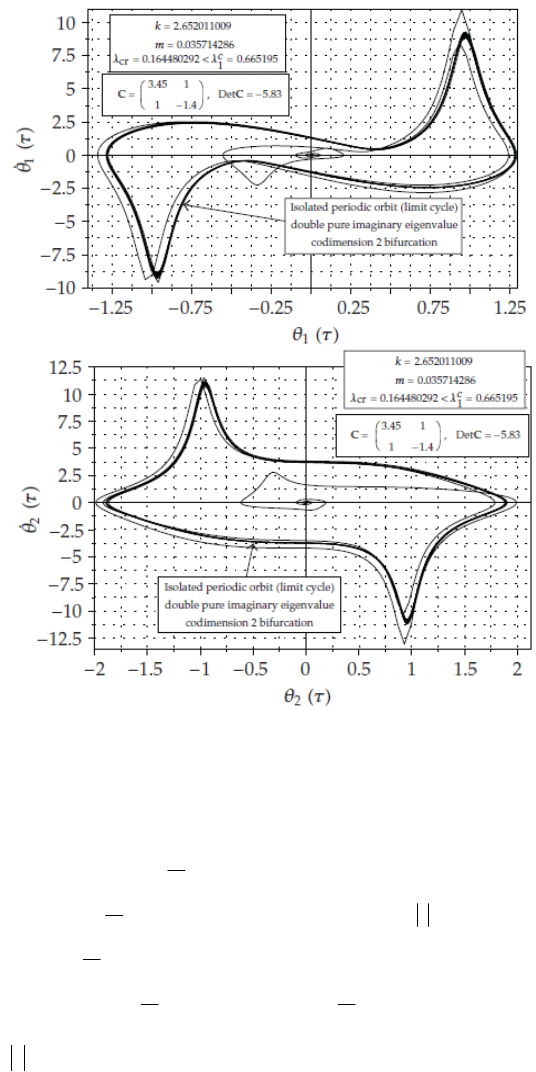
120 A.N. Kounadis

(a)

(b)

Fig. 12. Phase-plane portraits [θ

(τ),



(τ)] (i=1,2) for the system of Case 3(d)1, associated

with an isolated periodic orbit.

5.2 Non Conservative Systems (η≠1)

In this case the coefficients of the secular equation(63) α

=(1,2,3,4) are

[]

{}

[]

⎪

⎭

⎪

⎬

⎫

=+λ+η−ηλ=α

−ηλ++λ−++λη−=α

+−ηλ+λ−++λη−+=α

−++=α

Vdet

k)2k(

c)]1(2[)k1(c)1(c

c)1(k3)1)(m1(

c2cc)m1(

1222113

1211221

(87)

where

.Cdetc =

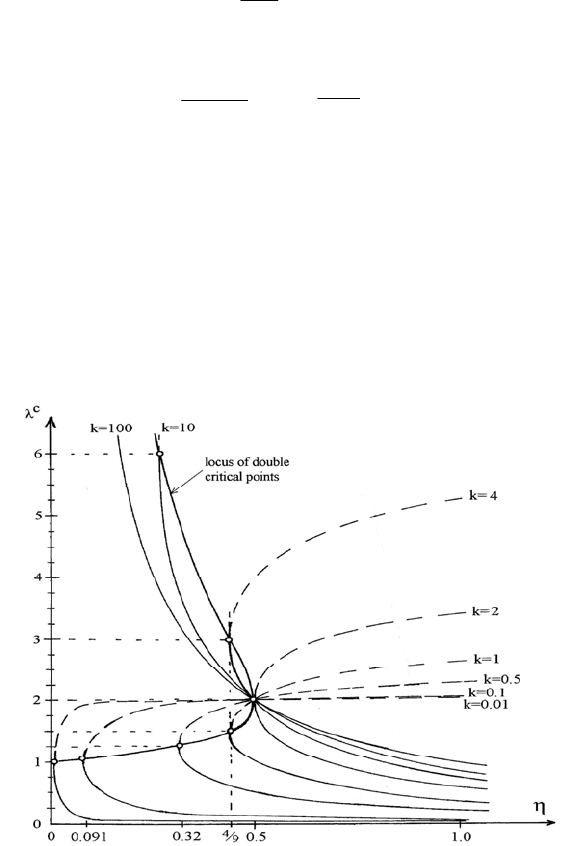
Extreme Instability Phenomena in Autonomous Weakly Damped Systems 121

The region of existence of adjacent equilibria (region of divergence instability)

is related to static bifurcations with two

distinct critical loads obtained via α

=0 or

eq.(55). The

boundary between the region of existence and non-existence of adja-

cent equilibria is defined by (see also eq.(3))

=α

(88)

which due to relations (87) gives (see eq.(56))

)2k(

=η

=λ

(89)

This is a

double (compound) branching point related to a double root of eq.(55)

with respect to

λ. Considering the function η=η(λ, k) the necessary condition for an

extremum,

0k// =∂η∂=λ∂

∂

, yields λ

=2 and k

=2 implying η

.=0.5 Note that

is the maximum distance

of the double branching point from the λ

-axis (curve η

).Two characteristic cases are considered for k<2 and k>2. It is clear that

→λ

and η

→0 as k→0, whereas k>2 yields

∞→λ

, η

→0 as k→∞.It is easy

now to establish the

locus of the double branching points in the plane of η versus λ

(Fig.13), being independent of m . Note that for k→0 or k→∞ the region of flutter

instability

disappears.

Fig. 13. Locus of double branching points (

,ηλ

122 A.N. Kounadis

Subsequently, the Linéard-Chipart criterion for

asymptotic stability is used

which is more simple and efficient than that of Routh-Hurwitz. Clearly, if one of

the conditions (41

α,b) is violated there is no asymptotic stability. We will apply

this criterion for the above 2-DOF cantilevered model (n = 4,

= 1) in case of a

positive definite damping matrix for which one can show that m>0 always implies

>o. Let us now consider the case of the Rayleigh positive definite viscous damp-

ing matrix in the region of

divergence (static) stability, i.e. for η ≥ η

= 4k/(k+2)

Then since c

= c

, c

= c

= -c

and c

= c

> 0, i=1,2) relations (87) become

[]

211

m)c(4c

α ++=

[]

)2m(cc4km

212

+ηλ−+++=α

[]

)2k(c)1(c

213

λη−+λη−=α

[]

k)2k(

+λ+η−ηλ=α

(90)

According to the 1

set of conditions (41a) we have

>0, α

>0, Δ

= α

>0, Δ

>0 (91)

where

13213

)(

αα−α−ααα=

αα

=Δ

(92)

From eqs(90) it follows that

>0. Since α

=det(V/m) (m>0) one may consider the

following cases regarding the interval of variation of

For

0Vdet

>⇒λ<λ

and hence α

For

0Vdet

<⇒λ<λ<λ

and hence α

<0 (93)

For

0Vdet

>⇒λ≥λ

and hence α

>0.

Considering always the region of

divergence (static) instability [i.e.

)2k/(k4 +≥η

]

and in connection with above interval of values of

λ the following cases of violation

of conditions (91) are discussed below:

case: α

>0 (for λ

0),

<αλ<

, Δ

>0.

Due to eq.(92), clearly

>0 implies α

<0 (since always

) or due to rela-

tion (90)

(1-λη) + c

(k-2λη) <0. (94)

Since c

, c

>0 the quantities 1- λη and k-2λη must be of opposite sign.

Inequality (94) can always be satisfied for suitable values of c

> 0 (i=1, 2). Subse-

quently one can find suitable values for k,

η and m for which

=λ<λ

⎥

⎦

⎤

⎢

⎣

⎡

η−+−+ /k4)2k(2k5.0

is also consistent with

<0 The important conclu-

sion

which then can be drawn is that a local dynamic asymptotic instability in

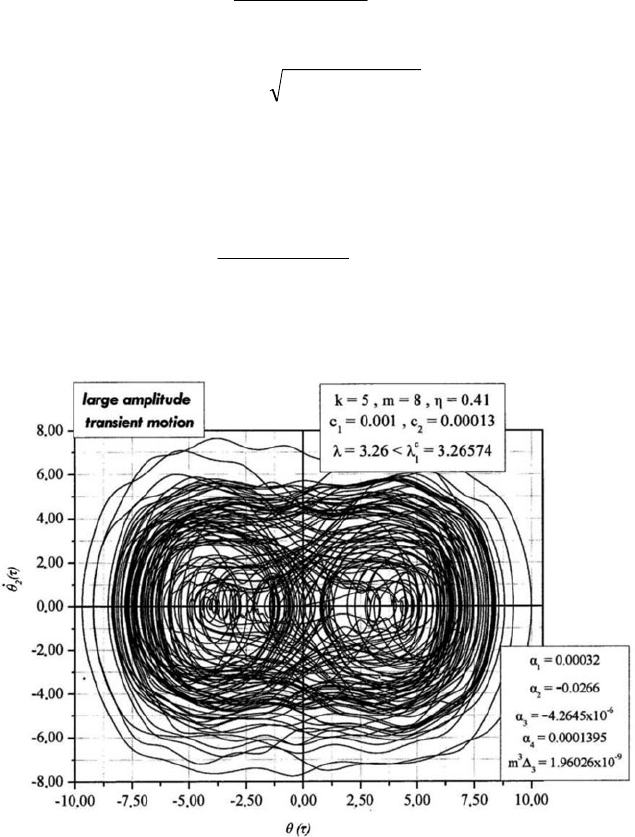
Extreme Instability Phenomena in Autonomous Weakly Damped Systems 123

regions of

divergence (for λ less than the 1

buckling load) may occur in case of a

positive definite damping matrix. This is excluded in case of a conservative loading

(

η=1) as was shown recently by Kounadis [4, 13].

More specifically one can establish to the following proof:

Condition

<0 due two relations (90) implies

cc4km

+η

+++

>λ

(95)

which must be consistent with eq.(56), i.e.

<λ

⎥

⎦

⎤

⎢

⎣

⎡

η−+−+ /k4)2k(2k5.0

(96)

One can show that there are values of

λ for which both inequalities (95) and (96)

are satisfied for

η ≥ 4k/(k+2)

, m>0, k>0 and c

>0 (i=1,2). For example for k=5,

m=8, c

= 0.001 and c

= 0.00013 we get η≥4k/(k+2)

= 20/49 = 0.408163265.

Choosing

η=0.41 we obtain

= 3.26574, as well as

219697.3

cc4km

+η

+++

>λ

For

,26574.326.3

=λ<=λ

we find: α

= 0.00032, α

= -0.0266, α

= -4.26x10

-6

= 0.0001395 and m

= 1.96x10

-9

≈0 . Fig. 14 using these values of parameters α

Fig. 14. Phase-plane response [θ

(τ),



(τ)] for a cantilever with k=5, η=0.41, m=8,

=0.001, c

=0.00013 and λ=3.26<

26574.3

=λ

. The model is locally dynamically un-

stable exhibiting a large amplitude chaoticlike motion.

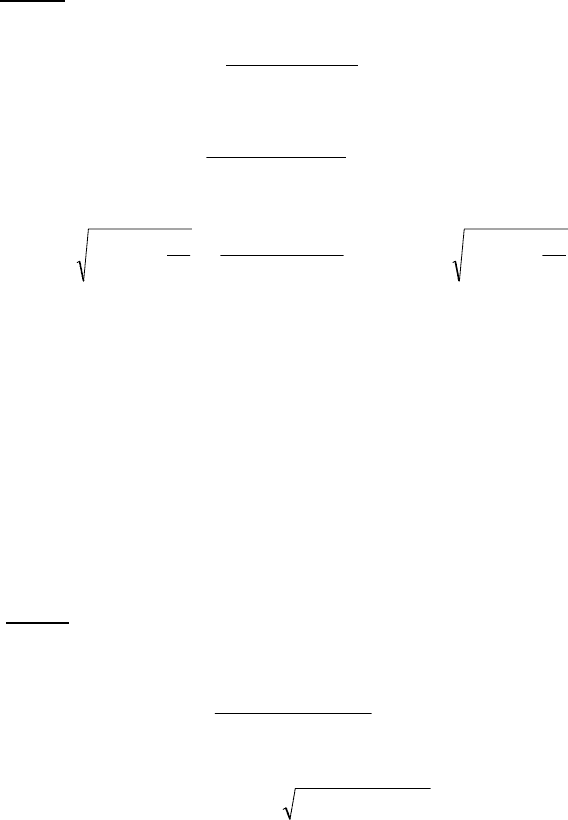
124 A.N. Kounadis

(i = 1,...,4) shows a large amplitude

chaoticlike response in the phase-plane portrait

[

(τ) vs



(τ)]. Hence, for 3.26 ≤ λ ≤3.26574 the damped autonomous system

exhibits

local asymptotic instability before divergence for a positive definite

damping matrix (with coefficients practically zero) of the Rayleigh viscous type.

This is an

unexpected finding which does not occur for the same system under

conservative (η=1) load [4, 13].

case: α

<0 (for

)

λ<λ<λ

, α

>0, Δ

>0.

By virtue of relations (90) the condition

>0 implies

cc4km

+η

+++

<λ

(97)

and hence

cc4km

λ<

+η

+++

<λ

(98)

or due to eq.(55)

⎥

⎦

⎤

⎢

⎣

⎡

−+++<

+++

⎥

⎦

⎤

⎢

⎣

⎡

−+−+

2)(k2k0.5

2ηm

cc4km

2)(k2k0.5

(99)

For instance, if k = 10, then

η≥4k/

2777777.0)2k(

. Choosing η=0.41,

= c

= 0.001 and m = 7.5 inequality (99) yields 2.59269<4.23645 <9.40731.

For

λ=3 we get: α

=0.001667, α

=0.83667, α

=0.00097467, α

=-0.142667 and

=3.39795x10

-4

As was anticipated the system is locally dynamically asymptotically unstable.

However, a

nonlinear dynamic analysis will show that the system is globally sta-

ble. This is so, because the cantilever under

statically applied load exhibits post-

buckling strength

and hence the postbuckling stable equilibria act as point attrac-

tors

. Fig.15 shows the corresponding to the above parameters α

(i=1,…,4) motion

in the phase-plane portrait

)([

τθ



)](τ

which after large amplitude chaoti-

clike vibrations is finally

captured by the left stable equilibrium point (of the can-

tilever) acting as

point attractor.

case: α

>0 (for

λ>λ

<α

>0.

Apparently

<0 and Δ

>0 imply α

<0. Inequality α

<0due to relations (90)

yields

cc4mk

+η

+++

>λ

(100)

On the other hand we must also have

⎥

⎦

⎤

⎢

⎣

⎡

η−+++=λ>λ /k4)2k(2k5.0

(101)

One can readily show that both inequalities (100) and (101) can be satisfied for vari-

ous values of

λ and of the parameters m>0, k>0, c

>0 (i=1,2) and η

)2k/(k4 +≥

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 125

Fig. 15. Phase-plane response [θ

(τ),



(τ)] for a cantilever with k=10, η=0.41, m=7.5,

=0.001and

=λ

2.59269<λ=3<

=9.40731. The model exhibits a large amplitude

chaoticlike motion which finally is captured by the left stable equilibrium point acting as

point attractor.

For instance, for m = 4, c

= 0.001, c

= 0.003 and k=1 implying η= 4/9, after

choosing

η = 0.45 we obtain λ≥(k+m+4+c

)/(ηm+2) = 2.36842 and

.66666.1

=λ

Hence, for

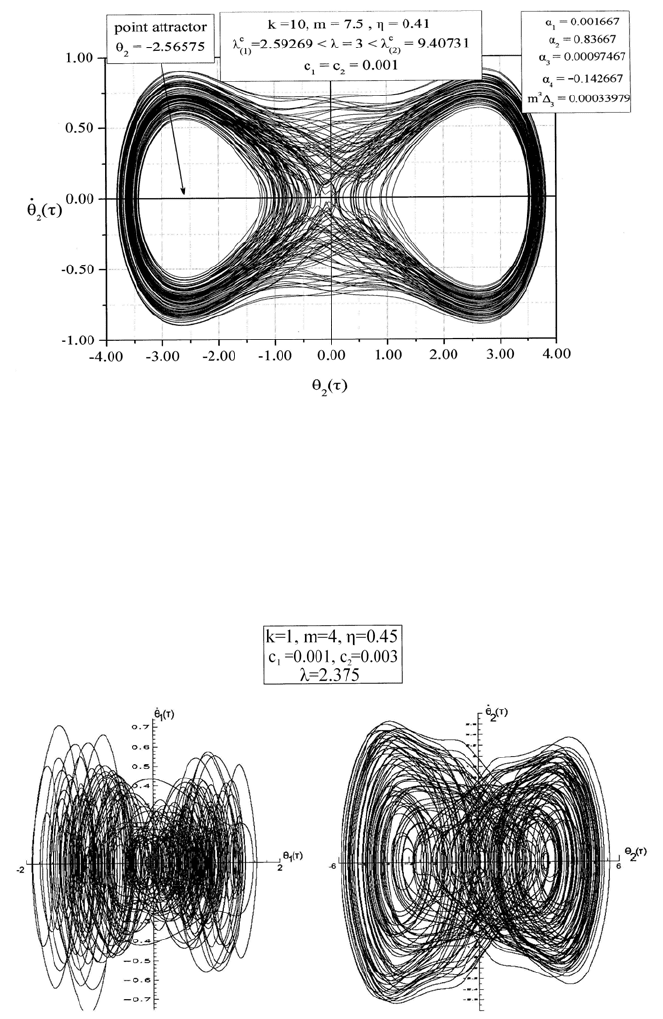
λ = 2.375 we have local asymptotic instability. Fig.16 shows the

Fig. 16. Phase-plane responses [θ

(τ),



(τ), i=1,2] for a cantilever with k=1, η=0.45, m=4,

=0.001, c

=0.003 and λ=2.37>(k+m+4+c

)/(ηm+2)= 2.36842.

126 A.N. Kounadis

corresponding to these values of the parameters phase-plane responses [

(τ) vs



(τ), i= 1,2].

4th case

: α

> 0 for

λ<λ

, α

> 0, Δ

≤ 0

The condition

= 0 (being necessary for a Hopf bifurcation) yields

13213

)( αα−α−ααα

= 0 (102)

which due to

> 0 implies also α

> 0. (103)

For instance, if k=1 then

)2k/(k4 +=η

=4/9. Subsequently choosing η=0.45 we

obtain

⎥

⎦

⎤

⎢

⎣

⎡

η−+−+=λ /k4)2k(2k5.0

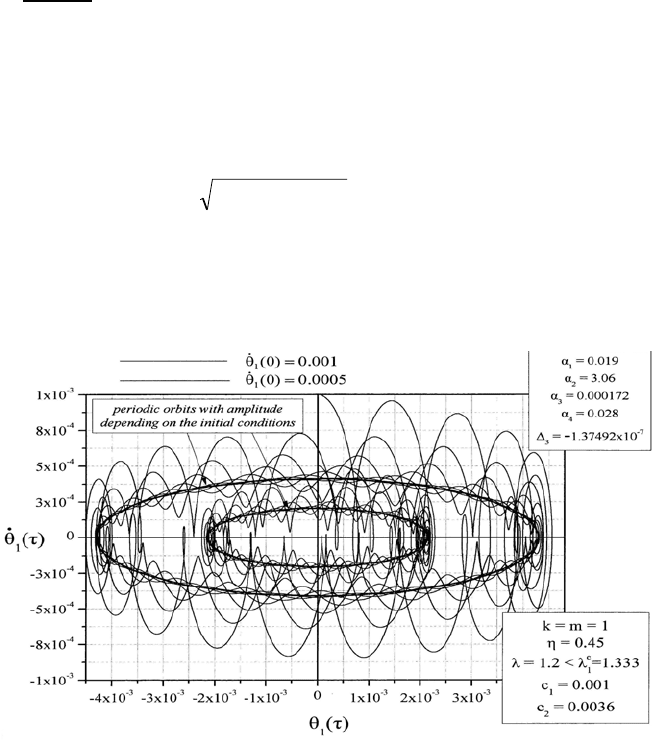
=1.3333. Let us take λ=1.2, m=1,

= 0.001and c

= 0.0036 which yield: α

= 0.019, α

= 3.06, α

= 0.000172,

= 0.028 and Δ

=-1.3749x10

-7

. On the basis of these values of parameters

(i=1,...,4) Fig.17 shows periodic motion around centers in the phase-plane por-

trait [

(τ),



(τ)], whose final amplitude depends on the initial conditions.

Fig. 17. Phase-plane response [θ

(τ),



(τ)] for a cantilever with k=1, η=0.45, m=1,

=0.001, c

=0.0036 and

33333.12.1

=λ<=λ

. The model is locally dynamically un-

stable exhibiting periodic motion around centers, whose final amplitude depends on the

initial conditions.

Eq.(102) is the necessary condition for the existence of a pair of purely imagi-

nary

roots of the characteristic eq.(63). Τhis case is associated either with a de-

generate

Hopf bifurcation or with a generic Hopf bifurcation [4, 13].

Extreme Instability Phenomena in Autonomous Weakly Damped Systems 127

Using relations (87), eq.(102) reduces to the following 2

degree algebraic

equation with respect to

Αλ

+Βλ+Γ = 0 (104)

where

A=m[

ηc

−c

(η−1)]

+η[(1+m)c

−2c

]

−(

ηm+2)[(1+m)c

−2c

][ηc

−c

(η−1)]

B=[(1+m)c

−2c

]{(ηm+2)[c

(1+k)+2c

]+(4m+k+|c|)[ηc

−c

(η−1)]}

−2m[ c

(1+k)+2c

][ηc

−c

(η−1)]−η(k+2)[(1+m)c

−2c

]

Γ=m[ c

(1+k)+2c

]

+k[(1+m)c

−2c

]

−[(1+m)c

−2c

] (4m+k+|c|)[c

(1+k)+2c

] (105)

Note that contrary to A and B, the coefficient

Γ is independent of η.

For

real λ the discriminant D of eq.(104) must satisfy the inequality

D = B

-4ΑΓ 0≥ .

(106)

Three characteristic cases are related to eq.(104): (a) D>0 [two unequal roots of

eq.(104)], (b) D=0 [two equal roots:

]A2/B−=λ

and (c) λ=0 implying Γ=0.

Note also that the intersection between the curve of eq.(102) and the curve of the

static load λ

, corresponds to a dynamic coupled flutter-divergence bifurcation.

Conditions for a double imaginary root

For a

double imaginary root the first derivative of the secular eq.(63) must also be

zero, which yields

0234

=α+ρα+ρα+ρ

(107)

Inserting into eq.(106)

)1i( −=

we obtain μ

= 0.5α

= α

/3α

and thus

= 1.5α

. Since ρ=μi must also be a root of eq.(63) we obtain μ

= α

/α

which

implies

= 0.5α

. This is consistent with the previous expression of α

= 1.5α

only when

= 0 due to either α

= 0 (which is excluded for a positive definite

damping matrix) or

= 0 (which is also excluded since it implies μ=0). Hence, if

the damping matrix C is positive definite of Rayleigh viscous type (i.e. c

=-c

and c

with c

both positive) then the case of a double imaginary

root is excluded.

6 Conclusions

The most important conclusions are:

• A thorough, comprehensive and readily employed technique was developed

for discussing the effect of the algebraic structure of the damping matrix in

connection with other parameters on the asymptotic stability of autonomous

weakly damped symmetric or asymmetric systems using mainly the more sim-

ple and efficient Liénard and Chipart stability criterion.

• The above systems under certain conditions may exhibit a dynamic mode of

instability due to: (a) an isolated degenerate Hopf bifurcation, (b) an isolated

128 A.N. Kounadis

generic Hopf bifurcation, (c) a double zero eigenvalue bifurcation and (d) a

purely double imaginary bifurcation.

• Unlike case (b) related to limit cycles, the global stability in cases (a), (c) and

(d) is due to periodic motion (around centers) not leading to limit cycles.

Conservative (symmetric) systems

• Degenerate Hopf bifurcations may occur for a positive semi-definite damp-

ing matrix and positive definite stiffness matrix; then the final amplitude of

resulting periodic motions depends on the initial conditions.

• Generic Hopf bifurcations (related to flutter mode of instability or periodic

attractors) may occur for an indefinite damping matrix. Generic and degener-

ate Hopf bifurcations may occur before divergence even in cases of infinitesi-

mal damping; a fact that may be important in applied engineering problems. In

this case, Zieglers’s kinetic (dynamic) criterion fails to predict the correct criti-

cal load.

• A double zero eigenvalue bifurcation associated with a coupled flutter-

divergence mode of instability may occur when both the damping and stiff-

ness matrix are positive semi-definite with a common real eigenvector.

• The eigenvector corresponding to an isolated degenerate Hopf bifurcation is

real, while that of a generic Hopf bifurcation is complex.

• In case of a positive eigenvalue the linearized analysis of the cantilevered model

leads to the

erroneous result of an unbounded motion, while a nonlinear analy-

sis shows that the long term response is associated with a point attractor.

Moreover, the existence of closed trajectories involving

saddle separatrices

passing through the origin may lead to a misleading conclusion. To avoid this,

one should also confirm the stability of postbuckling equlilibria via a nonlinear

static stability analysis.

• Infinitesimal damping combined with mass (mainly) and stiffness distribution

may lead to the unexpected result of discontinuity in the flutter load.

• The coupling effect on the dynamic critical (flutter) load of weak damping

with mass and stiffness distributions, as well as on the final (maximum) am-

plitude of the stable limit cycles, is also established.

• The cantilevered model when unloaded (being statically stable), strangely

enough, under certain conditions becomes dynamically

unstable to any small

disturbance leading to a

divergent (unbounded) motion.

• The above model when loaded under analogous of the previous conditions ex-

hibits also a

divergent motion at a certain value of the external load. It is worth

noting that the above cases of divergent motion may occur for

negligibly small

negative determinant of the damping (indefinite) matrix when α

=0, while for

=0 (regardless of whether λ = 0 or λ≠ 0), the determinant of the damping ma-

trix is negative but

finite.

• The case of a double pure imaginary eigenvalue may occur for an indefinite

damping matrix with finite determinant and negative ratio of the corresponding

diagonal elements. In this special case, there are

two pairs of eigenvalues in the

ρ-complex plane which touch the imaginary axis at the same point for a certain

value

λ=λ

. This situation yields local instability leading to a motion with final