Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Variational Approach to Static and Dynamic Elasticity Problems 149

(the power)





of energy (the power) includes a term

err



which shows the en-

ergy change rate caused by system discretization. It is follows from Eq. (62) that

the value of parasitic energy

err

Wdt

∫



is related to the value of the error Δ .

7 3D Beam Lateral Motions

As an example of algorithm implementation, let us consider the 3D problem of lat-

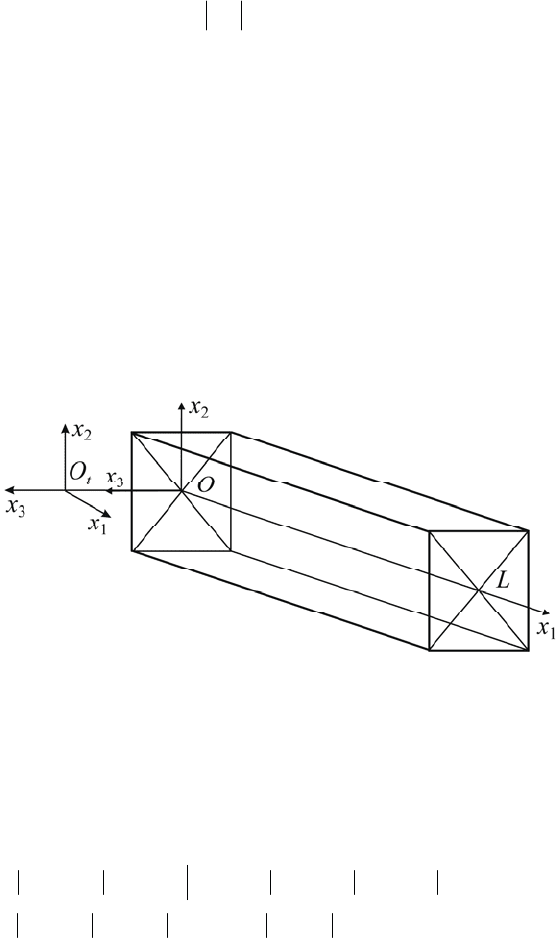
eral controlled motions for the rectilinear beam with a quadratic cross section (see

Fig. 1). The sizes of the cross section do not change along the beam length. It is

supposed that the volume forces are absent ( 0=f ) and the beam is made of ho-

mogeneous and isotropic material with given Young's modulus

, Poisson's ratio

, and volume density

. The geometrical beam parameters such as the beam

length

L and structural height 2a as well as terminal time are fixed, and hence the

problem is defined in the following 4D time-space domain

{

}

123123

{, : (0, ), }, , , :0 ,| | ,| | .tx t T x x x x x L x a x aΣ= ∈ ∈Ω Ω= < < < <

Fig. 1. Rectilinear elastic beam

Let us introduce the fixed reference frame

123

Ox x x . Its origin O coincides with

the central point of the left beam cross section in the initial time. The

x -axis is

directed along the beam and the coordinate axes

Ox and

Ox are parallel to the

cross section sides. The boundary conditions under consideration are

2 2 333

11 111

12 22 23 13 23 33

11 12 13 1 2

0, 0

xa xa

xa xa xa

xL xL x x

σσσσσσ

σσσ

=± =±

=± =± =±

=±

== ==

======

=== ==

(63)

150 G.V. Kostin and V.V. Saurin

The time-dependent polynomial displacement

u of the left beam cross section is

chosen as a control boundary function v :

uvvt

∑

(64)

where

N is a given integer defined the number of independent control parameters.

To find an approximate solution and optimize control in the problem of 3D lat-

eral beam dynamics a polynomial representation of the unknown functions was

used by Kostin and Saurin [17]. In [19] bivariate piece-wise polynomial splines

defined on rectangular meshes were applied to modeling and optimization of lat-

eral Bernoulli beam motions. In this example a finite element approach and spline

techniques are used to model 3D beam dynamics.

Let us consider the variational problem (57), fix an approximation order

M ,

and choose the following approximations

()



()



, , 1,2,3kl= , for unknown

components of displacement vector

u and the stress tensor σ

() ()

(, ) 2 2 1 (, ) 2 2 2 2 2 1 2 2

11 11 1 2 3 23 23 1 2 3 2 3

() ()

(,)22221 (,)22221

22 22 1 2 2 3 33 33 1 3 2 3

( , ) , ( , )( )( ) ,

( , )( ) , ( , )( )

p p

ij i j ij i j

ij ij

ij ij ij ij

ij ij

txxx txaxaxxx

tx a x xx tx a x xx

σσ σσ

−

+ −−

+= +=

==−−

=− =−

∑∑

∑



() ()

(, ) 2 2 2 1 2 1 (, ) 2 2 2 2

12 12 1 2 2 3 13 13 1 3 2 3

() ()

(, ) 2 2 1 (, ) 2 1 2 1

1112322123

()

( , )( ) , ( , )( ) ;

(, ) , (, ) ,

p p

ij i j ij i j

ij ij

ij i j ij i j

ij ij

tx a x x x tx a x x x

uutxxxuutxxx

σσ σσ

−

+= +=

−

+++

+= +=

=− =−

∑

∑∑





(, ) 2 2

123

(, ) .

ij i j

tx x x

∑

(65)

Here

(, )ij

u and

(, )ij

are functions of the time t and coordinate

x which will be

defined below. These approximations obey the boundary conditions on the beam

sides parallel to the

x -axis.

The symmetry with respect to coordinate planes

Ox x and

Ox x allows one to

decompose the original problems to four independent subproblems including 3D

beam compression-stretching, bending around

Ox axis, bending around

axis, and torsion. In this example the control displacement in (64) excites only

bending motions around

Ox axis. The polynomials with respect to the variables

x and

x proposed in Eq. (65) do not violate the symmetry properties of prob-

lem (57) under the boundary and initial conditions (63)–(65) as it has been shown

in [17].

Variational Approach to Static and Dynamic Elasticity Problems 151

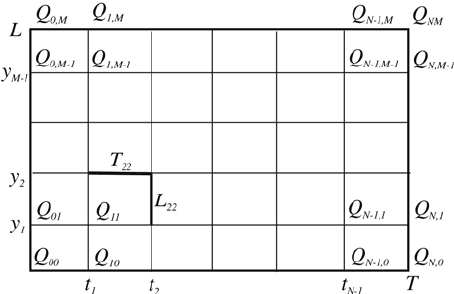
Fig. 2. Space-time mesh.

Divide the two-dimensional time-space domain

{, } (0, ) (0, )tx T L∈ϒ= × on

NM× rectangles

which vertices have coordinates

1, 1kl

−−

1,kl

−

,1kl

−

,kl

Q , where

{, }

kl k l

Qty= ;

1kk

−

> , 1, ,kN= … ;

1ll

−

> , 1, ,lM= … ;

0t = ,

tT= ,

0y = ,

yL= (see Fig. 2). Let also the boundary edges of these time-

space rectangles be named

(,)

kl k l kl

LQQ

−

= , 0, ,kN= … , 1, ,lM= … , and

(,)

kl k l kl

TQQ

−

= , 1, ,kN= … , 0, ,lM= … . In each 4D time-space subdomain

{

}

123 1 2 3

,,, :(,) ,| | ,|| .

kl kl

tx x x tx x a x aΣ= ∈ϒ < <

approximating polynomials

(, )ij

and

(, )ij

αβ

are given

23 0 23 011

01 01

(,) (,)

() ()

111 1

01 23 4 5

(, ) , (, ) , , 1,2,3;

{ }, 0, ,5; , , , , 0, , , 0, , .

jj j jj j

jjJJ

ipp

jj jj

u tx u tx tx tx

Jji jjN jjM j Nj M

α α αβ αβ

σσαβ

+= +=

===

== ≤ ≤ = =

∑∑

………

(66)

Here

()J

and

(,)jj

αβ

are unknown real coefficients. The integer

N is chosen so

that the equilibrium equation and zero initial conditions in Eq. (57), boundary condi-

tions (63), (64) can be exactly satisfied. In addition, to apply the variational formula-

tion given above the following conformed interelement relations must obey

() ( 1,)

123 123

() ( 1,)

123 123

() (,1)

23 23

()

{, } , 1, , 1, 1, , :

(, , , ) (, , , ),

(, , , ) (, , , );

{ , } , 1, , , 1, , 1 :

(, , , ) (, , , ),

kl k l

tx L k N l M

txxx txxx

tx T k N l M

ty x x ty x x

∈=−=

∈= = −

⋅

……



……





(, 1)

23 23

,,) (,,,), (1,0,0).

xx tyxx

=⋅ =nn



(67)

152 G.V. Kostin and V.V. Saurin

After satisfying local constraints in Eq. (57) and interelement conditions (67) the re-

sulted finite-dimensional unconstrained minimization problem yields an approxi-

mate solution ( , , )txv

∗



, ( , , )txv

∗



σ for arbitrary control parameters

v in (64).

8 Numerical Results

In this section the numerical results of 3D modeling for the lateral beam motions

described in the previous section are presented. For geometrical and mechanical

parameters the following dimensionless values have been chosen:

1, 0. 05, 2, 1, 1, 0.3, 4 , 4 / 3,La T SEI SaIa

ρν

== = = == = =

and the mesh and approximation numbers are assigned: = 5N ,

=1M , =2

M ,

=10

N . For numerical solution of this dynamical problem a time uniform mesh

with node instants = /

tiTN, 1, ,iN= … , is used. After satisfying equilibrium

equation, initial, boundary, and interelement conditions, the total number of de-

grees of freedom is equal to 1985

DOF

N = . The following function of lateral dis-

placement for the left beam cross section is fixed as a sample control law

(3 )/4, (0) (0) () 0, () 1.vtt vvvT vT=− = = = =



(68)

For the given system data the estimated value of the energy time integral is

0.1822Ψ= . The absolute and relative integral error defined in Eq. (62) are

0.0020Φ= ,

1.1%Δ= .

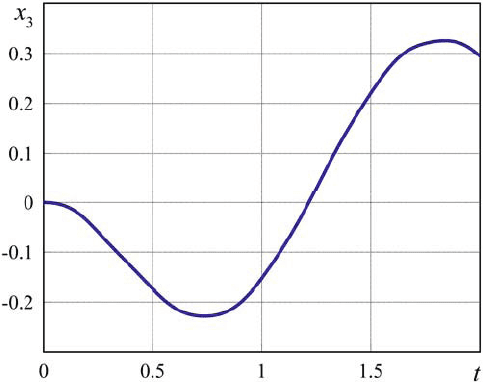
In the Fig. 3 the relative displacement of the central point

(, ,0,0) ()utL vt− of

the right free beam cross section versus time

t is shown.

Fig. 3. Relative displacement at the central point of the right free beam cross section vs. time.

Variational Approach to Static and Dynamic Elasticity Problems 153

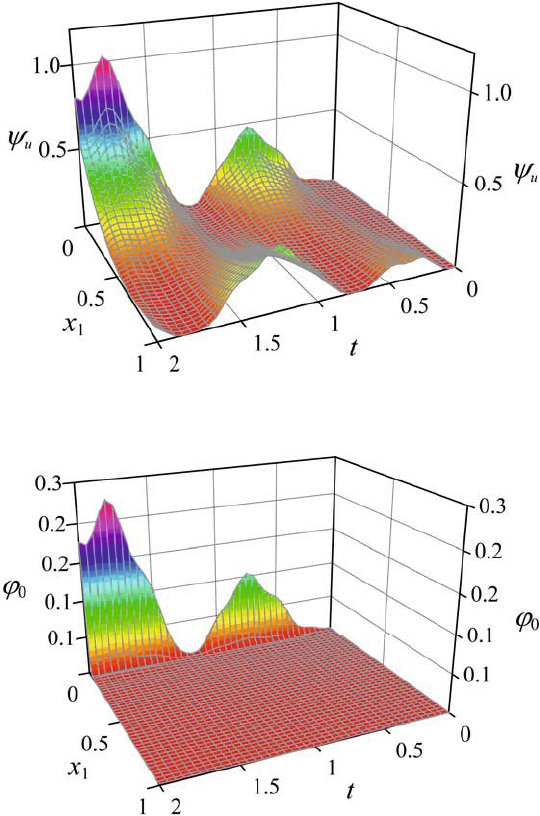
In Fig. 4 the function of energy linear density

11 23

(, )

t x dx dx

ψψ

−−

∫∫

is de-

pictured. The distribution of solution local error

11 023

(, )

t x dx dx

ϕϕ

−−

∫∫

along

axis

Ox is presented in Fig. 5. As it is seen from the figure the maximal errors is

concentrated in the area near the left cross section of the beam.

Fig. 4. Linear density of the total mechanical energy along beam axis.

Fig. 5. Distribution of solution local error along beam axis.

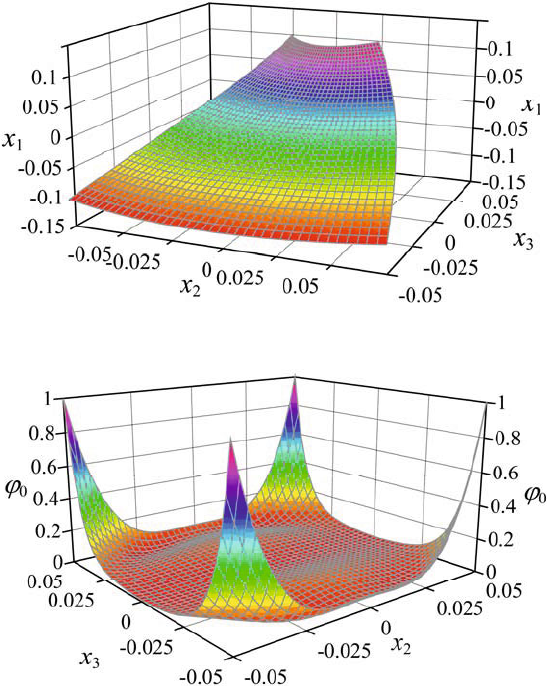
154 G.V. Kostin and V.V. Saurin

The 3D beam model takes into account space deflections in any beam cross

section at an arbitrary control instant. As an example, the deformed cross-section

shape of the beam at

0.8t = and

0.05x = is displayed in Fig. 6. The local error

distribution

in this cross section at the same time is shown in Fig. 7. The error

function on this rectangle reaches its maximal values at the beam edges.



Fig. 6. Deformed cross-section shape.



Fig. 7. Distribution of local error in a beam cross section at a fixed time instant.

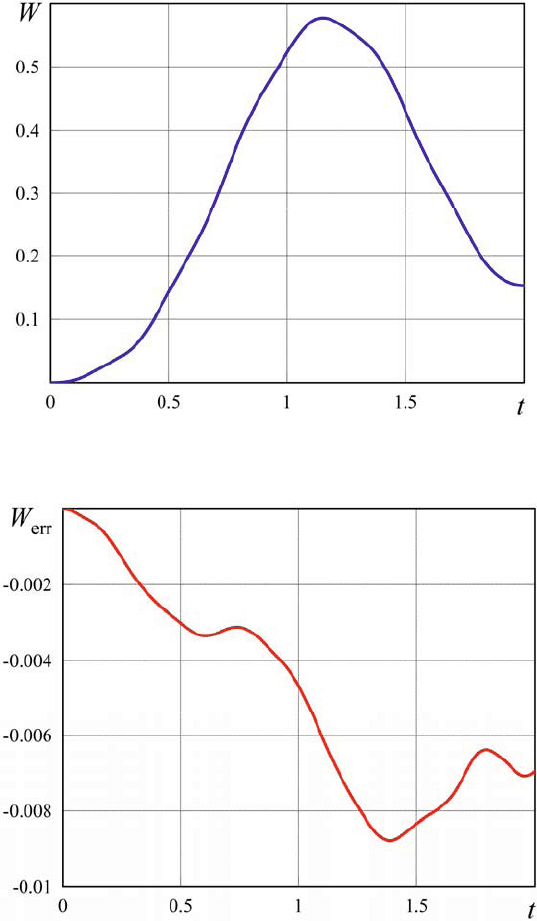
In this controlled process the total mechanical energy W starting with zero value

reaches its maximum during this motion as depictured in Fig. 8. The energy change

rate

err



caused by system discretization is reflected in Fig. 9. The numerical para-

sitic power defined in Eq. (62) result in noticeable energy underestimate. The linear

density distribution along beam axis

123

(, ) : :

t x dx dx

−−

∫∫



ξε for this

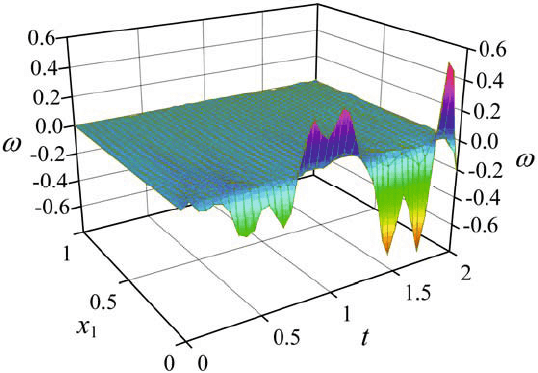
Variational Approach to Static and Dynamic Elasticity Problems 155

numerical disbalance is shown in Fig. 10. As it is seen from the figure the maximal

energy parasitic source is, analogously to the error distribution

, the area near the

left cross section of the beam.

Fig. 8. Mechanical energy versus time.

Fig. 9. Energy changes over numerical parasitic disbalance.

156 G.V. Kostin and V.V. Saurin

Fig. 10. Linear density distribution along beam axis for the numerical energy disbalance.

9 Conclusions

Based on the method of integrodifferential relations a family of variational princi-

ples which stationary conditions are equivalent to the constitutive relation was

deduced for the initial boundary value problems of linear elasticity. For these

principles the nonnegative functionals under minimization can serve as integral

criteria of the solution quality, whereas their integrands characterize the local error

distribution. In the case of dynamical boundary value problems under separated

boundary constraints on displacement and stress components one of the variational

formulations with the action-type functional is decomposed to the Hamilton

principle over displacements and its complementary principle on stress and

momentum fields.

The numerical algorithm used the time-space piecewise polynomial approxima-

tions enables one to construct effective estimates for various integral characteris-

tics (elastic energy, displacements, etc.). This algorithm can be directly applied to

nonhomogeneous anisotropic structures. The case of more complex boundary

conditions such as aero- and hydrodynamic forces, nonconservative loading, etc.

does not encounter principal difficulties. The polynomial spline technique (FEM)

incorporated in the algorithm allows one to consider bodies with irregular shapes.

The FEM realization will give one the possibility to work out various strategies of

p-h adaptive mesh refinement by using a local error estimate. The method can ap-

pear to be useful also in advanced beam, plate, and shell theories. The approach

worked out can be also applied to other inverse mechanical problems such as

shape optimization, identification, and so on as well as to optimal control prob-

lems with inequality constraints.

Variational Approach to Static and Dynamic Elasticity Problems 157

Acknowledgments

This work was supported by the Russian Foundation for Basic Research, project

nos. 08-01-00234, 09-01-00582, 10-01-00409, the Leading Scientific Schools Grant

NSh-3288.2010.1, NSh-64817.2010.1, and the German Research Foundation

(Deutsche Forschungsgemeinschaft DFG) under the grant number AS 132/2-1.

The authors also thank the Pericles S. Theocaris Fondation for financial support

during the Symposium on Recent Advances in Mechanics, Athens, Greece, Sep-

tember 16-19, 2009.

References

1. Akulenko, L.D., Kostin, G.V.: The perturbation method in problems of the dynamics

of inhomogeneous elastic rods. J. Appl. Math. and Mech. 56, 372–382 (1992)

2. Akulenko, L.D., Nesterov, S.V.: High-Precision Methods in Eigenvalue Problems and

their Applications. Charman & Hall/CRC, Boca Raton (2005)

3. Atluri, S.N., Zhu, T.: A new meshless local Petrov-Galerkin (MLPG) approach in

computational mechanics. Comput. Mech. 22, 117–127 (1998)

4. Belytschko, T., Lu, Y.Y., Gu, L.: Element-free Galerkin method. Int. J. Num. Methods

Eng. 37, 229–256 (1994)

5. Courant, R.: Variational methods for the solution of problem of equilibrium and vibra-

tion. Bulletin of American Math Society 49, 1–23 (1943)

6. Courant, R., Hilbert, D.: Methods of mathematical physics, vol. 1. Wiley, Chichester

(1937)

7. He, J.H.: Generalized variational principles for thermopiezoelectricity. Arch. Appl.

Mech. 72, 248–256 (2002)

8. Chernousko, F.L.: Control of elastic systems by bounded distributed forces. Appl.

Math. and Comp. 78, 103–110 (1996)

9. Chernousko, F.L., Ananievski, I.M., Reshmin, S.A.: Control of Nonlinear Dynamical

Systems: Methods and Applications. Springer, Heidelberg (1996)

10. Leineweber, D., Bauer, E.I., Bock, H., et al.: An efficient multiple shooting based re-

duced SQP strategy for large dynamic process optimization. Part 11: Theoretical as-

pects. Comp. and Chem. Eng. 27, 157–166 (2003)

11. Kostin, G.V., Saurin, V.V.: Integro-differencial approach to solving problems of linear

elasticity theory. Doklady Physics 50, 535–538 (2005)

12. Kostin, G.V., Saurin, V.V.: Modeling of controlled motions of an elastic rod by the

method of integro-differential relations. J. Comp. and Sys. Sci. Int. 45, 56–63 (2006)

13. Kostin, G.V., Saurin, V.V.: The optimization of the motion of an elastic rod by the

method of integro-differential relations. J. Comp. and Sys. Sci. Int. 45, 217–225 (2006)

14. Kostin, G.V., Saurin, V.V.: Modeling and optimization of elastic system motions by

the method of integro-differential relations. Doklady Math. 73, 469–472 (2006)

15. Kostin, G.V., Saurin, V.V.: The method of integrodifferential relations for linear elas-

ticity problems. Arch. Appl. Mech. 76, 391–402 (2006)

16. Kostin, G.V., Saurin, V.V.: Variational statement of optimization problems for elastic

body motions. Doklady Mathematics 76(1), 629–633 (2007)

17. Kostin, G.V., Saurin, V.V.: An asymptotic approach to the problem of the free oscilla-

tions of a beam. J. Appl. Math. and Mech. 71, 611–621 (2007)

158 G.V. Kostin and V.V. Saurin

18. Kostin, G.V., Saurin, V.V.: A variational formulation in fracture mechanics. Int. J.

Fructure 150, 195–211 (2008)

19. Kostin, G.V., Saurin, V.V.: Motion analysis and optimization for beam structures. In:

Awrejcewicz, J. (ed.) Modeling, Simulation and Control of Nonlinear Engineering

Dynamical Systems: State-of-the-Art, Perspectives and Applications. Springer, Nether-

lands (2008)

20. Kwon, K.C., Park, S.H., Jiang, B.N., et al.: The least-squares meshfree method for

solving linear elastic problems. Comp. Mech. 30, 196–211 (2003)

21. Saurin, V.V.: Variational approaches in the linear theory of elasticity. Doklady

Phys. 52(8), 426–430 (2007)

22. Washizu, K.: Variational methods in elasticity and plasticity. Pergamon Press, Oxford

(1982)