Костюков В.Н., Науменко А.П., Бойченко С.Н., Тарасов Е.В. Основы виброакустической диагностики машинного оборудования
Подождите немного. Документ загружается.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
51
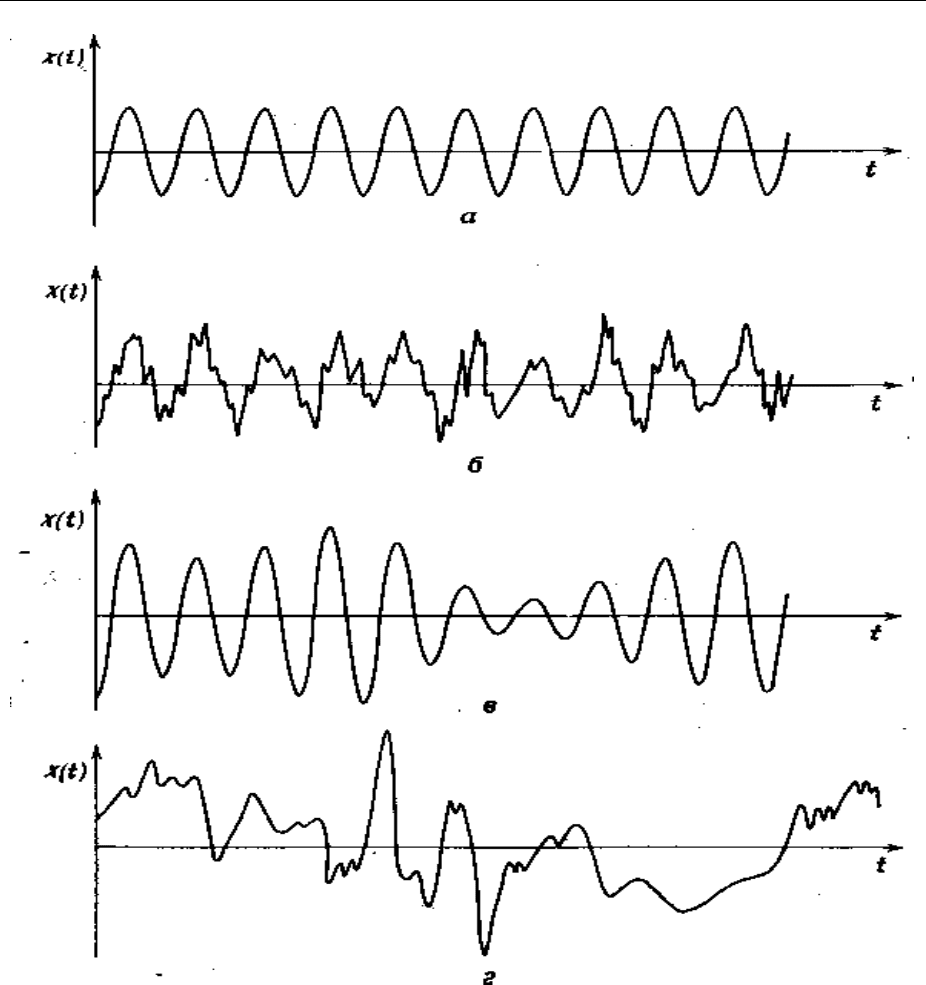
Рисунок 3-25 - Четыре примера реализаций случайных процессов:
а — гармонический процесс; б — гармонический процесс плюс случайный
шум; в — узкополосный случайный шум; г — широкополосный случайный
шум
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
52
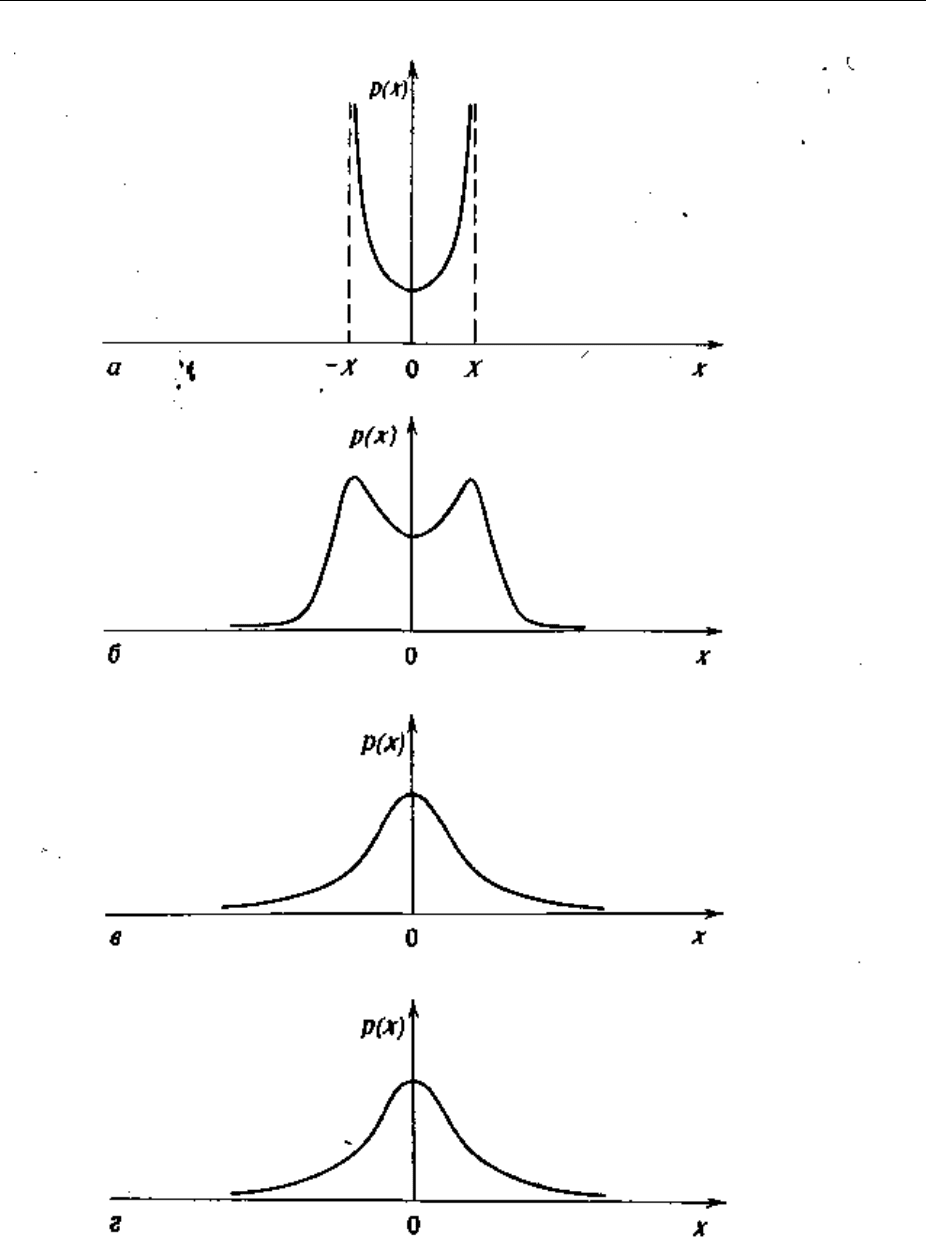
Рисунок 3-26 - Плотности вероятности: а — гармонический процесс;
б — гармонический процесс плюс случайный шум; в — узкополосный слу-
чайный шум; г — широкополосный случайный шум

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
53
В случае стационарного процесса ширину интервала
W
следует устре-
мить к нулю; но на практике она всегда конечна. Функция
)
(
x
p
удовлетворя-
ет при всех x условию
0
)
(
³
x
p
, а площадь под кривой
)
(
x
p
равна единице.
Функция распределения
)
(
x
P
показывает вероятность того, что в лю-
бой момент времени
t
значение
)
(
t
x
удовлетворяет условию
x
t
x
£
)
(
. Функ-
ция распределения связана с плотностью вероятности соотношением
()()
x
Pxpudu
=
-¥
ò
,
где
u
– переменная интегрирования. При этом
0
)
(
=
-¥
P
и
1
)
(
=
-¥
P
.
Плотность вероятности Гауссова или нормального стационарного слу-
чайного процесса
)
(
t
x
описывает значения, которые в любой времени
t
под-
чиняются закону
1
22
()exp()/2,,
2
pxxx
xx
x
ms
sp
éù
=---¥¥
êú
ëû
<<
где
m
- истинное среднее значение процесса,
2
x
s
- истинная дисперсия.
В качестве характеристик закона распределения в статистике исполь-
зуют его моменты до четвертого включительно. Первый момент - математи-
ческое ожидание
[]()
MXxPxx
kk
k
==
å
, (3.39)
соответствующее среднему значению случайной величины.
В качестве меры рассеивания используют второй центральный момент
или дисперсию:
2
2
[][()].
x
DXMXm
m
==- (3.40)
Меру рассеяния, имеющую размерность математического ожидания
или случайной величины, называют средним квадратическим или средне-
квадратичным или стандартным отклонением
[
]
DX
s
= (3.41)
Рисунок 3-26 представляет вычисленные теоретические плотности ве-
роятности реализаций для различных видов процессов.
Среднее значение
x
m
и дисперсия
2
x
s
стационарной реализации слу-
чайного процесса характеризуют соответственно центр рассеяния и величину
рассеяния данных. Средний квадрат
2
x
Y , равный сумме дисперсии и квадра-
та среднего значения, является мерой того и другого одновременно. Среднее
значение оценивается простым усреднением всех значений реализации. Ана-
логичным усреднением квадратов значений реализации оценивается средний
квадрат. Если перед возведением в квадрат из значений реализаций вычитать
среднее значение, то такое усреднение даст оценку дисперсии.
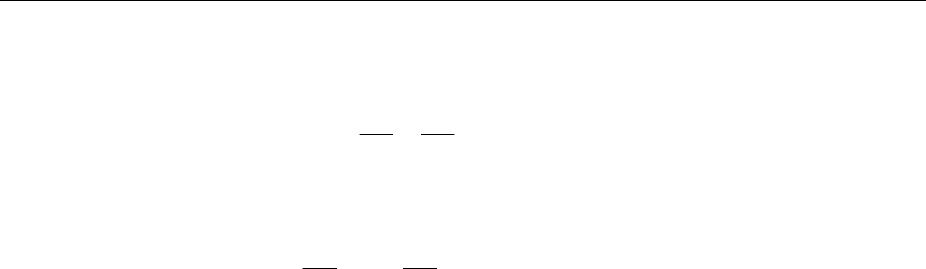
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
54
Характеристикой асимметрии эмпирического распределения является
показатель асимметрии
3
3
33
1
[()]
sx
AMXm
m
ss
==-
.
В качестве характеристики большей или меньшей "вершинности", по
сравнению с нормальной кривой распределения, используют эксцесс
4
4
44
1
3[()]3
x
k
MXm
m
e
ss
=-=--
. (3.42)
Для нормального распределения эксцесс равен нулю. Кривые, более
островершинные, по сравнению с нормальной, обладают положительным
эксцессом; кривые более плосковершинные - отрицательным эксцессом.
Часто используют такую характеристику положения случайной вели-
чины на числовой оси как медиана. Медианой случайной величины
X
такое
ее значение
e
m
, для которого
()()
ee
PXPX
mm
=
<>
, (3.43)
т.е. одинаково вероятно, окажется ли случайная величина меньше или боль-
ше
e
m
. Геометрическая медиана - это абсцисса точки, в которой площадь
кривой, ограниченная кривой распределения, делится пополам.
Форма одномерного закона распределения случайного процесса
)
(
t
x
,
заданная в виде
n
-мерного вектора отсчетов его амплитуды )(
k
xP - носитель
информации о параметрах состояния объекта исследования. Несмотря на то,
что только совокупность всех конечномерных распределений дает исчерпы-
вающую информацию о случайном процессе, в ряде практических случаев
даже одномерный
)
(
x
P
и двумерный
)
,
(
y
x
P
законы распределения ампли-
туд колебательных процессов являются достаточно представительными ха-
рактеристиками, которые могут быть использованы в качестве диагностиче-
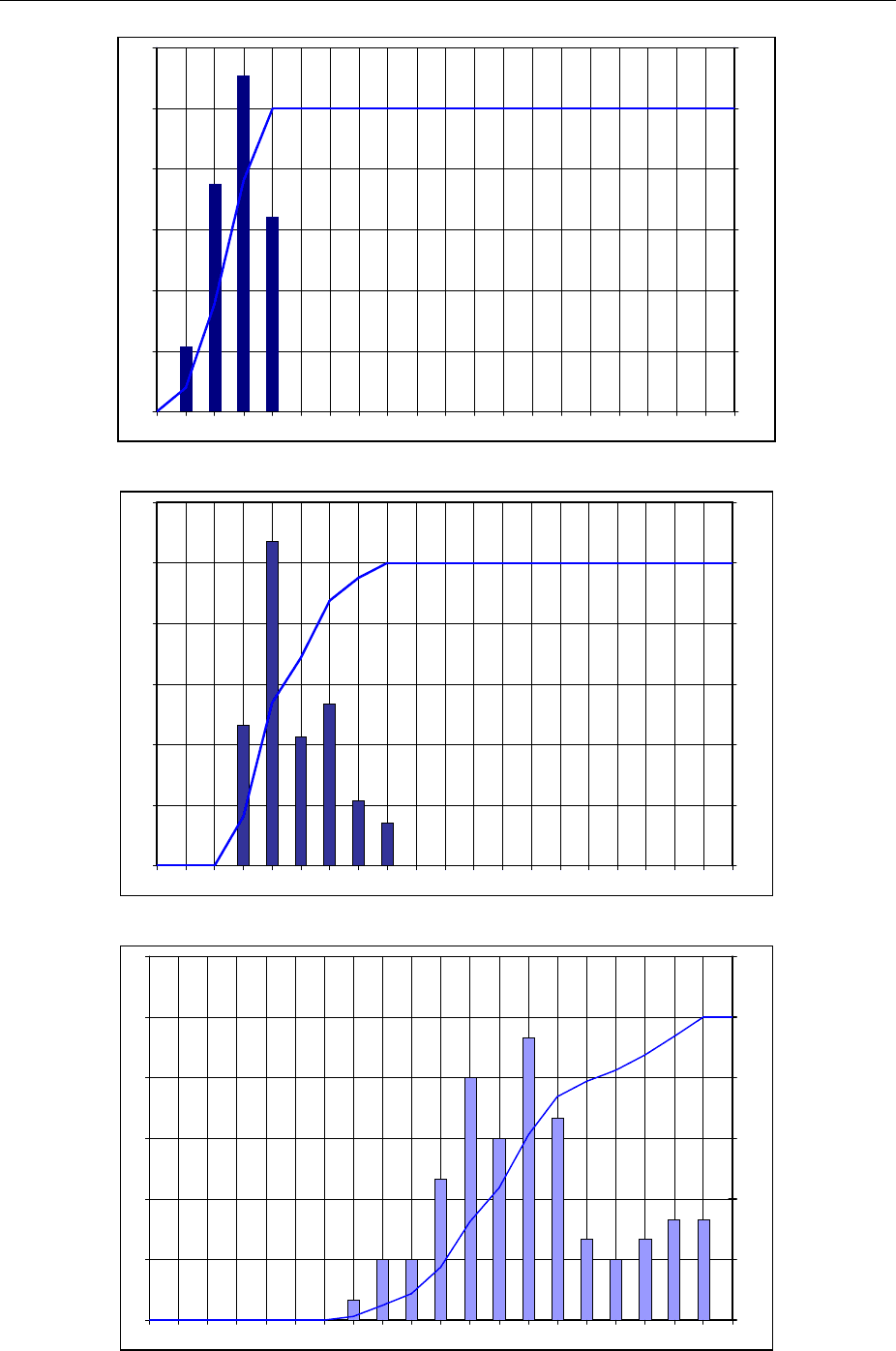
ских признаков состояния механизма. Гистограммы частот попадания значе-
ний тренда виброускорения с датчика нагнетательного клапана в состоянии
«Допустимо», «Требует принятия мер» «Недопустимо» в интервалы значе-
ний характеризуют состояния клапана (Рисунок 3-27, Рисунок 3-28, Рисунок
3-29).
3.18. Ковариационная функция
Ковариационная функция )(
t
xx
R стационарного процесса задает меру
зависимости его значений, сдвинутых относительно друг друга на опреде-
ленный интервал времени. Чтобы оценить ковариационную функцию, следу-
ет сдвинуть реализацию на время
t
, перемножить исходную и сдвинутую
реализации и усреднить полученные произведения по всей реализации или
по некоторому ее отрезку. Эта процедура выполняется для всех требуемых
значений сдвига времени.
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
55
0
0.07
0.14
0.21
0.28
0.35
0.42
30 40 50 60 70 80 90 100 110 120 130
Ara, м/с2
p(Ara)
0%
20%
40%
60%
80%
100%
120%
F(p)
Рисунок 3-27 – Состояние «Допустимо»
0
0.07
0.14
0.21
0.28
0.35
0.42
30 40 50 60 70 80 90 100 110 120 130Ara, м/с2
p(Ara)
0%
20%
40%
60%
80%
100%
120%
F(p)
Рисунок 3-28 - Состояние «Требует принятия мер»
0
3
6
9
12
15
18
30 40 50 60 70 80 90 100 110 120 Еще
Ara, м/с2
p(Ara)
0%
20%
40%
60%
80%
100%
120%
F(p)
Рисунок 3-29 – Состояние «Недопустимо»
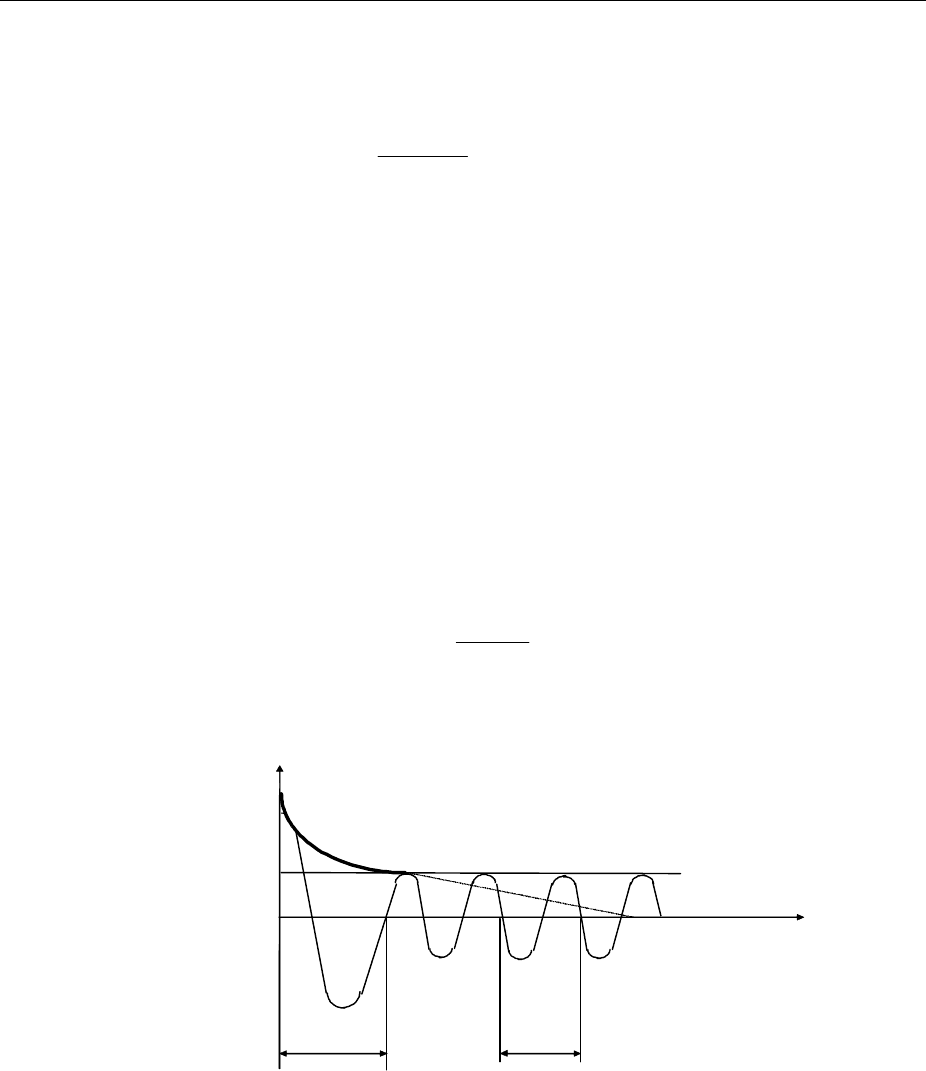
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
56
Функция автокорреляции стационарного случайного процесса
)
(
t
s
на
конечном интервале наблюдения
)
,
0
(
T
имеет оценку:
max
max
0
1
()()()
T
SS
Kststdt
T
t
tt
t
-
=+
-
ò
, (3.44)
где
max
t
- максимальное значение сдвига по времени.
Несмотря на то, что функция автокорреляции несет ту же информацию,
что и спектральная плотность
)
(
w
G
, так как эти функции связаны между со-
бой парой преобразования Фурье, на практике встречаются случаи, когда по-
ведение функции корреляции более наглядно отражает изменение состояния
объекта диагностирования, например, при изменении соотношения энергии
периодической и шумовой компонент
Ш
П
EE /
(Рисунок 3-31). Рисунок 3-31
представляет вычисленные ковариационные функции реализаций для раз-
личных видов процессов.
При появлении дефекта, связанного с возбуждением периодического
процесса с периодом
T
, зависимость нормированной функции корреляции от
t
)0(
)(
)(
ss
ss
ss
K
K
t
tr
= , (3.45)
становится периодической при
0
t
t
>
, где
0
t
- интервал корреляции шумовой
компоненты с амплитудой, равной отношению
Ш
П
EE / .
t
r
ss
1
E
П
/E
Ш
t
T
Рисунок 3-30 – Коэффициент автокорреляции
Этот уровень может быть использован в качестве диагностического
признака дефекта, характеризующего появление или увеличение уровня пе-
риодической составляющей с периодом
T
.
На рисунке 3.31 сплошной линией изображена огибающая коэффици-
ента корреляции при наличии периодической составляющей, штриховой ли-
нией - при ее отсутствии.
При явлениях износа, связанных с увеличением шероховатости контак-
тирующих поверхностей, наблюдается обратное явление, т.е. возрастает роль
шумовой компоненты. Это обстоятельство также отражается на внешнем ви-
де )(
t
r
ss
: уменьшается отношение
Ш
П
EE /
и увеличивается коэффициент
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
57
затухания функции )(
t
r
ss
, который может служить диагностическим при-
знаком.
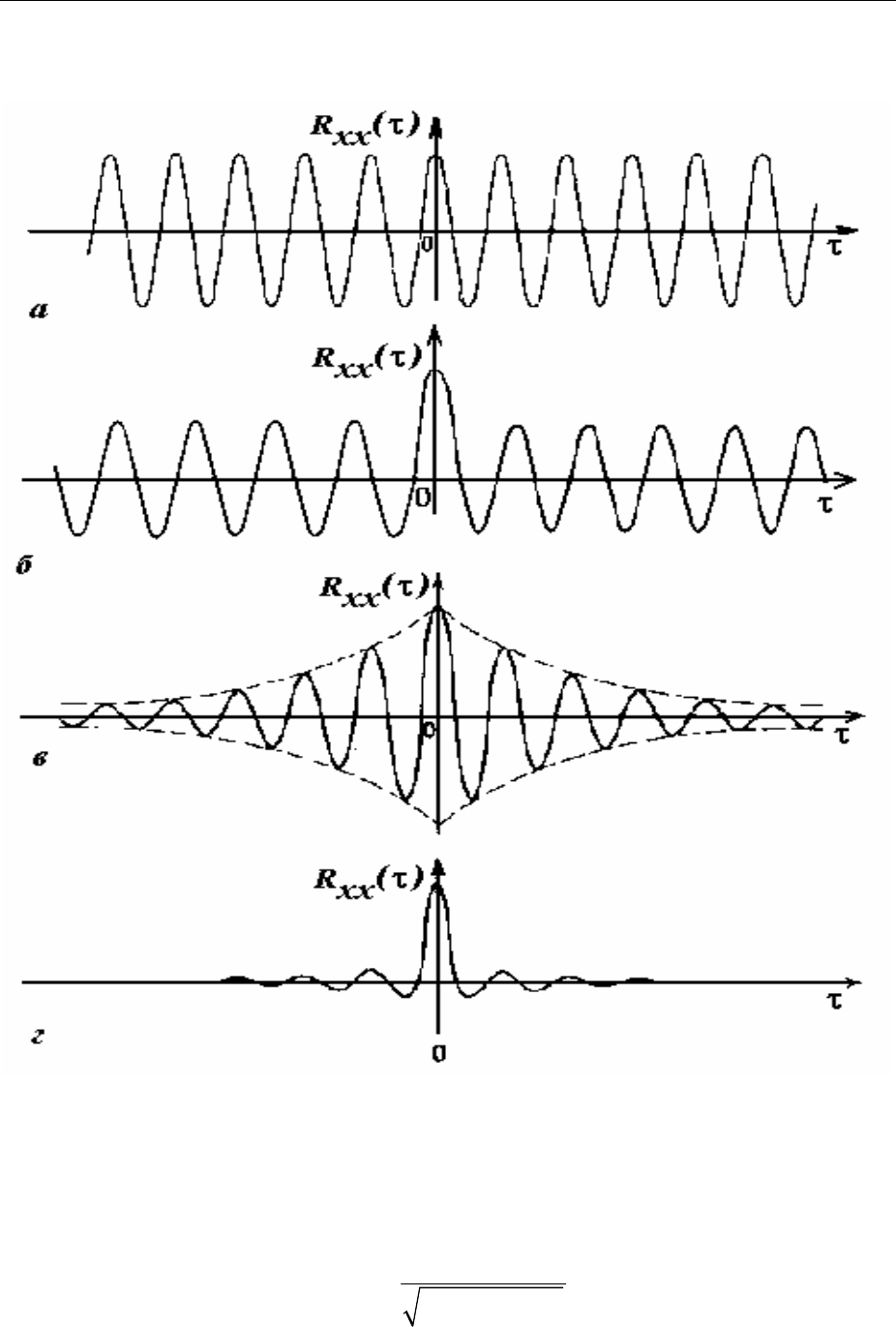
Рисунок 3-31 - Ковариационные функции: а — гармонический процесс;
б — гармонический процесс плюс случайный шум; в — узкополосный слу-
чайный шум; г — широкополосный случайный шум
В качестве диагностического признака может быть использовано мак-
симальное значение коэффициента взаимной корреляции
()
()
(0)(0)
xy
xy
xxyy
K
KK
t
rt
= , (3.46)
процессов
)
(
t
x
и
)
(
t
y
, измеренных в различных точках агрегата. Наиболее
эффективно использовать его, если
)
(
t
x
- входной, а
)
(
t
y
- выходной процесс
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
58
объекта. Появление дополнительного некогерентного возбуждения внутри
узла непременно проявит себя уменьшением значения
max()
xy
rt
.
3.19. Спектральная плотность мощности
К числу важнейших характеристик относится спектральная плот-
ность, которая пропорциональна средней мощности колебательного процес-
са, отнесенной к единице частотного диапазона при заданной частоте. Спек-
тральная плотность случайного процесса, как неслучайная его оценка, явля-
ется непрерывной функцией частоты. Рисунок 3-32 представляет спектраль-
ные плотности реализаций гармонического процесса, гармонического про-
цесса в случайном шуме, узкополосного шума и широкополосного шума.
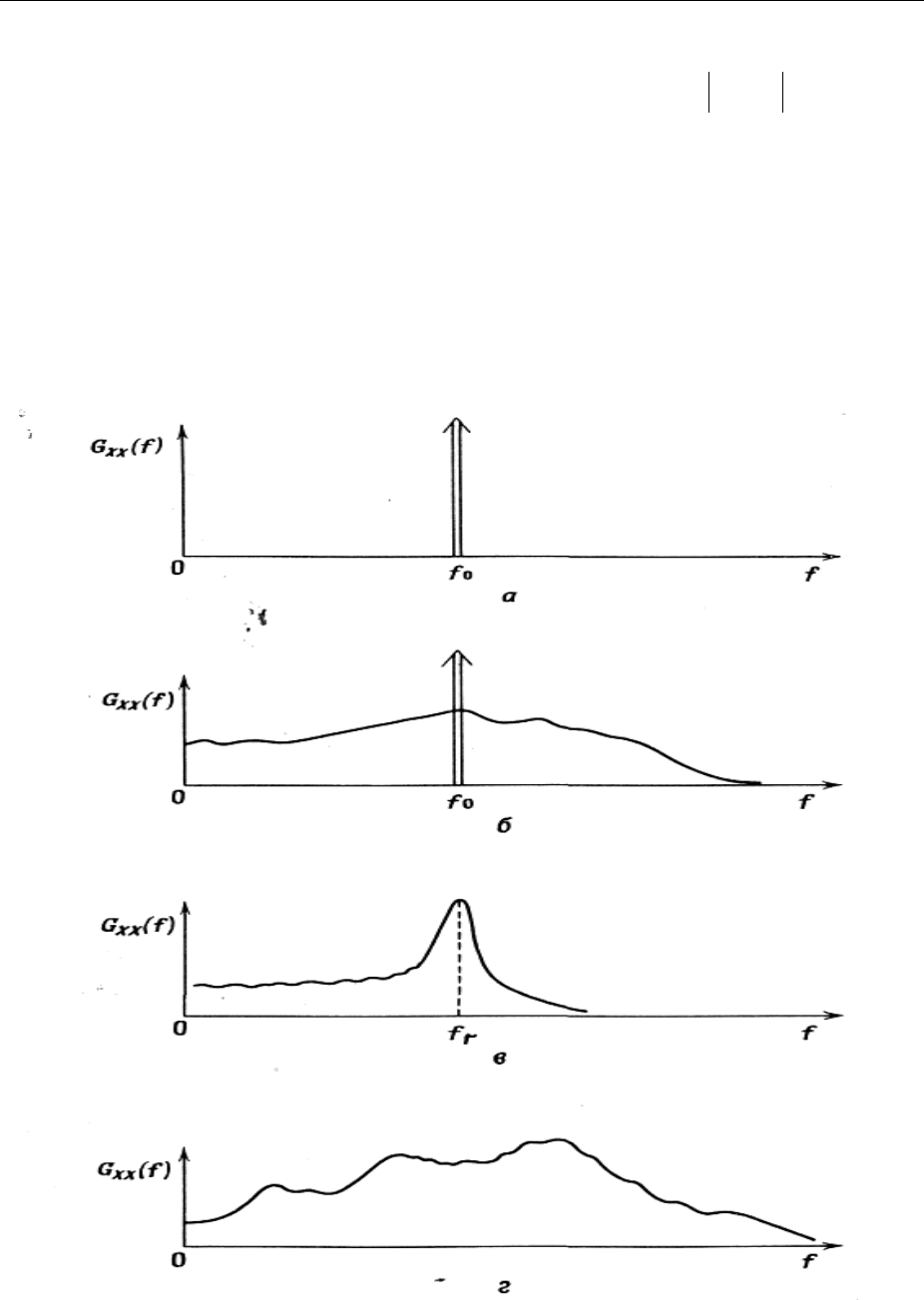
Рисунок 3-32 - Спектральные плотности:
а — гармонический процесс; б — гармонический процесс плюс случайный
шум; в — узкополосный случайный шум; г — широкополосный случайный
шум

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
59
Спектральная плотность (иначе, спектр мощности)
()
xx
Gf
стационар-
ной реализации интерпретируется как распределение среднего квадрата по
частоте. Для оценивания спектра вычисляется средний квадрат в узкой поло-
се частот при разных центральных частотах, а затем полученное значение де-
лится на ширину этой полосы. Общая площадь, лежащая под графиком спек-
тральной плотности во всей полосе частот, равна суммарному среднему
квадрату реализации. Часть этой площади, заключенная между частотами
1
f
и
2
f
равна среднему квадрату, сосредоточенному в этой полосе частот.
Узкополосным называется случайный процесс, спектральная плот-
ность которого существенно отлична от нуля лишь в пределах узкой полосы
частот, сосредоточенной вблизи некоторой центральной частоты.
Если мгновенные значения процесса имеют гауссовское распределение
вероятностей, то его экстремальные значения приближенно подчиняются
распределению Релея.
Если реализация стационарного случайного процесса
)
(
t
s
задана на ог-
раниченном интервале времени
)
,
0
(
T
и равна нулю вне его, то за оценку
спектральной плотности мощности принимают величину
2
()
()
lim
T
S
G
T
w
w
®¥
= , (3.47)
которая дает усредненную картину распределения мощности по частоте.
В качестве диагностического признака вместо спектрального разложе-
ния процесса иногда используют интегральную характеристику - дисперсию
шума:
2
1
2
()
2
1
Gd
w
sww
p
w
=
ò
, (3.48)
в полосе частот ),(
21
w
w
, где изменения виброакустического сигнала прояв-
ляются наиболее заметно.
При диагностике объекта на каждом режиме работы полезно иметь
таблицу основных частот возбуждения колебаний и их гармоник с тем, чтобы
вести направленный поиск диагностических признаков. В ряде случаев в ка-
честве диагностического признака может служить спектральная амплитуда
на частоте возбуждения диагностируемого узла, если ее поведение однознач-
но связано с изменением соответствующего параметра состояния объекта.
При наличии в спектре четко выраженного гармонического ряда или
нескольких рядов частот, кратных основным частотам возбуждения объекта,
удобно формировать диагностический признак из составляющих гармониче-
ского ряда, амплитуды гармоник которого несут информацию об изменении
состояния узла объекта диагностирования. При этом наиболее простым и
информативным признаком служит длина
n
-мерного вектора, компонентами

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _
60
которого являются амплитуды A
i
гармонического ряда. В ряде случаев доста-
точно ограничиться числом ряда
10
...
5
=
n
.
3.20. Взаимный спектр
Преобразование Фурье от функции взаимной корреляции - взаимный
спектр
1
()()
2
jt
xyxy
GjKed
w
wtt
p
¥
-
-¥
=
ò
, (3.49)
может быть использован для формирования диагностических признаков. Мо-
дуль взаимного спектра
)(
w
xy
G
характеризует распределение по частоте
энергии взаимодействия колебательных процессов
)
(
t
x
и
)
(
t
y
. Этот факт
может быть использован для формирования характерных диагностических
признаков по аналогии со спектром мощности. Одно из распространенных
применений функции взаимной спектральной плотности - определение пере-
даточной функции линейной модели объекта при случайных входных воз-
мущениях:
()
()
()
xy
xx
Gj
Hj
G
w
w
w
= . (3.50)
Поскольку в режиме нормального функционирования объекта реально
действующее на вход диагностируемого узла возбуждение может иметь про-
извольный спектр, передаточная функция не может быть определена на час-
тотах, где 0)(
=
w
xx
G . Если при появлении дефекта изменяется передаточная
функция узла (смещаются собственные частоты за счет изменения, напр., же-
сткости какого-либо сопряжения, изменяется амплитуда при изменении
демпфирования или фазовый сдвиг между входом и выходом), то любой из
этих параметров может быть использован в качестве диагностического при-
знака.
3.21. Кепстр
При применении методов, относящихся к определению кепстров, учи-
тываются функции, которые можно рассматривать как «спектры
логарифмических спектров». По существу понятие кепстров было введено в
1963 г. в связи с определением кепстра мощности как «спектра мощности
логарифмического спектра мощности». Кепстр мощности был предложен в
качестве более эффективной альтернативы ковариационной
(автокорреляционной) функции при обнаружении эха в сейсмических
сигналах. Так как соответствующая функция по определению отображает
спектр спектра, то воспользовались терминологической аналогией и согласно
термину «спектр» дали этой функции название «кепстр», где первые четыре
буквы просто расположены в обратном порядке. Аналогичным образом
возникли термины «квефренция» (quefrency), «рагмоника» (rahmonica),
«лифтр» (lifter), “гамнитуда” (gamnituda), и «сафе» (saphe), основанные на
аналогии с английскими терминами для частоты (frequency), гармоники
