Костюков В.Н., Науменко А.П., Бойченко С.Н., Тарасов Е.В. Основы виброакустической диагностики машинного оборудования

Подождите немного. Документ загружается.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

()()()

Atxtxt

;

()[()/()]

tarctgxtxt

;

()()()()

()()

xtxtxtxt

xtxt

%%%

(3.34)

Исходный колебатель-

ный процесс

)

(

нигде не

пересекает свою огибающую

)

(

, а в точках соприкосно-

вения имеет общие касатель-

ные (Рисунок 3-20

). При

редставлении случайного

процесса

)

(

в виде (3.30

) он

может рас

сматриваться как

гармоническое колеба

ние,

модулированное по амплиту-

де и частоте случай

ными

функциями

)

(

)

(

. Ана-

лизируя особенности измене-

ния соответствующих мгно-

венных характеристик, мож-

но уточнить конкрет

ный вид

модуляции исходного про-

цесса. В ряде случаев, когда

разли

чить случаи биений и

амплитуд

ной модуляции по

виду процесса или поведе-

нию огибающей не

возможно

в связи с их внешним сходст-

вом, проводится анализ изме-

нения мгновенной фазы (час-

тоты) или спектра процесса.

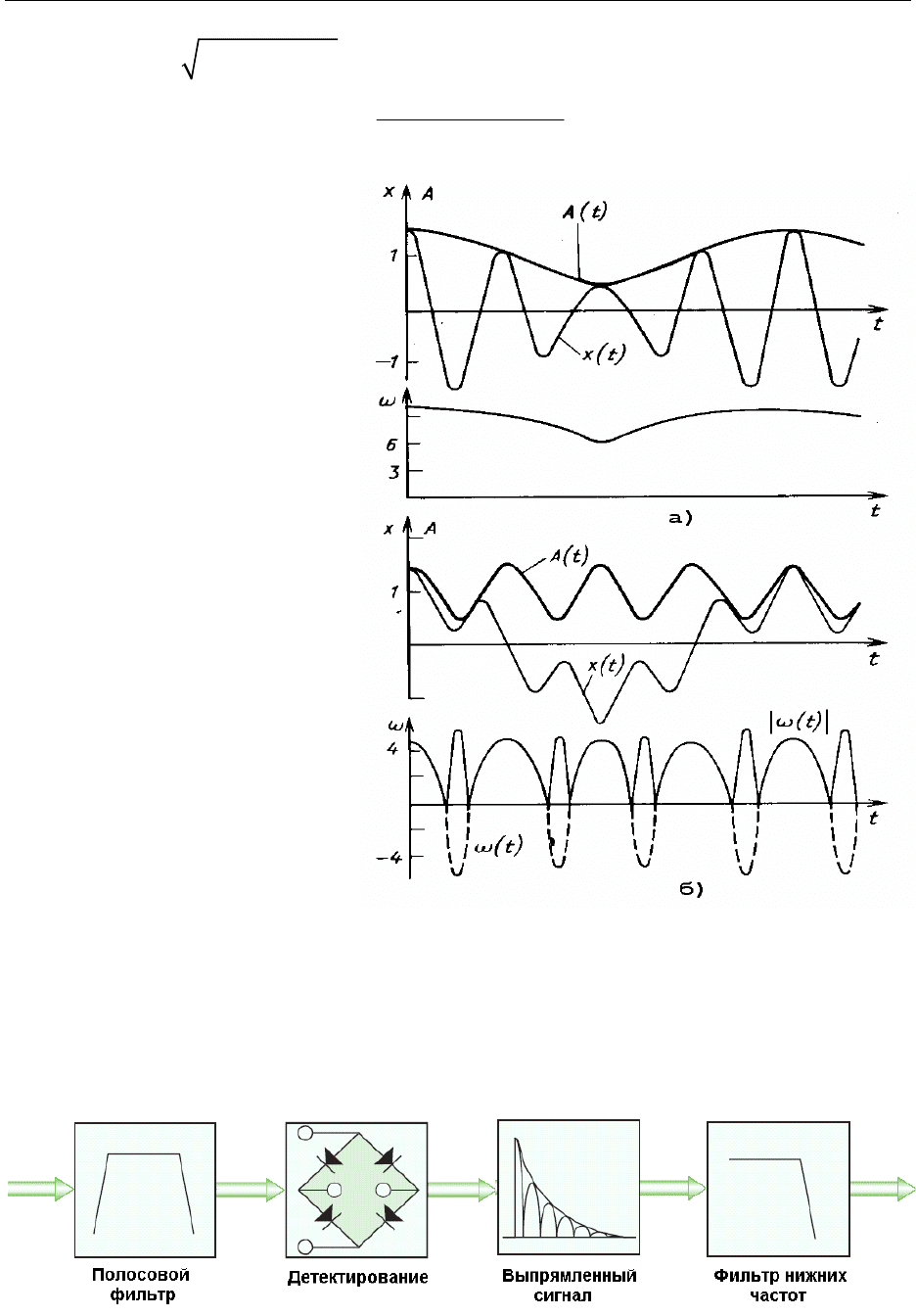
Рисунок 3-20 - Колебательный процесс и его

мгновенные амплитуда и частота:

а – узкополосный; б – широкополосный

На практике, огибающая АМ сигнала выделяется в требуемой полосе

частот по алгоритму, приведенному на рисунке 3-21.

Рисунок 3-21 – Алгоритм выделения огибающей

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

3.8. Непериодические колебания

В общем случае спектральный анализ непериодических колебаний мо-

жет давать бесконечно большую сумму гармонических составляющих, рас-

стояние между спектральными линиями которых становится бесконечно ма-

лым, что превращает спектр из дискретного в непрерывный (сплошной).

К числу непериодических установившихся колебаний относятся почти

периодические колебания, например, в виде суммы нескольких гармоник,

частоты которых не находятся между собой в рациональном отношении.

Почти периодические колебания обычно имеют дискретный спектр с несоиз-

меримыми частотами гармоник.

Следует отметить, что при суммировании хотя бы пяти-шести гармо-

нических колебаний с взаимно независимыми частотами получается процесс,

практически неотличимый от случайного, близкого к нормальному [92, 17].

Следовательно, при достаточно большом числе гармоник почти периодиче-

ский процесс приобретает все свойства случайного.

Еще одним примером непериодических установившихся колебаний яв-

ляются почти гармонические, модулированные по амплитуде, частоте и

(или) фазе непериодическими функциями времени. Такие колебания могут

иметь не только непрерывный, но и дискретный спектр. К непериодическим

колебаниям относятся также: сравнительно короткие отрезки периодических

колебаний, в частности, участок моногармонического процесса, и переход-

ные (неустановившиеся) колебания, например, затухающие или нарастающие

во времени процессы; импульсы или последовательность нескольких им-

пульсов самой разнообразной формы: типа скачка, прямоугольной, колоко-

лообразной и т. п. форм. В последнем случае непрерывный спектр одиночно-

го импульса и огибающая дискретного спектра периодической последова-

тельности, полученной путем повторения этого импульса, совпадают по

форме. С увеличением числа импульсов в последовательности непрерывный

спектр все более расщепляется и в пределе принимает дискретную структуру.

Переходным называется детерминированный или случайный процесс,

имеющий конечную длительность.

3.9. Случайные колебания

Большинство колебательных процессов, с которыми приходится встре-

чаться на практике, носят в той или иной степени случайный характер, при

этом текущие значения процесса могут быть определены лишь с некоторой

вероятностью. Случайный колебательный процесс может быть представлен

совокупностью статистических характеристик, постоянных или переменных

во времени.

3.10. Классификация случайных процессов

Как указывалось ранее, процесс, описывающий случайное физическое

явление, нельзя задать явной математической зависимостью, поскольку каж-

дое наблюдение этого явления дает невоспроизводимый результат. Другими

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

словами, любое наблюдение дает только один вариант из множества возмож-

ных. Рассмотрим, например, напряжение на выходе генератора теплового

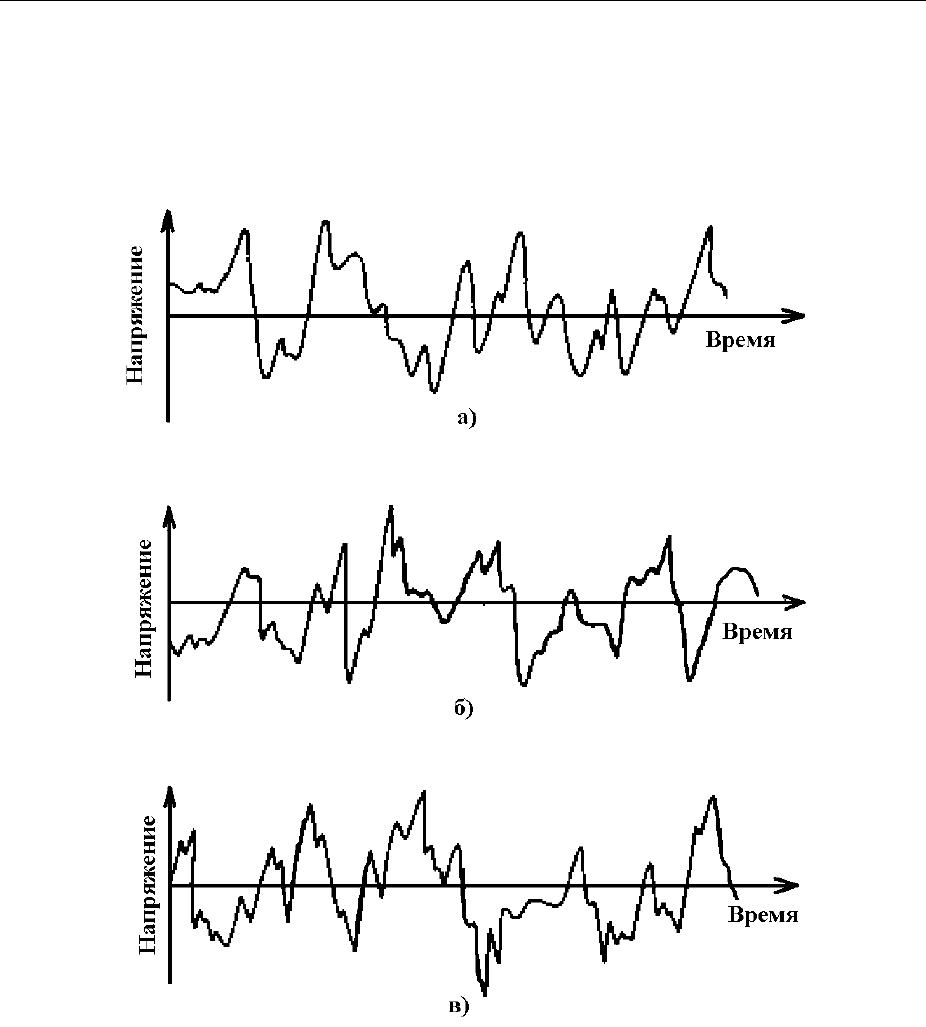
шума как функцию времени. Фиксируя временные реализации сигнала в раз-

личные моменты времени, получим различные реализации зависимости на-

пряжения от времени (Рисунок 3-22 а), б), в)).

Рисунок 3-22 - Выборочные функции на выходе генератора теплового шума

Конкретная реализация процесса, описывающего случайное явление,

называется выборочной функцией (или реализацией, если речь идет о наблю-

дении конечной длительности). Совокупность всех возможных выборочных

функций, которые может дать случайное явление, называется случайным или

стохастическим процессом. Таким образом, под реализацией случайного яв-

ления понимается один из возможных исходов случайного процесса.

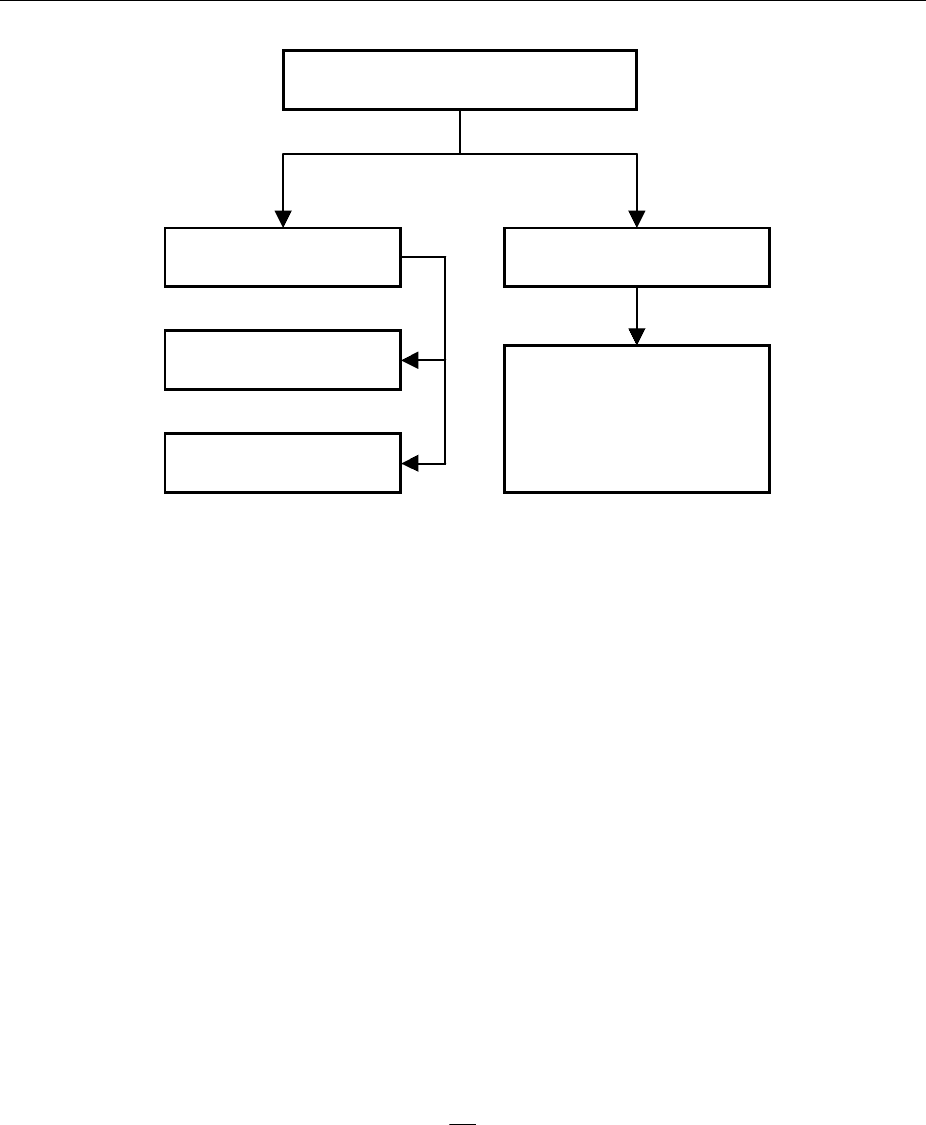
Случайные процессы делятся на стационарные и нестационарные. В

свою очередь стационарные случайные процессы – на эргодические и неэр-

годические. Дальнейшая классификация нестационарных случайных процес-

сов проводится по особенностям их не стационарностей (Рисунок 3-23).

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Случайные процессы

Стационарные Нестационарные

Эргодические

Неэргодические

Классификация

по типам

нестационарности

Рисунок 3-23 – Классификация случайных процессов

3.11. Стационарные случайные процессы

Если физическое явление описывается случайным процессом, то свой-

ство этого явления в принципе можно оценить в любой момент времени пу-

тем усреднения по совокупности выборочных функций, образующих случай-

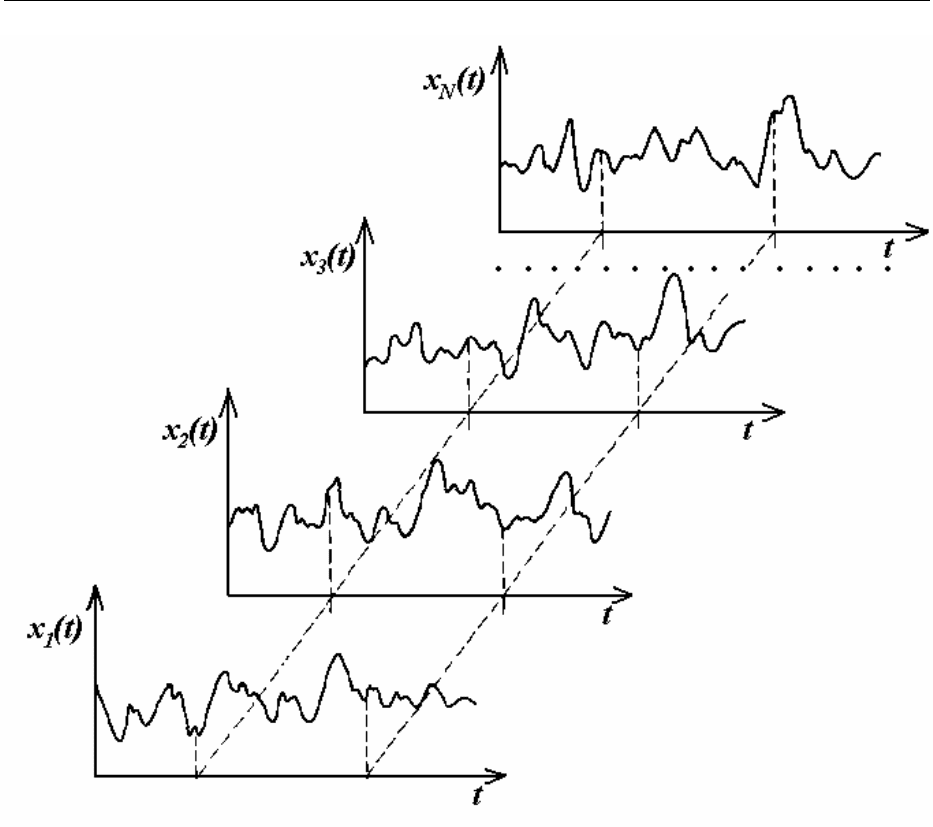
ный процесс. Рассмотрим, например, совокупность выборочных функций

(называемую также ансамблем) (Рисунок 3-24), определяющую случайный

процесс.

Среднее значение (первый момент) этого случайного процесса в мо-

мент времени

можно вычислить, взяв мгновенные значения всех выбороч-

ных функций ансамбля в момент времени

, сложив эти значения и разделив

на число выборочных функций.

Следовательно, среднее значение

()

случайного процесса

{

}

)(tx , где

символ

{

}

обозначает ансамбль выборочных функций, определяется форму-

лой

()lim()

txt

®¥

, (3.35)

в которой суммирование производится в предположении равновероятности

всех выборочных функций.

В общем случае, когда

()

, определенно уравнением (3.34), зависит

от момента времени

, случайный процесс

{

}

)(tx называется нестационар-

ным. В том частном случае, когда

()

не зависит от момента времени

случайный процесс называется слабо стационарным или стационарным в

широком смысле. Среднее значение слабо стационарного процесса постоян-

но, а ковариационная функция зависит только от сдвига времени

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Свойство инвариантности статистических характеристик относительно

произвольного момента времени используется для классификации случайных

колебательных процессов. Все статистические характеристики случайного

стационарного колебательного процесса инвариантны по отношению к мо-

менту времени. Таким образом, случайный стационарный процесс есть ан-

самбль реализаций, статистические свойства которого инвариантны по от-

ношению к переносу начала отсчета времени. Случайные стационарные ко-

лебания служат удобной моделью реальных процессов, свойства которых

достаточно медленно изменяются во времени.

Случайный процесс называется стационарным в широком смысле, если

его среднее значение постоянно (не зависит от времени), а автокорреляция

зависит только от временного сдвига. Обычно при определении среднего

значения, корреляции и спектральной плотности мощности случайного про-

цесса используют статистическое усреднение по ансамблю. Однако на прак-

тике обычно не удается получить ансамбль реализаций требуемого процесса,

по которому можно было бы вычислить эти статистические характеристики.

Желательно оценивать все статистические свойства по одной выборочной

реализации

)

(

, заменяя усреднение по ансамблю усреднением по времени.

Свойство, позволяющее такую замену осуществить, называют эргодично-

стью.

В общем случае для определения полного набора функций распределе-

ния, задающих структуру случайного процесса

{

}

)(tx , нужно вычислить бес-

конечное число моментов и смешанных моментов высших порядков. В том

случае, когда все моменты и смешанные моменты инвариантны во времени,

случайный процесс

{

}

)(tx называется строго стационарным или стационар-

ным в узком смысле. Во многих приложениях проверка слабой стационарно-

сти позволяет обосновать строгую стационарность.

3.12. Эргодические случайные процессы

Определить характеристики случайного процесса можно путем усред-

нения по ансамблю в определенные моменты времени. Возьмем, например,

-ю выборочную функцию ансамбля (Рисунок 3-24). Среднее значение

)(k

, вычисленное по

-й реализации, равно

()lim()

txtdt

®¥

. (3.36)

Если случайный процесс

{

}

)(tx стационарен, а )(k

, вычисленное по

различным реализациям согласно формуле (3.36), совпадают, то случайный

процесс называется эргодическим. Для эргодических процессов средние зна-

чения, полученные усреднением по времени (как и другие характеристики,

вычисленные усреднением по времени), равны аналогичным характеристи-

кам, найденным усреднением по ансамблю, т. е.

)( . Свойством эрго-

дичности могут обладать только стационарные процессы. (Рисунок 3-23).

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Рисунок 3-24 - Ансамбль реализаций, задающих случайный процесс

Стационарный процесс будет эргодическим, если его статистические

характеристики, полученные осреднением по ансамблю, с вероятностью,

близкой к единице, равны тем же характеристикам, полученным осреднением

по времени из любой достаточно длинной реализации случайного процесса.

При нарушении этого условия колебательный процесс будет неэргодическим.

Другими словами, эргодическим называется случайный стационарный

процесс, для которого результаты усреднения по времени в пределах отдель-

ной реализации одинаковы для всех реализаций. Таким образом, усреднение

по времени для любой отдельной реализации эквивалентно соответствующе-

му усреднению по ансамблю реализаций.

Очевидно, что случайные эргодические процессы образуют очень важ-

ный класс случайных процессов, поскольку все свойства эргодических про-

цессов можно определить по единственной выборочной функции. На практи-

ке случайные стационарные процессы обычно оказываются эргодическими.

Именно по этой причине свойства случайных стационарных явлений часто

можно определить по одной наблюдаемой реализации.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Для любой реализации )(tx

случайного стационарного процес-

са

{

}

)(tx

, где

,...

- номер реализации, средний квадрат определяется

равенством

lim()

xxtdt

®¥

. (3.37)

Если процесс эргодический, то этот результат не должен зависеть от

и будет одним и тем же для всех реализаций. Соответствующее среднее по

ансамблю значение определяется равенством

lim()

Exxt

®¥

éù

ëû

и в случае стационарного процесса не зависит от

. Для эргодического про-

цесса оба усреднения дают одинаковый результат.

В общем случае результаты усреднения по любой отдельной реализа-

цииопроцесса не характеризуют свойство ни одной из его реализаций, по-

скольку информация о зависимости свойств процесса от времени в результа-

те такого усреднения утрачивается.

Говорят, что случайный процесс эргодичен, если с вероятностью, рав-

ной единице, все его статистические характеристики можно предсказать по

одной реализации из ансамбля с помощью усреднения по времени. Иными

словами, средние значения по времени почти всех возможных реализаций

процесса с вероятностью единица сходятся к одной и той же постоянной ве-

личине - среднему значению по ансамблю

3.13. Нестационарные случайные процессы

Необходимо заметить, что в общем случае строго стационарных про-

цессов в природе нет. Считать процесс стационарным или нестационарным -

зависит в основном от выбора продолжительности времени наблюдения.

К нестационарным процессам относятся все случайные процессы, не-

удовлетворяющие условиям стационарности. Если не наложены дополни-

тельные ограничения, то свойства случайных нестационарных процессов

обычно зависят от времени и могут быть установлены только путем усредне-

ния в отдельные моменты времени по ансамблю выборочных функций, обра-

зующих процесс. На практике часто не удается получить достаточное для

точной оценки свойств процесса число реализаций. Этим фактом объясняет-

ся отставание в развитии практических методов измерения и анализа случай-

ных нестационарных процессов.

Во многих случаях случайные нестационарные процессы, отвечающие

реальным физическим явлениям, имеют особенности, упрощающие их ана-

лиз и измерение. Так, большой класс случайных нестационарных колеба-

тельных процессов, у которых хотя бы одна статистическая характеристика

зависит от времени, можно представить в виде суммы

()()()()

xttxtxt

, (3.38)

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

где )(tx

- случайный стационарный процесс;

)

(

()

- неслучайные

функции времени, причем

()

является математическим ожиданием

)

(

Случайные колебания со слагаемым

()

в виде детерминированной

функции времени и при

)

(

относятся к нестационарным по матема-

тическому ожиданию колебательным процессам. Обычно детерминирован-

ная составляющая

()

, называемая трендом, рассматривается как нежела-

тельная компонента, искажающая наблюдения. Для исключения тренда ис-

пользуются специальные методы фильтрации и сглаживания [11]. Если )(tx

рассматривается как поме-ха, а

()

- как полезный сигнал, то такие помехи

иногда называют аддитивными, т. е. суммируемыми с сигналом. Колебатель-

ный процесс, нестационарный по дисперсии, определяется формулой (3.37)

при условии, что

()

xtconst

, а

)

(

- детерминированная функция времени.

Такие случайные процессы иногда называют мультипликативными. Процес-

сы, нестационарные по спектральной плотности (корреляционной функции),

изменяют свои частотные свойства во времени, а колебательные процессы,

нестационарные по одномерной плотности распределения, изменяют во вре-

мени свои законы распределения. Кроме указанных, возможны колебатель-

ные процессы с более сложными видами нестационарности, а также комби-

нированные нестационарные процессы.

Нестационарным называется любой процесс, не обладающий свойст-

вом стационарности. Статистические характеристики такого процесса, опре-

деленные усреднением по ансамблю его реализаций, не являются инвариант-

ными по отношению к переносу начала отсчета на временной оси и зависят

от времени.

Другими словами, данные представляются случайным нестационарным

процессом, если все выборочные функции которого имеют общий детерми-

нированный тренд. Если случайный нестационарный процесс имеет такой

вид, то для описания его свойств не всегда требуется усреднение по ансамб-

лю. Иногда многие важные свойства удается оценить по единственной выбо-

рочной функции, как и в случае эргодических стационарных процессов.

3.14. Стационарность выборочных функций

Понятие «стационарность», введенное и рассмотренное ранее, относит-

ся к средним по ансамблю свойствам случайного процесса. Однако на прак-

тике часто говорят о стационарности или нестационарности данных, пред-

ставляющих собой единственную реализацию случайного явления. В этом

случае стационарность понимается в несколько ином смысле. Если о единст-

венной реализации говорят как о стационарной, то обычно имеют в виду, что

ее свойства, определенные на коротких интервалах времени, существенно не

изменяются от интервала к интервалу. Слово «существенно» означает здесь,

что наблюдаемые колебания превосходят отклонения, которые можно объяс-

нить обычной выборочной изменчивостью статистических оценок.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

3.15. Анализ случайных данных

Анализ случайных данных основан на иных соображениях, чем анализ

детерминированных данных. В частности, в силу того, что реализацию

случайного процесса нельзя задать явной математической формулой, для

оценки свойств таких данных должны использоваться статистические

методы. Тем не менее, случайные процессы удовлетворяют вполне

определенным соотношениям, описывающим преобразования этих

процессов; эти соотношения играют ключевую роль во многих приложениях.

В таких приложениях важно уметь выявлять и учитывать статистические

ошибки, связанные с оценками параметров и соотношениями между

входными и выходными процессами преобразований.

При обсуждении интуитивных предпосылок теории целесообразно рас-

смотреть описательные определения этих величин, не прибегая к математи-

ческим формулам, а в качестве примеров рассмотреть некоторые особенно

интересные частные случаи (Рисунок 3-25).

3.16. Основные характеристики случайных процессов

Основные статистические характеристики, имеющие важное значение

для описания свойств отдельных реализаций случайных стационарных про-

цессов, таковы:

1) средние значения и средние квадраты;

2) плотности вероятности;

· проверки нормальности;

· выявления нелинейностей;

· анализа экстремальных значений.

3) ковариационные функции;

· выявление периодичностей;

· выделение сигналов из шума;

· измерение запаздываний;

· локализацию источников помех:

· идентификацию трактов и скоростей распространения сигналов.

4) функции спектральной плотности.

· определение свойств систем по наблюдениям входных и выход-

ных процессов:

· предсказание выходных процессов по входным процессам и

свойствам системы;

· идентификация входных процессов по выходным процессам и

свойствам системы;

· задание динамических данных для тестовых программ;

· идентификация источников энергии и шума;

· оптимальный линейный прогноз и фильтрация.

Для пар реализаций, принадлежащих двум разным случайным стацио-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

нарным процессам, важное значение имеют совместные статистические ха-

рактеристики, а именно:

5) совместные плотности вероятности;

6) взаимные ковариационные функции;

7) взаимные спектральные плотности;

8) частотные характеристики;

9) функции когерентности.

Первые три функции описывают основные свойства пары реализаций

по принимаемым ими значениям и по их свойствам во временной и частот-

ной областях. По известным взаимной спектральной плотности и спектраль-

ным плотностям реализаций можно теоретически вычислить линейные час-

тотные характеристики (амплитудные и фазовые характеристики), связы-

вающие эти две реализации. В этом случае реализации считаются входом и

выходом некоторой линейной системы. Функция когерентности характеризу-

ет точность принятой линейной модели и тоже может быть вычислена по из-

мерениям спектральной и взаимной спектральной плотностей.

3.17. Вероятностные характеристики процессов

Случайные процессы описываются с помощью плотности вероятности

или функции распределения и моментов распределения. Плотность вероят-

ности

)

(

в моменты времени

задается отношением

WxP

),(

)( = ,

где

)

(

– вероятность попадания значения

)

(

в интервал шириной

центром в точке

. Иными словами,

)

(

- есть оценка интенсивности изме-

нения вероятности значения функции

)

(

Плотность вероятности

)

(

стационарной реализации задает скорость

изменения вероятности в зависимости от значения реализации. Функция

)

(

обычно оценивается путем вычисления вероятности того, что мгновен-

ное значение отдельной реализации заключено в узком интервале, центр ко-

торого пробегает область значений процесса, с последующим делением на

ширину интервала. Общая площадь, ограниченная графиком плотности веро-

ятности по всей его области определения, равна единице. Это свидетельству-

ет о достоверности события, заключающегося в том, что значения реализа-

ции содержатся между

. Часть этой площади, лежащая левее дан-

ного значения х, определяет функцию распределения, обозначаемую

)

(

Часть площади, ограниченная графиком плотности между произвольными

двумя значениями

x и

x и равная )(

xP - )(

xP , задает вероятность того,

что значения реализации в наугад выбранный момент времени попадут в этот

интервал значений процесса (Рисунок 3-26).