Костюков В.Н., Науменко А.П., Бойченко С.Н., Тарасов Е.В. Основы виброакустической диагностики машинного оборудования

Подождите немного. Документ загружается.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

моногармонические колебания, при которых колеблющаяся величина изме-

няется по закону

()cos()

xtCt

=××+

. (3.13)

Спектр моногармонического колебания содержит только одну наблю-

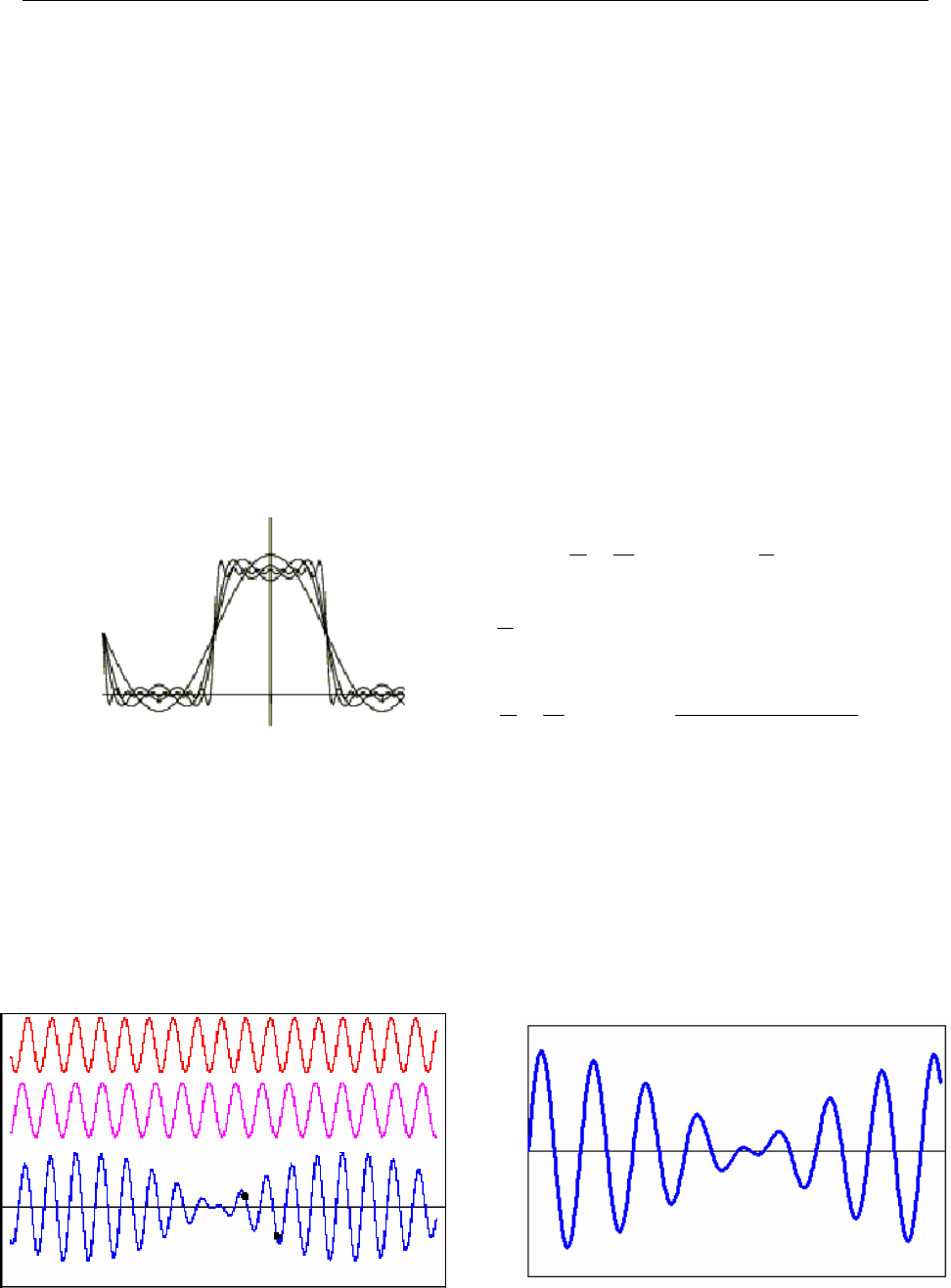
даемую частоту (Рисунок 3-5). Полигармонический колебательный процесс

(Рисунок 3-12) может быть представлен в виде суммы нескольких моногар-

монических колебаний с частотами, находящимися между собой в рацио-

нальном отношении:

()cos()

xtCt

kkk

=××+

. (3.14)

Форма графика изменения колеблющейся величины во времени в зави-

симости от соотношения параметров

гармоник позволяет провести клас-

сификацию процессов, разделяя их на прямоугольные, пилообразные, трапе-

цеидальные и т.д. колебания.

121

()(coscos3

cos5...)

12cos(21)

(1)

221

Sxxx

=+×-××+

+××+=

×-×

=+-

Рисунок 3-12 - Полигармонический колебательный процесс

Частный случай полигармонических колебаний - это бигармонические

колебания, состоящие из суммы двух моногармонических колебаний

(Рисунок 3-13):

111222

()cos()cos(),

xtAtAt

wjwj

=×++×+

(3.15)

угловые частоты которых

находятся между собой в рациональном

соотношении.

Рисунок 3-13 – Биения

Вид бигармонического колебательного процесса зависит не только от

соотношения между частотами и амплитудами обеих гармоник, но и от фазо-

вых соотношений. При достаточной близости частот колебаний будут на-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

блюдаться характерные биения процесса, при которых его полуразмах мед-

ленно изменяется в пределах от )(

1212min

AAAAA

до

max

AAA

Таким образом, биение - это результат сложения двух колебаний с

близкими частотами.

Преимущества полигармонической модели возбуждения колебаний в

том, что она позволяет сконцентрировать внимание лишь на определенных

частотах

, кратных основной частоте возбуждения колебаний

диагно-

стируемого узла, поскольку процесс локализации источников повышенной

виброактивности агрегата состоит в выявлении источников возбуждения, вы-

зывающих колебания на данной частоте.

Квазиполигармоническая модель процесса возбуждения колебаний

основана на представлении колебаний в виде суперпозиции узкополосных

случайных процессов с кратными средними частотами. Квазиполигармони-

ческая модель более адекватно описывает процесс возбуждения колебаний,

чем полигармоническая. Размытие линий спектра квазиполигармонической

модели колебаний по отношению к дискретным составляющим полигармо-

нической модели не является недостатком.

3.5. Спектр сигнала

Спектральный анализ - один из методов обработки сигналов, который

позволяет охарактеризовать частотный состав измеряемого сигнала. Преоб-

разование Фурье является математической основой, которая связывает вре-

менной сигнал (или же некоторую модель этого сигнала) с его представлени-

ем в частотной области. Важную роль в спектральном анализе играют мето-

ды статистики, поскольку виброакустические сигналы, как правило, пред-

ставляют собой смесь шумовых и периодических составляющих. Поэтому по

отрезку сигнала можно получить только оценку его спектра.

В основе преобразования Фурье (ПФ) лежит чрезвычайно простая, но

исключительно плодотворная идея – почти любую периодическую функцию

можно представить суммой отдельных гармонических составляющих (сину-

соид и косинусоид с различными амплитудами

, периодами

(частотами

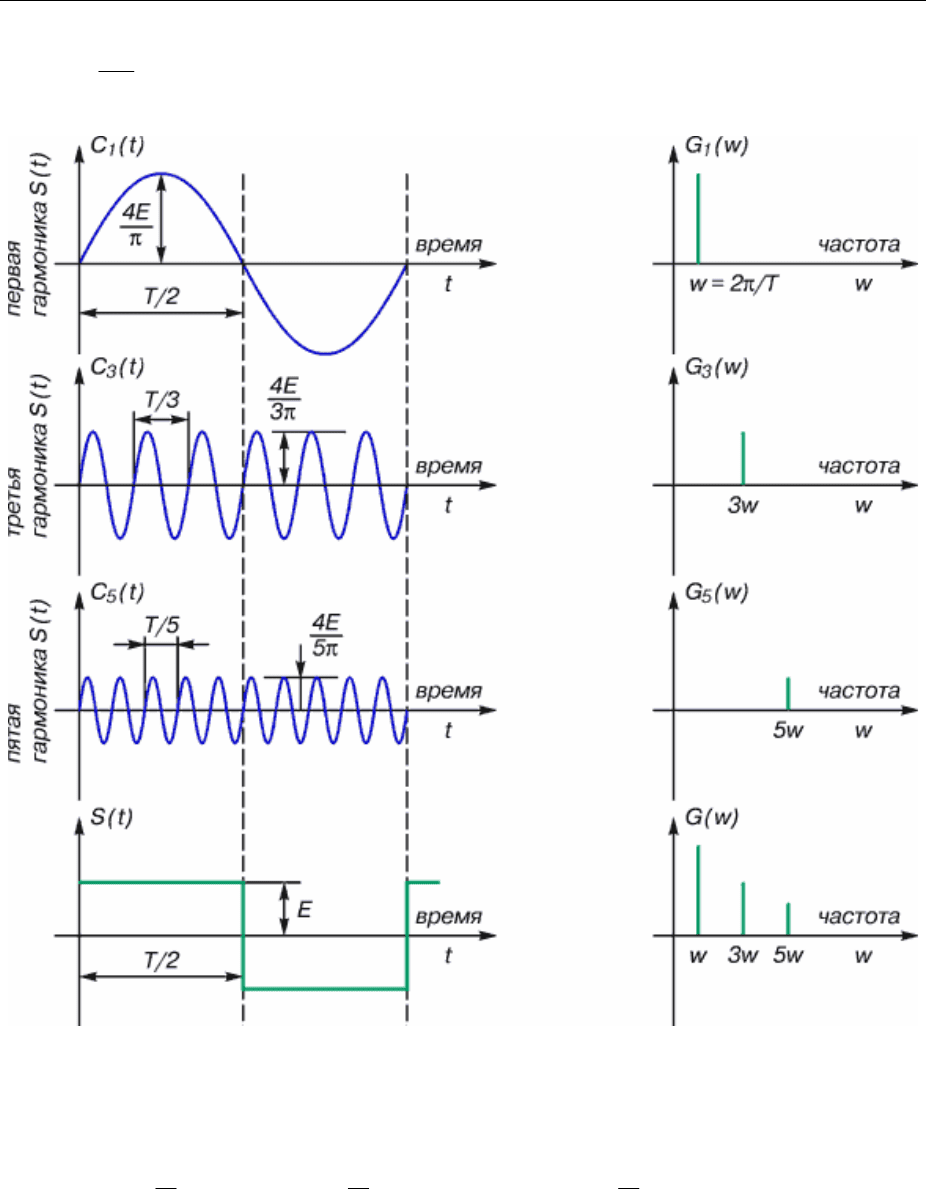
)) (рис. 3.12, 3.14). Нижняя часть последнего рисунка есть иллюстрация од-

ного из основных принципов ПФ – спектр суммарной функции времени ра-

вен сумме спектров ее гармонических составляющих.

Если

()

– периодическая функция с периодом

, так что

()()

ststT

, а также являющаяся непрерывной на этом интервале или

имеющая конечное сило разрывов первого рода (т.е. функция

()

должна

иметь конечные пределы) и имеющая на интервале

конечное число макси-

мумов и минимумов, то ее можно представить бесконечной суммой тригоно-

метрических функций

()(cossin)

kkkk

stsatbt

=++

, (3.16)

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

где

= ;

- длительность сигнала;

,1,2,3,...

=×=

Рисунок 3-14 - Представление прямоугольного импульса

суммой гармонических составляющих

Коэффициенты

определяются по формулам:

000

222

(),()cos(),()sin()

TTT

kkkk

sstdtasttdtbsttdt

TTT

===

òòò

Согласно этим формулам, коэффициенты

являются скалярны-

ми произведениями функции

()

на функции t

cos и t

sin , т.е. служат

проекциями вектора

()

на координатные оси, ортами которых служат ука-

занные тригонометрические функции.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Любую гармонику ряда Фурье можно представить в виде амплитуды

(модуля) и начальной фазы

(аргумент). Для этого коэффициенты ряда

следует записать в виде

cos,sin

kkkkkk

acbc

так что

kkk

cab

,()

kkkkkk

tgbaarctgba

. (3.17)

Тогда соотношение (3.16) можно записать в другом виде:

()cos()

kkk

stsct

=+-

, (3.18)

где

- начальная фаза;

-й гармоники сигнала;

- ее амплитуда.

Совокупность чисел

называют амплитудным спектром, а числа

- спектром его фаз. Из приведенных соотношений видно, что в общем слу-

чае периодический сигнал содержит не зависящую от времени постоянную

составляющую

и бесконечный набор гармонических колебаний, так назы-

ваемых гармоник с частотами

,1,2,3,...

=×=

, кратными основной

частоте

Применив формулы Эйлера в ряд (3.16) можно представить в экспо-

ненциальном виде

()()

itititit

kkkk

eeee

stsab

wwww

=++

или

()

stCe

=-¥

, (3.19)

где

()22,()22,2||,

kkkkkkkkkk

CaibceCaibcecCcC

=-==+===

Комплексный спектр C

можно выразить и с помощью интеграла

()

Cstedt

. (3.20)

Спектр является важнейшей характеристикой сигнала и отражает все

его свойства. Зная спектр можно восстановить сигнал. В этом смысле пред-

ставления сигнала в виде функции времени и в форме спектра (в виде функ-

ции частоты) равнозначны. Но для решения конкретной задачи бывает удоб-

нее то или другое представление сигнала, поэтому рассматривают его в двух

аспектах: во временном и спектральном.

Говоря о равнозначности спектра и временной формы сигнала, подра-

зумевают комплексный спектр, т.е. спектр амплитуд и фаз. На практике, го-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

воря о спектре, чаще всего имеют в виду спектр амплитуд. По спектру ам-

плитуд нельзя восстановить первоначальную форму сигнала, однако ампли-

тудный спектр обычно вскрывает такие свойства сигнала, ради которых и

прибегают к спектральному представлению.

Следует отметить, что формулы (3.17), (3.19) и (3.20) справедливы

только для периодических сигналов. Но это ограничение несущественно (и

это можно доказать в достаточно строгой форме). Поскольку любой сигнал

)

(

существует на конечном интервале времени

и интересует его

форма только на этом интервале, то ничто не мешает считать его периодиче-

ским вне указанного интервала. Можно предположить, что

()().

ststT

(3.21)

Интервал

)

(

, на котором задан сигнал, рассматривается как один из

его периодов, вне которого форма сигнала повторяется. Но возможен и дру-

гой подход, при котором считается, что до момента времени

сигнала не

было, вернее он был равен нулю, а также и после момента

он стал равен

нулю. При таких предположениях суммы в формулах (3.17) и (3.19) следует

заменить интегралами. Ряд (3.19) переходит в интеграл

()()

stSed

-¥

, (3.22)

а формула (3.20), выражающая спектр сигнала, принимает вид

()()

Sstedt

. (3.23)

В общем случае, когда не уточнено значение

, спектральная плот-

ность записывается в виде

()()

Sstedt

-¥

. (3.24)

Соотношения (3.22) и (3.23) являются соответственно прямым и обрат-

ным преобразованием Фурье. Функция

)

(

называется спектральной

плотностью. Ее модуль )(

S характеризует распределение интенсивности

гармонических составляющих сигнала

)

(

по частотам. Величина

dS )(

соответствует амплитуде синусоидального колебания с частотой

, содер-

жащегося в сигнале

)

(

3.6. Модуляция колебаний

К более сложным видам колебаний относятся модулированные колеба-

тельные процессы

()()sin(()())()cos(),

stAttttAtt

wjy

=+=

(3.25)

у которых один либо несколько параметров изменяются во времени. В зави-

симости от того, какой из трех параметров периодически изменяется, разли-

чают амплитудно-модулированные (АМ), частотно-модулированные (ЧМ) и

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

модулированные по фазе (ФМ) периодические колебания. В большинстве

случаев эти параметры изменяются настолько медленно, что в пределах од-

ного периода колебательный процесс можно считать гармоническим.

Во время работы в результате соударения деталей в механизме возбуж-

даются колебания на собственных частотах. Эти частоты являются констан-

тами механизма и не меняются при изменении его состояния. Поэтому само

синусоидальное колебание на собственной частоте не несет диагностической

информации. Выделение одной из собственных частот

, называемой несу-

щей, позволяет оценить структуру колебания на этой частоте. Это колебание

можно записать в следующем виде:

()()sin(()),

stAttt

=×+

(3.26)

т.е. амплитуда и фаза этого гармонического колебания меняются со временем

по определенному закону. Изменения амплитуды связаны с тем, что в мо-

мент удара в материал механизма передается определенная порция энергии и

амплитуда упругих колебаний скачком увеличивается до значения

. Затем

энергия колебаний постепенно рассеивается и их амплитуда уменьшается по

экспоненциальному закону

. К моменту очередного удара амплитуда ко-

лебаний уменьшается до

, после чего материал снова получает порцию

энергии. Изменение амплитуды называют модуляцией, а разность между

наибольшим и наименьшим значением амплитуды, отнесенную к наиболь-

шей амплитуде, называют глубиной модуляции и обозначают

. (3.27)

Глубина модуляции зависит от периода следования ударов

и вели-

чины коэффициента затухания

. Функция

)

(

, соответствующая изме-

нению амплитуды синусоидального колебания, называется огибающей

сигнала. Ее параметры зависят от интенсивности соударения деталей, часто-

ты следования и фазы импульсов. В момент соударения деталей меняется не

только амплитуда, но и фаза колебаний. Согласно высказанным выше сооб-

ражениям, изменение амплитуды носит пилообразный характер. Но прежде

чем рассмотреть этот случай, положим, что амплитуда синусоиды

sin()

меняется также по синусоидальному закону, но со значительно меньшей час-

тотой, чем

. Итак

()(1sin)sin()

stARtt

=-×W×××+

, (3.28)

причем 1,

£W>> R

Раскрывая скобки, получим

000000

()sin()cos()cos().

stAttt

wjwjwj

ìü

=×++-W+-+W+

éùéù

íý

ëûëû

îþ

(3.29

)

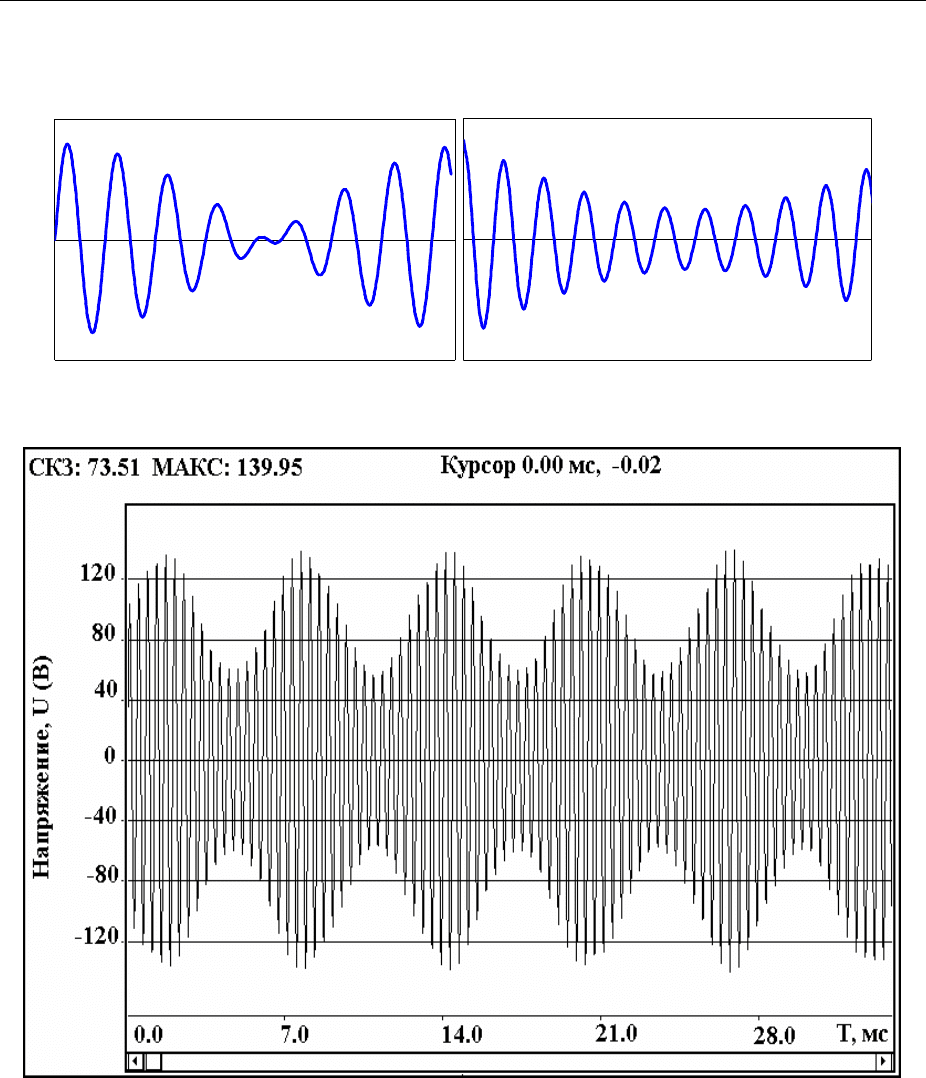
Амплитудно-модулированный (АМ) сигнал (Рисунок 3.16, 3.15 б) в

отличие от весьма похожих по виду биений (Рисунок 3.15 а) состоит из трех

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

гармонических составляющих (Рисунок 3.17), одна из которых имеет частоту

несущей

, а две другие называют боковыми: )(

и )(

а) б)

Рисунок 3-15 - Биения и амплитудная модуляция

Рисунок 3-16 - Временная реализация

амплитудно-модулированного сигнала

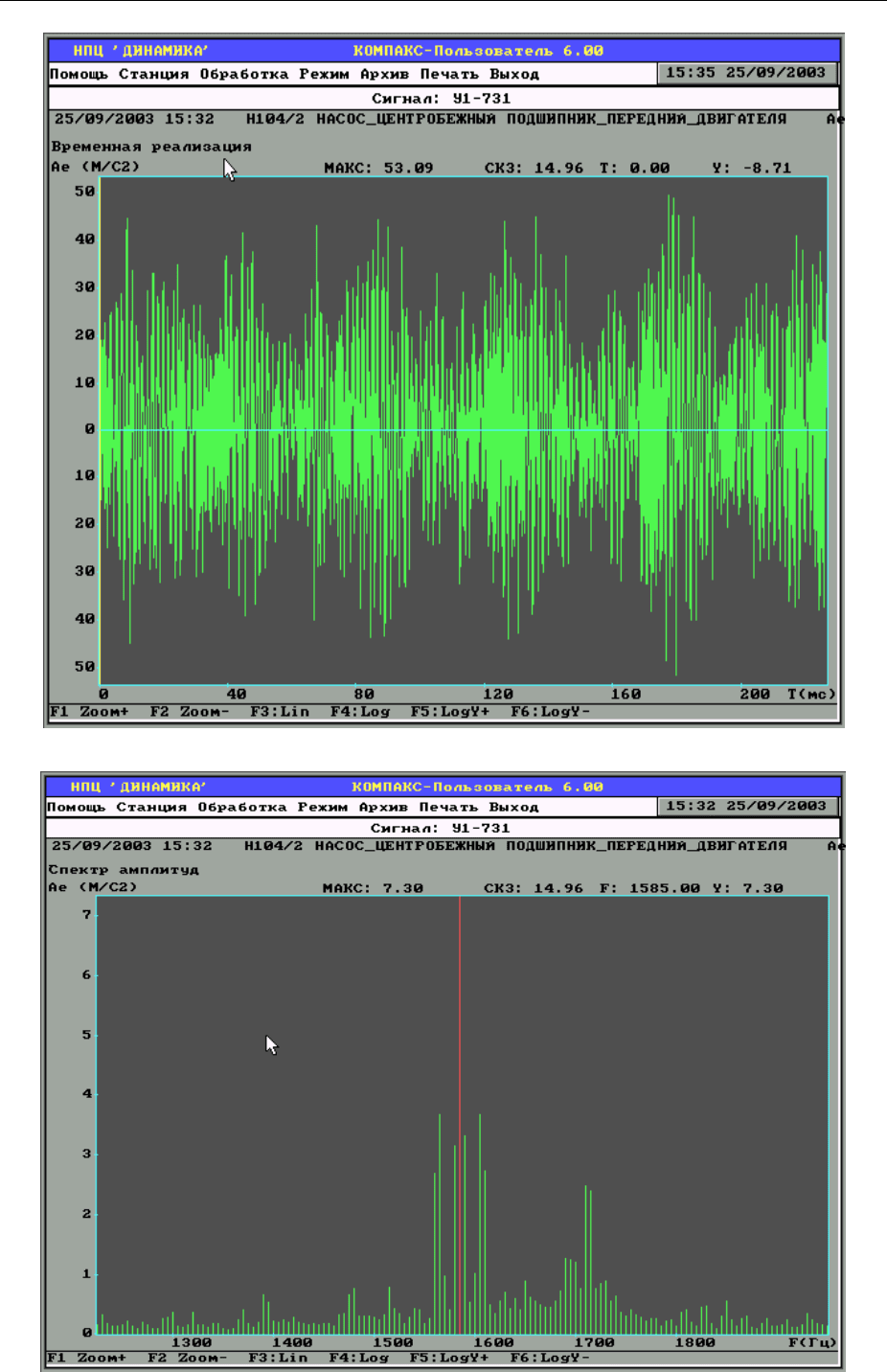
По виду временной реализации виброакустического сигнала часто

трудно отличить биения от модуляции (Рисунок 3-18) и только спектральный

анализ позволяет однозначно оценить характер сигнала (Рисунок 3-19).

В более сложном случае, когда амплитуда меняется по произвольному

закону

)

(

, эту функцию можно разложить на гармонические составляющие

и рассмотреть модуляцию каждой составляющей в отдельности.

Спектр модулированного колебания будет иметь спектральную линию

на частоте несущей

и, симметрично расположенные по отношению к ней,

боковые полосы (Рисунок 3-17, Рисунок 3-19), в точности соответствующие

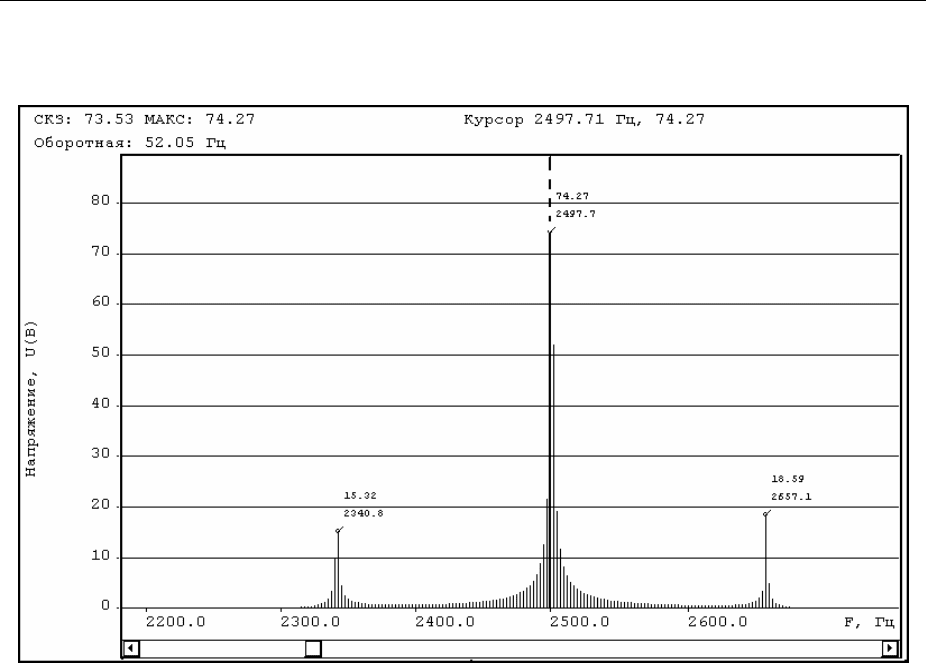
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

спектру огибающей

)

(

. Поэтому задача определения спектра модулиро-

ванного колебания сводится к задаче нахождения спектра его огибающей.

Рисунок 3-17 - Спектр АМ сигнала

Модуляция – это изменение какого-то параметра одного сигнала под

влиянием другого сигнала и - это нелинейный процесс, который может про-

изойти только при взаимодействии двух или более сигналов. В механических

системах часто происходит амплитудная и частотная модуляции различных

компонент силовых взаимодействий, в результате чего в спектре вибрации

появляются боковые полосы.

Примером частотно-модулированного (ЧМ) колебания является про-

цесс вида

(

)

000

()coscos,

stAtt

wwj

éù

=×+D×W×+

ëû

(3.30)

где

- величина частотного отклонения, называемая девиацией частоты

или просто девиацией;

- частота гармонической модуляции.

Амплитуда такого процесса не меняется во времени, а частота изменя-

ется по гармоническому закону относительно некоторой несущей частоты

Спектр ЧМ колебания значительно сложнее, чем спектр АМ колебания. При

очень малых девиациях

)

(

спектр содержит одну центральную и

две боковые линии )(),(

, имеет ширину

. При возрастании

девиации частот

)

(

приобретает некоторую значимость вторая

пара боковых частот, поэтому ширина спектра возрастает до

При увеличении девиации спектр будет включать все новые значимые

пары кратных частот. При

)

(

ширина спектра ЧМ колебания близ-

ка к удвоенной девиации частоты

, а число линий в спектре будет столь

велико, что он может быть ошибочно принят за непрерывный спектр.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Рисунок 3-18 – Амплитудно-модулированный вибросигнал

Рисунок 3-19 – Спектр амплитудно-модулированного вибросигнала

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Модулированные по фазе колебания тесно связаны с частотно-

модулированными колебаниями, поскольку угловая частота есть не что иное,

как скорость изменения фазы колебания:

()()/

ttdt

()()

ttdt

jwj

. (3.31)

В случае гармонической модулирующей функции по виду колебатель-

ного процесса и по его спектру нельзя заключить, с какой модуляцией имеем

дело - частотной или фазовой. Различие между ними проявится лишь в ре-

зультате изменения частоты модуляции. При частотной модуляции величина

девиации

не изменится, а при фазовой модуляции изменение

будет

прямо пропорционально изменению частоты модуляции

. В действитель-

ности, исследуемые колебательные процессы часто являются модулирован-

ными одновременно как по амплитуде, так и по частоте (фазе). При этом

обычно нарушается симметрия спектра, но отличить один вид сложной мо-

дуляции от другого при помощи анализа спектров весьма трудно, а часто и

невозможно.

3.7. Демодуляция колебаний

Современные методы теории аналитического сигнала [16] позволяют

выделить (демодулировать) из колебательного процесса его мгновенную ам-

плитуду (огибающую)

)

(

, мгновенную фазу

)

(

и мгновенную частоту

)

(

. Для получения этих мгновенных функций необходимо с помощью ин-

тегрального преобразования Гильберта преобразовать исходный процесс

()

, заданный на интервале

-¥<<¥

, в сопряженный процесс

()

[16]:

()

()[()]

()

xt Гxtdu

-¥

где интеграл понимается в смысле главного значения.

Преобразование Гильберта можно осуществить, например, если на

вход фильтра с импульсной характеристикой

)(

подать сигнал, опреде-

ляемый функцией

)

(

.[16]:

()()*()

xttxt

=×

, (3.32)

где знаком * обозначена свертка функций

)(

)

(

Физический смысл интегрального преобразования Гильберта для сиг-

нала, представленного в частотной области, заключается в фазовом сдвиге

всех спектральных составляющих исходного сигнала на

. Двойное пре-

образование Гильберта приводит к исходному процессу, но только с обрат-

ным знаком, т. е. осуществляет сдвиг исходного сигнала на

Используя понятие аналитического сигнала

()()()()cos()

XtxtjxtAtt

=+=

, (3.33)

можно однозначно определить мгновенные амплитуду (огибающую), фазу и

частоту процесса [16, 27]: