Костюков В.Н., Науменко А.П., Бойченко С.Н., Тарасов Е.В. Основы виброакустической диагностики машинного оборудования

Подождите немного. Документ загружается.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

2.1. Общая постановка задачи диагностирования

Состояние объекта, которое определяется n независимыми величинами

,,...,

xxx

, в некоторый момент времени

известно, если известно значение

каждой из

величин

x . Эта задача будет также решена и в том случае, если

будут выражены через какие-то другие величины

,,...,

sss

, которые из-

вестны. Такой косвенный процесс определения неизвестных параметров

x и

называют диагностикой. Она сводится к измерению параметров диагности-

ческого сигнала

,,...,

sss

и к вычислению параметров состояния

x с помо-

щью известных заранее соотношений вида:

(,,...,)

iim

xXsss

(2.1)

Конкретный вид функции (2.1) определяется либо во время тарировки

системы диагностики, либо на основе моделирования объекта, либо путем

установления экспериментальных зависимостей.

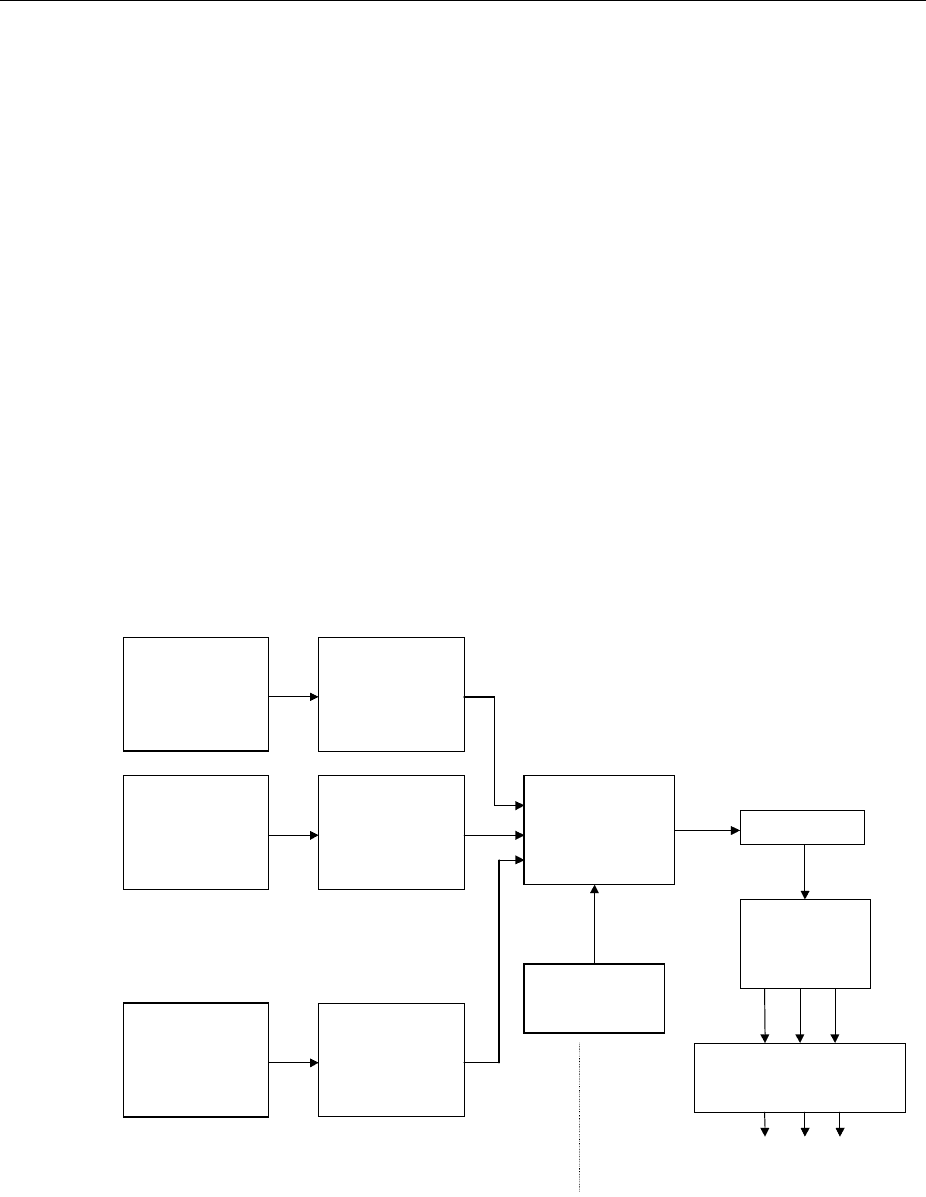
В основе виброакустической диагностики лежит почти тривиальная

идея о представлении объекта в виде многоканальной системы передачи ин-

формации (Рисунок 2-1).

Источник

информации

(кинематичес-

кая пара)

Кодер

(кинематичес-

кая пара)

Источник

информации

(кинематичес-

кая пара)

Кодер

(кинематичес-

кая пара)

Источник

информации

(кинематичес-

кая пара)

Кодер

(кинематичес-

кая пара)

Среда

(акустический

канал)

Источник

помех

Датчик

Блок

разделения

сигналов

Блок измерения

параметров сигнала

Диагностируемый механизм Диагностическая аппаратура

Рисунок 2-1 – Объект (механизм, содержащий кинематические пары) как

многоканальная система передачи информации

Представление объекта в виде многоканальной системы передачи ин-

формации позволяет сформулировать две основные проблемы, решение ко-

торых составляет предмет технической диагностики, а также позволяет ис-

пользовать в диагностике методы и опыт организации и функционирования

систем многоканальной передачи информации. Проблемы эти следующие:

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

а) необходимо найти способы разделения сигнала, полученного с дат-

чика, на такие составляющие, каждая из которых принадлежит только одно-

му источнику виброакустического сигнала;

б) необходимо по этой составляющей оценить состояние соответст-

вующего источника виброакустического сигнала.

Эффективность процессов постановки диагноза определяется не только

качеством алгоритма диагноза, но и не в меньшей степени качеством средств

диагностики. Эффективная организация системы сбора и обработки инфор-

мации, увеличивающая достоверность диагностики, уменьшающая влияние

субъективных факторов, а также сокращающая затраты времени, труда и

средств, включает разработку автоматизированной системы виброакустиче-

ской диагностики сложного объекта на стадии его проектирования как необ-

ходимую составную часть объекта.

Проведение виброакустического диагностирования связано с решением

ряда взаимосвязанных задач:

1) детальным изучением объекта с целью выявления наиболее уязви-

мых мест, составлением перечня параметров

,,...,

xxx

, выходящих за до-

пустимые нормы, и разбиением на классы технических состояний, подлежа-

щих распознаванию;

2) выбором средств измерения и мест размещения первичных преобра-

зователей на объекте на основе изучения физики процессов, протекающих в

объекте;

3) локализацией источников излучения повышенной колебательной

энергии в исследуемом объекте;

4) определением динамических характеристик и математических моде-

лей отдельных узлов и объекта в целях построения диагностической модели;

5) формированием и доводкой системы информативных диагностиче-

ских признаков, чувствительных к изменению параметров технического со-

стояния в процессе обучения диагностической системы;

6) разработкой алгоритмов определения текущего состояния объекта;

7) прогнозированием изменений виброакустического сигнала и пара-

метров технического состояния;

8) разработкой процедур обратного воздействия на объект (выключе-

ние, перевод на щадящий режим и т.д.).

2.2. Основные задачи диагностики

Техническая диагностика изучает методы получения и оценки диагно-

стической информации, диагностические модели и алгоритмы принятия ре-

шений. Целью технической диагностики является повышение надежности и

ресурса технических систем.

В общем виде задачу диагностирования допустимо рассматривать как

двойственную задачу: задачу построения характеристики класса состояний,

которому принадлежит совокупный виброакустический образ, и задачу при-

нятия решения о принадлежности к одному из классов состояний испытуемо-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

го виброакустического образа. При этом следует учитывать, что увеличение

числа зависимых диагностических признаков не способствует более полно-

му описанию объекта диагностирования и надежному распознаванию.

Диагностика как наука о распознавании состояния технической систе-

мы определяет следующие основные задачи в области диагностирования со-

стояния машинного оборудования [8, 13, 102, 18 - 26, 51, 56, 64, 78, 85]:

- определение технического состояния, в котором находится оборудо-

вание в прошлом (генезис), настоящем (диагноз) и будущем (прогноз);

- поиск места и определение причин неисправности;

- контроль технического состояния, т.е. определение вида техническо-

го состояния. Видами технического состояния являются исправное и неис-

правное, работоспособное и неработоспособное и т.д.

Решение этих задач необходимо для организации технического

обслуживания оборудования по фактическому техническому состоянию,

вместо обслуживания по ресурсу. Кроме того, это позволяет реализовать

безопасную ресурсосберегающую эксплуатацию оборудования всех отраслей

промышленности.

2.3. Функциональная схема технического диагностирования

Алгоритм виброакустического диагностирования может быть пред-

ставлен в виде функциональной схемы (Рисунок 2-2) [18].

Как и любой алгоритм или схема распознавания образов, схема виб-

роакустического диагностирования технического объекта состоит из собст-

венно объекта диагностирования с набором технических состояний, подле-

жащих распознаванию, набора диагностических признаков, решающих пра-

вил и правил принятия решения.

Управление

объектом

Объект

диагностики

Измерение

виброакусти-

ческих

параметров

Формирование

диагностических

признаков

Класси-

фикация

Диагноз

Диагностическая

модель

Формирование

эталонов

Набор решающих

правил

Рисунок 2-2 - Функциональная схема

системы виброакустической диагностики.

Измерение обеспечивает исходной информацией о состоянии объекта,

содержащуюся в измеряемых сигналах.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Формирование диагностических признаков технического состояния

объекта и отдельных его элементов позволяет выделить такие характеристи-

ки измеряемых сигналов, которые обладают требуемыми избирательными

свойствами к заданному классу дефектов, подлежащих распознаванию.

На основании обучения диагностической системы для каждого класса

технических состояний формируются эталоны (усредненные для данного

класса значения диагностических признаков).

Для формирования системы диагностических признаков и эталонов ис-

пользуют диагностическую модель объекта, в ряде случаев облегчающую

процесс поиска информативных компонент в исследуемом сигнале.

Классификация – набор классифицирующих функций, с помощью ко-

торых производится распознавание параметров виброакустического сигнала.

Функция принятия решений - определение фактического состояния

(постановка диагноза) объекта диагностирования и его элементов по теку-

щим значениям диагностических признаков. Характеристики изменения по-

следних во времени являются исходными для реализации алгоритмов упреж-

дения (прогноза) потенциальных отказов.

Функция управления объектом в соответствии с принятым решением о

его фактическом состоянии обеспечивает: аварийное отключение, перевод на

щадящий режим, включение резервов и т.д.

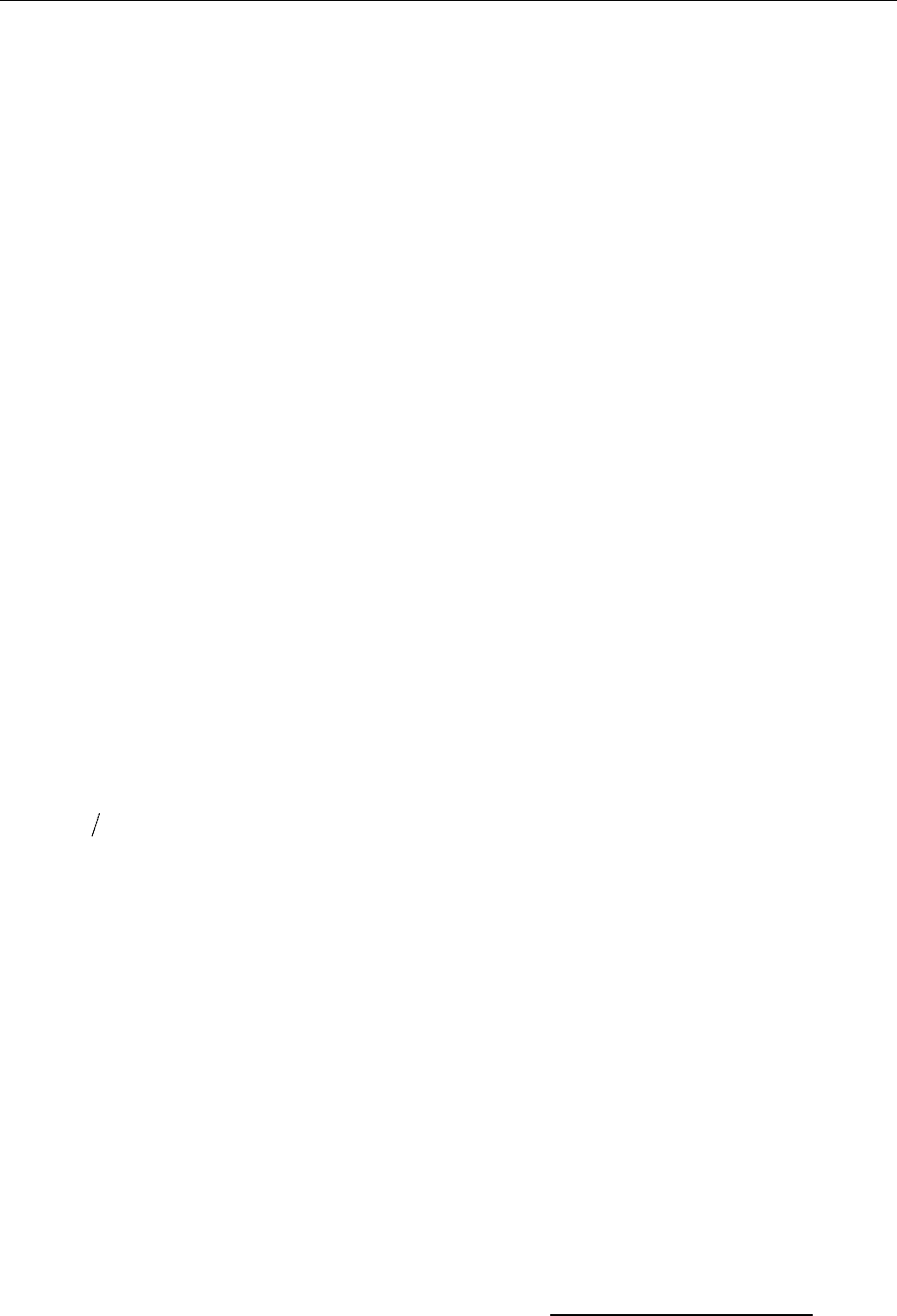
В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

3. Виброакустические колебания и сигналы

3.1. Свойства виброакустических колебаний

Информация о состоянии деталей объекта представляется сигналами. В

качестве диагностического сигнала может быть использован процесс любой

физической природы, лишь бы характер его протекания зависел от состояния

объекта и был доступен для регистрации доступными средствами. На пути от

места его возникновения, расположенного внутри объекта, до получения ре-

зультатов диагноза сигнал претерпевает многочисленные преобразования:

меняется его форма и физическая природа, единственное, что должно остать-

ся неизменным, это переносимая сигналом информация. Поэтому, прежде

чем перейти к рассмотрению чисто физических вопросов о возбуждении ко-

лебаний, об их распространении по объекту и их зависимости от его состоя-

ния, следует совершить небольшой экскурс в общую теорию колебаний и об-

работки сигналов. Это тем более необходимо сделать потому, что все про-

цессы, протекающие в объекте и в цепях диагностической аппаратуры, будем

считать сигналами и использовать для их анализа методы, которыми анали-

зируются сигналы.

3.1.1. Простейшее гармоническое колебание

Процессы, в которых, какая либо физическая величина периодически

изменяется во времени, называют колебаниями. Время одного цикла измене-

ний является периодом колебания

, а величина, обратная периоду – часто-

той

= .

Период колебаний (

) - это интервал времени, который необходим для

завершения одного цикла колебания. В зависимости от быстроты колебаний,

период измеряют в секундах, миллисекундах, микросекундах и т.д.

Частота колебаний (

) - величина обратная периоду, определя-

ет количество циклов колебания за период и измеряется в Герцах

(1 Гц=сек

-1

). Для роторных машин частота основного колебания соответству-

ет частоте вращения, которая измеряется в об/мин (мин

-1

) и определяется как:

, где

- частота в Гц, т.к. в минуте 60 секунд.

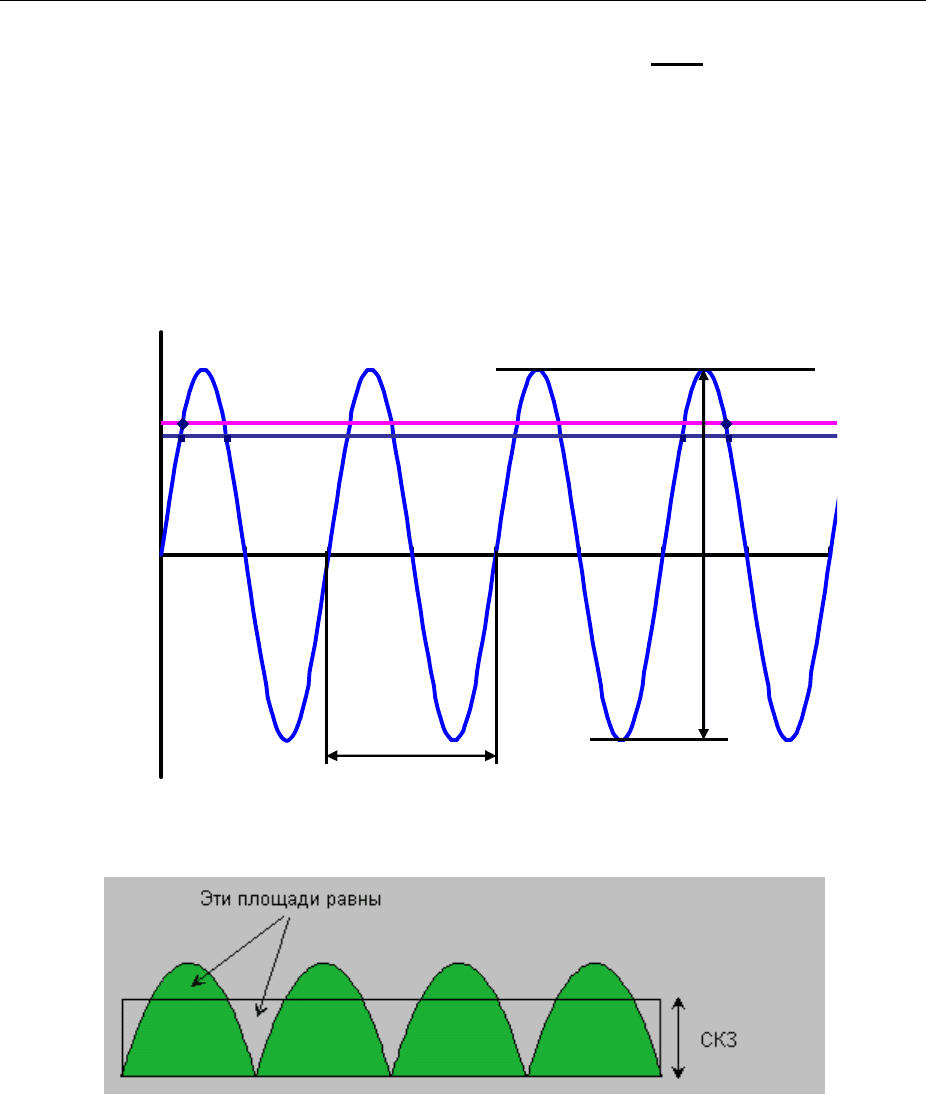
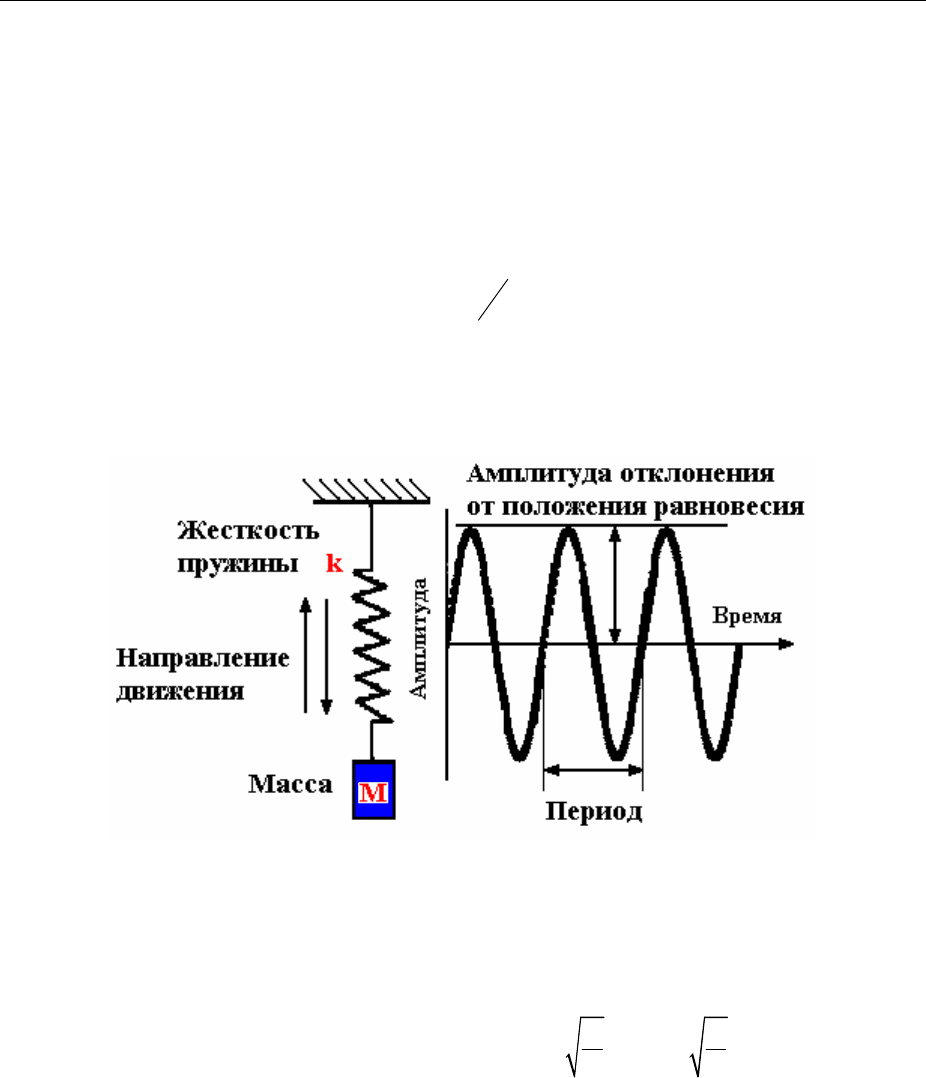
Для описания и измерения механических вибраций используются сле-

дующие понятия (Рисунок 3-1, Рисунок 3-2):

Максимальная амплитуда (Пик) - это максимальное отклонение от

нулевой точки, или от положения равновесия.

Размах (Пик-Пик) - это разность между амплитудами положительного

и отрицательного пиков. Для синусоидального колебания размах в точности

равен удвоенной пиковой амплитуде, так как временная реализация в этом

случае симметрична. Однако, в общем случае это неверно для полигармони-

ческого, случайного процессов и их смеси.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Среднеквадратическое значение амплитуды (СКЗ) равно квадратно-

му корню из среднего квадрата амплитуды колебания, т.е. для расчета СКЗ

необходимо возвести в квадрат мгновенные значения амплитуды колебаний,

и усреднить получившиеся величины по времени. Для получения правильно-

го значе-ния, интервал усреднения должен быть не меньше одного периода

колебания. После этого извлекается квадратный корень и получается СКЗ.

Для синусоидальной волны (и только для неё) СКЗ в 1,41 раза меньше пико-

вого значение, однако, такое соотношение справедливо только для данного

случая.

Среднее

СКЗ

Время

А м плитуда

Период

Размах

Пик (максимальное значение)

Рисунок 3-1 – Параметры временной реализации

Рисунок 3-2 – Среднеквадратическое значение амплитуды

По физической природе колеблющейся величины различают колебания

механические, электрические и др. Диапазон частот механических колебаний

начинается от инфразвуковых (10

-1

Гц) доходит до гиперзвуковых (10

Гц).

Самыми простыми из существующих в природе колебательных движе-

ний являются упругие прямолинейные колебания тела на пружине (Рисунок

3-3). При этом простейшая колебательная система (тело, подвешенное на

пружине) может быть описана набором параметров - массой тела

(пред-

полагается, что оно не упругое) и коэффициентом жесткости пружины (упру-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

гостью пружины)

(предполагается, что она не имеет массы). При отсутст-

вии сил сопротивления груз, смещенный от положения равновесия на вели-

чину

и предоставленный самому себе, будет совершать гармонические ко-

лебания по закону:

sin()

xSt=××+

(3.1)

где

- амплитуда колебания (максимальное смещение от положения равно-

весия);

()

×+ - фаза колебания;

- начальная фаза;

- текущее время;

- круговая (угловая) частота, равная

=××

=3,14159265359 .

В математике функция синуса описывает зависимость отношения кате-

та к гипотенузе от величины противолежащего угла. Синусоидальная кривая

при таком подходе является графиком синуса в зависимости от величины уг-

ла.

Рисунок 3-3 – Пример простейшего колебания

Период

T и круговая частота

собственных колебаний простейшей

системы без учета сил трения (Рисунок 3-3) определяются величиной массы

и коэффициентом упругости

(3.2)

Отсюда следует, что с увеличением жесткости пружины увеличивается

и собственная частота, а с увеличением массы собственная частота падает.

Такая механическая система имеет одну степень свободы. Если отвести

тело на некоторое расстояние от положения равновесия и отпустить, то пру-

жина заставит тело двигаться. Тело приобретет при этом определенную ки-

нетическую энергию, минует точку равновесия и деформирует пружину в

противоположном направлении. После этого скорость тела начнет умень-

шаться, пока оно не остановится в другой крайней позиции, откуда сжатая

или растянутая пружина опять начнет возвращать тело в положение равнове-

сия. Такой процесс будет повторяться, при этом происходит непрерывное пе-

ретекание энергии от тела (кинетическая энергия) к пружине (потенциальная

энергия) и обратно.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

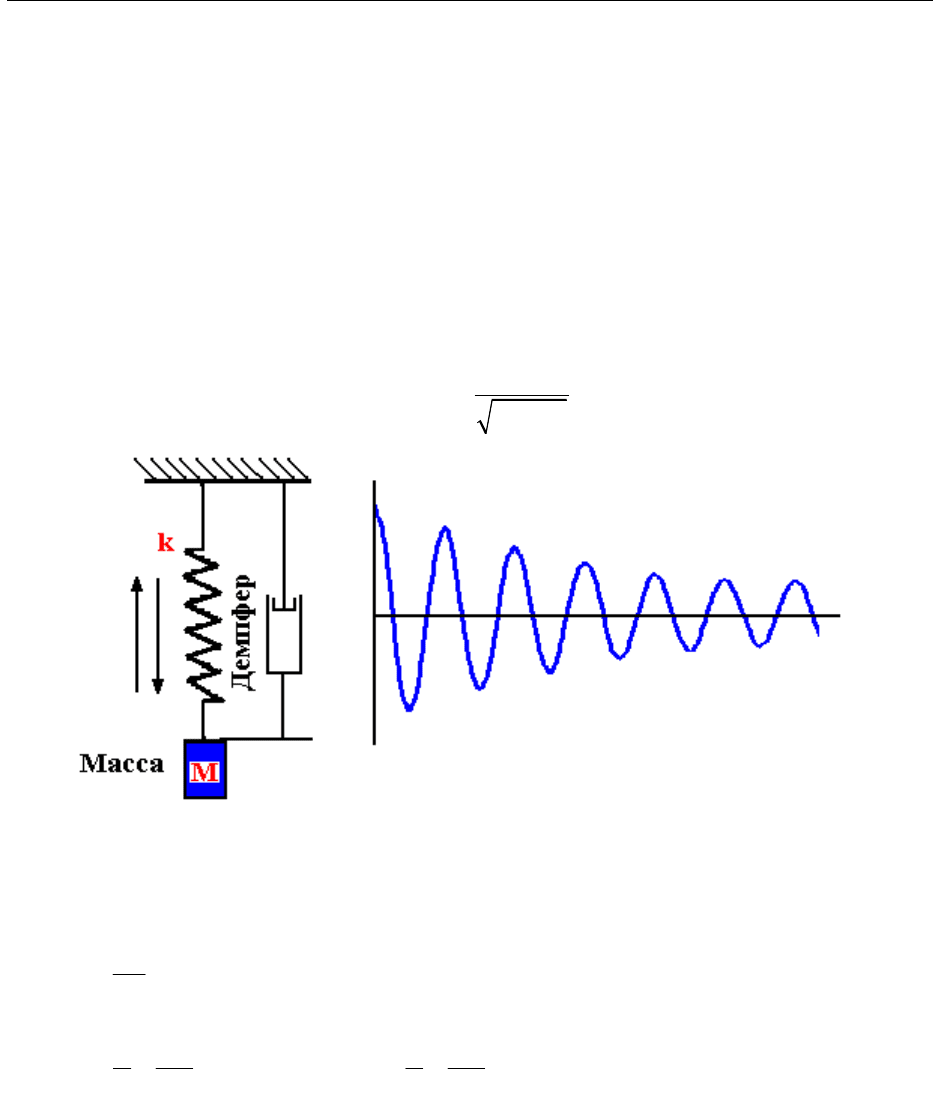
Если бы в системе отсутствовало трение, то эти колебания продолжа-

лись бы непрерывно и бесконечно долго с постоянными амплитудой и часто-

той. Любая реальная механическая система обладает трением (имеет демп-

фирование), которое приводит к постепенному затуханию амплитуды

(Рисунок 3-4) и превращает энергию колебаний в тепло. Движение тела мож-

но описать уравнением:

exp()sin()

xStt=×-×××+

dwj

(3.3)

где

— показатель (коэффициент) затухания.

Такие колебания называются затухающими. Период этих колебаний

тем больше, чем меньше коэффициент затухания:

T =

(3.4)

Рисунок 3-4 – Затухающие колебания системы с демпфером

Для характеристики затухающих колебаний используют следующие

физические величины:

= - коэффициент затухания;

- коэффициент трения;

- декремент колебания;

- логарифмический декремент;

== - затухание;

== - добротность.

Любая механическая конструкция может быть представлена в виде

системы пружин, масс и демпферов, поглощающих энергию. Масса и пружи-

на образуют систему, которая имеет резонанс на характерной для нее собст-

венной частоте. Если подобной системе сообщить энергию (например, толк-

нуть массу или оттянуть пружину), то она начнет колебаться с собственной

частотой, а амплитуда вибрации будет зависеть от мощности источника энер-

гии и от поглощения этой энергии, т.е. демпфирования, присущего самой

системе.

Множество систем пружина-масса-демпфер (то есть простейших ос-

цилляторов), которыми можно моделировать поведение механической конст-

рукции, называют степенями свободы. Энергия вибраций машины распреде-

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

ляется между этими степенями свободы в зависимости от их собственных

частот и демпфирования, а также в зависимости от частоты источника энер-

гии. Поэтому вибрационная энергия никогда не распределена равномерно по

всей машине. Например, в машине с электродвигателем главным источником

вибраций является остаточный дисбаланс ротора двигателя. Это приводит к

заметным уровням вибрации на подшипниках двигателя. Однако если одна

из собственных частот машины близка к оборотной частоте ротора, то ее

вибрации могут быть велики и на довольно большом удалении от двигателя.

Этот факт необходимо учитывать при оценке вибрации машины: точка с

максимальным уровнем вибрации не обяза-тельно располагается рядом с ис-

точником возбуждения. Колебательная энергия может передаваться на боль-

шие расстояния, например, по трубам, и может вызвать большие амплитуды

колебаний при встрече с удаленной конструкцией, собственная частота кото-

рой близка к частоте возбуждения.

Рассмотрим случай, когда груз (Рисунок 3-4) находится в положении

равновесия и на него начинает действовать периодическая внешняя сила

max

cos

. По истечении некоторого времени

(установление колеба-

ний) амплитуда достигнет постоянной величины, которая будет зависеть от

свойств системы и внешней силы:

( )

max

2222

wwdw

(3.5)

где

max

- максимальное значение внешней силы,

- круговая частота изменения этой сипы

Колебания под действием внешних сил называют вынужденными. Если

по истечении времени

сила перестанет действовать, то колебания превра-

щаются в затухающие. При приближении частоты изменения внешних сил к

частоте собственных колебаний в системе наступает резонанс — резкое уве-

личение амплитуды колебаний.

Рассмотренная простейшая колебательная система имела одну степень

свободы (смещение вдоль одной оси координат), сосредоточенные парамет-

ры (пружина обладает только упругостью, a груз - массой), сила трения была

пропорциональна скорости, в случае вынужденных колебаний действовала

одна гармоническая сила. На практике параметры и условия колебаний сис-

тем могут быть и более сложными, однако рассмотренные закономерности

характерны и для этих случаев.

Можно заметить, что в уравнении (3.1) есть четыре переменных – ам-

плитуда (

), частота (

), фаза (

) и время (

). Часто интересует зависи-

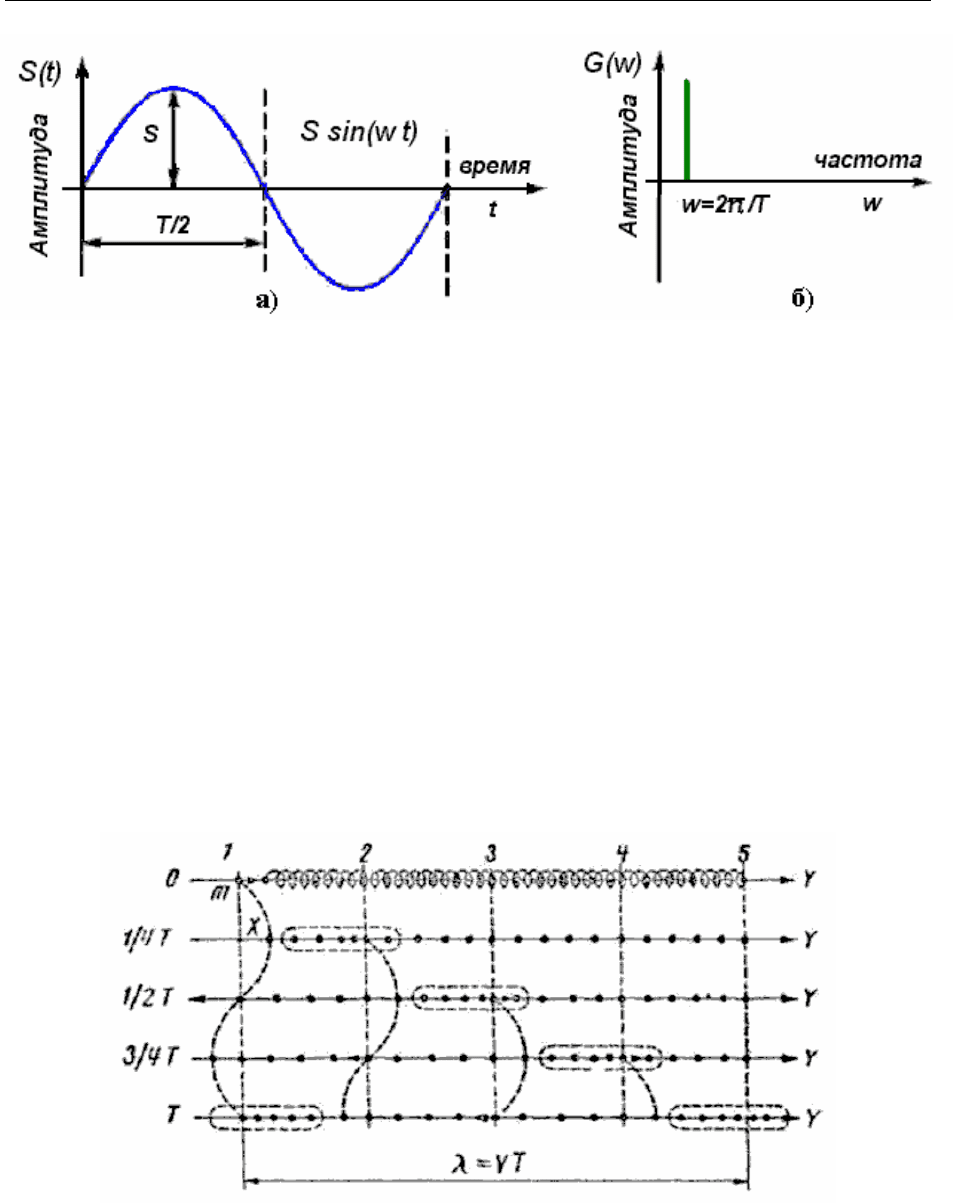
мость амплитуды не только от времени, но и от частоты. Поэтому можно ото-

бражать эту зависимость (3.1) двумя способами: амплитуда как функция

времени (Рисунок 3-5 а)) и амплитуда как функция частоты в определенный

момент времени (Рисунок 3-5 б)). График зависимости амплитуды от частоты

(Рисунок 3-5 б)) называют спектром.

В.Н. Костюков, А.П. Науменко Основы виброакустической диагностики машинного оборудования – 2007 _

Рисунок 3-5 – Амплитуда как функция времени и частоты

3.1.2. Упругие волны

B упругой среде частицы связаны между собой силами. Поэтому про-

стейшей моделью такой среды может служить цепочка грузов с массами и

пружинами, связывающими их между собой (Рисунок 3-6).

В начальный момент все частицы находятся на равных расстояниях

друг от друга. Если теперь привести в движение первую частицу в направле-

нии

на величину

X , то сожмется первая пружина, и сжатие будет распро-

страняться с некоторой скоростью

вдоль всей системы. Этот процесс назы-

вают волной. За время, когда первая масса совершит полный цикл колебания

(

), сжатие распространится на расстояние, называемое длиной волны

. В рассматриваемом случае отдельные частицы смещаются вдоль на-

правления распространения волн, поэтому такая волна называется продоль-

ной в отличие от поперечной, где частицы колеблются перпендикулярно на-

правлению распространения.

Рисунок 3-6 – Модель среды распространения упругих волн

Продольные волны распространяются в жидкостях, газах и твердых те-

лах, поперечные - в основном в твердых телах. Волны одной частоты по

аналогии со световыми называют монохроматическими или гармоническими

Источником волны может служить любое тело, колеблющееся в упругой

среде. В зависимости от формы поверхности этого тела и характера его коле-

баний волна может быть сферической (точечный источник), плоской или ци-

линдрической. Уравнение смещения частиц в плоской гармонической волне