Косчинский С.Л. Основы автоматики и системы автоматического управления
Подождите немного. Документ загружается.

Здесь и далее будем обозначать большими латинскими буквами
векторы и матрицы, а маленькими латинскими буквами – скалярные
переменные.
(Показать переход от (2.1) к (2.2) и обратно.)
Начнем рассмотрение САУ с класса линейных САУ непрерывного
времени.
САУ называется линейной, если она удовлетворяет принципу
суперпозиции.
Т.е. пусть для задающего воздействия U
1
(t), значение
регулируемой переменной х
1
(t), а для U
2
(t) значение регулируемой
переменной х
2
(t). Тогда САУ является линейной, если для
управляющего воздействия на входе САУ вида:
)()(
21
tUtU
значение регулируемой переменной будет иметь
вид:
.,),()()(
21
constconsttxtxtx
Иными словами, САУ является линейной если амплитудные
характеристики всех звеньев САУ (Р, РЭ, ОУ) линейные.
(привести примеры)
ММ линейной САУ в общем виде:
)(...)()()(...)()(
)1(
1
)(
0
)1(
1
)(
0
tUbtUbtUbtxatxatxa
m
mm
n
nn
2.3
Принято приводить ММ к стандартному виду:
.ыебезразмернтыкоэффициеныепередаточн
a
b
K
cвременипостоянные
b
b
T
a
a
T
a
a
Tгде
tUtUTKtxtxTtxT
][
],[,,
)),()(()()()(
2
1
1
1
0
2
2
1
1
2
0
2
0
211
2
0
Или в форме уравнений состояния:
),()(
)(
tUBtXA
dt
tdX
где А и В – квадратная матрица и вектор, Х – вектор
состояния, U – управление.
Хотя в природе в общем случае нет линейных систем, многие
системы содержат слабые нелинейности и первом приближении их
можно рассматривать линейными. Кроме того, теория линейных САУ
является наиболее проработанным (развитым) разделом теории
автоматического управления (ТАУ), что долгие годы побуждало
инженеров искать способы линеаризации реальных систем. Успехи
линейной ТАУ в значительной степени обусловлены использованием
частотных методов (интегральных преобразований), позволяющих
свести анализ САУ от дифференциальных уравнений к
алгебраическим.
Введем понятие оператор дифференцирования
dt
d
p
, тогда ММ
(2.3) примет вид:
)(...)(...
1
10
1
10
tUbpbpbtxapapa
m
mm
n
nn
(2.5)
или
),()()()( tUpRtxpQ
11
где Q(p) – собственный оператор САУ (или оператор объекта
управления),
R(p) – оператор воздействия.
Отношение оператора воздействия к собственному оператору
называется передаточной функцией САУ:
.
)(
)(
)(
pQ
pR
pW
Тогда САУ описывается уравнением:
)()()( tUpWtx
(2.6)
Уравнение (2.6) описывает так называемые вынужденные
колебания в САУ, т.е. колебания от внешнего воздействия U(t).
Операторная форма записи ММ иллюстрирует общий подход к
использованию интегральных преобразований при анализе линейных
САУ. Наиболее мощным средством анализа линейных САУ является
использование интегрального преобразования Лапласа.
)}({)()(
0
txLdtetxsX
st
(прямое преобразование),
j
j
st
sXLdtesX
j
tx
0
0
)}({)(
2
1
)(
1
(обратное преобразование).
Где
js
- комплексная переменная,
X(s) – изображение, x(t) – оригинал.
x(t)=0, при t<0 и возрастает не быстрее экспоненты
ct
eMtx )(
, M=const, C=const. Причем
c
0
.
Основные свойства преобразования Лапласа.
Свойство линейности
)}.({)}({)}()({
2121
txLtxLtxtxL
Дифференцирование оригинала
)0(...)0()0()()}({
)1(21)(
nnnnn
xxsxssXstxL
для
)0()()}({ xsXstxL
(2.7)
Из (2.7) видно различие между операторным представлением ММ
линейной САУ (2.5) и представлением в форме преобразования
Лапласа.
Операторная форма записи описывает только вынужденные
колебания в САУ т.е. колебания, обусловленные внешним
воздействием, а представление ММ линейной САУ в форме
преобразования Лапласа описывает как вынужденные колебания, так
и собственные колебания САУ обусловленные не нулевыми начальными
условиями. Т.е. ММ линейной САУ в форме преобразования Лапласа
имеет вид:
)0()(...)0()()0()()()()(
)1(
321
n
n
xsWxsWxsWsUsWsX
)()(
1
sUsW
- вынужденные колебания
)0()(...)0()()0()(
)1(
32
n
n
xsWxsWxsW
- собственные колебания.
(Пример вынужденных и собственных колебаний.)
Интегрирование оригинала
s
sX
dttxL
t
)(
)(
0
.
12

Теорема запаздывания
)()( sXetxL
s
.
Теорема о свертке
)()()()()()(
212121
sXsXdttxxLtxtxL
.
Теорема о предельных значениях
)()0(
lim
SXsx
s
, если
)(x
существует то
)()(
lim
0
SXsx
s
.
Теорема о разложении
)s(B
)s(A
)s(X
- рациональная дробь, причем
степень полинома числителя меньше степени полинома знаменателя,
то оригиналом x(t) является
st
n
k
)1n(
)1n(
ss
k
e)ss()s(X
ds
d
)!1n(
1
)t(x
k
k
k
k
lim
где S
k
–корни уравнения B(s) =0, n
k
– их кратности, l – число
различных корней.
Если все корни различные, то
ts
k
k
k
e
)s(B
)s(A
)t(x
, где n – степень полинома B(s),
k
ss
k
ds
dB
)s(B
.
Таблица преобразований Лапласа.
)()(
1
sXLtx
)()( txLsX
(t) 1
1(t)
s
1
t
e
s
1
n
t
1
!
n
s
n
tn
et
1
!
n
s
n
t
0
cos
2
0
2
s
s
t
0
sin
2
0
2
0
s
tcose
0
t
2
0
2
s
s
Лекция 3. Частотные и временные характеристики линейных САУ.
13
На предыдущем занятии мы установили, что существуют
различные ММ для задач динамики и статики. А также, что основным
описанием САУ является передаточная функция в форме
преобразования Лапласа
).()()( sUsWsX
Сущность преобразования Лапласа заключается в том, что
любой произвольный сигнал во времени U(t) можно представить в
виде бесконечной суммы комплексных экспонент
tj
e
. Тогда
прохождение этого сигнала через линейную САУ можно представить
как умножение комплексных экспонент в сигнале U(t). При этом
передаточная функция САУ W(s) при замене s на
j
)(
js
, может
рассматриваться как соответствующая зависимость этого
комплексного передаточного коэффициента от частоты.
Функция
)(
jW
, получающаяся при подстановке
js
в
передаточную функцию САУ W(s) называется частотной передаточной
функцией.
)(W
2
)(W
2
)(j
)(W)(W
ImRe)j(W
e)j(WImjRe)j(W
)(
)(
Re
Im
))(arg()(
W
W
arctgjW
Кривая
)(
jW
на комплексной плоскости
)()(
Im,Re
WW
c
называют амплитудно-фазовой частотной характеристикой (АФЧХ).
Причем
)(
jW
- называют амплитудно-частотной характеристикой
(АЧХ), а
)(
j
- называют фазо-частотной характеристикой (ФЧХ).
Частотные характеристики придают наглядность передаточной
функции и служат основой для различных графических методов
синтеза САУ.
Для лучшего понимания физической сущности частотных
характеристик найдём реакцию произвольной линейной САУ на
управляющее воздействие
)tcos(U)t(U
m
.
Представим
)t(U)t(U
2
ee
U)t(U
21
tjtj
m
,
)t(Uj
dt
)t(dU
1
1
,
)t(U)j(
dt
)t(Ud
1
m
)m(
1
)m(
.
Найдём частное решение линейной САУ на управляющее
воздействие
)t(U
1
.
)t(Ub...)j(b)j(b)t(xa...papa
1m
1m
1
m
01n
1n
1
n
0
Будем искать решение в виде
tj
m
e
U
AUAx
2
1111
, где А
1
не
зависит от времени, тогда
14

)(
1
1
10
1
10
1
1
1
1011
1
10
2
)()(
)()(
...
...
)(...)(...
tj
m
j
n
nn
m
mm
m
mm
n
nn
e
U
jWtx
ejWjW
ajaja
bjbjb
A
tUbjbjbtUAajaja
Аналог
ично, для частного решения x
2
(t) получим:
)cos()()()()(
2
)()(
)()(
21
)(
2
2
tUjWtxtxtx
e
U
jWtx
ejWjWA
m
tj
m
j
т.е. при гармоническом воздействии на линейную САУ
вынужденные колебания в САУ также изменяются по гармоническому
закону. При этом отношение амплитуд входных и выходных величин
равно модулю передаточной функции, а сдвиг фаз – аргументу
передаточной функции для данной частоты.
Часто при анализе линейных САУ используютлогарифмические
частотные характеристики:
)(lg20)(
jWL
- ЛАЧХ и
)(
- ЛФЧХ в зависимости от
lg
. Единицей
)(
L
является децибел [дБ], единицей
lg
является
декада (октава).
На практике при построении логарифмических частотных
характеристик используют так называемый асимптотический метод:
1.Определить все сопрягающие частоты
к
т.е. корни полиномов
числителя и знаменателя, взятые с обратным знаком.
2.Преобразуется частотная передаточная функция к виду
n
n
m
m
1j
1j
K)j(W
3.Выполняется построение асимптотических характеристик
отдельных элементов передаточной функции. Т.е. для компонент
1
к
j
4.Суммируем асимптоты. Причем асимптоты числителя со знаком
«+», а асимптоты знаменателя со знаком «-». Что следует из
cbda
cb
da
lglglglglg
и из представления Эйлера комплексного
15
числа
a
b
arctgj
ebajba
22
следует
i
n
i
m
n
n
m
m
)1jarg()1jarg(Karg
1j
1j
Karg
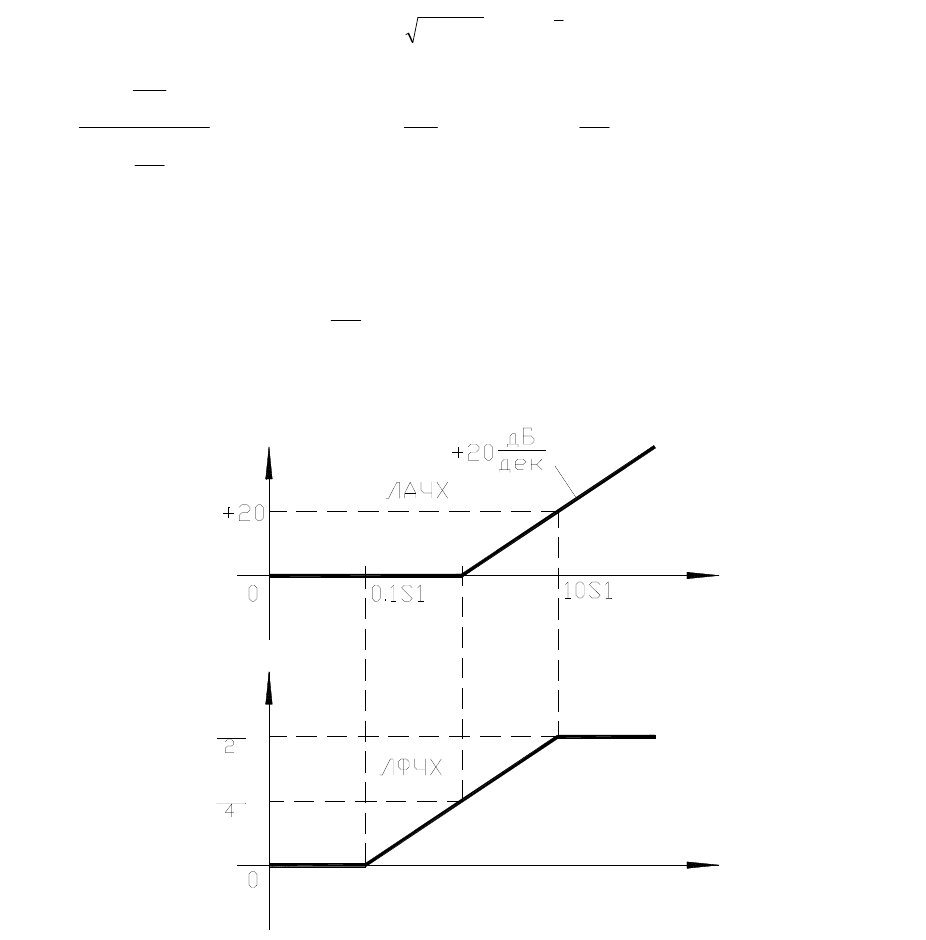
Особенности построения асимптот
Для сомножителя
1
к
j
в знаменателе (числителе)
)j(W
,
асимптота имеет вид:
Рисунок 3.1а. В числителе
16
lg(
(
L(
lg(
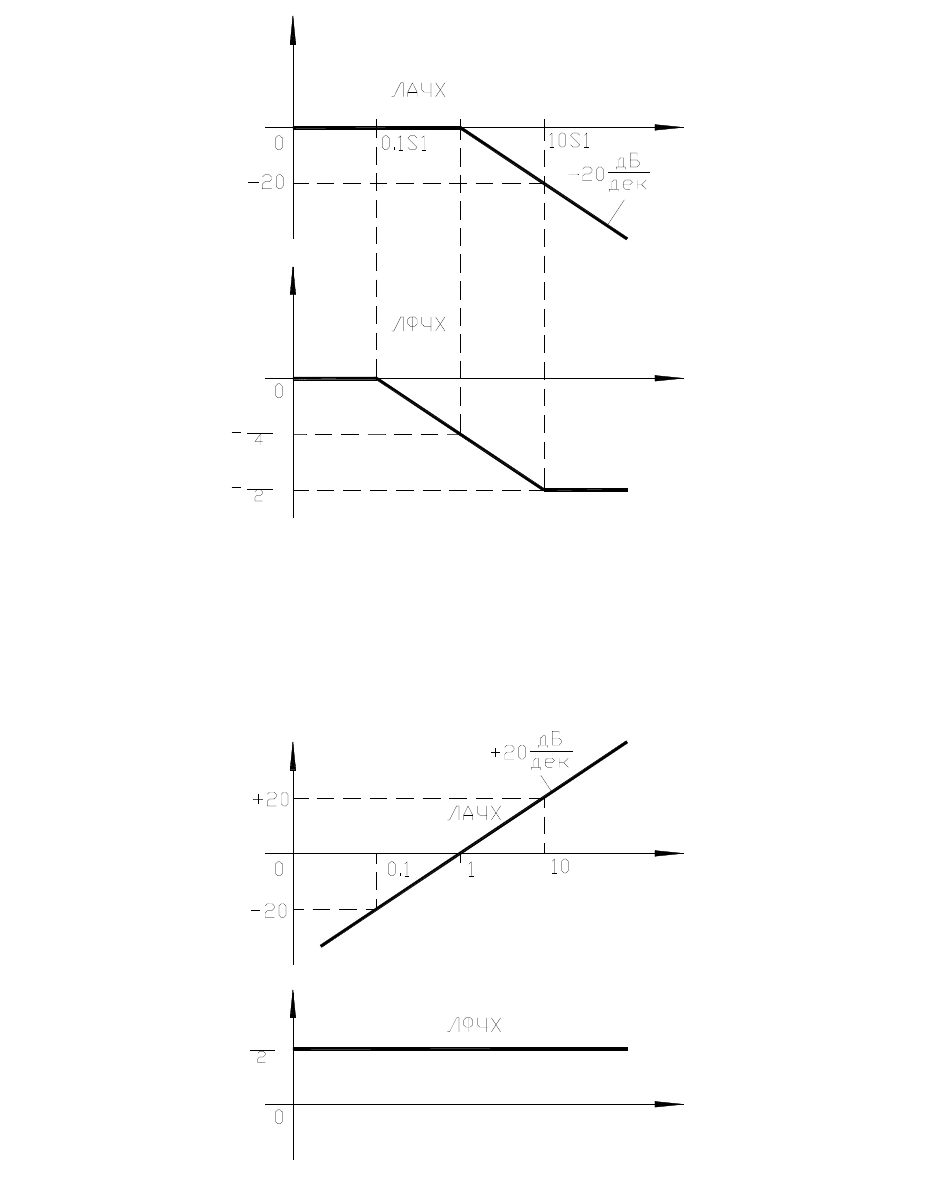
Рисунок 3.1б. В знаменателе
Для сомножителя
j
в знаменателе (числителе) частотной
передаточной функции асимптота имеет вид:
Рисунок 3.1в. В числителе
17
lg(
lg(
(
L(
lg(
lg(
(
L(
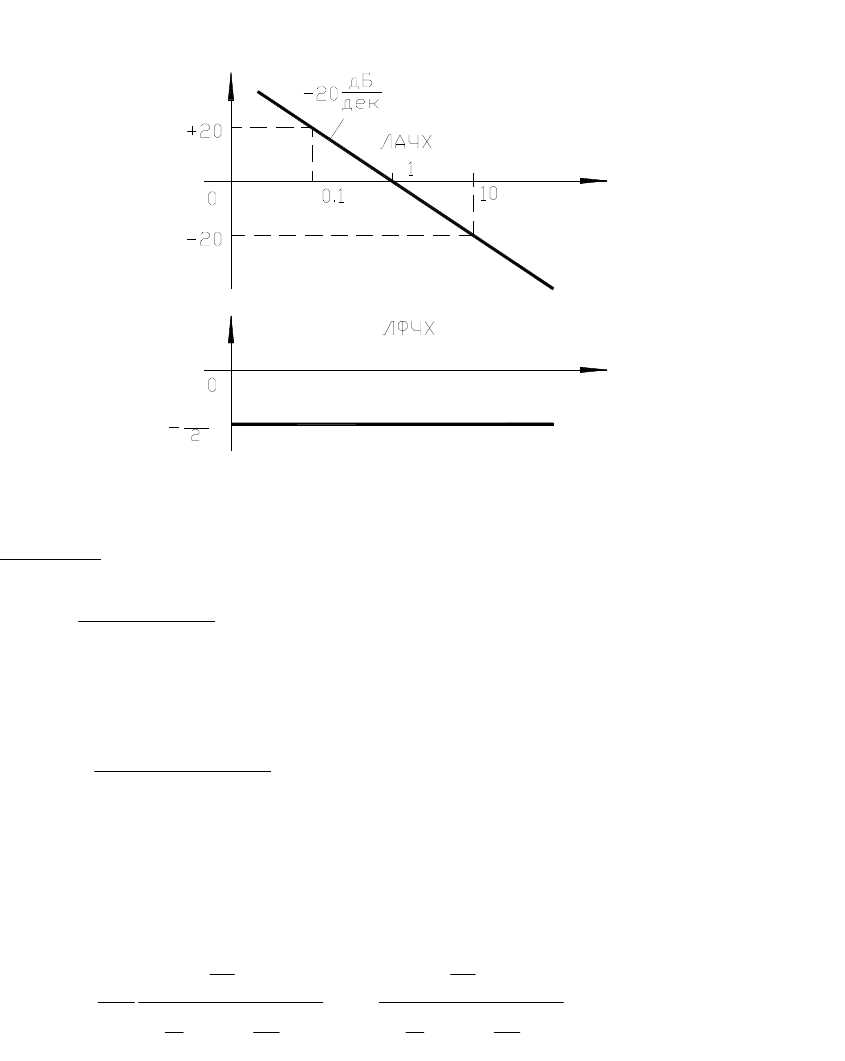
Рисунок 3.1г. В знаменателе
Пример: Построить асимптотическую ЛАЧХ и ЛФЧХ для САУ с
передаточной функцией
100s25s
50s5
)s(W
2
1.Определим сопрягающие частоты
- корни числителя
10s
1
- корни знаменателя
5s
2
20s
3
)20j)(5j(
)10j(5
)j(W
,
тогда сопрягающие частоты:
20,5,10
321
.
2.Преобразуем частотную передаточную функцию к удобному для
построения виду:
)1
20
j)(1
5
j(
)1
10
j(
5.0
)1
20
j)(1
5
j(
)1
10
j(
100
50
)j(W
3.Стоим асимптоты
18
(
L(
lg(
lg(

Рисунок 3.2.
4.Сумируем асимптоты
Рисунок 3.3.
- полюсы частотной характеристики,
- нули частотной характеристики.
Суммарное количество полюсов и нулей равно числу сопрягающих
частот.
19
lg(
lg(
L(
(
lg(
lg(
(
L(

Временные характеристики
Наряду с описанием в частотной области линейные САУ м/б
описаны во временной области. Для подобного описания используют
импульсную переходную функцию и переходнуюхарактеристику.
Импульсной переходной функцией САУ называют реакцию САУ на
единичный
- импульс и обозначают
)(tW
.
,)()(
)0()()(1)(
1
sWLtW
dtttdtt
где W(s) – передаточная функция САУ.
Если в терминах преобразования Лапласа реакция линейной САУ
на управляющее воздействие U(s) имеет вид
),()()( sUsWsX
то во
временной области подобная реакция может быть найдена через
операцию свертки
t
dUtWtx
0
)()()(
.
(привести пример свертки).
Переходной функцией САУ h(t) называется ее реакция на
единичную ступенчатую управляющую функцию 1(t).
Переходная функция м/б выражена через передаточную функцию
САУ:
s
sWLth
1
)()(
1
.
Временные характеристики используют для оценки показателей
качества САУ.
20
