Корнилов И.А. Элементы страховой математики

Подождите немного. Документ загружается.

201

После заключения договора об эксцедентном перестраховании:

;

∫∫

∫∫∫

∫

∞∞

∞∞∞

⋅+⋅−=⋅⋅−−=

=⋅⋅+⋅⋅−⋅⋅=

=>⋅+⋅⋅=

MM0

dyM)f(yyM(X)dxf(x)M)(xM(X)

dxf(x)Mdxf(x)xdxf(x)x

M)Pr(XMdxf(x)xM(Y)

y = x - M; если x > M, то подынтегральная функция > 0; тогда

интеграл

> 0; следовательно: M(Y) < M(X) .

В частности, для

экспоненциального распределения:

M(X)=1/λ, M(Y)=(1-e

-λ⋅M

)/λ .

Учитывая, что D(X) = M(X

) - (M(X))

, получим требуемые

результаты.

11.2. Особенности перестрахования имущества. Пример

различных вариантов договоров о перестраховании

Следуя Штраубу /32/, обозначим:

S - страховая сумма,

X - величина возмещения,

X/S - уровень страховых возмещений,

K - количество случаев за год,

Z - суммарная величина возмещений,

Z - брутто,

•

- перестраховочное,

ZZZ

−

•

- нетто;

P - премия, P =(1 + d)M(Z) - брутто премия за вычетом издержек,

)Zd)M((1P

••

- перестраховочная,

•

−

PPP

- нетто;

d - нагрузка передающей компании,

•

- нагрузка

перестраховщика.

Если нагрузки не равны, то из-за прибыли (или убытках) на

комиссии ожидаемые брутто и нетто прибыльности передающей

компании могут различаться.

квотном договоре с удержанием: 0 < a < 1 имеем:

ZaZ X,aX ⋅=⋅=

эксцедентном договоре передающая компания оставляет себе

одну линию», а перестраховщик берет не более (например) 10 линий, но

мы сначала считаем емкость договора неограниченной, поэтому:

XX =

, при S < m = одна линия,

m/SXX ⋅=

при S > m .

Перестрахование

эксцедента убытка:

202

0X =

•

, при X < r = удержание,

rXX

−

•

, при X > r .

Очевидно:

⋅

−= XXX

,XZ

∑

ZZZ

−

⋅

(K - число брутто возмещений).

Стоп лосс влияет на

•

= 0 , при Z < h × P = точка стоп лосс ,

•

= Z – h × P , иначе.

В /32/ приведен пример, иллюстрирующий ответственность

цедента и перестраховщика (а также их доли в полученных взносах) для

различных договоров. Наши комментарии к примеру должны облегчить

восприятие.

Пример 1.

риск/ставка 0,001 0,002 0,003

A 0,1

B 0,2 страховые

C 0,3 суммы (млн.)

D 2,0

E 10,0

F 20,0

убыток

B 0,15

F 2,55

всего

страховая сумма 0,6 2,0 30,0 32,6

Брутто премия 0,0006 0,004 0,09 0,0946

Объем убытка 0,15 0 2,55 2,7

Примеры вариантов перестрахования перестраховщик

премии убытки

квота 30% 28380 810000

2. эксцедент с максимумом 4 линии сверх 0,1; 0,5; 2,5 (млн.). 55800 1350000

3. факультативно 22500 956250

эксцедент убытка 4 млн. превышающего 1 млн. 24000 1550000

эксцедент убыточности 8 млн. сверх 2 млн. 23215 700000

Комментарии к таблице.

1. Перестраховщик принимает участие в оплате

всех убытков,

поэтому его риск:

2.7 млн. × 0,3 = 0,81 млн., и соответственно, его

премия:

94.6 тыс. × 0,3 = 28,38 тыс.

2. Риск

A меньше границы ответственности перестраховщика

(

0,1млн.), поэтому не учитывается;

203

− по риску B ответственность перестраховщика: 0,2 – 0,1 = 0,1;

− по риску C соответственно: 0,3 – 0,1 = 0,2;

− по D: риск может быть от 0,5 до 4 × 0,5 = 2,0, но не более 2,0 – 0,5 =1,5,

поэтому окончательно до

1,5;

− по E: от 2,5 до 4 × 2,5 = 10,0; но не более 10,0 – 2,5 = 7,5; окончательно

до

7,5;

− по F: риск от 2,5 до 4 × 2.5 = 10,0; но не более 20,0 – 2,5 = 17,5;

окончательно - до

10.

Поэтому в соответствии с риском премия составит:

0,001 × ((0,1 – 0,1) + (0,2 – 0,1) + (0,3 – 0,1)) + 0,002 × (2,0 – 0,5) +

+ 0,003 × ((10,0 – 2,5) + (20,0 –1,0)) = 0,001 × (0,1 + 0,2) + 0,002 ×1,5+

+ 0,003 × (7,5 +10,0) = 0,0003 + 0,003 + 0,0525 = 0,0558 (млн.)

Убытки определяются из доли ответственности перестраховщика в

ущербе: по

B (0,1 из 0,2), по F (10,0 из 20,0), поэтому:

0,1/0,2 × 0,15 + 10,0/20,0 × 2,55 = 1,350 (млн.).

3. Факультативный договор предусматривает перестрахование

только риска

F пропорционально (ответственность перестраховщика

составляет

37,5% от фактического ущерба), поэтому он получает эту

долю премии за риск

(60000 × 0,375 = 22500)

и оплачивает эту долю убытка: (2550000 × 0,375 = 956250).

4. Перестрахованы лишь два

наибольших риска (E и F), причем по

риску

E передано 4 млн. из 10 млн., то есть 4/10 = 40% риска, а по риску

F передано 4 млн. из 20 млн., то есть 4/20 = 20% риска. Поэтому премия

перестраховщика составит:

0,4 × 30 + 0,2 × 60 = 24 тыс.

а выплаты составят:

2,55 – 1,0 = 1,55 млн.

5. Суммарный риск

32,6 млн. Передан риск от 2000001 до

10000000 включительно, то есть 8 млн. Соответственно,

доля премии:

8/32,6 × 94,6 = 23,215 (тыс.);

доля выплаты:

2,7 – 2,0 = 0,7 (млн.).

204

11.3. Анализ целесообразности заключения договора о

перестраховании

Пример 2. Компания имеет 10000 договоров, по которым в

течение года могут быть выплачено: либо частичная компенсация в

е.с.с. с вероятностью

0,002, либо полная компенсация в 10 е.с.с. с

вероятностью

0,0005. (1 е.с.с. равна 100000 ). Проанализировать

положение компании на предмет перестрахования риска /14/.

Решение. Обозначим: Xi – ущерб страховщика в одном договоре,

X= Σ Xi -общий ущерб страховщика во всем портфеле. (Расчеты можно

выполнять как в обычных денежных единицах, так и в е.с.с.). Рисковая

премия равна математическому ожиданию ущерба в одном договоре, т.е.

M(Xi) =1 × 0,002 + 10 × 0,0005 = 0,007 е.с.с. (700 денежных

единиц).

Дисперсия

D(Xi):

M(Xi

) – M(Xi)

= 1 × 0,002 + 100 × 0,0005 – 0,007

= 0,052

(5,2×10

ден.ед.

Среднее квадратическое отклонение:

0,23 (2,3 ×10

ден.ед.).

Тогда для вероятности выживания

0.95 имеем: (1-Ф(t))/2=0.05,

t=1.645, d = 1,645 × 0,23/100 = 0,00375

т.е. нетто – премия:

0,007 + 0,00375 = 0,01075 е.с.с. (1075 ден.ед.).

Соответственно, относительная надбавка:

0,00375/0,007 = 53,6%.

Это объясняется достаточно большой вариацией риска:

0,23/0,007 = 32,6!

Об этом подробно говорится в разделе "

Степень риска".

Для всего

портфеля (из независимости Xi : M(X) =N*M(Xi);

D(X) = N*D(Xi), )

⋅M(Xi)=10000

⋅

0.007=70, N

⋅

D(Xi)=10000

⋅

0.0052=520,

СКО=

520

=22.8, К= CKO/MO=22.8/70=0.326.

Отметим, что суммарный нетто-взнос: 10000 × 0,01075=107,5 е.с.с.

Ожидаемые общие выплаты равны суммарному рисковому взносу

е.с.с. Тогда ожидаемая прибыль:

107,5 – 70 = 37,5 е.с.с. равна суммарной

рисковой надбавке.

Пример 3. Предположим, что страховщик решает перестраховать

большие риски. Т.е. собственное удержание равно

1 е.с.с. (100000

ден.ед.). А перестраховщик устанавливает свою рисковую надбавку в

60%. Проанализировать позиции сторон.

Решение. Разобьем риск страховщика до заключения договора о

перестраховании

X на 2 составляющие: Y – оставленный риск и Z –

переданный риск. Здесь для цедента есть только два значения иска (

Yi):

1 е.с.с. и 0 с вероятностями: (0,002 + 0,0005 = 0,0025) и (1–,0025=0,9975),

205

соотвественно. Следовательно,

индивидуальные среднее значение и

дисперсия равны:

М(Yi) = 1 × 0,0025 = 0,0025

е.с.с. (250 ден.ед.),

D(Yi) = 1

×0,0025 +0

× 0,9975 - 0,0025

= 0,0025 е.с.с. (25 × 10

ден.ед.

СКО = 0,05 е.с.с. (5000 ден.ед.).

Коэффициент вариации:

0,05/0,0025 = 20 существенно

уменьшился, но продолжает оставаться довольно большим.

С позиции

перестраховщика ситуация следующая: Его

индивидуальный иск (

Zi) принимает два значения: 9 е.с.с. (900000

ден.ед.) и

0 с вероятностями: 0,0005 и 0,9995.

Тогда среднее значение равно:

М(Zi) = 9 × 0,0005 = 0,0045 е.с.с.

(

450 ден. ед.), а дисперсия: D(Zi) = 9

× 0,0005 + 0

× 0,9995 -0,0045

0,0405

. Следовательно, для всех договоров, переданных на

перестрахование,

суммарная рисковая премия составит: М(Z) = 10000 ×

0,0045 = 45

е.с.с., а с учетом своей относительной рисковой надбавки

(

60%) общая нетто-премия: 45 × 1,6 = 72 е.с.с..

(Отметим, что в этом примере, где относительная рисковая

надбавка перестраховщика уже известна, вычислять его дисперсию не

надо. Она нужна, скорее, для сравнения с дисперсией цедента после

заключения перестраховочного договора и иллюстрирует процесс

передачи риска.)

Итак, страховщик собрал

10000 × 0,01075 = 107,5 е.с.с. нетто-

взносов (70-РП и 37.5-РН) и из них заплатил перестраховщику

72 е.с.с. У

него осталось 35,5 е.с.с. – одна треть собранных премий (две трети ушли

к перестраховщику!). Ожидаемый доход страховщика:

35,5 – 25 = 10,5

е.с.с. (вместо

37,5 !).

Рассмотрим, как перестрахование отразилось на вероятности

разорения цедента.

До перестрахования эта вероятность равна 5%.

После перестрахования «разорение» означает превышение суммарного

размера требований (к страховщику!), т.е.

Y величины его остатка – 35,5

е.с.с. (выполняем нормирование Y):

(Y > 35,5) = P

((Y – 10000 × 0,0025)/(0,0025 × 0,9975 × 10000)

0,5

> (35,5 – 25)/5)= (1 – Ф(10,5/5))/2 = (1 – Ф(2,1))/2 = (1 – 0,9643)/2 =

1,8%.

Итак, удалось снизить вероятность разорения с 5% до 1,8% за

счет уменьшения ожидаемого дохода в

3,5 раза.

Пример 4. Попробуем с позиции страховщика улучшить его

положение, варьируя размер удержания:

1 < r < 10.

Решение. Индивидуальный иск к основному страховщику Yi

принимает

3 значения: 1 е.с.с., r е.с.с. и 0 с вероятностями: 0,002; 0,0005;

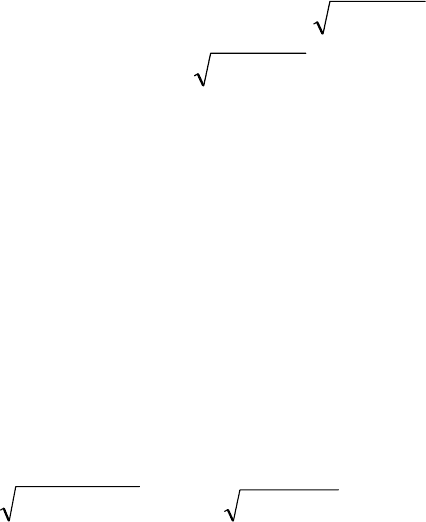
206

0,9975.

Его среднее значение и дисперсия, равны:

M(Yi ) = 1 × 0,002 + r × 0,0005 + 0*0.9975 = 0,0005 × (r + 4);

M(Yi

)=1

*0.002+r

*0.0005+0=(r

+4)*0.0005

D(Yi ) = (r

+4)*0.0005 – 25 × 10

-8

× (r + 4)

= 0,0005 × (r

+ 4).

Иск к перестраховочной компании Zi принимает значения: 0 с

вероятностью

0.9995 и (10-r) с вероятностью 0.0005. Поэтому:

Среднее значение одного иска к перестраховочной компании:

M(Zi ) = 0,007 – 0,0005 × (r + 4) = 0,0005(10 – r)

А дисперсия (аналогично Х):

D(Zi )=M(Zi

)=(10-r)

*0.0005

Плата за перестрахование одного иска (с учетом

θ*) равна:

1,6 × 0,0005(10 – r) = 0,0008 × (10 – r).

Характеристики суммарного иска к страховщику:

N × M(Yi) = 10000 × 0,0005 × (r + 4) = 5(r + 4);

N × D(Yi) = 10000 × 0,0005 × (r

+ 4) = 5(r

+ 4).

Среднее значение и дисперсия суммарного иска к

перестраховщику:

N × M(Zi) = 10000 × 0,0005 × (10 – r) = 5 × (10 – r)

N × D(Zi) = 10000 × 0,0005 × (r

+ 4) = 5 × (r

+ 4)

Общая плата цедента перестраховщику равна:

10000 × 0.0008 × (10 – r) = 8 × (10 – r) = 80 – 8r

Поэтому капитал (ожидаемый доход) цедента после

перестрахования:

107,5 – 8 × (10 – r) = 27,5 + 8r

Разорение цедента наступит, если суммарный иск к нему Y

больше этого значения капитала. Используя нормальную

аппроксимацию, найдем вероятность разорения:

Ф(t)).0,5(1)205r3r)/Ф((7,50,5(1

))205r4))/5(r8r)Ф(((27,50,5(1

−=++−=

=++−+−

Для минимизации вероятности разорения надо максимизировать

аргумент

t функции Ф. Рассмотрим: t

= (7,5 + 3r)

/(5r

+ 20) и найдем

производную от него. Она равна:

d(t

)/dr = (2(7.5 + 3r) × 3 × (5r

+ 20) – (7.5 + 3r)

× (10r))/(5r

+20)

(30r

+ 120 – (7.5 + 3r) × 10r) × (7.5 + 3r)/(5r

+ 20)

(30r

+ 120 – 75r – 30r

) × (7.5 + 3r)/(5r

+ 20)

(120 – 75r) × (7.5 + 3r)/(5r

+ 20)

2*(7.5 + 3r) × (12 – 7.5r)/(5(r

+ 4)

);

d(t

)/dr =2 × (7,5 + 3r) × (12 – 7,5r)/ (5(r

+ 4))

Приравняв нулю и учитывая, что r > 0, получим: r = 12/7,5 = 1,6

е.с.с. (в абсолютных значениях:

160000), тогда:

2,1512,3/5,72012,812,3/201,651,6)/3(7,5t

==+=+⋅⋅+=

207

Ф(2,15) = 0,9684; (1 – Ф(t))/2 = 0,0158 = 1,58%.

А средний доход компании: 7,5 + 3 × 1,6 = 12,3 е.с.с. (1230000).

Таким образом, если изменить предел удержания с

1 е.с.с. на 1,6 е.с.с.,

то

вероятность разорения уменьшится, а ожидаемый доход возрастет.

В качестве упражнения рекомендуется рассмотреть различные

значения

r, например, 1,3; 2,0; 2,5; и исследовать влияние r на

вероятность разорения (или, наоборот, выживания), ожидаемую

прибыль, степень риска цедента. Можно также проанализировать

показатели перестраховщика.

Замечание. В этом примере условие сформулировано корректно:

а) полная компенсация существенно выше частичной,

б) соответствующая вероятность, наоборот, существенно ниже,

в) у перестраховщика относительная рисковая надбавка выше, чем

у цедента, но

соизмерима с ней.

Поэтому проблем не возникает. Функция зависимости вероятности

разорения цедента от его уровня собственного удержания – строго

выпукла, имеет глобальный минимум, который можно найти, приравняв

нулю первую производную. При выполнении перечисленных условий

оптимальное решение находится

внутри интервала, указывающего min

и max возможного уровня удержания.

При выполнении студентами домашнего задания по данному

примеру выяснилось, что иная ситуация возникает, если задача

сформулирована

некорректно. Например, относительная рисковая

надбавка у перестраховщика в несколько раз выше, чем у цедента. Тогда

глобальный минимум находится

вне допустимого интервала. Это

означает, что плата за перестрахование – слишком велика. Поэтому для

цедента имеет смысл перестраховать только

очень большие риски,

которых у него нет. (Отсутствует приемлемое решение.)

На отрезке, задающем область допустимых решений, первая

производная – отрицательна, т.е. чем больше уровень собственного

удержания, тем лучше для цедента. Таким образом получено

математическое объяснение мотивов поведения на страховом рынке в

данной ситуации. Видно, что перестраховщик не может решить всех

своих проблем за счет своей рисковой надбавки.

Пример 5

. Компания имеет N = 20000 договоров на 1 год.

Вероятность случая у всех одинакова и равна

0,01, тогда страховая

сумма выплачивается полностью, иначе выплаты нет. Но страховые

суммы различны:

=10000, S

=100000; N

=5000, S

=200000; N

=4000,

=500000; N

=1000, S

=1000000. Относительная рисковая (страховая)

надбавка установлена компанией (для всех одинакова)

15%.

Исследовать целесообразность перестрахования превышения потерь при

пределе удержания

500000, если у перестраховщика относительная

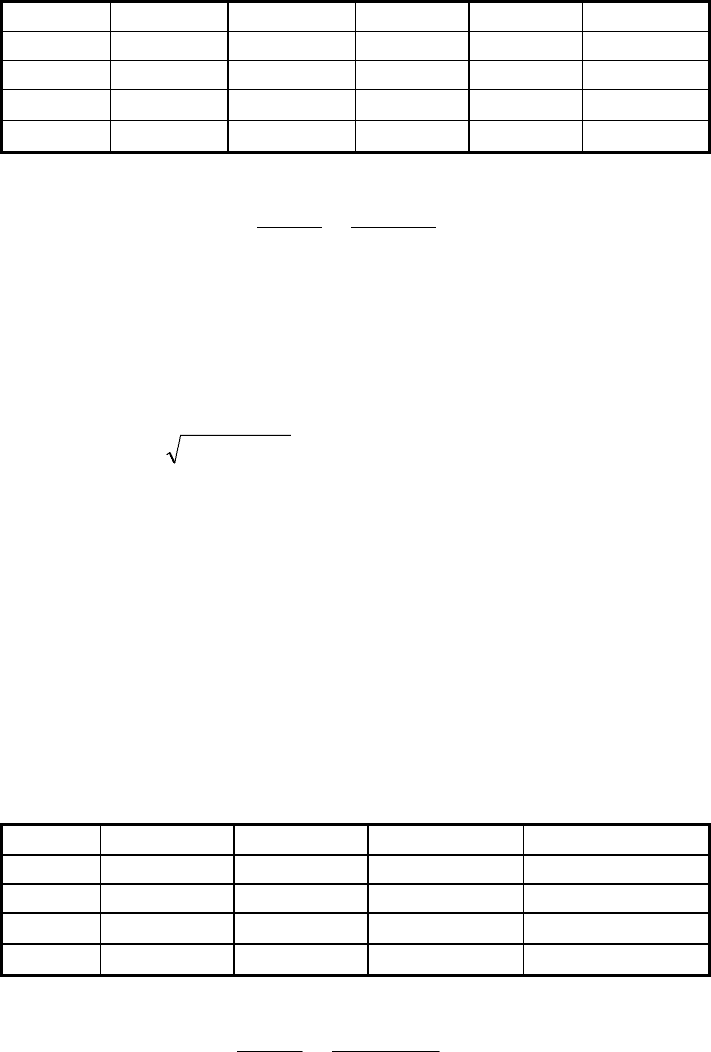
208

надбавка

20% /13/.

Решение.

5-1. Оценим вероятность разорения и ожидаемый доход без

перестрахования. Сгруппируем иски по величине

S. Т.к. M(Xi) = Sp,

D(Xi) = S

pq, то:

M(X) = NSp; D(X) = D(NSp) = NpqS

. (= NpS ×qS). Составим таблицу.

Группа 1 2 3 4 Всего

N 10000 5000 4000 1000 20000

S 100000 200000 500000 1000000

NSp 10

2 ×10

5 ×10

D(NSp)

99 ×10

198 ×10

990 ×10

2277×10

9.6%

105

1048

МО

СКО

⋅

Итак, страховщик в виде нетто-премий собрал:

(1 + 0,15) × (5 ×10

) = 5,75 ×10

; (57.5 е.с.с.),

а ожидаемый доход (разность между собранными нетто-премиями и

ожидаемыми выплатами):

5,75 ×10

- 5 ×10

= 0,75 ×10

= 7,5 млн. (0.75 е.с.с.) Тогда

t = (0,75 ×10

102277 × = 75/48 = 1,57,

следовательно, вероятность разорения равна:

(1 – Ф(1,57))/2 = (1 – 0,8836)/2 = 0,06 = 6%.

5-2

. Теперь рассмотрим договор перестрахования с пределом

удержания

500000 (0.5 е.с.с.). Это означает, что по договорам последней

группы страховщик платит только

500000, столько же, сколько и в

третьей, поэтому эти две группы можно объединить, и тогда получим.

M(X)=NSp, D(X)=NSp*Sq.

Строится аналогичная таблица:

Группа 1 2 3 всего

N 10000 5000 5000 20000

S 100000 200000 500000

NSp 10

2,5 ×10

4,5 ×10

D(NSp)

99 ×10

198 ×10

1237,5 ×10

1534,5 ×10

8.72%

1045

1039.2

МО

СКО

⋅

Итак, средний иск к цеденту уменьшился на 10% (с 50 млн. до 45

млн.), а дисперсия уменьшилась в

1,5 раза (с 2277 до 1534,5), при этом

коэффициент вариации уменьшился с

9,6% до 8,7%.

Средний суммарный иск к перестраховочной компании

5 млн.

209

Плата за него составит

1,2 × 5 = 6 млн. Поэтому капитал передающей

компании уменьшится на эти

6 млн. (с 57,5 до 51,5 млн.). А ожидаемый

доход передающей компании составит

51,5 – 45 = 6,5 млн. (уменьшился

на

1 млн. по сравнению с предыдущим вариантом).

Вероятность разорения после перестрахования равна:

0,5(1-Ф(t)),

66,15,1534/60105,1534/10)455,51(

106

==⋅⋅−=t

P = 0,5(1 – Ф(1,66)) = (1 – 0,9031)/2 = 0,05 = 5%.

Итак, перестрахование уменьшило вероятность разорения с 6% до

5% за счет уменьшения ожидаемого дохода с 7,5 до 6,5 млн.

Дополнение к данному примеру. В примере рассмотрены два

варианта: без перестрахования и с перестрахованием при уровне

удержания

500000. Разумеется, можно найти оптимальный уровень

удержания. При этом отдельно анализируется интервал (

0,2 млн., 0,5

млн.) и (

0,5 млн., 1 млн.). Дело в том, что в этих двух интервалах

различен передаваемый риск, а, следовательно, и плата за него, и

вероятность разорения, и ожидаемый доход страховщика. Поэтому

придется оптимизировать

различные функции.

Конечно, необходимо использовать не только первую

производную, но и вторую, знак которой определяет min, max. Однако,

если известен заранее характер оптимума, можно обойтись без второй

производной.

Итак, при

кусочной аппроксимации возникают два локальных

оптимума, из которых надо выбрать

глобальный. Это исследование

целесообразно выполнить в качестве самостоятельной подготовки.

Далее,

с точки зрения страховщика, ситуация выглядит

следующим образом. Он знает характеристики своего портфеля и

условия договора с перестраховщиком. Предположим, что он пришел к

выводу о достаточности суммарной рисковой надбавки

7,5 млн. (или

ожидаемой прибыли без перестрахования) для оплаты перестрахования

и получении некоторой прибыли. Теперь он должен вернуться к анализу

своего портфеля, чтобы решить,

как ему распределить суммарную

надбавку между субпортфелями. (Внутри каждого субпортфеля все

полисы одинаковы, поэтому и надбавки будут равными!).

Следовательно, возникает вопрос о «

справедливом» распределении

этой суммарной надбавки. Напомним, что в первом варианте

предполагалось, что надбавка пропорциональна рисковой премии (или,

что эквивалентно, математическому ожиданию риска). Однако, ситуация

в разных субпортфелях – различна: и из-за разных страховых сумм, и по

причине различных объемов субпортфелей.

Пример 6.

Проанализировать различные варианты формирования

рисковой надбавки по данным предыдущего примера.

Решение. Нетрудно убедиться, что надбавка в 15% обеспечивает

210

разную надежность в каждом субпортфеле. Рассчитаем СКО, степень

риска и вероятность разорения для каждого субпортфеля (

15% = tσ/M).

t=0.15/K; e=(1- Ф(t))/2.

9,95 ×10

14,07 ×10

31,46 ×10

K=σ/M

0,0995 0,1407 0,1573 0,3146

T 1,51 1,07 0,95 0,48

Pr 0,065 0,142 0,171 0,319

Итак, при одинаковой относительной рисковой надбавке

15%

вероятности разорения существенно различны: от 6,5% (меньше, чем во

всем портфеле!) до

30,9% (вдвое больше, чем во всем портфеле!). Таким

образом, благополучие в

4-м субпортфеле обеспечивается за счет

взносов страхователей из

1-го субпортфеля (а также, частично, из 2-го и

3-го).

Очевидно, такая ситуация устраивает клиентов из

4-й группы, но

совершенно не устраивает представителей

1-й группы. (И, в какой-то

мере, клиентов из

2-й и 3-й групп). Важно, что 1-й субпортфель может

вполне обойтись без остальных.

2-й и 3-й могут объединиться (создать

коалицию!) для повышения устойчивости всего портфеля. И они будут

приветствовать объединение с

1-м субпортфелем, если он согласится на

такое объединение. Но они совсем не заинтересованы в объединении с

4-м!

Ясно, что если страховщик не изменит

правила формирования

взносов

в пользу трех первых групп, они выйдут из общего портфеля.

Хотя могут создать новый портфель (коалицию), где ситуация будет для

них более привлекательна.

Клиенты из

4-го портфеля тоже все это понимают, как и то, что

только они заинтересованы в объединении

4-х субпортфелей. Но тогда

они должны согласиться на изменение «правил игры» в пользу своих

партнеров. Это означает, что надбавка в

4-м субпортфеле должна

существенно возрасти, чтобы снизить взносы в 3-х других группах, и

тем самым удержать их от выхода из общего портфеля или создания

коалиции внутри него!

Страховщик, понимая всю эту ситуацию, решает изменить

правило формирования надбавки. Но это может быть сделано на основе

различных принципов. Рассмотрим их поочередно.

Страховщик может назначить рисковую надбавку, исходя из

равенства вероятностей разорения для каждого субпортфеля. При этом

суммарная рисковая надбавка должна приблизительно составлять

7,5

млн. Понятно, что эта задача может быть решена итерационно. Мы

будем постепенно увеличивать вероятность разорения. На основании ее

найдем

t и соответственно, абсолютную и относительную надбавки.

Итак, вероятность разорения увеличим с

0,06 (в рассмотренном

примере) до

0,1. Тогда t = 1,28,