Корнилов И.А. Элементы страховой математики

Подождите немного. Документ загружается.

211

iiiiiii

N12,74/N/991,28

N/q/ptp)/(σpq/Nσt/Mdθ

=⋅=

=⋅=⋅⋅⋅==

= 0,1274 = 13%, θ

= 18%, θ

= 20%, θ

= 40,3%.

Отметим, что для четвертой группы надбавка слишком велика.

Найдем собранные с каждой группы суммы (в млн.):

10 ×1,13 = 11,3; 10 × 1,18 = 11,8; 20 ×1,20 = 24.0; 10 ×1,40 = 14,0.

Всего: 11,3 + 11,8 + 24,0 + 14,0 = 61,1 > 57,5. Это позволяет

снизить надежность в каждом субпортфеле.

Пусть вероятность разорения

0,12. Тогда t = 1,175, относительные

надбавки:

0,1169; 0,1653; 0,1848; 0,3697.

Собрано:

11,169 + 11,653 + 23,696 + 13,697 = 60,2 > 57,5.

Продолжаем процесс.

ε = 0,15; t = 1,037,

: 0,1032; 0,1459; 0,1632; 0,3264.

Собрано: 11,032 + 11,459 + 23,264 + 13,264 = 59.

Наконец:

ε = 0,18; t = 0,915,

: 0,091; 0,129; 0,144; 0,288.

Собрано: 10,91 + 11,29 + 22,88 + 12,88 = 57,96 ≅ 57,5.

На этом можно и остановиться, а можно рассмотреть ε = 0,19, или

0,185.

Другой подход основан на том, что сумма 7,5 млн. распределяется

пропорционально СКО каждой группы,

9,95:14,07:31,46:31,46 или 0,32:0,45:1:1.

Это означает, что группы должны внести (суммарные

абсолютные) рисковые надбавки в размере

0,87; 1,22; 2.71; 2,71. (млн.)

Тогда относительные надбавки составят:

8,7%, 12,2%, 13,6%, 27,1%.

Соответственно,

t: 0,874; 0,867; 0,864; 0,861.

Они практически одинаковы и соответствуют вероятностям

разорения

0,19 по каждому субпортфелю. Результат очень близок к

полученному на основе одинаковых вероятностей разорения.

(В качестве упражнения предлагается объяснить этот эффект).

Наконец, можно ориентироваться не на СКО, а

на дисперсии,

тогда пропорция:

99:198:990:990 или 1:2:10:10. Следовательно, 7,5

млн. распределятся так:

0,326:0,652:32,6:32,6. Соответственно,

относительные надбавки равны:

3,26%; 6,52%; 16,3%; 32,6%. Тогда:

t: 0.328, 0.463, 1.036, 1.036. ε

: 0.37, 0.32, 0.15, 0.15.

Здесь страховщик беспокоится, в основном, о

больших рисках,

игнорируя ухудшение ситуации в субпортфелях с малыми рисками.

Если сравнить все рассмотренные варианты, то наиболее

212

предпочтительно выглядят почти совпадающие варианты, основанные

на равенстве вероятностей разорения или при надбавке,

пропорциональной СКО.

Однако, видно, что проблема существует, решение ее –

неоднозначно, и необходимо ориентироваться на взвешенную формулу.

Нахождение весовых коэффициентов представляет самостоятельную

нетривиальную проблему.

Интересно отметить, что надбавка в

4-й группе около 30% (у

страховщика), а у перестраховщика

20%. Ранее отмечалось, что по

одному и тому же риску надбавка перестраховщика всегда выше.

Возможно, что перестраховщик установил надбавку

20% для всего

портфеля (другой договор - облигаторный!), а при принятии только

больших рисков (факультативный!) он свою надбавку несколько

повысит. Но, с другой стороны, портфель перестраховщика состоит не

только из

4-го субпортфеля. Ему аналогичные риски принесли и другие

цеденты. Объем его портфеля велик, поэтому относительная надбавка

может и не возрасти.

Таким образом, показано, что в имущественном страховании роль

перестрахования имеет свою специфику. Особенно это относится к

крупным рискам. Очевидно, что особенности страхового портфеля

существенно влияют на выбор перестраховочной программы и плату за

перестрахование.

213

12. Концептуальные проблемы перестрахования (и некоторые

смежные вопросы)

12.1.

Проблема определения размера удержания

Сложность проблемы определяется влиянием на выбор решения

целого ряда факторов, таких, как: платежеспособность, емкость,

финансовое состояние, обслуживание, взаимность, выравнивание нетто

результата. На практике ситуация усложняется тем, что стороны

интересует не отдельное, а оптимальная комплексная программа

страхования или перестрахования.

Отметим, что в отличие, например, от страхования

ответственности, где страховая сумма и уровень страховых возмещений

не требуются или даже не определены, в страховании собственности эти

величины играют решающую роль.

Интуитивно ясно, что с ростом капитала необходимость в

перестраховании уменьшается. Аналогично, этому способствует

увеличение вероятности разорения (готовность к риску) и уменьшение

флуктуаций (колебаний, разброса) брутто-итога.

В кн. Штрауба /32/ выведены некоторые рекомендации для

определения уровня удержания в наиболее распространенных

договорах.

В общем виде удержание пропорционально брутто нагрузке

премии и обратно пропорционально величине

q, характеризующей

потребность в перестраховочной защите. (

a = d/q). Для конкретных

договоров это общее правило принимает вид.

1. Для квотного договора:

(

)

()

lnw

dU ⋅













−

⋅⋅

где: U - резерв, w - допустимая вероятность разорения.

2. В эксцедентном договоре подбирается (итерационно) уровень

удержания, чтобы выполнилось условие:

«отношение средних страховых сумм (нетто к брутто) = a».

3. В договоре эксцедента убытка на основе статистики по

отдельным cтраховым возмещениям (для соответствующего приоритета)

аналогично п.2 обеспечивается выполнение условия:

«отношение средних страховых возмещений (нетто к брутто)

a ».

214

4. В договоре эксцедента убыточности аналогично:

«отношение средних суммарных страховых возмещений (н/б) = a».

Кроме решения абсолютной задачи для однородного субпортфеля

необходимо решать относительную задачу для всего неоднородного

портфеля. Интерес представляет зависимость удержания от категории

риска.

Замечание. Полученное выше правило для определения

удержания:

«удержание = капитал

готовность к риску

прибыльность

несбалансированность»

показывает лишь качественное решение задачи.

Более точное

количественное решение получается по формуле:

)/V(Z))Z()/M(Z))/(VY(M(lnw)0,5(V(Z)M(Z)/U

=⋅−⋅⋅

Левая часть характеризует потребность в перестраховочной

защите. Три сомножителя характеризуют ситуацию

до перестрахования

(брутто портфель):

− финансовая слабость: M(Z)/U,

− несбалансированность брутто портфеля: V(Z) = Var(Z)/(M(Z))

− неприятие коммерческого риска: -0,5 × ln w.

Для определения потребности в перестраховании перемножаются:

слабость, несбалансированность и неприятие риска.

В правой части - нетто ситуация (

после заключения договора).

Здесь рассматривается отношение (польза/стоимость)

перестраховочной программы. При удорожании перестрахования

числитель уменьшается, а с ростом эффективности перестрахования

уменьшается знаменатель.

Различие правил для разных договоров свидетельствует о

значительно большей специфике этой задачи по сравнению с задачей

определения тарифов.

12.2. Проблема резервов

Этот вопрос является одним из наиболее сложных и в то же время

важных. В страховании существует много различных видов резервов.

Резервы премий, резервы возмещений, чрезвычайные резервы, резервы

колебания валюты и целый ряд других резервов, каждый из которых

имеет свое назначение.

Резервы премий (незаработанные премии) возникают, если

договор заключен в июле на один год и премия внесена единовременно

(всю первую половину следующего года компания несет

215

ответственность, не получая никаких взносов).

В перестраховании (например, от несчастного случая) резервы

возмещений недостаточны, их приходится увеличивать.

Технические резервы состоят из резервов премий и резервов

возмещений. Они превышают суммарные годовые нетто поступления

приблизительно вдвое. Эти деньги принадлежат не компании, а

клиентам.

Компании необходим резерв случайных рисков для сглаживания

колебаний на рынке.

Особое внимание уделяется капиталам риска или требованиям

платежеспособности - амортизаторам флуктуаций годового результата.

К чрезвычайному фонду предъявляются требования, чтобы он мог

выдержать убытки, которые нанесет компании событие, происходящее

раз в

100 лет.

Естественно, методы расчета существенно зависят от целей

создания резерва и случайных процессов, связанных с этим резервом.

Очевидно, что с одной стороны, проблема резервов является

самостоятельной, но с другой стороны, она тесно связана со всеми

остальными актуарными проблемами, и в первую очередь, с

перестрахованием.

Как отмечено ранее, на практике актуарные задачи решаются в

комплексе, и в большинстве случаев возникает многоцелевая задача,

которую приходится решать итерационно до получения решения,

приемлемого со всех точек зрения.

12.3. Исследование позиции цедента при перестраховании

Смысл страхования для клиента – предотвращение финансовых

потерь, связанных с неопределенностью наступления случайных

событий. Клиент имел некоторый риск, способный привести к

случайным потерям

X, (или не привести). Страховой договор избавляет

клиента (страхователя) от этого случайного риска за неслучайную плату

(1+θ)M(X). Но этот риск не исчез, его принял на себя страховщик.

Имея большой портфель договоров, страховщик обеспечивает

малую вероятность своего разорения. Но возможны очень большие иски,

которые могут привести его к разорению. Т.е. возникает опасность

финансовых потерь из-за неопределенности предъявления очень

больших исков.

Поэтому страховая компания сама стремится застраховать

свой

риск у другого страховщика. Заключается

перестраховочный договор

между

передающей компанией (цедентом) и перестраховочной

компанией.

Перестраховочный договор может охватывать как чрезмерно

большие индивидуальные иски, так и суммарный иск за определенный

период (год). С математических позиций некоторые виды страхования

216

довольно близки к перестрахованию (при наличии существенных

экономических и юридических отличий). Например,

сострахование –

договор нескольких страховщиков с одним клиентом, или

групповое

страхование

– договор работодателя со страховщиком о страховании

работников предприятия.

Договоры перестрахования классифицируются по виду разделения

ответственности между цедентом и перестраховщиком.

Если согласно договору цедент оплачивает долю «a» от каждого

иска (

предел или доля удержания), а остальную долю платит

перестраховщик, то имеет место

пропорциональное перестрахование.

Если цедент оплачивает

индивидуальные иски до предела

удержания r

, а все сверх этого значения оплачивает перестраховщик, то

имеет место перестрахование

превышения потерь или эксцедентное

перестрахование. Если это правило применяется к

общему иску за

некоторый период, то имеет место перестрахование,

останавливащее

потери

, или перестрахование на базе эксцедента убыточности. Здесь r

называется

вычитаемой франшизой.

Перестраховочные договора задаются функцией

h(x),

указывающей сумму выплат перестраховщика при иске

x. Плата за

перестрахование определяется по тем же принципам, что и в обычном

страховании:

(1+θ*)M(h(x)). При рассмотрении перестраховочного

договора с позиции цедента считается, что рисковая надбавка

перестраховщика

θ* – фиксирована. Поэтому выбирается договор

перестрахования и оптимизируется числовой параметр.

Ранее изложена

модель индивидуального риска, предназначенная

для расчета вероятности разорения, основанная на следующих

упрощающих предположениях:

− анализируется фиксированный относительно короткий

промежуток времени (год), что позволяет пренебречь инфляцией и не

учитывать доход от инвестирования;

− число договоров фиксировано и неслучайно;

− взнос – единовременный в начале периода;

− для каждого отдельного договора известны статистические

свойства связанного с ним индивидуального иска.

В этой модели определяется суммарный иск к страховщику. Если

он больше резерва, компания не может выполнить свои обязательства и

разоряется. Поэтому вероятность разорения – это дополнительная

функция распределения величины суммарного иска. Отметим, что

резерв может и увеличиться за счет ожидаемого дохода (разности между

собранными нетто-премиями и математическим ожиданием выплат).

При

пропорциональном перестраховании уменьшается суммарный

иск к цеденту (

aS вместо S) и его капитал: U+(1+θ)M(S) (на

(1+θ*)(1-a)M(S)). Поэтому после заключения договора резерв цедента

станет равным:

U + (θ - θ* + (1 + θ*)a)M(S).

217

Цедент разоряется, если:

aS > U + (θ - θ* + (1 + θ*)a)M(S). Т.е.

S > (1 + θ* + (U/M(S) + θ - θ*)/a).

Исследуем множитель при «a». Если θ*<θ + U/M(S), то при

пределе удержания от

1 (отсутствие перестрахования) до 0 (полное

перестрахование) вероятность разорения цедента убывает от начального

значения

P(S > (1 + θ + U/M(S))M(S)) до 0. При этом ожидаемый доход

уменьшается до:

(1 + θ)M(S) - (1 + θ*)(1 - a)M(S) - aM(S) = (θ - θ* + aθ*)M(S)

Поскольку на практике θ* >θ, то при полном перестраховании

доход отрицателен, т.е. имеет место убыток

(θ* - θ)M(S). Поэтому

параметр «

а» не может быть меньше (θ* - θ)/θ* = 1 - θ/θ*, когда

ожидаемый доход равен

Следовательно, при

θ* < θ + U/M(S) пропорциональное

перестрахование позволяет снизить вероятность разорения за счет

уменьшения ожидаемого дохода. Но при обратном знаке неравенства

уменьшение предела удержания приводит к возрастанию вероятности

разорения, поэтому подобный договор нецелесообразен. Если имеет

место

равенство, то вероятность разорения не зависит от предела

удержания

. Но ожидаемый доход уменьшается с уменьшением предела

удержания, поэтому и здесь перестрахование нецелесообразно.

Проанализируем

перестрахование превышения потерь.

Смысл этого договора в том, что иск

Х разбивается на две

составляющие:

(r)

=min(X,r) – к цеденту, max(X-r,0) – к

перестраховщику. Предполагается независимость и одинаковые

распределения индивидуальных рисков, и соответственно, исков

Собрано взносов:

N(1 + θ)П0, где П0 = M(X).

Плата за перестрахование:

N(1 + θ*)(M(X) - M(X

(r)

)).

Разность – это ожидаемый доход цедента после перестрахования.

Разорение наступает, если суммарный иск к цеденту превышает

этот «скорректированный» ожидаемый доход.

S > N(θ - θ*)M(X) + N(1 + θ*)M(X

(r)

)

Или:

(r)

– NM(X

(r)

) > N(θ - θ*)M(X) + Nθ* M(X

(r)

Теперь при большом N можно использовать нормальную

аппроксимацию (делим обе части неравенства на

()

(r)

XND

). Если

обозначить дробь в правой части неравенства через

t, то вероятность

выполнения неравенства:

(1 - Ф(t))/2. Для минимизации этой

вероятности надо максимизировать t. Экстремум находится

приравниванием к

0 первой производной. (Заметим, что можно искать и

экстремум

). Конечно, в общем случае надо исследовать и вторую

производную, а затем из всех локальных максимумов выбрать

глобальный, но в некоторых частных случаях процесс упрощается.

218

В рассмотренных задачах исследовалась вероятность разорения в

зависимости от условий перестрахования без учета влияния резерва. В

других задачах, наоборот, исследовалось влияние величины резерва на

вероятность разорения, но без учета перестрахования. Реальный

страховщик, разумеется, решает комплексную задачу, пытаясь найти

оптимальную стратегию на страховом рынке (сочетание своей

относительной рисковой надбавки, величины своего резерва с учетом

возможности инвестирования временно свободных средств, различных

вариантов перестраховочных договоров). Такой пример рассмотрен в /3/

где исследуется коллективная модель (портфель генерирует

пуассоновскй поток исков).

Замечание по квотному перестрахованию. Страховщик оставил

себе долю (

а) и передал на перестрахование долю (1 - а).

Тогда:

X=Y + Z, причем: Y = aX, Z = (1 - a)X, следовательно:

M(Y)=a × M(X),

D(Y)=a

× D(X),

Sy=a × Sx

M(Z)=(1-a) × M(X),

D(Z)=(1-a)

× D(X),

Sz=(1-a) × Sx.

Если бы Y и Z были бы независимы, то возник бы эффект:

D(Y) + D(Z) < D(X), из которого следовало бы уменьшение СКО/МО.

Но ситуация иная.

Y и Z связаны функционально: Z=Y × (1-a)/a.

Поэтому складываются не дисперсии, а СКО. Следовательно, общая

дисперсия сохраняется, тогда сохранится и СКО/МО. Так же, как и в

отдельности для

Y и Z.

Складывается впечатление, что никакого выигрыша нет! Однако

каждую сторону интересует только

своя дисперсия (т.е. ковариация

никакой роли не играет и потому не учитывается!). Следовательно,

неравенство выполняется (как это ни парадоксально) и тогда СКО растет

медленнее, чем МО. Возникает эффект, аналогичный объединению

субпортфелей.

219

12.4. Сравнение и графическая иллюстрация

различных перестраховочных договоров

Среди всех перестраховочных договоров наиболее простым

является договор о пропорциональном перестраховании. Пусть

основной договор предусматривает полное возмещение ущерба.

Страховая сумма

S равна рыночной цене. Пусть Х – размер

обоснованного иска, предъявленного страхователем страховщику.

Относительно этого риска есть договор о пропорциональном

перестраховании, согласно которому цедент платит часть возмещения в

объеме

Y = a*X, а Z = (1 – a)*X перестраховщик оплачивает остальное.

Ситуация проиллюстрирована на первом рисунке. Видно, что доля

цедента «

a» указывает тангенс угла наклона.

Рис 12.2

Рис 12.1

x=y+z

Перестраховщику практически неважно, как именно распределена

величина ущерба. Если он доверяет квалификации своего цедента, ему

нужны лишь условия основного контракта, т.к. и взносы и возмещения

делятся в оговоренной пропорции. Ситуация предельно упрощается,

если перестраховщик уступает своему цеденту комиссионные в размере

разности между относительными рисковыми надбавками

(перестраховщика и цедента).

Исключение составляет ситуация, когда страховая сумма

достаточно велика, а цедент стремится почти весь риск передать на

220

перестрахование. Это может возникнуть, если цедент принял данный

риск (невыгодный) в пакете с «выгодными» рисками, и хочет поправить

свои дела за счет перестраховщика. Здесь последний может потребовать,

чтобы уровень собственного удержания у цедента, был не ниже

определенного.

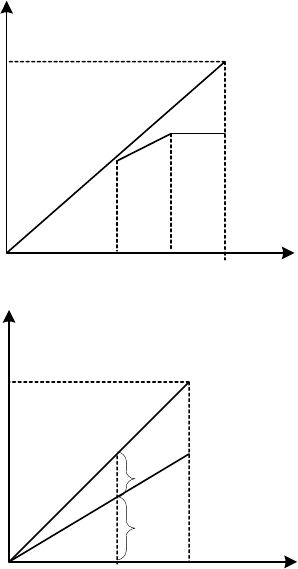
На втором рисунке представлена возможная модификация

договора. Здесь сначала ущерб возмещает только цедент, затем

следующую часть ущерба цедент и перестраховщик возмещают в

определенной пропорции, и наконец, если ущерб превышает

оговоренную величину, цедент платит лишь фиксированную сумму, а

весь ущерб сверх этой суммы возмещает перестраховщик.

Пропорциональный договор «перешел» в эксцедентный. На объем

ответственности влияет площадь фигур, однако, здесь перестраховщик

обязательно потребует от цедента информацию о распределении

величины ущерба. Потому, что задача может быть решена

«геометрически» только при равномерном распределении.

В общем же случае распределение отразится на оценках

параметров (МО и СКО), а следовательно, и на рисковой премии, и на

рисковой надбавке для перестраховочного договора.

Рис 12.3.а.

Рис 12.3.б.

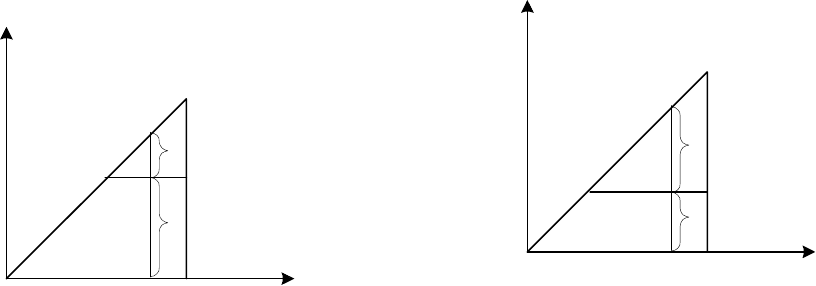
Цель эксцедентного договора, в некотором смысле, аналогична

безусловной франшизе – состоит в ограничении сверху ответственности

цедента на уровне собственного удержания r, передав на

перестрахование весь следующий риск (рис. 12.3.а, 12.3.б). Видно, что в

зависимости от выбора

r, при одном и том же ущербе страхователя X

доля цедента Y и доля перестраховщика Z – различны. Уменьшение r

приводит к возрастанию ответственности перестраховщика и,

соответственно, к росту цены перестраховочного договора. Однако,

перестраховщик не обязан принимать весь предлагаемый риск. В

эксцедентном договоре перестраховщик может ограничить свою

ответственность:

А) сверху: задав предел своей ответственности, тогда, если ущерб

превзойдет это значение, то весь ущерб сверх того компенсирует сам

цедент;