Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

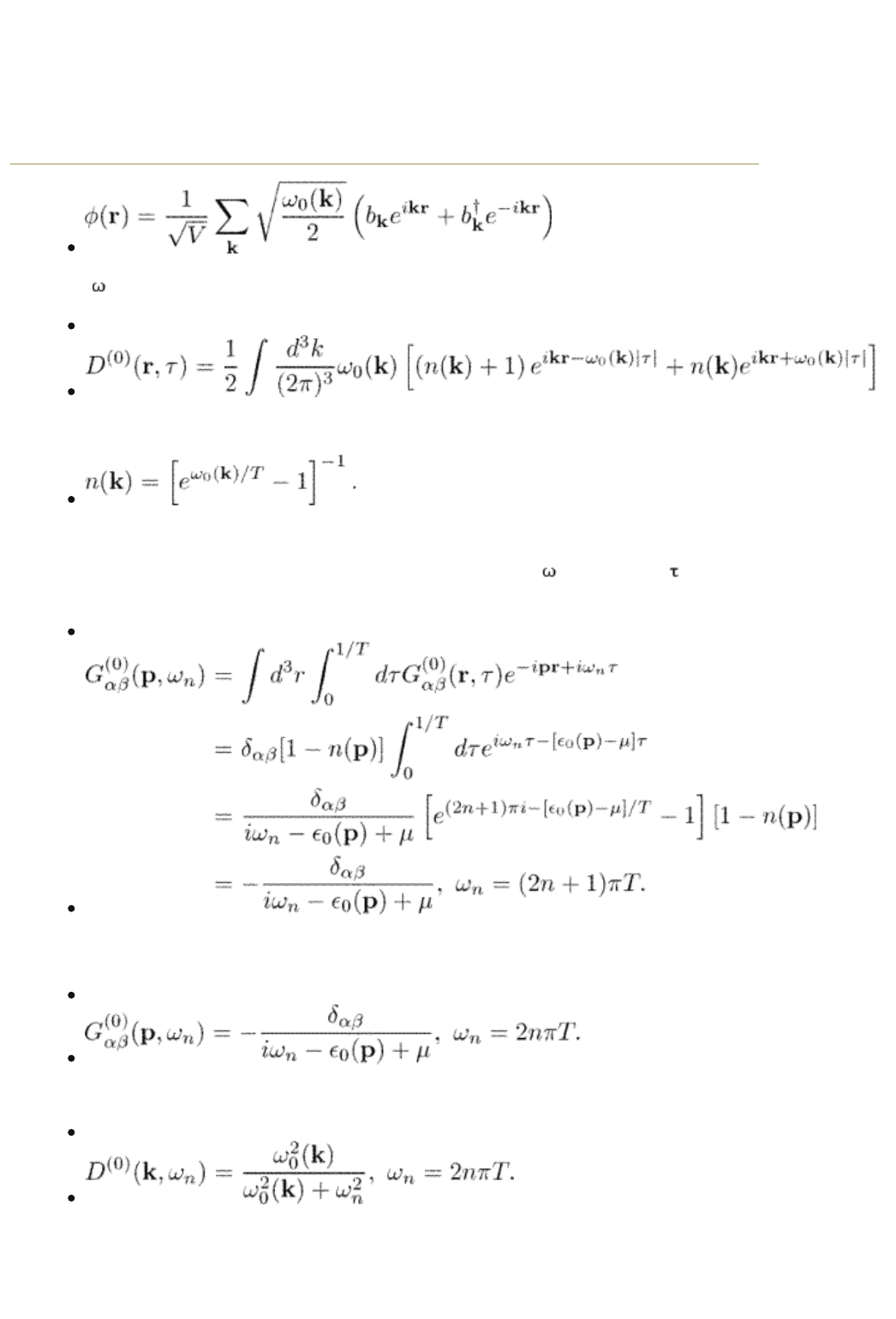
where

(k)is the phonon energy. The result is

(2.54)

where

It is useful to look at the free-particle Green function in the Fourier

representation. Consider a Fermi particle. To calculate G(p,

) we take G( > 0)

and use eqns (2.44) and (2.52). We have

(2.55)

For Bose particles we get

(2.56)

For phonons we have

(2.57)

2.2.3 The Wick theorem

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [36]-[40]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 10:57

Consider the statistical average

taken over the states of noninteracting particles. It is the sum over all the

quantum states. The wave functions of each state are normalized in such a way

that the normalization constant is proportional to

where V is volume of

the system. Therefore, the average has the form

end p.36

(2.58)

The matrix elements for the whole combination of a-operators are only nonzero if

there are equal numbers of creation and annihilation operators belonging to the

same state. For example, nonzero is the term

(2.59)

where the states with n m are different from all other quantum states. Nonzero

are also other terms which ran he obtained from eqn (2.59) by transpositions of

the indices n, m, etc. If there are four creation and annihilation operators

belonging to the same state the nonzero terms have the form

(2.60)

where n m. Expressions of the type of eqn (2.59) are different from all other

nonzero terms like eqn (2.60) in that the former have as many summation as

there are 1/V factors. All other terms have at least one extra factor 1/V. Since

the number of quantum states is proportional to the volume of the system, only

the terms of the type of eqn (2.59) remain finite in the limit of a large volume of

the system V

We come to the conclusion that, in the limit of V

, i.e., for a macroscopic

system, the statistical average of a combination of -operators is nonzero only if

the pairs of creation and annihilation operators

all belong to different

quantum states. This implies that the statistical average can be calculated for

each pair of operators

independently. Indeed, the Hamiltonian and the

particle-number operator of non-interacting particles, which both consist of pairs

of the aa

-operators, commute with any pair of aa if they all belong to different

states. Therefore,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 10:57

(2.61)

since Hamiltonian is an additive function for noninteracting particles. The fact

that all

are in the interval allows us to put the

exponents again before all the -operators.

In other words, the statistical average of a T

-product of a large number of

-and -operators is equal to the sum of T -products of all possible pair

averages. The sign of each term in the sum is + if the corresponding sequence of

end p.37

the -operators is obtained from the initial sequence by an even transposition,

and it is – if the required transposition is odd. This is the contents of the Wick

theorem. For example,

The Wick theorem is of crucial importance for the Green function technique.

Indeed, the Hamiltonian of the system is usually made up of various

combinations of the particle operators. If the particles interact, the Hamiltonian

contains the operators to powers higher than the second power. They come in

the exponent, and a general expression for the Green function is thus hopelessly

complicated. Here the Wick theorem saves the situation. We can expand the

exponent into the power series in the interaction Hamiltonian and obtain the sum

of terms which are various even powers of the particle operators. According to

the Wick theorem, each term can be reduced to a product of several Green

functions of noninteracting particles. As a result, we obtain an expression for the

full Green function of interacting particles as a series of terms containing powers

of the interaction strength and products of noninteracting Green functions

(Feynman diagrams). This allows one to find the full Green function to any

desirable accuracy in the interaction strength. In many cases, the summation of

such a series can be performed analytically, which results jn the so-called Dyson

equation for the full Green function. The Dyson equation is the central result for

the Green function technique because it provides the algorithm for calculation of

the Green function and thus of any physical observable of a complicated system

of interacting particles. A more detailed description of the diagram technique for

various systems can be found in the book by Abrikosov et al. (1965).

2.3. The real-time Green functions

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 10:57

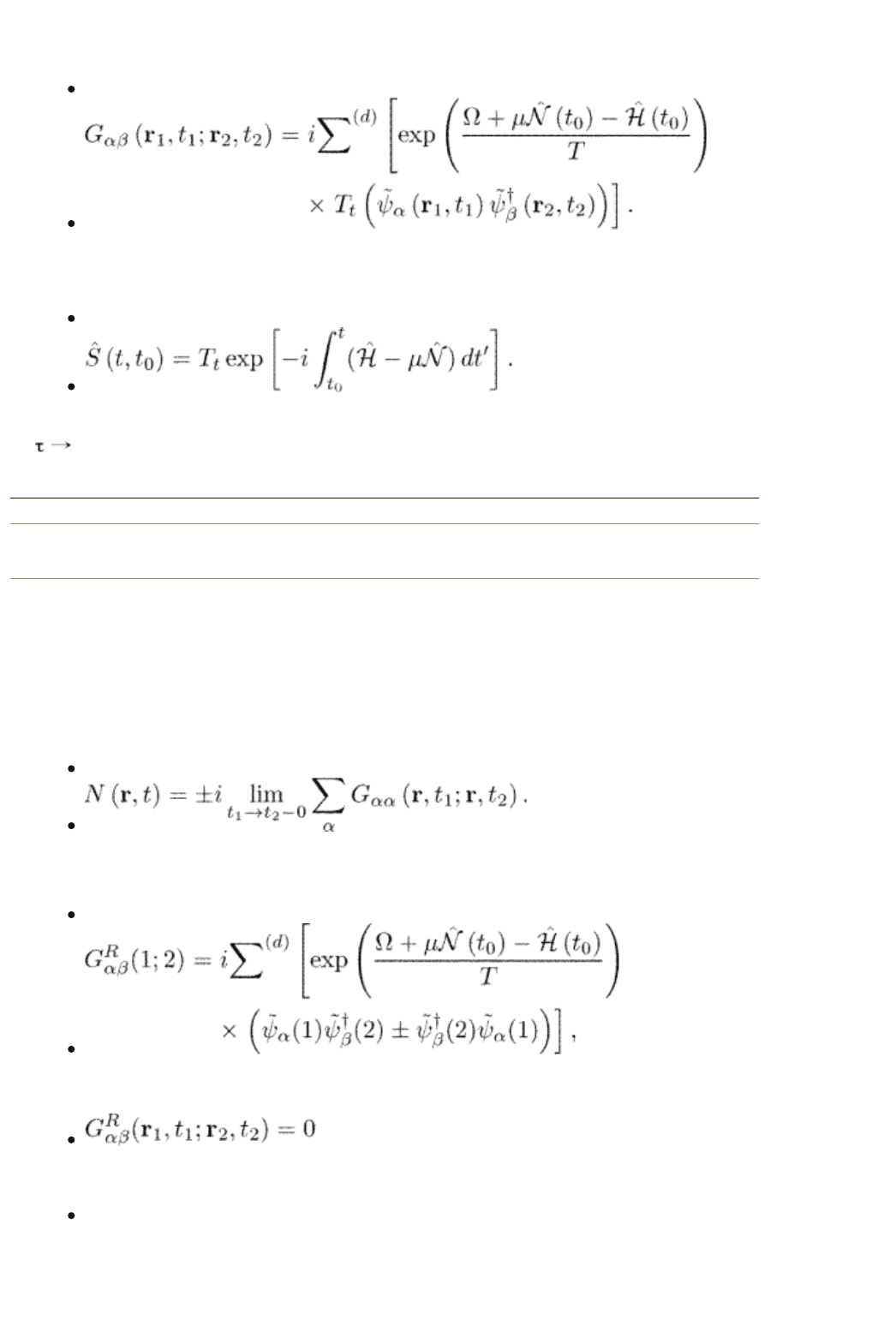
2.3.1 Definitions

The real-time Green function is defined as

(2.62)

The Heisenberg operators are determined through the real-time S-matrix which

is defined similarly to eqn (2.35)

(2.63)

The real-time S matrix can be obtained from eqn (2.35) by a formal substitution

it.

end p.38

The statistical average in eqn (2.62) is taken at a time instant t

. This definition

implies that, at the time t

, the system was in thermodynamic equilibrium; the

field operators evolve since then according to the Schrödinger equation or as

determined by the S matrix in eqn (2.63). Note that the Hamiltonian can now be

a function of time. The real-time Green function defines the density matrix and

thus it is this function which determines the physical quantities for a

time-dependent system. For example, the particle density is

(2.64)

We define also the so-called retarded G

and advanced G

Green functions:

(2.65)

for t

> t

and

for t

< t

. Similarly,

(2.66)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 10:57

for t

< t

and

for t

> t

2.3.2 Analytical properties

Consider the Fourier transformed retarded Green function

(2.67)

We assume for simplicity that the Hamiltonian does not depend on time. The

Fourier transformed Green function G

( ) is an analytical function of in the

upper half-plane of complex . Indeed, in this case we can calculate the integral

in eqn (2.67) for t

< 0 by shifting the contour of integration into the upper

half-plane of

. Since G

( ) is analytical, the integral vanishes, and we have

, t

) = 0 for t

< t

as it should be according to the definition. Similarly,

( ) is an analytical function of in the lower half-plane.

end p.39

We now want to prove that the Matsubara functions are coupled to the retarded

and advanced functions through

(2.68)

(2.69)

To do this we note that the matrix elements of the Heisenberg operators are

(2.70)

where

(2.71)

with N

= N

± 1. Therefore, for t > 0 according to eqn (2.65)

(2.72)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 10:57

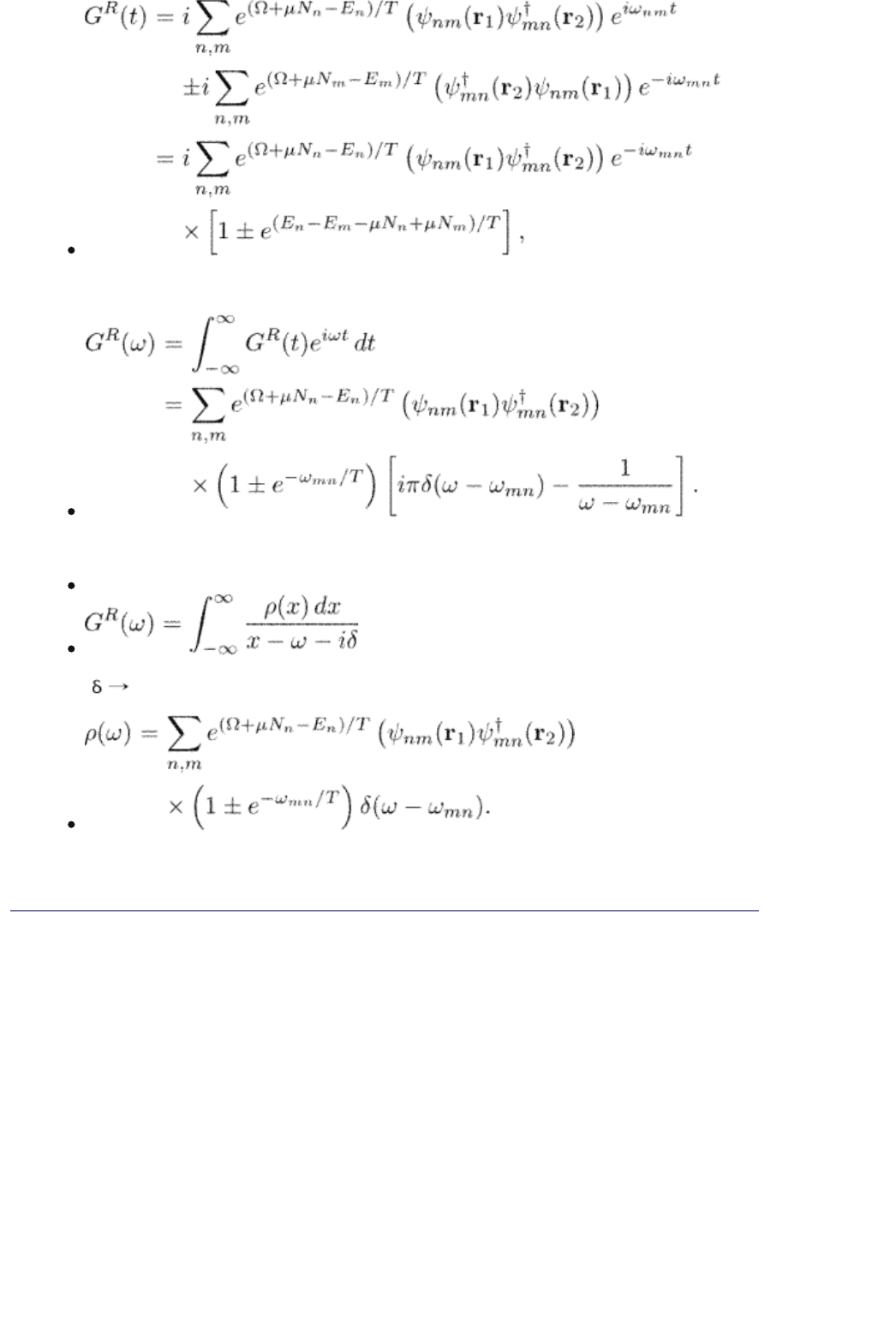
and G

(t) = 0 for t < 0. For the Fourier transforms we have

Therefore,

(2.73)

where 0 and

During the derivation we use the identity

end p.40

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 10:57

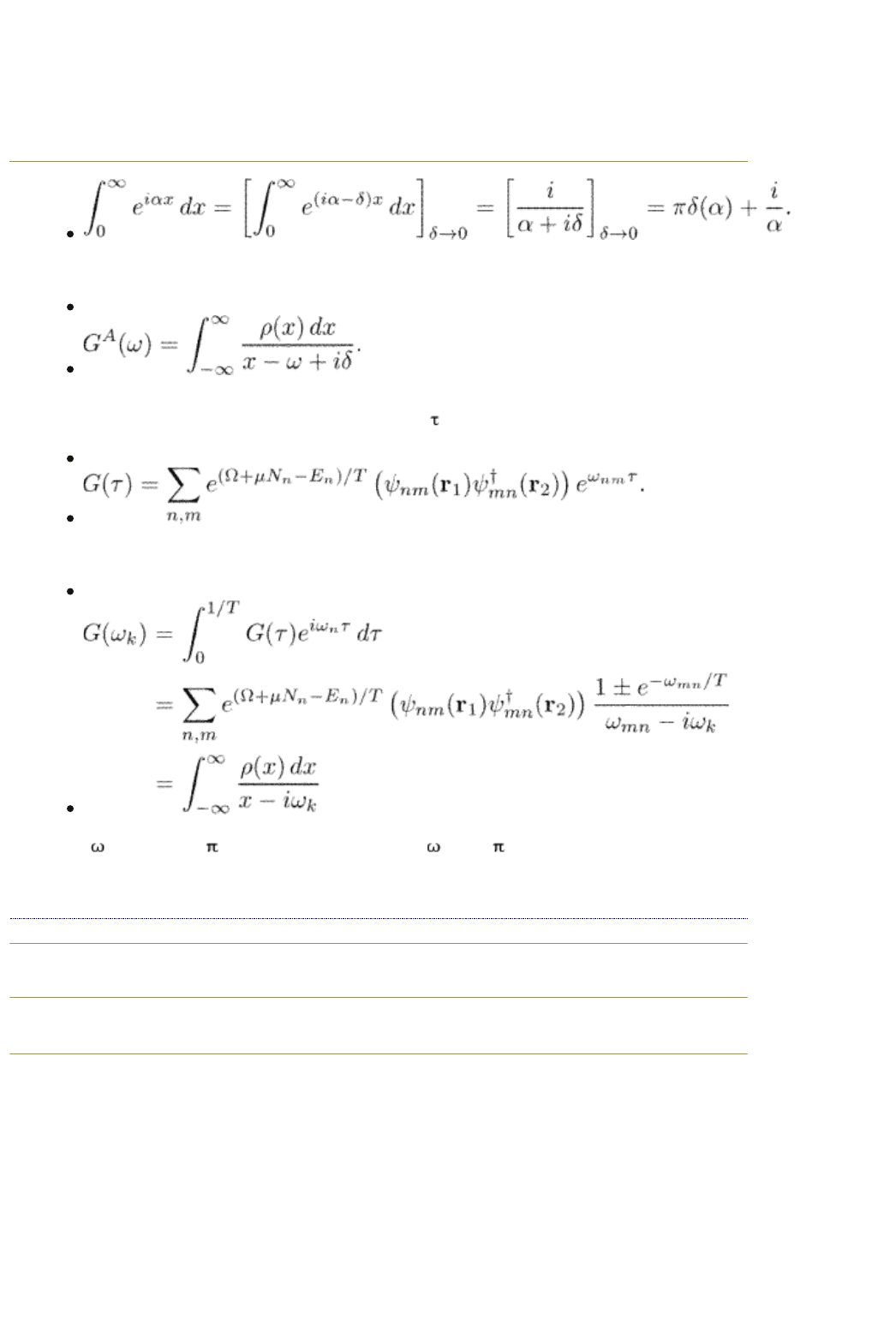
In the same way we get

(2.74)

For the Matsubara Green function, we have for > 0

(2.75)

This gives

(2.76)

where

= (2k + 1) T for Fermi particles and

= 2k T for Bose particles.

Comparing eqns (2.73) and (2.74) with (2.76) we arrive at eqn (2.69).

end p.41

3 THE BCS MODEL

Nikolai B. Kopnin

Abstract: This chapter applies the Green function formalism to the BCS theory

of superconductivity — the Gor'kov equations are derived which make the basis

for the further analysis. The Green functions are used to derive the expressions

for such physical quantities as the superconducting order parameter, the electric

current, the electron density, and the thermodynamic potential. The

Bogoliubov–de Gennes equations are derived from the Gor'kov equations. The

Gor'kov theoy is used to derive the Green functions in a homogeneous state, the

gap function, the critical temperature, the supercurrent, etc.

Keywords: Gor'kov equations, Bogoliubov-de Gennes equations, order

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [41]-[45]

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共5页 2010-8-8 11:00

parameter, supercurrent, critical temperature

We apply the Green function formalism to the Bardeen–Cooper–Schrieffer

theory of superconductivity and derive the Gor’kov equations which make

the basis for our analysis. We couple the Green functions to such physical

quantities as the order parameter of the superconductor, the electric

current, the electron density, and the thermodynamic potential. We derive

the Bogoliubov–de Gennes equations from the Gor’kov equations. Several

applications of the Gor’kov theory are considered.

3.1 BCS theory and Gor’kov equations

The BCS Hamiltonian (Bardeen et al. 1957) contains the attractive interaction

between electrons. This attraction is needed for electrons to form Cooper pairs

which then condense into a superconducting state. We consider a

spin-independent interaction. This leads to a zero-spin (spin-singlet)

superconducting state which is what one usually has in real superconductors. The

Fermi statistics of electrons requires a spin-singlet state to have an even parity

with respect to the transposition of the particle coordinates or (which is the

same) with respect to inversion of the relative momentum of particles. This

means that the super-conducting state should be of either s-wave or d-wave (or

of other higher-order even) symmetry in the relative momentum of particles. We

start our consideration with the s-wave superconducting state and will consider

some specifics of a d-wave state later.

There can be various physical mechanisms of attraction between electrons. In the

phonon model, for example, the attraction is mediated by an exchange of

phonons. The pairing interaction usually works in a restricted energy range and

vanishes for energy transfer larger than some cut-off value

BCS

. In case of

phonons, the interaction is effective only when the exchange of energy is less

than the characteristic Debye frequency

. If the interaction is relatively weak

the characteristic energies of particles participating in the superconducting

phenomena, are much smaller than both the Fermi energy and the cut-off

frequency

BCS

. In this case, a point-like interaction between the electrons in the

form

is a reasonable approximation. An attraction corresponds to g < 0. The limit of

small interaction corresponds to

where is the density of stales at the

Fermi level in the normal state. It is called a weak-coupling approximation.

end p.42

Let us derive the equations for the Green functions for the BCS model following

Gor’kov (1958) and, Abrikosov et al. (1965). The BCS Hamiltonian is

(3.1)

The Hamiltonian and the particle number operator

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共5页 2010-8-8 11:00

can be written through the Heisenberg operators which are defined in eqn (2.29).

Since

commutes with the Hamiltonian, the operators and in this

representation will have the same form as in eqns (3.1), (2.46).

Using eqn (2.31) we can calculate the time-derivative of the Heisenberg

operators

. Commuting with the Hamiltonian and the particle-number

operator taken at the same time we get

(3.2)

Here x = ( , r). The time-derivative of the Green function is

( G) denotes the Green function jump at

according to eqn (2.28). The

last line can be simplified using the Wick theorem:

end p.43

(3.3)

Here we need some discussion: First, we note that the decomposition of the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共5页 2010-8-8 11:00

four-operator average into a product of two averages of pairs of the operators is

strictly true for noninteracting particles according to the Wick theorem. Here we

perform the decomposition for real, and thus interacting, particles. There are two

major types of interaction. Interactions of one type are such that do not result in

the superconducting behavior. We neglect them. This is a model approximation;

the quality of the model should be considered separately for each particular case.

For example, it is not correct, of course, for a strongly correlated electron

system. However, for usual superconductors, where electrons form a Fermi liquid

with weak correlations, the BCS model proved to be very realistic. The

interaction of the second kind is the one which results in the superconducting

pairing. What we should have done with this interaction is to expand the average

of the four particle operators into the power series in the interaction strength g

and then to average each term using the Wick theorem. We would obtain the

series of diagrams containing the non-superconducting Green functions.

Performing summation of this series we would then obtain the full Green function

as it appears in eqn (3.3).

The second major feature of the model is as follows. The averages in the third

line in the r.h.s of eqn (3.3) do not disappear in the limit of a macroscopic

volume V

as it was assumed earlier during the derivation of the Wick

theorem. The reason is that now the average

(3.4)

contains a macroscopic number of particles because of the Cooper pairing effect:

due to a small attraction between electrons they form pairs which then condense

into a ground state. This is the basic assumption of the BCS theory. The average

of eqn (3.4) has the form of a wave function of the condensed Cooper pairs, i.e.,

of the superconducting electrons.

The first and the second terms in the r.h.s. of eqn (3.3) have the form

where

is called the self-energy. The self-energy leads to a renormalization of the

chemical potential

. In addition, it introduces a small imaginary part

proportional to the small g. In the BCS model, this relaxation term is ignored,

and the only effect of the interaction is assumed to be the pairing leading to a

nonzero average of the type of

. In the phonon model to be discussed in

Section 8.2, the self-energy is of the order of

; it is much smaller than

the characteristic superconducting energy in the so-called weak-coupling limit to

which we restrict

end p.44

our consideration. However, the relaxation part can be important for

nonstationary processes; we shall incorporate it where appropriate while

considering nonstationary phenomena throughout the book.

Dealing with the BCS model, we omit the self-energy from the expression for the

time-derivative of the Green function. Finally, we obtain

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共5页 2010-8-8 11:00