Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

where (x

– x

) = (

–

) (r

– r

). We define the new Green functions

(3.5)

(3.6)

They are called the “anomalous” or Gor’kov functions. We also define

(3.7)

Here we take into account that g < 0. The equation for the Green function

becomes

(3.8)

The function F (x

, x

) is odd in transposition of the particle coordinates and

spin indices because of the Fermi statistics of electrons. For a pairing interaction

which has an even parity in the orbital space such as an s-wave (or d-wave)

interaction, the Cooper pairing can only occur between the electrons with

opposite spin projections into a singlet state and the pair wave function is

antisymmetric in spin indices:

We can write

where

is the Pauli spin matrix. We also denote

Since our interaction does not depend on spin, the Green function G is

proportional to the unit matrix in the spin indices:

end p.45

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共5页 2010-8-8 11:00

As a result, we obtain from eqn (3.8)

(3.9)

This equation, contains an unknown function F and the quantity (x) which is

expressed through another unknown function F. To find these functions we need

more equations. The equation for F

can be obtained from the second eqn (3.2)

in a way similar to that used to derive eqn (3.9). We have

(3.10)

The equation for F contains the function

(3.11)

It is easy to see that

(3.12)

We have for F and :

(3.13)

and

(3.14)

Equations (3.9), (3.10), (3.13) and (3.14) form the system of generalized Dyson

equations for the BCS model. These equations are known as the Gor’kov

equations (Gor’kov 1958). The quantity

is called the order parameter. We

have already encountered it in Chapter 1. It has exactly the same meaning as in

the Landau theory of second-order phase transitions: it is zero in the

non-superconducting (normal) state and nonzero in a superconducting, state. It

is proportional to the wave function of superconducting electrons and thus is a

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [46]-[50]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 11:02

complex function. According to the definition of eqn (3.7), we have

(3.15)

This is a self-consistency equation: it couples the order parameter with the

function F which has to be found from equations containing

The function G(x

, x

) describes a particle moving from point x

to point x

while

describes a particle moving from point x

to point x

. The latter

particle is equivalent to a hole. According to eqn (3.12), the fact that the Gor’kov

equations contain

and on equal footing is a

manifestation of the particle–hole symmetry of the BCS theory.

end p.46

We can introduce the matrix Green function

(3.16)

and the matrix operator

where

(3.17)

These are called the matrices in the Nambu space. The Hamiltonian is now

measured from the chemical potential

. It is equivalent to of the

previous chapter. The four equations for the four Green functions can be written

in the compact matrix form

(3.18)

We can apply the operator to act on the second coordinate x

. To find the

corresponding equations, we multiply the derivatives of eqn (3.2) taken from the

functions of the coordinate x

by (x

) or (x

) from the left. After decoupling

of the averages using the Wick theorem we find for the BCS model

(3.19)

where the conjugated operator is

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 11:02

(3.20)

Here coincides with .

3.1.1 Magnetic field

In the presence of a magnetic field, the momentum operator should be replaced

with

(3.21)

when it acts on or , respectively. For a stationary electromagnetic field, the

scalar potential

can be incorporated into the chemical potential . Therefore, it

does not appear in stationary problems. The operator

becomes

(3.22)

where now

(3.23)

end p.47

The conjugated operator is

where

(3.24)

The electron-number density is

(3.25)

The electric current can be expressed through the Green functions using the

momentum density of eqn (2.48):

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 11:02

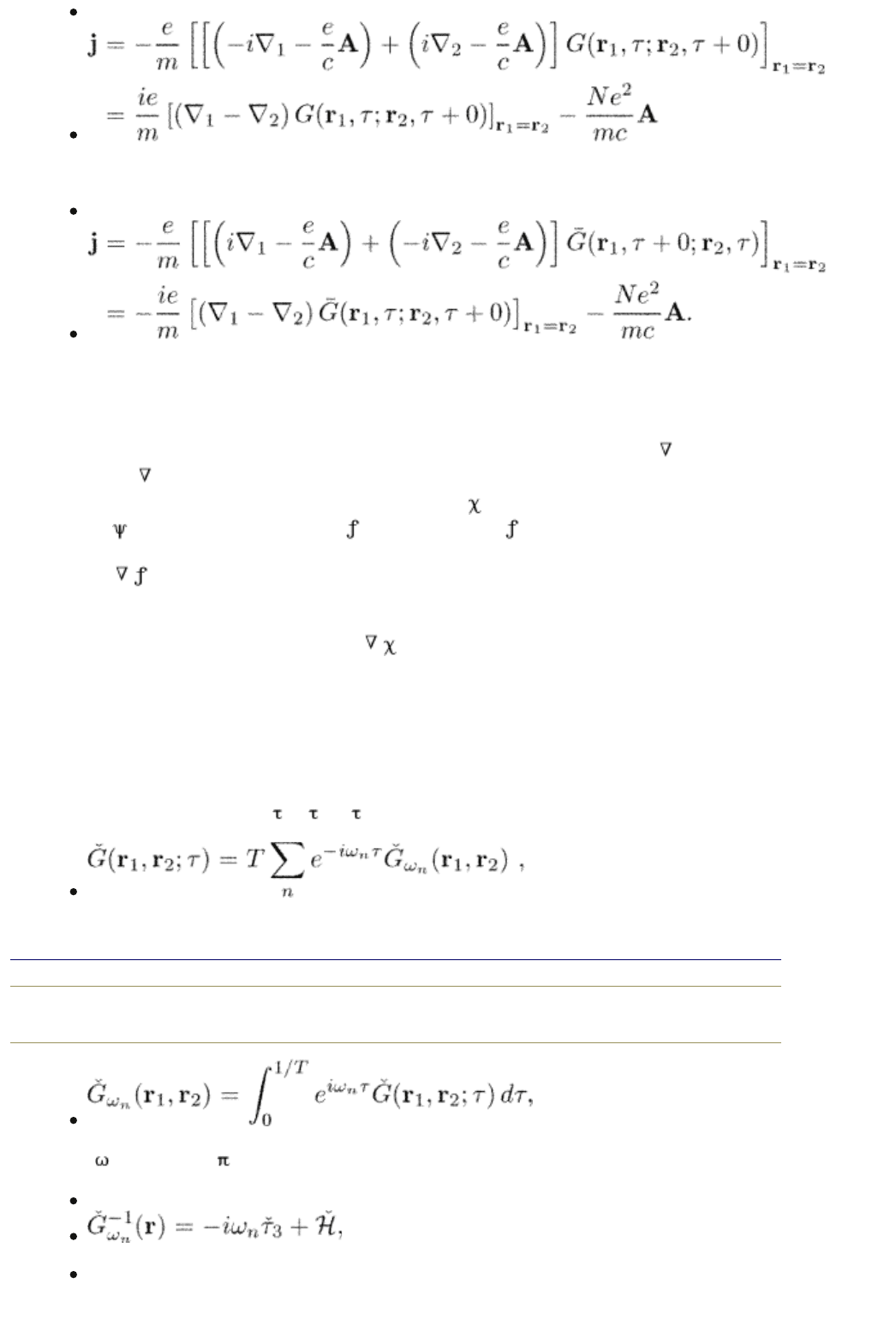
(3.26)

(3.27)

The factor 1/2 is canceled here due to summation over spin indices implied in the

definition, eqn (2.48).

The fact that the spatial derivatives enter the inverse operators for the Green

functions and the expressions for the electric current in combinations –i

–

(e/c)A and i

(e/c)A is a manifestation of the gauge invariance of the theory of

superconductivity. Indeed, a change in the phase

/2 of the single-electron wave

function

by an arbitrary function /2 results in the -change in the order

parameter phase: it can be compensated by the variation of the vector potential

by (c/2e)

. Since the magnetic field H = curl A does not change, the

superconducting state is invariant under the transformation of eqn (1.7) on page

4. Therefore, the vector potential should always appear in the combination with

the order parameter phase A – (c/2e)

to preserve the gauge invariance. This

gives a convenient test for checking whether the calculations which we are doing

are correct.

3.1.2 Frequency and momentum representation

Equations for the Green functions are more convenient in the frequency

representation. We denote

–

and write

end p.48

where

= (2n + 1) T. The operators are

(3.28)

(3.29)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 11:02

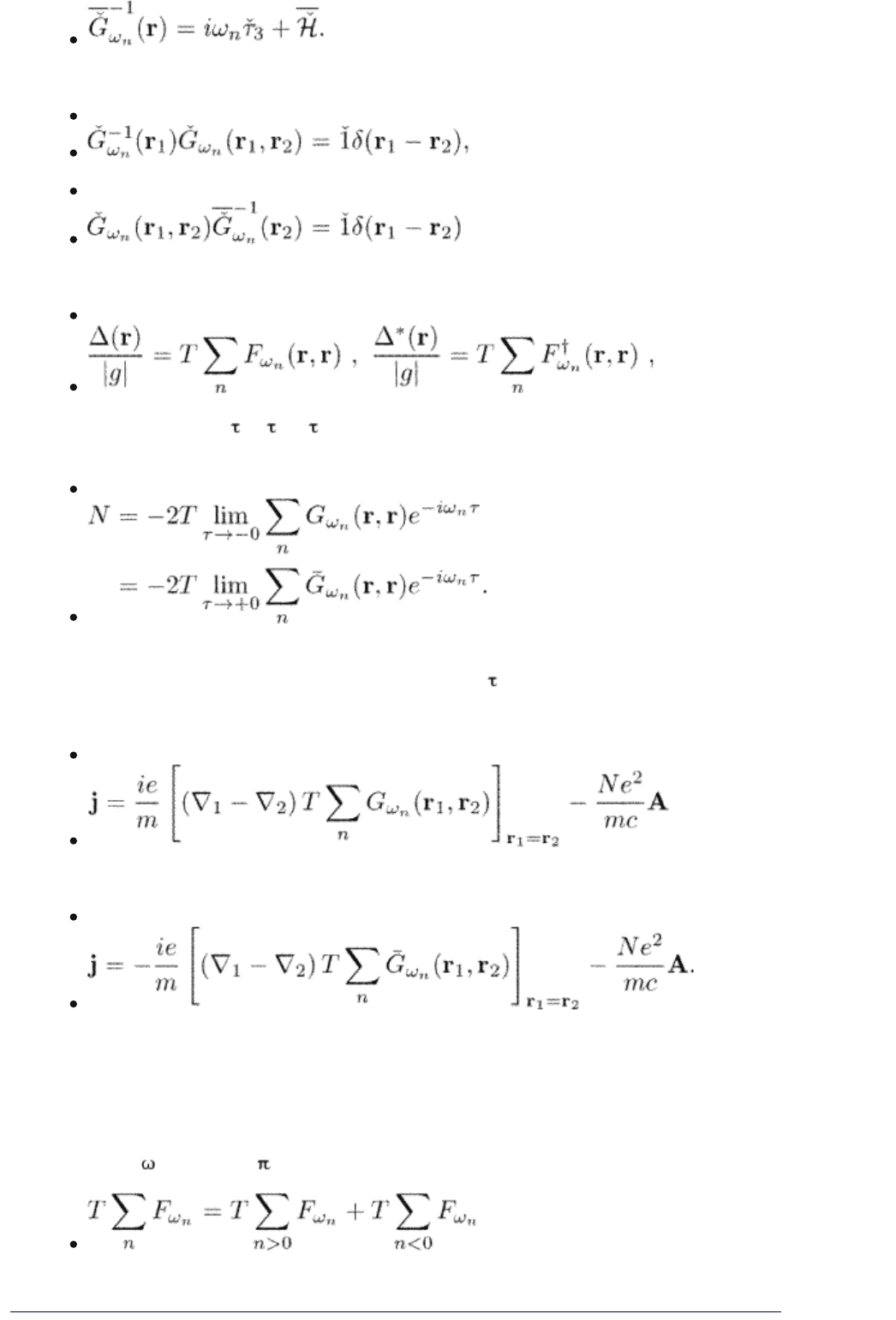
The matrix Gor’kov equation in the frequency representation is

(3.30)

(3.31)

The self-consistency equation for the order parameter becomes

(3.32)

since we have to take =

–

= 0. The electron density is obtained in a

similar way

(3.33)

The limits in eqn (3.33) need to be taken because G(r

, t

; r

, t

) is

discontinuous at (r

, t

) = (r

, t

) and the sums for = 0 do not converge.

The electric current becomes

(3.34)

(3.35)

The limiting procedure is not necessary for eqn (3.34) since the discontinuous

part vanishes as a result of action of the differential operators.

The order parameter equation and the expressions for the current and electron

density can be written in terms of the real-time retarded and advanced Green

functions, as well. We start with the order parameter equation. The sum over

frequencies

= (2n +1) T can be presented as

end p.49

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 11:02

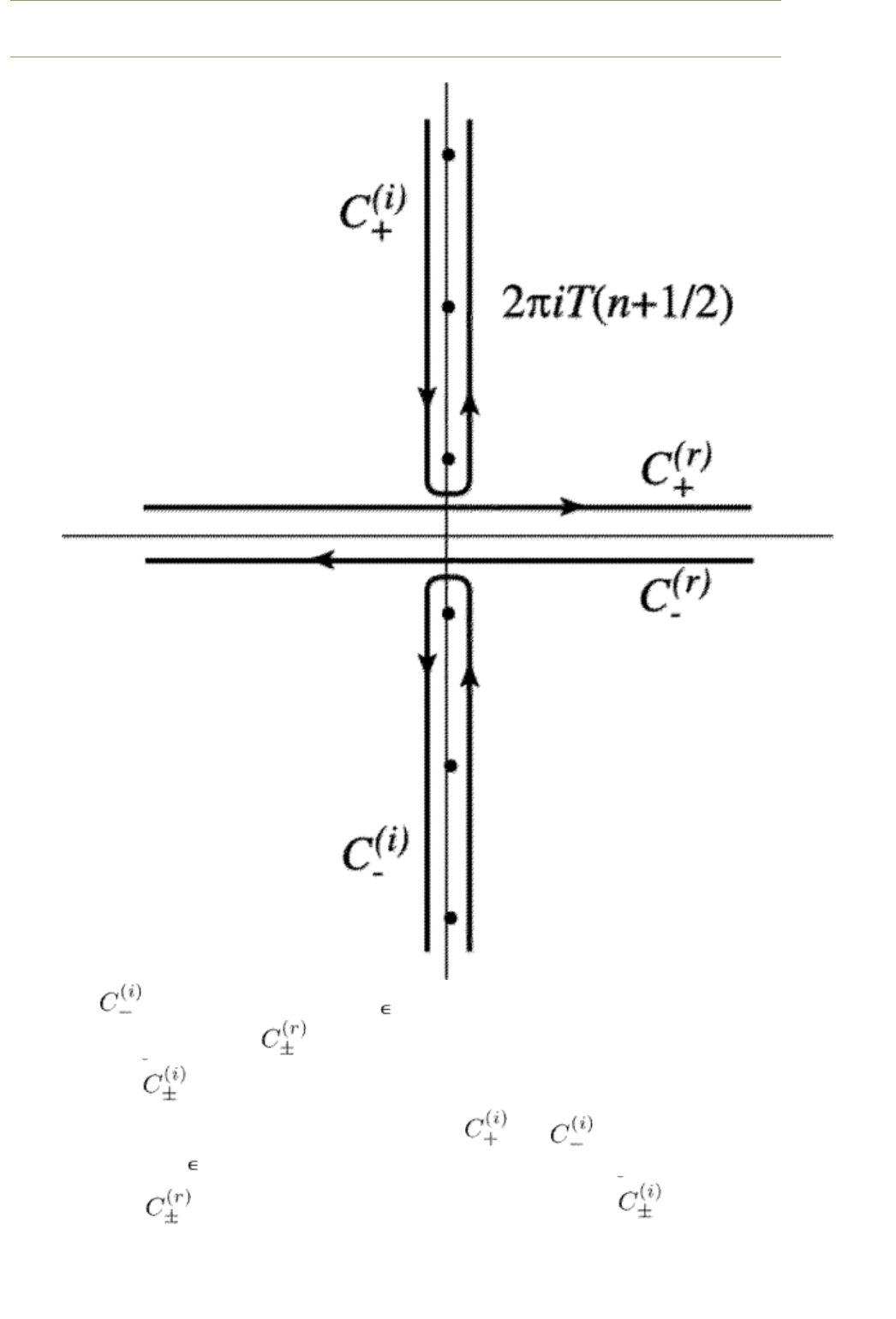
and encircle the poles of tanh ( /2T) in the upper (lower) half plane,

respectively. Contours

are obtained by shifting the respective

contours

onto the real frequency axis." title="Fig. 3.1. Contours of

integration over complex frequency. Contours

and encircle the

poles of tanh (

/2T) in the upper (lower) half plane, respectively.

Contours

are obtained by shifting the respective contours

onto the real frequency axis." class="figure">

IG. 3.1. Contours of integration over complex frequency.

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 11:02

Contours and encircle the poles of tanh ( /2T) in the

upper (lower) half plane, respectively. Contours

are

obtained by shifting the respective contours

onto the real

frequency axis.

The function tanh( /2T) has the poles at = (2n + 1) iT, i.e., at = i

. The

contour

encircles all the poles of tanh( /2T) in the upper complex

half-plane of

while the contour encircles all the poles of tanh( /2T) in the

lower complex half-plane of

(see Fig. 3.1). In the upper half plane, the function

is an analytical function and coincides with F

for = i

when

> 0. In

the same way, the function

is an analytical function in the lower half-plane

and coincides with F

for = i

when

< 0. We can now shift the contours in

such a way that

transforms into and goes along the real axis of from

to and transforms into which goes along the real axis of from

to + . Finally, we have

(3.36)

The order parameter equation becomes

(3.37)

The electric current is

end p.50

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 11:02

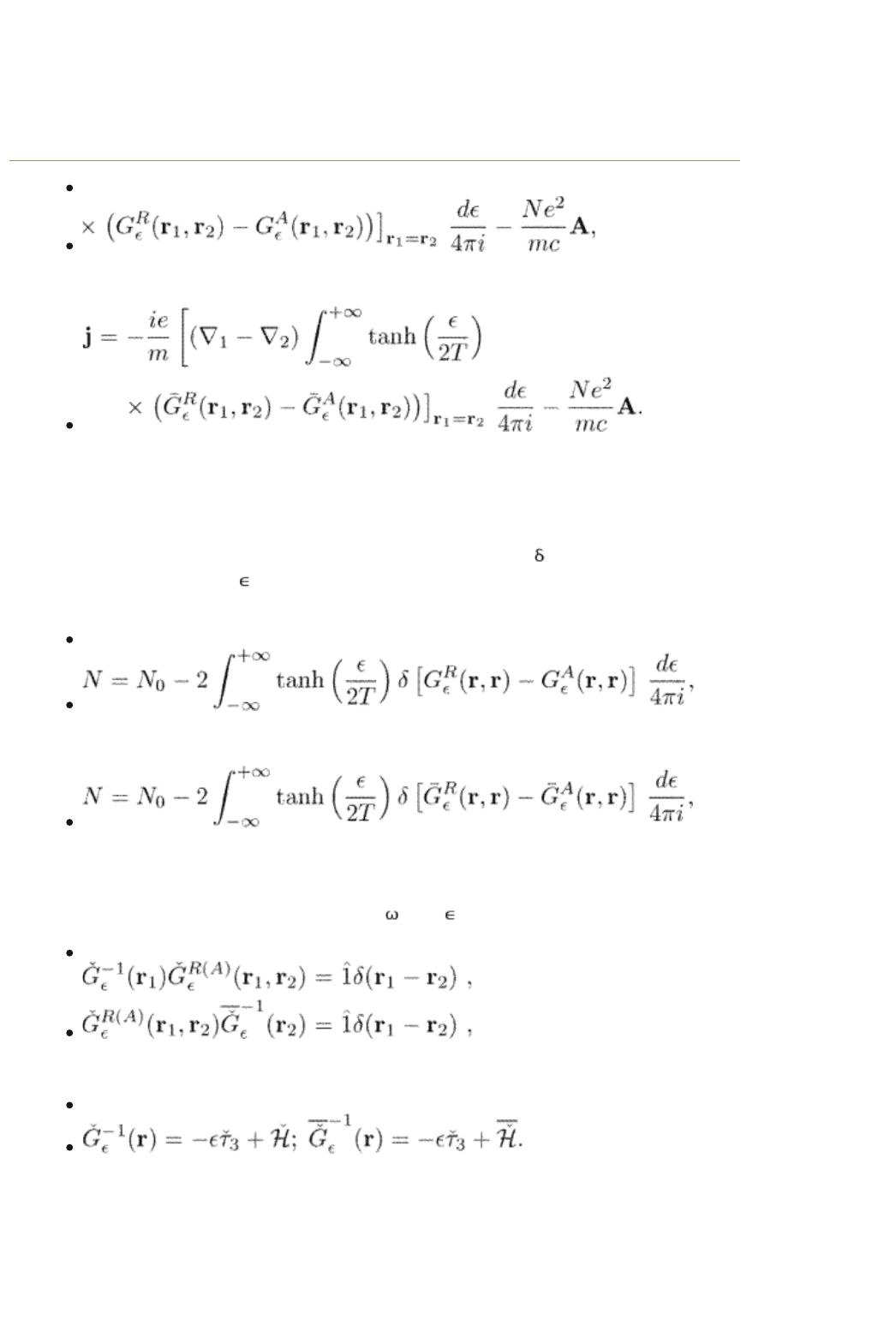
(3.38)

The transformation to the real frequencies for the electron density cannot be

performed straightforwardly because of the discontinuity of the corresponding

Green functions. The discontinuity results in a divergence of the integrals over

the remote contours. Let us first separate the contribution to the density from

the normal state. The remaining part of the Green functions

G then decreases

quickly enough for large , and the integrals over remote contours vanish. As a

result we obtain

(3.39)

where N

is the electron density in the normal state.

The retarded and advanced Green functions satisfy the same equations as the

Matsubara functions with the replacement

= –i :

(3.40)

where the inverse operators are

(3.41)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [51]-[55]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 11:04

The factor tanh( /2T) appears as a result of the replacement of the summation

over imaginary frequencies with integration over the real frequencies. It has a

simple physical meaning. Indeed,

(3.42)

where

is the Fermi distribution function expressed in terms of the energy measured

from the chemical potential.

end p.51

One can introduce the momentum representation of the Green function,

(3.43)

The particle–hole symmetry equation (3.12), in particular, implies

(3.44)

(3.45)

In the momentum–frequency representation, the order parameter equation

becomes

(3.46)

(3.47)

The current is

(3.48)

(3.49)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 11:04