Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

2.1.1 Schrödinger and Heisenberg operators

One can introduce the operators

(2.14)

Operator (x) creates a particle at the point x while (x) annihilates it. These

operators are called Schrödinger “particle-field” operators. We have

(2.15)

(2.16)

(2.17)

The upper sign is for Fermi particles while the lower is for Bose particles. The

coordinate x may also include spin. The operator

, which for definiteness is

taken to be dependent on spatial coordinates, can be written as

Here and are the spin indices.

Let the Hamiltonian be

. The wave function obeys the Schrödinger equation

(2.18)

Its solution can be symbolically written as

(2.19)

where

does not depend on t. A time-dependent matrix element of an operator

F is

(2.20)

This is the matrix element of the operator

(2.21)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 10:51

This operator is called the Heisenberg operator. Its convenience is in that now

one can use time-independent wave functions

to calculate time-dependent

matrix elements. The time dependence is transferred to the operators. The time

derivative of

(2.22)

Note that the commutation rules for Heisenberg operators taken at the same

time are the same as for the corresponding operators in Schrödinger

representation, since the exponential factors cancel in products of two operators.

end p.29

2.2. Imaginary-time Green function

2.2.1 Definitions

The imaginary-time (Matsubara) Green function is defined for imaginary time t =

i within the interval

as follows:

(2.23)

for

and

(2.24)

. Here (r) and are Schrödinger operators; the signs refer

to Fermi and Bose particles, respectively. Operators

and are the

Hamiltonian of the system and the particle-number operator. Operator

(d)

means the sum over all diagonal matrix elements both for all quantum states for

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 10:51

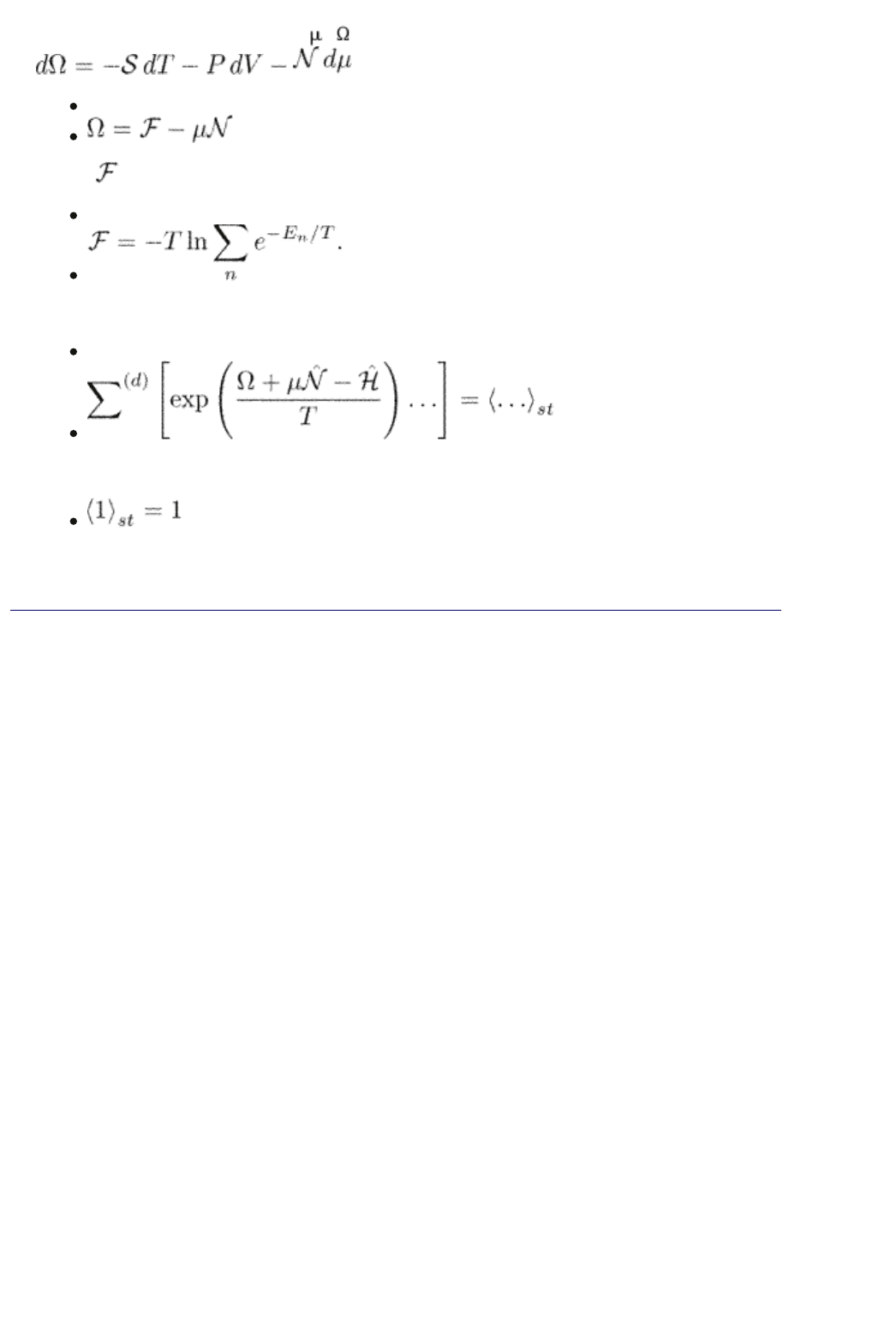
a given number of particles and for all numbers of particles. Thus G is a function

of T and the chemical potential

; is the thermodynamic potential:

. It is defined as

(2.25)

where is the free energy,

(2.26)

Therefore, the sum

(2.27)

is the Gibbs statistical average. Note that

due to the definitions of eqns (2.25) and (2.26).

end p.30

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 10:51

The phonon Green function is

for

and

for

The function G(

) experiences a jump at =

= 0. For Fermi

particles,

(2.28)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [31]-[35]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 10:51

Let us introduce the “Heisenberg” particle operators which depend on time . In

the representation with a given

we have

(2.29)

(2.30)

The Heisenberg operators satisfy the equations

(2.31)

Using this definition, we can write

(2.32)

Here T means ordering in : the -operators under T are placed from left to

right in order of decreasing “time”

. For Fermi particles we have

(2.33)

In the r.h.s., the -operators are put in the chronological order, and

takes +1

or – 1 depending on whether the transposition

end p.31

is even or odd. For example,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 10:51

The definition eqn (2.32) can be generalized to the case when the Hamiltonian

depends on time

explicitly. The Heisenberg operators are defined as

(2.34)

where we introduce the S-matrix

(2.35)

and

(2.36)

The operator orders times as they appear in the integral, i.e., first, comes the

time

then a time which is close to and lies between and 0, etc. Therefore,

We have for

Moreover

We also have

(2.37)

The Green function is now defined as

(2.38)

which coincides with eqn (2.32). It is very important to note that since the

Hamiltonian of the system is also constructed of the

operators, it is the use of

end p.32

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 10:51

imaginary time which allows us to place all the operators in proper positions

consistent with the T

operation. This is possible if the Green function is defined

within the time interval

where =

It is exactly

the reason why we consider an imaginary time: for a real time it is impossible to

define unambiguously the order of the

-operators.

There exists an important relation which couples G(

< 0) with G( > 0). Indeed,

if we make a cyclic transposition under the trace operator

(d)

, we obtain

Comparing it with eqn (2.23) for > 0, we see that

(2.39)

For phonons we get

(2.40)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 10:51

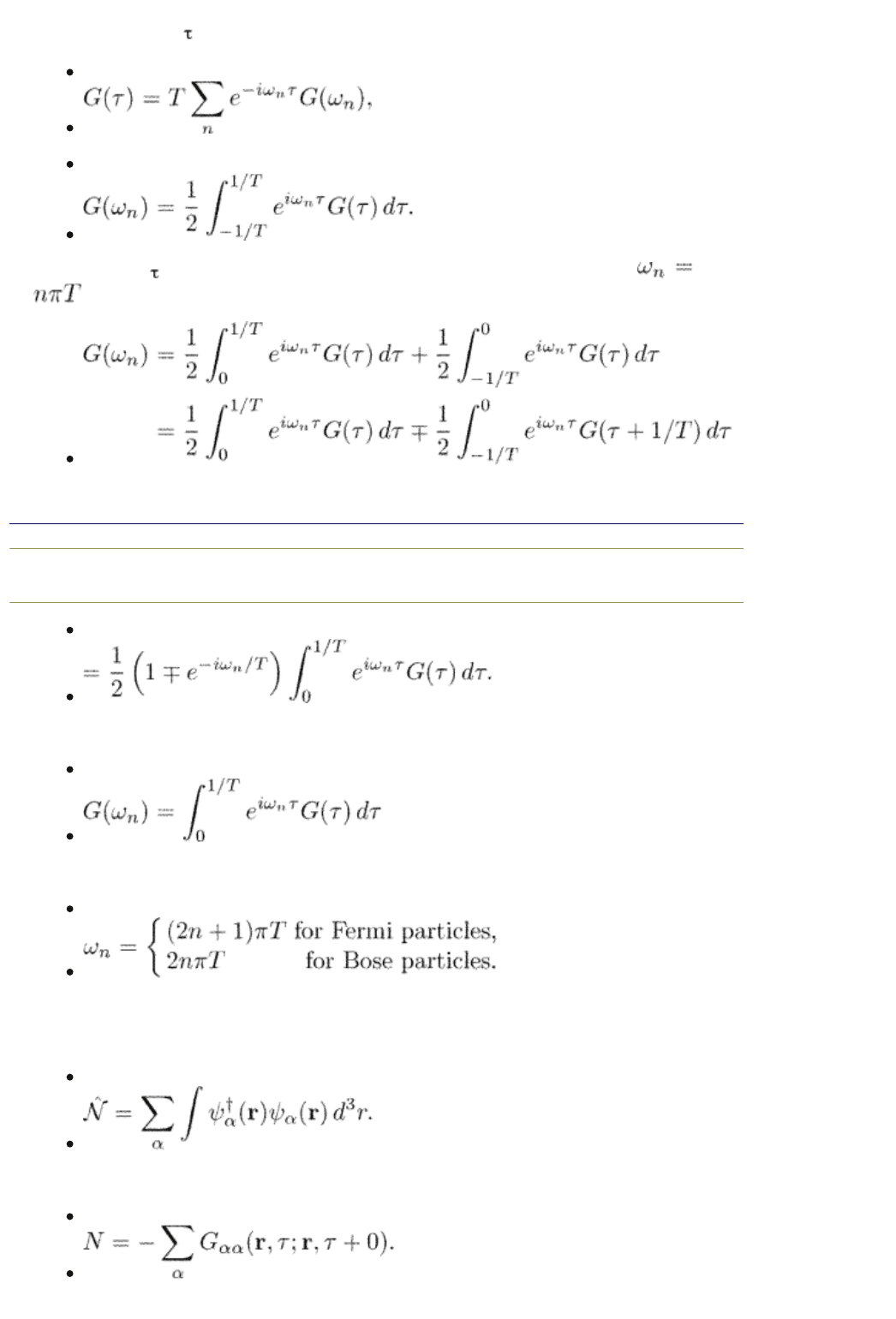
Equation (2.39) is of a great importance. Indeed, let us make a Fourier

transformation in

(2.41)

(2.42)

Because time is defined within a finite range, the frequency is discrete

. These frequencies are called the Matsubara frequencies. One has

end p.33

(2.43)

Therefore, the Fourier components

(2.44)

are nonzero only for

(2.45)

The Green function determines all properties of the system. For example, the

particle-number operator is

(2.46)

Thus, the particle density becomes

(2.47)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 10:51

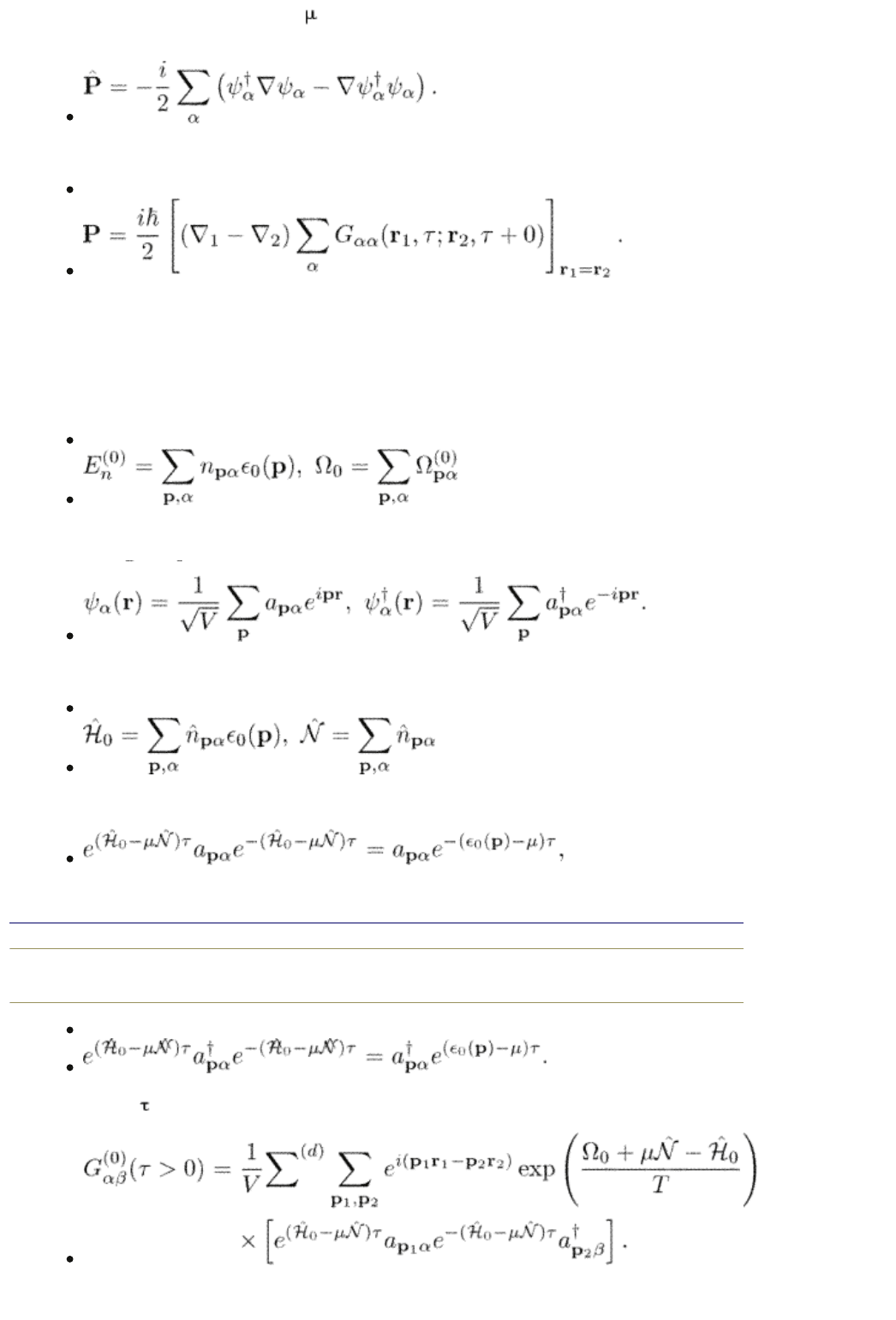
Using this equation one can find as a function of temperature, etc. The

momentum density operator is

Therefore, the momentum density is

(2.48)

2.2.2 Example: Free particles

For free noninteracting particles the statistical average is taken over the states of

every particle independently of other particles. The energy is

(2.49)

and the Schrödingor operators are

Since the Hamiltonian and the particle-number operators are

(2.50)

the creation and annihilation operators satisfy

end p.34

(2.51)

We have for > 0

As a result,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 10:51

since

The average for Fermi particles is

For Bose particles it is

In these equations, n(p) is the average equilibrium occupation number or the

distribution function which is different for Fermi and Bose particles.

We now take the limit V

using

and obtain

(2.52)

where r = r

– r

. For < 0 we write

(2.53)

The phonon Green function can be calculated in a similar way. The Schrödinger

operator is

end p.35

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 10:51