Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций

Подождите немного. Документ загружается.

До

столкновения j Момент^столнно^

После столмнобения

1 1

- М \ ® ! —' —

1 'i

I 1

срывнь/е

риношетные

р ! А В ! А

! ! ^ов ^

1 1

1 I 1

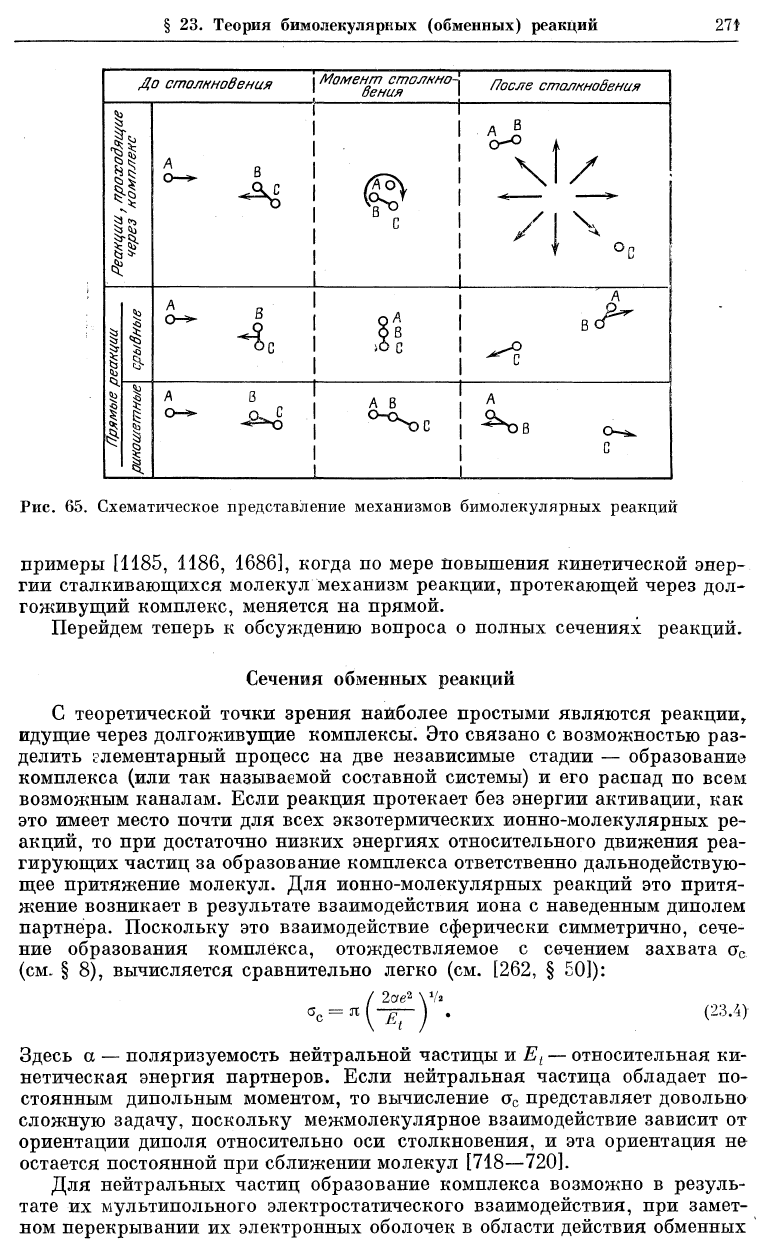
Рис. 65. Схематическое представление механизмов бимолекулярных реакций

примеры [1185, 1186, 1686], когда по мере повышения кинетической энер-

гии сталкивающихся молекул механизм реакции, протекающей через дол-

гоживущий комплекс, меняется на прямой.

Перейдем теперь к обсуждению вопроса о полных сечениях реакций.

Сечения обменных реакций

С теоретической точки зрения найболее простыми являются реакции,

идущие через долгоживущие комплексы. Это связано с возможностью раз-

делить элементарный процесс на две независимые стадии — образование

комплекса (или так называемой составной системы) и его распад по всем

возможным каналам. Если реакция протекает без энергии активации, как

это имеет место почти для всех экзотермических ионно-молекулярных ре-

акций, то при достаточно низких энергиях относительного движения реа-

гирующих частиц за образование комплекса ответственно дальнодействую-

щее притяжение молекул. Для ионно-молекулярных реакций это притя-

жение возникает в результате взаимодействия иона с наведенным диполем

партнера. Поскольку это взаимодействие сферически симметрично, сече-

ние образования комплекса, отождествляемое с сечением захвата о

(см. § 8), вычисляется сравнительно легко (см. [262, § 50]):

2ае

\Va

= ) • (23.4)

Здесь а — поляризуемость нейтральной частицы и E

— относительная ки-

нетическая энергия партнеров. Если нейтральная частица обладает по-

стоянным дипольным моментом, то вычисление а

представляет довольно

сложную задачу, поскольку межмолекулярное взаимодействие зависит от

ориентации диполя относительно оси столкновения, и эта ориентация не

остается постоянной при сближении молекул [718—720].

Для нейтральных частиц образование комплекса возможно в резуль-

тате их мультипольного электростатического взаимодействия, при замет-

ном перекрывании их электронных оболочек в области действия обменных

сил, либо же при образовании ионной пары, которая стабилизируется

переходом электрона с одной молекулы на другую. Если образование комп-

лекса сопряжено с преодолением потенциального барьера, то расчет обра-

зования составной системы требует детального знания той части поверхно-

сти потенциальной энергии, которая лежит на пути от исходных молекул

к комплексу. Одномерный профиль пути реакции такого типа показан на

рис. 26, б. Вершине потенциального барьера сопоставляется переходный

комплекс (активированное состояние), введение которого иногда облегча-

ет расчет сечения захвата. Потенциальной яме сопоставляется долгоживу-

щий комплекс, в котором происходит перераспределение энергии между

различными степенями свободы. Это перераспределение может быть опи-

сано движением изображающей точки только внутри многомерной потен-

циальной ямы, поэтому одномерная схема реакции является крайне услов-

ной.

После образования комплекса вероятности его распада могут быть рас-

считаны в рамках достаточно хорошо разработанной теории мономоле-

кулярных реакций, поскольку по существу долгоживущий комплекс ни-

чем не отличается от активной молекулы. Вероятность распада по некото-

рому каналу i определяется через константу скорости распада к

{

(Е) со-

отношением

Р.(Е) = К.(Е)1^К;(Е), (2.3.5)

где Е обозначает полную энергию комплекса, а величины к

{

(Е) вычисля-

ются по формулам § 19. Сечение реакции по каналу i выражается через се-

чение образования комплекса а

) и вероятность распада Р

{

(Е) — фор-

мулой:

E)=--e

(E).

(23.6)

Если в реакции (23.1) имеется всего два канала распада комплекса —

в направлении реакции (константа к

) и в обратном направлении (/с_

то выражение для сечения реакции принимает вид:

С(Е„ Е) =

0С(

Я,)

AL(£)

(

L) • (23.7)

Эта формула получена на основе упрощенных предположений, игно-

рирующих зависимость констант от полного углового момента комплекса.

При точных расчетах эта зависимость должна быть, конечно, учтена (см.

[262, § 31). Тем не менее, выражение (23.7) демонстрирует основную осо-

бенность реакций, протекающих через образование комплекса: сечение ре-

акции зависит только от относительной кинетической энергии E

полной энергии Е сталкивающихся молекул. Этот вывод доступен непо-

средственно экспериментальной проверке. Более того, неизменность сече-

ния при вариации распределения внутренней энергии партнеров (при неиз-

менном Е) является важнейшим аргументом в пользу статистического ха-

рактера распределения энергии.

Для экзотермических реакций, протекающих при энергиях, малых по

сравнению с теплотой реакции, энергия над порогом распада в экзотерми-

ческом направлении заметно превышает энергию распада в эндотермиче-

ском направлении. В этом случае к

(Е) ^> к.

(.Е), так что сечение реакции

в экзотермическом направлении просто совпадает с сечением образования

комплекса,

—

с• (23.8)

Для реакции в обратном направлении при той же полной энергии сечение

сг_! оказывается намного меньше сг

[262, § 31].

Примерами достаточно подробно экспериментально и теоретически ис-

следованных реакций, протекающих через образование долгоживущих

комплексов, могут служить процессы

R+ +

На

- н+ + Н

С+ + Da CQ+ + D,

первый из которых экзотермичен, второй — эндотермичен. Расчет сече-

ний первой реакции проводился в работах [260, 1684], второй — в работе

[1607].

Переходя к прямым реакциям, отметим, что реакции срыва допускают

более простую трактовку, чем рикошетные. В частности, для реакций сры-

ва А + ВС

—к

АВ -J- С было обнаружено, что переход атома В от молеку-

лы ВС к атому А почти не сопровождается отдачей, и поэтому скорость ато-

ма С до и после столкновения изменяется мало. Для таких реакций, иду-

щих по механизму «наблюдатель — срыв» (поскольку атом С фактически

является только наблюдателем, а не участником реакции), оказывается

возможным сравнительно просто вычислить угловое и энергетическое рас-

пределения продуктов и таким образом подвергнуть проверке основные

предположения о кинематике процесса.

Угловое распределение продуктов* характерное для срывных реакций,

может быть обусловлено взаимодействиями различных видов/ Для реак-

ции щелочных металлов М с молекулами галогенов Х

М. Полани еще в

1935 г. и Маги в 1940 г. (см. [498]) предложили модель реакции с переходом

электрона, позднее получившей название «модели гарпунирования» [372]:

при сближении М и Х

на некотором расстоянии происходит перескок

электрона, приводящий к образованию ионной пары М

— Х

. Затем

отрицательный ион Х

диссоциирует S поле положительного иона М

;

образующаяся при этом ионная пара М

Х~ представляет собой молекулу

MX : М + Х

->- М

+ Х

MX + X (подробности см. в работах [504,

1113]). Эта модель позволяет оценить порядок величины сечения реакции.

Переход электрона происходит на расстоянии Н

, которое соответствует

квазипересеченйю начальной ковалентной поверхности потенциальной

энергии с ионной поверхностью пары М — Х

(см. § 10). Условие квази-

пересечения записывается в виде равенства кулоновского притяжения ио-

• нов и разности потенциала ионизации /м атома М и электронного сродства

АХ

молекулы Х

: '

/Д

= /

- (23.9)

Полагая, что каждое образование ионной пары ведет к реакции, получим:

а=лЯ

. (23.10)

Таким образом, эта модель предсказывает независимость сечения реакции

от относительной энергии молекул и увеличение сечения при уменьшении

разности /м:

—

АХ

. ВычислениеR

из уравнения (23.9) показывает, что пере-

ход электрона происходит на расстоянии порядка 10 А. Вследствие боль-

ших значений R

столкновения с прицельным параметром превышающим

, ведут только к упругому рассеянию молекул. Отсутствие каких-либо

неупругих процессов, конкурирующих с упругим рассеянием и реакцией,

позволяет оценивать сечение реакции по искажению дифференциального

сечения рассеяния. Именно при малых углах рассеяния, соответствующих

прицельным параметрам Ъ R

дифференциальное сечение упругого

18 В. Н. Кондратьев, Е. Е. Никитин

рассеяния следует классическому закону, справедливому для потенциала

взаимодействия U (R) = — C

/i?

(см. § 8) [372]:

При некотором значении угла Ф = ^ и Ъ — R

происходит резкое па-

дение интенсивности рассеяния, которое следует интерпретировать как

следствие начала реакции. Соответствующий этому значению угла при-

цельный параметр определяет сечение реакции обмена. Выраженное через

угол Фс сечение реакции равно [482]:

а = (^-С

/а

(Я^сГ'Ч (23.12)

Измерение сечений гарпунных реакций подтверждает следствие, выте-

кающее из простой модели, об увеличении сечения при уменьшении потен-

циала ионизации атома щелочного металла (табл. 18). Эта модель предска-

Таблица 18

Корреляция сечений гарпунных реакций с потенциалами ионизации

атомов щелочных металлов (при E

= 0,12 эв) [482, 728]

Партнеры

, as o, A*

Партнеры

, эв

о, A*

К + J

4,32

125—140

Na+ J

5,138

Rb+ J

4,176

167

Na' + J

3,04

210

Cs+ J

3,87

180-195

зывает далее независимость сечения реакции от относительной кинетиче-

ской энергии молекул. Что касается внутреннего состояния молекулы

, то оно может влиять на сечение реакции только вследствие зависимо-

сти электронного сродства Х

от начального колебательного состояния.

Для рикошетных: реакций сечение обычно существенным образом зави-

сит от энергии относительного движения и внутренних состояний реаги-

рующих партнеров. В настоящее время имеется большое число работ по

расчету сечений (или вероятностей) реакций такого типа. Основная цель

этих работ состоит в установлении корреляции сечения реакции с особен-

ностями поверхностей потенциальной энергии. Результаты таких расче-

тов, допускающие наиболее простую интерпретацию, относятся к реакции

Н + Н

->Н

+ Н,

поскольку поверхность потенциальной энергии этой реакции отличается

особенно простой структурой. Сечение реакции зависит от трех парамет-

ров — относительной кинетической энергии E

и начальных значений вра-

щательного (j) и колебательного (и) квантовых чисел молекулы Н

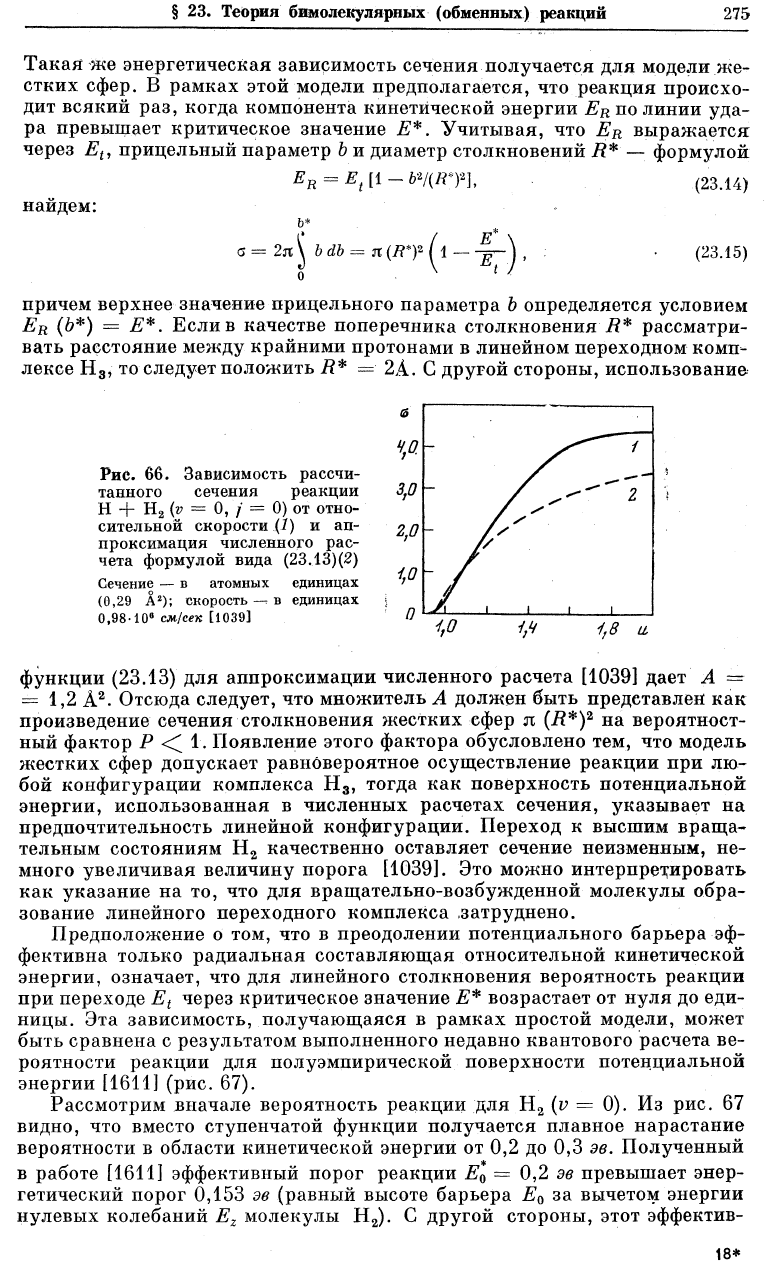
Квазиклассический численный расчет сечения реакции для основного

колебательного и вращательного состояния Н

дает монотонно-возрастаю-

щую функцию энергии E

от порога .Е*, величина которого меньше энергии

активации Еа, фигурирующей в методе переходного состояния (рис. 66,

кривая 1) [1039]. Если рассматривать Е* как некоторый эффективный

барьер, то приближенно сг может быть описано функцией (пунктир на

рис. 69, кривая 2):

в (E

/. = 0, у = 0) — Л (1 — EVE

(23

.13)

E*/E

< 1.

Такая же энергетическая зависимость сечения получается для модели же-

стких сфер. В рамках этой модели предполагается, что реакция происхо-

дит всякий раз, когда компонента кинетической энергии E

по линии уда-

ра превышает критическое значение Е*. Учитывая, что E

выражается

через Е

прицельный параметр

и диаметр столкновений i?* — формулой

= Е. [1 - Ъ*/(1ГП

найдем:

ь*

' =

2л;

db = я (i?*)

—

(23.14)

(23.15)

причем верхнее значение прицельного параметра

определяется условием

ER (Ь*) = Е*. Если в качестве поперечника столкновения /?* рассматри-

вать расстояние между крайними протонами в линейном переходном комп-

лексе Н

, то следует положить i?* — 2А. С другой стороны, использование

Рис. 66. Зависимость рассчи-

танного сечения реакции

Н + Н

(v = 0, / = 0) от отно-

сительной скорости (1) и ап-

проксимация численного рас-

чета формулой вида (23.13)(2)

Сечение — в атомных единицах

(0,29 А

); скорость —г в единицах

0,98-10® см/сек [1039]

-f

}

8 LL

функции (23.13) для аппроксимации численного расчета [1039] дает А ~

= 1,2 А

. Отсюда следует, что множитель А должен быть представлен как

произведение сечения столкновения жестких сфер л (В*)

на вероятност-

ный фактор Р 1. Появление этого фактора обусловлено тем, что модель

жестких сфер допускает равновероятное осуществление реакции при лю-

бой конфигурации комплекса Н

, тогда как поверхность потенциальной

энергии, использованная в численных расчетах сечения, указывает на

предпочтительность линейной конфигурации. Переход к высшим враща-

тельным состояниям Н

качественно оставляет сечение неизменным, не-

много увеличивая величину порога [1039]. Это можно интерпретировать

как указание на то, что для вращательно-возбужденной молекулы обра-

зование линейного переходного комплекса .затруднено.

Предположение о том, что в преодолении потенциального барьера эф-

фективна только радиальная составляющая относительной кинетической

энергии, означает, что для линейного столкновения вероятность реакции

при переходе E

через критическое значение Е* возрастает от нуля до еди-

ницы. Эта зависимость, получающаяся в рамках простой модели, может

быть сравнена с результатом выполненного недавно квантового расчета ве-

роятности реакции для полуэмпирической поверхности потенциальной

энергии [1611] (рис. 67).

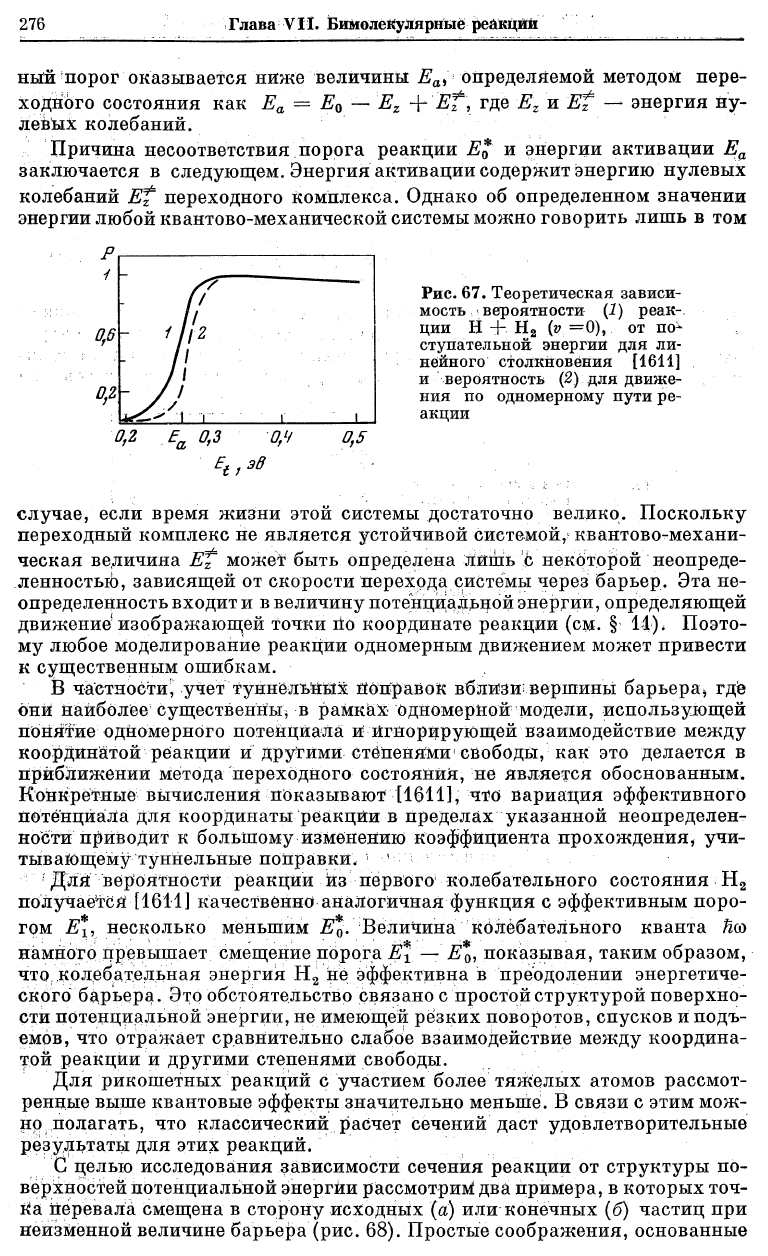
Рассмотрим вначале вероятность реакции для Н

(v = 0). Из рис. 67

видно, что вместо ступенчатой функции получается плавное нарастание

вероятности в области кинетической энергии от 0,2 до 0,3 эв. Полученный

в работе [1611] эффективный порог реакции Е

= 0,2 эв превышает энер-

гетический порог 0,153 эв (равный высоте барьера Е

за вычетом энергии

нулевых колебаний E

молекулы Н

). С другой стороны, этот эффектив-

ный порог оказывается ниже величины Е

аь

определяемой методом пере-

ходного состояния как Е

= Е

— E

+ Ef , где E

и Ef — энергия ну-

левых колебаний.

Причина несоответствия порога реакции Е* и энергии активации Е

заключается в следующем. Энергия активации содержит энергию нулевых

колебаний Ef переходного комплекса. Однако об определенном значении

энергии любой квантово-механической системы можно говорить лишь в том

Рис. 67. Теоретическая зависи-

мость вероятности (1) реак-

ции Н +. Н

(v —0), от по^

стунательной энергии для ли-

нейного столкновения [1611]

и вероятность (2) для движе-

ния по одномерному пути ре-

акции

случае, если время жизни этой системы достаточно велико. Поскольку

переходный комплекс не является устойчивой системой, квантово-механи-

ческая величина Ef может быть определена лишь с некоторой неопреде-

ленностью, зависящей от скорости перехода системы через барьер. Эта не-

определенность входит и в величину потенциальной энергии, определяющей

движение изображающей точки rio координате реакции (см. § 11)

Поэто-

му любое моделирование реакции одномерным движением может привести

к существенным ошибкам.

В частности

•

учет туннельных йоправок вблизи вершины барьера* гдё

они наиболее существенны* в рамках одномерной модели, использующей

понятие одномерного потенциала и Игнорирующей взаимодействие между

координатой реакции и другими степенями свободы, как это делается в

приближении метода переходного состояния, не является обоснованным.

Конкретные вычисления показывают [1611], что вариация эффективного

потенциала для координаты реакции в пределах указанной неопределен-

ности приводит к большому изменению коэффициента прохождения, учи-

тывающему туннельные поправки, >

Для вероятности реакции из первого колебательного состояния Н

получается [1611] качественно аналогичная функция с эффективным поро-

гом Е*, несколько меньшим 2?*. Величина колебательного кванта /гсо

намного превышает смещение порога Е\ — Е*

0г

показывая, таким образом,

что. колебательная энергия Н

не эффективна в преодолении энергетиче-

ского барьера. Это обстоятельство связано с простой структурой поверхно-

сти потенциальной энергии, не имеющей резких поворотов, спусков и подъ-

емов, что отражает сравнительно слабое взаимодействие между координа-

той реакции и другими степенями свободы.

Для рикошетных реакций с участием более тяжелых атомов рассмот-

ренные выше квантовые эффекты значительно меньше. В связи с этим мож-

но полагать, что классический расчет сечений даст удовлетворительные

результаты для этих реакций.

С целью исследования зависимости сечения реакции от структуры по-

верхностей потенциальной энергии рассмотрим два примера, в которых точ-

ка перевала смещена в сторону исходных (а) или конечных (б) частиц при

неизменной величине барьера (рис. 68). Простые соображения, основанные

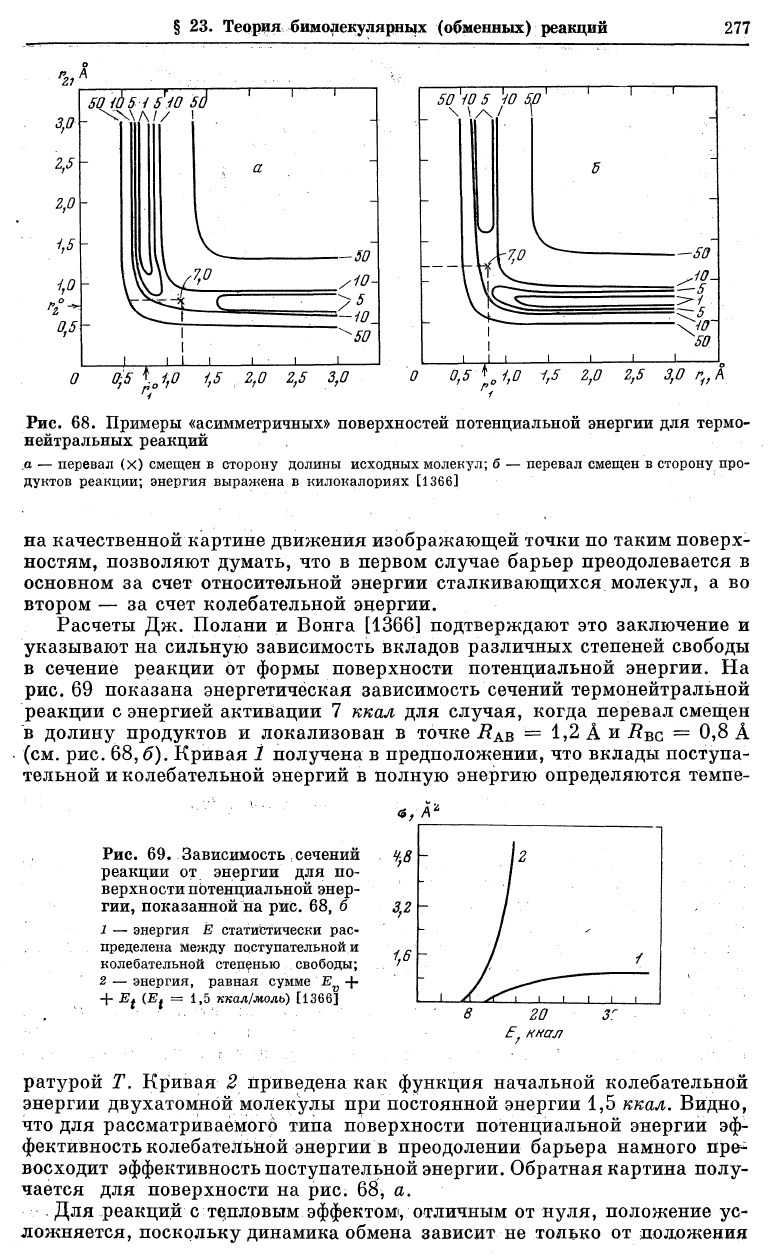
а — перевал (х) смещен в сторону долины исходных молекул; б — перевал смещен в сторону про-

дуктов реакции; энергия выражена в килокалориях [1366]

на качественной картине движения изображающей точки по таким поверх-

ностям, позволяют думать, что в первом случае барьер преодолевается в

основном за счет относительной энергии сталкивающихся молекул, а во

втором — за счет колебательной энергии.

Расчеты Дж. Полани и Вонга [1366] подтверждают это заключение и

указывают на сильную зависимость вкладов различных степеней свободы

в сечение реакции от формы поверхности потенциальной энергии. На

рис. 69 показана энергетическая зависимость сечений термонейтральной

реакции с энергией активации 7 ккал для случая, когда перевал смещен

в долину продуктов и локализован в точке i?

= 1,2 А и с = 0,8 А

(см. рис. 68,б). Кривая 1 получена в предположении, что вклады поступа-

тельной и колебательной энергий в полную энергию определяются темпе-

А*

Рис. 69, Зависимость сечений

реакции от энергии для по-

верхности потенциальной энер-

гии, показанной на рйс. 68, б

1 — энергия Е статистически рас-

пределена между поступательной и

колебательной степенью свободы;

2 — энергия, равная сумме E

+ E

= 1,5 ккал/моль) [1366]

ратурой Т. Кривая 2 приведена как функция начальной колебательной

энергии двухатомной молекулы при постоянной энергии 1,5 ккал. Видно,

что для рассматриваемого типа поверхности потенциальной энергии эф-

фективность колебательной энергии в преодолении барьера намного пре-

восходит эффективность поступательной энергии. Обратная картина полу-

чается для поверхности на рис. 68, а.

. Для реакций с тедлрвым эффектом, отличным от нуля, положение ус-

ложняется, поскольку динамика обмена зависит не только от положения

и нал

барьера, но и от того, какая из долин соответствует более низкой энергии

[1063,1358а].

Исследование этого вопроса [1266, 1336, 1361] в рамках полуэмпири-

ческого метода показывает, что для экзотермических реакций при умень-

шении энергии активации барьер сдвигается в сторону исходных молекул.

Эта корреляция, совместно с ранее обсуждавшимся соотношением между

энергией активации и теплотой реакции (см. §11), устанавливает связь

между теплотой реакции и положением активационного барьера, позволяя,

таким образом, сделать некоторые качественные заключения о зависимо-

сти сечения реакции от поступательной и колебательной энергий молекул

в ряду однотипных реакций обмена. Именно для экзотермических реак-

ций наиболее эффективной в преодолении активационного барьера должна

быть поступательная энергия молекул, а для эндотермических — колеба-

тельная. Разумеется, в таком общем виде это утверждение справедливо

лишь качественно, и от него возможны отступления, обусловленные кон-

кретными особенностями динамики реакции.

Одна из таких особенностей, называемая аномалией легкого атома [970,

1109, 1362], состоит в том, что колебательная энергия молекулы BG в эн-

дотермической реакции обмена А+ ВС —AB-f- С не эффективна в прео-

долении потенциального барьера, если масса атома В намного меньше

массы атомов А и С. В результате сечение реакции оказывается сравни-

тельно слабо зависящим от колебательного состояния ВС.

Распределение энергии по степеням свободы

в продуктах реакции

Распределение энергии по степеням свободы продуктов реакции (23.1)

зависит от распределения энергии по степеням свободы реагирующих мо-

лекул и от деталей взаимодействия атомов в промежуточном комплексе.

Распределение энергии характеризуется функцией распределения по со-

стояниям возникающих молекул, пропорциональной скорости их образо-

вания в заданном состоянии. Соответствующая константа к

1ш

выражается

через сечение реакции c

}lm

(u) и начальные функции распределения

I т

= 2 lm(«) /а («а) /в (»в)

"A *U

. (23.16)

Здесь через г, j обозначена совокупность начальных квантовых чисел реа-

гирующих молекул; и — их относительная скорость, через I, т — сово-

купность квантовых чисел молекул — продуктов реакции. Современные

методы экспериментального исследования реакций позволяют во многих

случаях измерять функции распределения, и одна из задач теории состоит

в том, чтобы по известным функциям распределения получить информа-

цию относительно сечений реакций.

В общем случае по величине к

1т

нельзя восстановить сечение c

ylm

Однако для экзотермических реакций, в которых выделяющаяся энергия

намного превосходит среднюю энергию реагирующих молекул, можно ожи-

дать, что

будет слабо зависеть от функций распределения ХА, ХВ, /А,

. Тогда без большой погрешности усреднение по начальным состояниям

можно опустить, заменяя квантовые числа Z, j и скорость и их наиболее

вероятными значениями jf, й. В этом случае (23.16) принимает вид:

к = (Z), (23.17)

1 ш

что позволяет выразить сечение реакции а

{

ilm

через функцию распределе-

ния возникающих молекул.

Поскольку сечения прямого и обратного процессов связаны соотношением

детального равновесия (8.38), выражение (23.17) может быть использовано

для вычисления сечения эндотермической реакции как функции кванто-

вых чисел Z, т при условии постоянства полной энергии. Таким образом,

может быть получена ценная информация относительно зависимости сече-

ний эндотермической реакции от энергии индивидуальных степеней сво-

боды реагирующих молекул. Такого рода расчет, выполненный для реак-

ции HF + Н = F + Н

— 34 7

ккал

[1365] и реакций НС1 + J HJ +

+ CI — 33,9 ккал и НС1 + С1 ->- Н + С1

— 48,6 ккал [413] на основании

экспериментальных функций распределения энергии по степеням свободы

в обратных реакциях, показывает, что сечение увеличивается на порядки,

если большая часть энергии является колебательной энергией исходных

молекул. Эти примеры подтверждают сделанный ранее вывод о том, что в

преодолении энергетического порога эндотермической реакции основную

роль играет колебательная энергия реагирующих молекул.

Теоретический расчет распределения энергии реакции по степеням сво-

боды молекул в общей постановке задачи сталкивается с теми же трудностя-

ми, что и расчет сечений. Исключение представляют лишь реакции, проте-

кающие через образование долгоживущих комплексов. В этом случае ста-

тистическая теория позволяет сравнительно просто получить функции рас-

пределения. Такого рода расчеты выполнены для ряда ионно-молекуляр-

ных реакций [809, 1271, 1685], а также для некоторых реакций, идущих с

участием нейтральных частиц [1153, 1609, 1610].

Для прямых реакций простые результаты можно получить лишь путем

значительного упрощения модели. Длясрывных реакций А + ВС-*- АВ +

+ С такое упрощение состоит в том, что атом С считается лишь «наблюда-

телем» процесса, и его скорость не меняется при переходе атома В к атому

А (см. выше). Такое предположение соответствует тому,что основной вклад

в сечение рассеяния дают малые углы (предельный случай рассеяния впе-

ред, характерного для реакций срыва). В этом случае закон сохранения

полного импульса однозначно определяет относительную кинетическую

энергию возникающих молекул, для которой оказывается справедливым

выражение:

= E

-E

=-E

2 т

+ га

(23.18)

где E

и E

— энергия исходных частиц и продуктов реакции.

Отсюда на основании закона сохранения полной-энергии получаем

следующее выражение для полной внутренней энергии молекул — продук-

тов реакции:

AZ?

BH = (23.19)

Вопрос о распределении внутренней энергии по степеням свободы не может

быть решен в рамках этой простой модели.

Уточнение этой модели путем учета небольшого притяжения партне-

ров в начальном и конечном состояниях [940] приводит к появлению до-

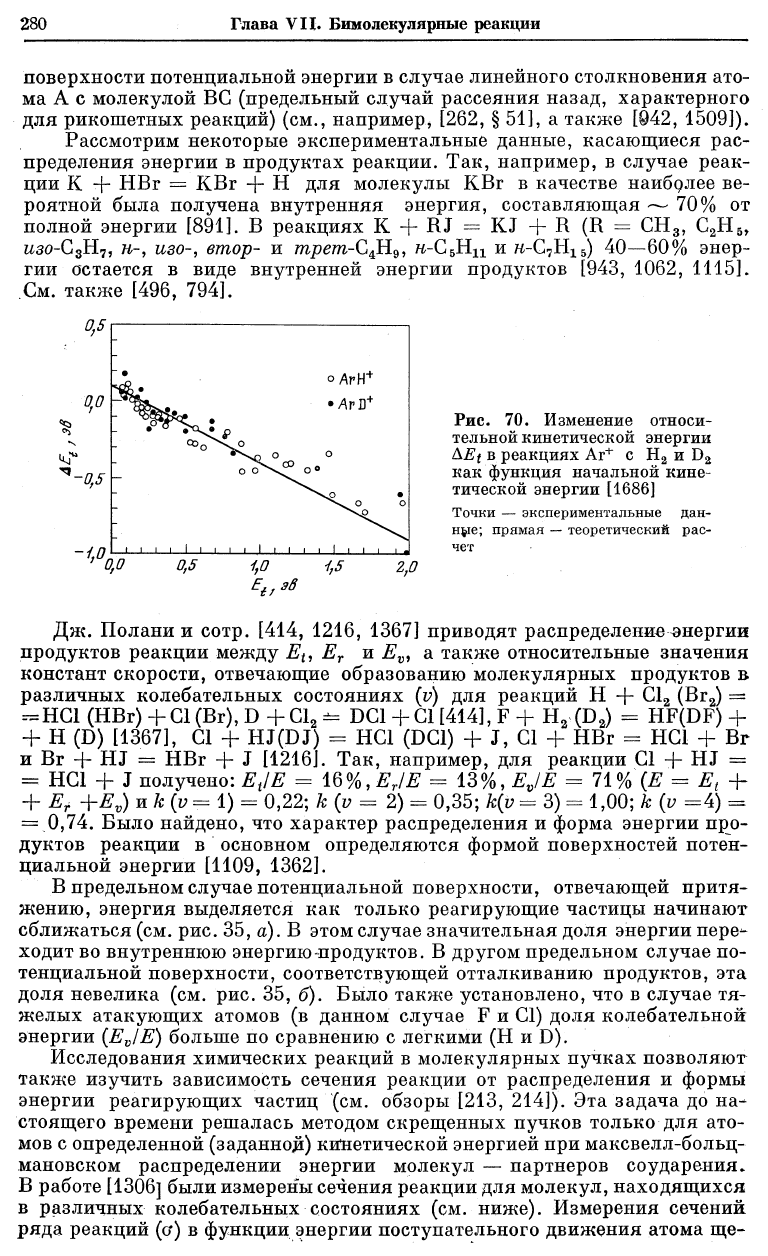
полнительного постоянного члена в правой части (23.19). Рисунок 70 ил-

люстрирует предсказываемую соотношением (23.18) линейную зависимость

от E

для реакций

Ar+ + Н

—

АгН

+ Н,

Аг

+ — ArD+ + D.

Для рикошетных реакций некоторые представления о распределении

энергии можно получить при исследовании движения тяжелой точки по

поверхности потенциальной энергии в случае линеиного столкновения ато-

ма А с молекулой ВС (предельный случай рассеяния назад, характерного

для рикошетных реакций) (см., например, [262, § 51], а также [042, 1509]).

Рассмотрим некоторые экспериментальные данные, касающиеся рас-

пределения энергии в продуктах реакции. Так, например, в случае реак-

ции К + НВг = КВг + Н для молекулы КВг в качестве наибрлее ве-

роятной была получена внутренняя энергия, составляющая — 70% от

полной энергии [891]. В реакциях К + RJ = KJ + R (R = СН

, С

изо-С

, н-, изо-, втор- и mpem-CJI

, w-C

и и-С

) 40—60% энер-

гии остается в виде внутренней энергии продуктов [943,1062,1115].

См. также [496, 794].

Рис. 70. Изменение относи-

тельной кинетической энергии

AEf в реакциях Аг

с Н

и D

как функция начальной кине-

тической энергии [1686]

Точки — экспериментальные дан-

ное; прямая — теоретический рас-

чет

Дж. Полани и сотр. [414, 1216, 1367] приводят распределение энергии

продуктов реакции между Е

и E

а также относительные значения

констант скорости, отвечающие образованию молекулярных продуктов в

различных колебательных состояниях (v) для реакций Н + С1

(Вг

) =

НС1

(HBr)+Cl(Br),D +С1

±= DC1 + C1[414],F+H

) = HF(DF)+

+ Н (D) [1367], CI + HJ(DJ) = HC1 (DC1) + J, CI + НВг = HC1 + Br

и Br + HJ = HBr + J [1216]. Так, например, для реакции CI + HJ =

= HC1 + J получено: EJE = 16%,E

/E = 13%, EJE = 71%(E = E

+ E+ +E

) и к (v = 1) = 0,22; к (и = 2) = 0,35; k(v = 3) = 1,00; к (и =4) =

= 0,74. Было найдено, что характер распределения и форма энергии про-

дуктов реакции в основном определяются формой поверхностей потен-

циальной энергии [1109, 1362].

В предельном случае потенциальной поверхности, отвечающей притя-

жению, энергия выделяется как только реагирующие частицы начинают

сближаться (см. рис. 35, а). В этом случае значительная доля энергии пере-

ходит во внутреннюю энергию-продуктов. В другом предельном случае по-

тенциальной поверхности, соответствующей отталкиванию продуктов, эта

доля невелика (см. рис. 35, б). Было также установлено, что в случае тя-

желых атакующих атомов (в данном случае F и С1) доля колебательной

энергии (E

/E) больше по сравнению с легкими (Н и D).

Исследования химических реакций в молекулярных пучках позволяют

также изучить зависимость сечения реакции от распределения и формы

энергии реагирующих частиц (см. обзоры [213, 214]). Эта задача до на-

стоящего времени решалась методом скрещенных пучков только для ато-

мов с определенной (заданнод) кинетической энергией при максвелл-больц-

мановском распределении энергии молекул — партнеров соударения.

В работе [1306] были измерены сечения реакции для молекул, находящихся

в различных колебательных состояниях (см. ниже). Измерения сечений

ряда реакций (а) в функции энергии поступательного движения атома ще-