Комаров Ю.Ю. Проектирование и изготовление аэрокосмических аппаратов

Подождите немного. Документ загружается.

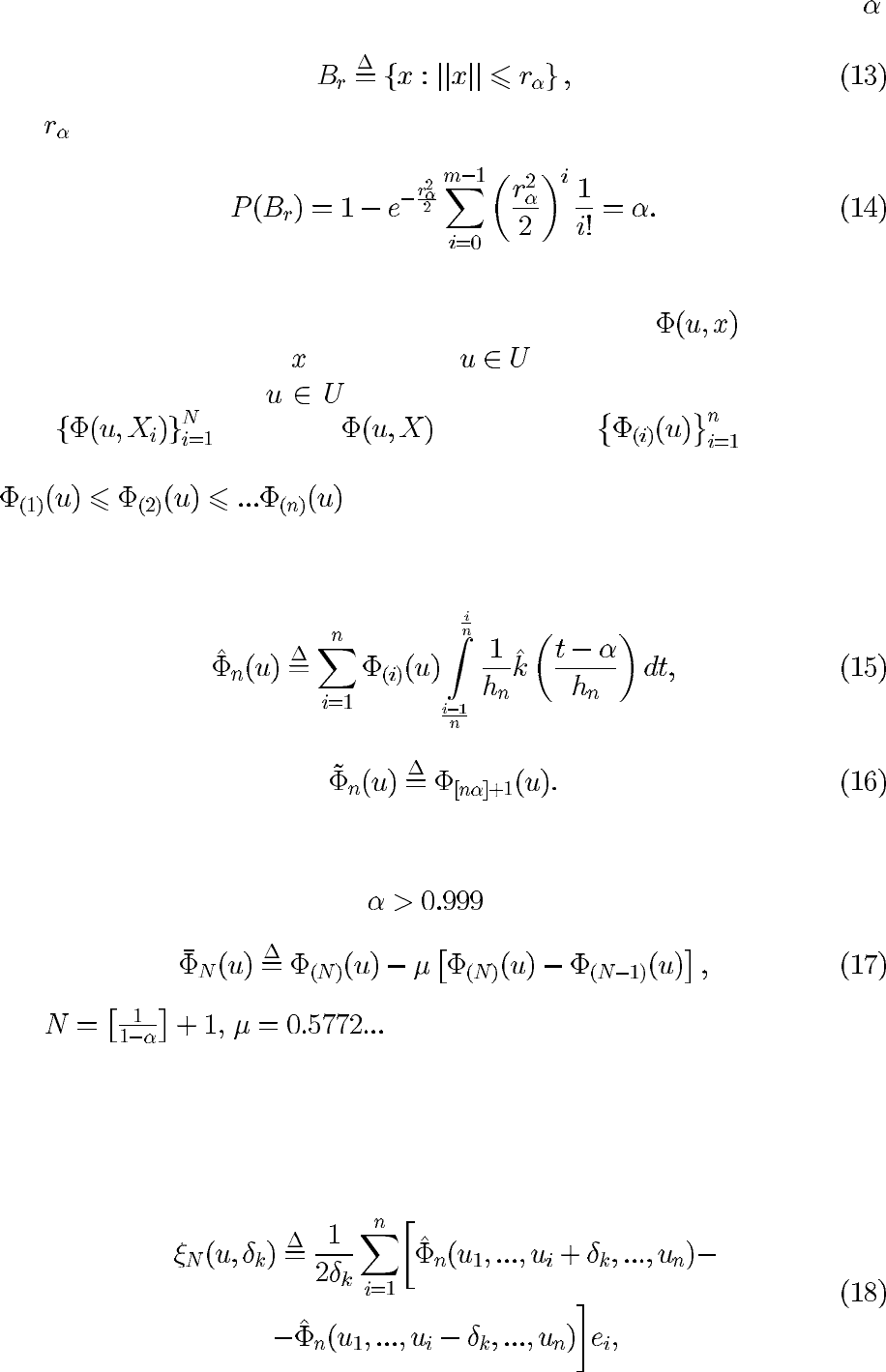
Обычно в качестве доверительного множества выбирается шар меры ,

т.е.

где определяется из следующего уравнения [8]:

Однако стоит заметить что применение стандартных численных мето-

дов решения задачи (12) затруднено тем, что функция

может быть

многоэкстремальной по

для любого .

Пусть для любого

есть возможность получить выборку значе-

ний

функции . Обозначим — вариаци-

онный ряд выборки, т. е. расположенные в порядке возрастания значения

На основе данного вариационного ряда сконструируем ядерную оценку

типа (2). Положим

В работе [7] предложена эффективная оценка функции квантили в слу-

чае нормального распределения средних членов вариационного ряда для

высоких уровней вероятности

где - константа Эйлера.

Оценка (15) удобна для применения в стохастических квазиградиентных

процедурах, когда значение квантили необходимо оценивать многократ-

но при различных значениях аргумента. Введем некоторые определения.

Назовем стохастическим квазиградиентом функции квантили случайный

вектор

281

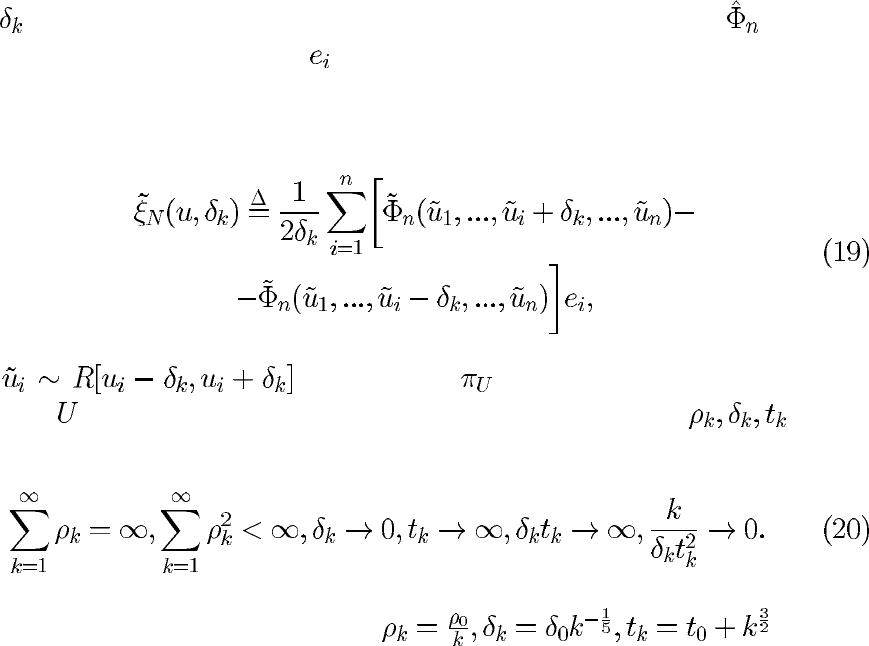
где — детерминированная убывающая последовательность; — стати-

стическая оценка типа (15);

— единичные орты координат. Так как вы-

борочная оценка (16) функции квантили не является дифференцируемой,

то для нее рассматривается сглаженный стохастический квазиградиент

где . Обозначим — оператор проецирования на

область

, и пусть существуют такие последовательности такие,

что

Например, последовательность удовле-

творяет ограничениям (20).

Библиографический список

1. Kibzun A. I., Kan Yu. S. Stochastic programming problems (with probability and quantile

functions). – London: J. Willey & Sons, 1996.

2. Дэйвид Г. Порядковые статистики. – М.: Наука, 1979.

3. Галамбош Я. Асимптотическая теория экстремальных порядковых статистик. – М.:

Наука, 1984.

4. Parzen E. Nonparametric Statistical Data Modeling //Journal of the American Statistical

Association. 1979. Vol. 74. №365. С. 105-131.

5. Falk M. Relative of kernel type estimators of quantiles// Universitat-Gesamthochschule

Siegen. 1983. Vol. 12. №1. C. 261-267.

6. Tamm E. Estimation of quantiles avoding order statistics//Research Report Math. 55/92.

Institute of Cybernetics, Estonian Academy of Sciences, 1992.

7. Кибзун А. И., Курбаковский В. Ю. Численные алгоритмы квантильной оптимиза-

ции и их применение к решению задач с вероятностными ограничениями// Изд.

АНСССР. Техническая кибернетика. 1991. №1. C. 75-81.

8. Малышев В. В., Кибзун А. И. Анализ и синтез высокоточного управления летатель-

ными аппаратами. – М.: Машиностроение, 1987.

9. Пугачев В. С. Лекции по функциональному анализу. – М.: Изд-во МАИ, 1996.

282

О. А. Москаленко

Московский авиационный институт (государственный технический университет)

ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ ЦИФРОВЫХ СИСТЕМ

ВИДЕОНАБЛЮДЕНИЯ И ВИДЕОВЕЩАНИЯ ДЛЯ БЮДЖЕТНЫХ

УЧЕБНЫХ ОРГАНИЗАЦИЙ

В последнее время одной из самых актуальных задач, решаемых в каж-

дой организации, такой, как вуз, банк, магазин или административное зда-

ние, является обеспечение безопасности.

Одной из главных составляющих системы безопасности является си-

стема видеонаблюдения.

Современные комплексы видеонаблюдения подчас недоступны для бюд-

жетных организаций. Хотелось бы организовать компьютерную систему

видеонаблюдения в лабораторных классах, позволяющую:

1. С любого компьютера в сети наблюдать за происходящим в помеще-

нии.

2. Хранить всю записанную информацию в течение определенного вре-

мени.

3. Начинать запись по расписанию или в случае обнаружения движения

(шума).

4. Сжимать получаемую информацию для экономии места на диске

компьютера.

5. Опубликовывать видеофайлы на сервере.

6. Обеспечивать расширяемость, т. е. возможность подключения допол-

нительных камер.

В данной статье мы дадим рекомендации для создания такой системы

видеонаблюдения, которая решала бы все поставленные задачи, а затраты

на ее создание были бы минимальны.

1. Основные типы систем видеонаблюдения

Существуют четыре основных типа систем видеонаблюдения:

Цифровая система.

Аналоговая система.

Система на основе сетевых решений.

Интегрированная система видеонаблюдения.

283

Далее остановимся на рассмотрении цифровых систем.

Цифровая система видеонаблюдения имеет гораздо больше плюсов, чем

аналоговая, а именно: отсутствие необходимости менять видеокассеты;

удобный поиск информации; возможность распечатать нужный кадр; воз-

можность быстро сохранить необходимый фрагмент видеозаписи; наличие

фильтров для обработки изображения; высокое качество видеоинформа-

ции; работа по расписанию; встроенный детектор движения; возможность

работы с телеметрией; возможность подключения охранных датчиков; ра-

бота в компьютерной сети как локальной, такивсетиИнтернет.

Компьютерная система видеонаблюдения состоит из следующих ком-

понентов:

Системный блок персонального компьютера. Как правило, это ком-

пьютер с мощным процессором, видеокартой, жестким диском боль-

шого объема.

Платы видеозахвата. Позволяют принимать аналоговый сигнал, по-

ступающий с видеокамер, обрабатывать его и передавать программ-

ному обеспечению для управления им.

Программное обеспечение. Управляет полученным от платы видео-

захвата изображением. В зависимости от настроек и возможностей

конкретной системы может записывать видеоинформацию, архивиро-

вать, осуществлять поиск и т.д.

Камера.

Рассмотрим схемы организации системы видеонаблюдения на основе

FireWire камеры, Web-камеры и IP (сетевой) камеры. FireWire камеры

(рис. 1) можно подключить к компьютеру через порт IEEE 1394 (FireWire).

Рис. 1. FireWire камера

284

IEEE 1394 (FireWire) — последовательная высокоскоростная шина, пред-

назначенная для обмена цифровой информацией между компьютером и

другими электронными устройствами — он есть в каждой цифровой ка-

мере. Изменяемая архитектура и одноранговая топология шины дела-

ют FireWare идеальным вариантом для подключения жестких дисков и

устройств обработки аудио- и видеоинформации. Эта шина также идеально

подходит для работы мультимедийных приложений в реальном времени.

Web-камеры (рис. 2) — это будущее охранных систем. Пока что Web-

камеры можно применять для обзорных целей, но не для охранных. Для

выполнения охранной функции им не хватает качества изображения (чет-

кости и резкости из-за необходимости сильного сжатия информации), ско-

рости передачи данных, а также надежности (из-за отсутствия средств под-

тверждения пакета событие просто может быть пропущено). Технологии

обзорно-охранных Web-камер бурно развиваются.

Рис. 2. Web-камера Genius VideoCAM Express

Сетевая (IP) камера. Современная сетевая камера представляет собой

цифровое устройство, производящее видеосъемку, оцифровку, сжатие и пе-

редачу по компьютерной сети видеоизображения. В состав сетевой камеры

входят: ПЗС-матрица; объектив; оптический фильтр; плата видеозахвата;

блок компрессии (сжатия) видеоизображения; центральный процессор и

встроенный web-сервер; ОЗУ; флэш-память; сетевой интерфейс; последо-

вательные порты; тревожные входы/выходы. Каждая сетевая видеокамера

имеет свой собственный IP-адрес, вычислительные функции и встроенное

программное обеспечение, что позволяет ей функционировать как web-

сервер, FTP-сервер, FTP-клиент и клиент e-mail. Наиболее современные

сетевые видеокамеры включают и много других привлекательных функ-

ций, таких, как детектор движения, вход/выход тревоги и поддержка e-

mail.

Со встроенным web-сервером, для передачи полученного изображения

285

по сети, сетевая камера не нуждается в прямом подключении к компьютеру

или любым другим аппаратным или программному средствам.

Таблица

Сравнительная таблица сетевой камеры

и камеры на основе PC

Сетевая камера Камера на основе PC

Гибкость Размещая камеру где угодно,

можно подключить ее к се-

ти с помощью модема, сото-

вого телефона или беспровод-

ного адаптера

Прикрепленная PC камера

должна быть в пределах трех

метров от компьютера

Функциональные

возможности

Все видео оперативно переда-

ется по сети без каких-либо

задержек и дополнительного

оборудования

Помимо камеры, всегда необ-

ходим компьютер и программ-

ное обеспечение

Инсталляция Надо установить только IP-

адрес, и камера готова к ра-

боте

Инсталляция драйверов и про-

граммного обеспечения на PC

усложнена

Простота в ис-

пользовании

Можно управлять и рассмат-

ривать изображения, исполь-

зуя стандартный Web-браузер

на любом PC

Необходимо определенное

программное обеспечение.

Отсутствует возможность

в удаленном администрирова-

нии

Стабильность Камера работает без лю-

бых дополнительных компо-

нентов, давая большую ста-

бильность

Стабильность работы зави-

сит от стабильности ком-

пьютера, а также от про-

граммного обеспечения

Качество Высокое качество при исполь-

зование MPEG

Используются компоненты

невысокого качества, отсюда

небольшое разрешение

Стоимость Стоимость сетевой камеры

— это только стоимость се-

тевой камеры

Стоимость решения = общая

стоимость камеры + компью-

тер + программное обеспече-

ние

2. Реализация системы видеонаблюдения

Система на основе IP (сетевой) камеры. Для реализации системы

видеонаблюдения в компьютерном классе были использованы интернет

камера-сервер TV-IP200 и программа IP-view. Камера изображена на рис. 3.

Интернет камера-сервер TV-IP200 - это устройство для удаленного мо-

ниторинга и передачи событий в реальном времени через локальную сеть

или Интернет. Устройство имеет высокую надежность, возможность ин-

теграции в сети Fast Ethernet, а также обеспечивает возможности видео-

наблюдения в реальном времени через web-браузер по Интернет или Ин-

транет. Камера TV-IP200 является идеальным устройством для ведения

286

Рис. 3. Камера-сервер TV-IP200 и программа IP-view

широковещательных видеопередач через Интернет, обеспечивает съемку

видеокачества VGA, возможность автоматической съемки, извещение о

событиях через электронную почту, а также имеет дополнительные разъ-

емы ввода/вывода.

Первоначально не удалось найти ни возможности просмотра несколь-

ких камер одновременно, ни способы настроек датчика движения. После

установки программы IP-View все стало на свои места. Эта программа

позволяет подключать до 64 камер (по IP-адресу), обеспечивает возмож-

ность просмотра 1, 4, 9 или 16 камер одновременно на одном экране,

возможность настройки параметров записи видео на жесткий диск, а так-

же параметров отправки стоп-кадров на FTP-сервер или на электронный

адрес для каждой камеры.

На последнем пункте остановимся более подробно. Запись на винчестер

может производиться как постоянно, так и по расписанию и при срабаты-

вании датчика движения. В первом режиме запись ведется циклично; при

достижении avi-файлом заданного размера или продолжительности наибо-

лее старые данные начинают замещаться новыми. По расписанию запись

может вестись в определенные дни недели и в определенное время. По сра-

батыванию датчика движения в поле зрения камеры запись прекращается

через 10 секунд после прекращения движения.

Такой режим очень рационален: зачем снимать пустующую аудиторию

в выходной день и забивать жесткий диск неподвижной картинкой? Чув-

ствительность датчика выставляется в соответствующем меню программы

IP-View при помощи “ползунка” с несколько абстрактными min, max и

какими-то промежуточными значениями. При максимальных параметрах

287

чувствительности камера реагирует и производит съемку попавших в поле

ее зрения мелких частиц.

Кстати, при средней степени сжатия и среднем качестве изображения

(320х240) полутораминутная запись, вызванная срабатыванием датчика

движения, заняла на жестком диске всего 280 Кб.

Система на основе Web и FireWire камер создана на основе камер,

подключаемых к компьютеру, программы WebCam Monitor, предназначен-

ной для построения простейшей следящей системы. Монитор имеет два

режима слежения: непрерывный/периодический и фиксации движения. В

первом режиме запись изображения идет постоянно или кадрами через

заданный промежуток времени, а результаты размещаются на диске или

отправляются по сети на FTP-сервер. Во втором режиме задается степень

чувствительности к изменению деталей изображения (движению объектов

в поле зрения) и действие, выполняемое при изменении изображения сверх

минимально допустимого за единицу времени. Анализу может подвергать-

ся не все изображение, а отдельно указанная прямоугольная область. При

срабатывании детектора монитор может воспроизвести заданный звуковой

файл, привлекая внимание тех, кто находится рядом, отправить снимок

на FTP-сервер, либо отправить почтовое сообщение (e-mail) по заданному

адресу.

Результаты практических испытаний

Рассматриваемая система строилась по результатам анализа следующих

потребностей:

Система использует имеющуюся в наличии сетевую камеру и допус-

кает расширение до 16 камер.

Съемка производится каждый день при наличии движения в лабора-

торном классе.

Вся информация с камеры хранится на сервере и удаляется через

определенное время.

Возможность просмотра как архивов, так и текущей оперативной об-

становки в масштабе реального времени, не нарушая при этом процесс

записи видеоархива.

Камера устанавливается напротив двери в лабораторный класс.

Были протестированы многие программы для разных типов камер, но

самыми подходящими оказались две программы: IP-View (для сетевой ка-

меры) и WebCam Monitor (для Web и FireWire камер).

288

Программа IP-View имеет недостатки, основным из них является невоз-

можность запуска ее как сервиса, так как при запуске программа требу-

ет ввести данные для аутентификации, причем не используются средства

аутентификации MS Windows; к недостаткам относится также невозмож-

ность удаления видеоархивов.

Недостатком WebCam Monitor является медленное и прерывистое ве-

щание видеопотока по сети.

В данной статье были рассмотрены три модели:

На основе IP (сетевой) камеры.

На основе Web-камеры.

На основе FireWire-камеры.

Удобной в использовании оказалась сетевая камера. Web и FireWire

камеры дают плохое изображение.

Построенная система на базе IP (сетевой) камеры полностью удовле-

творяет все вышеперечисленные требования.

Библиографический список

1. Магауенов Р. Г. Системы охранной сигнализации: основы теории и принципы по-

строения: Учебное пособие. – М.: Горячая линия-Телекомф, 2004.

2. Гарсия М. Проектирование и оценка систем физической безопасности / Пер. с англ.;

Под ред. Р. Г. Магауенова. – М.: Мир, 2002.

3. Волхонский В. В. Телевизионные системы наблюдения. – Спб.: Экополис и культура,

1997.

4. Проектирование систем видеонаблюдения и видеоконтроля. – Спб.: Ультра-Стар,

1996.

5. Омельянчук A. M. Применение видеотехники в охране. – М.: ТВ «Безопасность»,

1995.

6. Системы охранного телевизионного наблюдения. – М.: НИЦ ТВ «Охрана», 1997.

7. Таненбаум Э. Современные операционные системы. 2-е изд. – Спб.: Питер, 2002.

В. В. Василевский, И. О. Кульшенко, Е. Л. Матвеев, А. В. Сидоркин

Московский авиационный институт (государственный технический университет)

СТОХАСТИЧЕСКАЯ МОДЕЛЬ РАСПОЗНАВАНИЯ ОБРАЗОВ,

ИНВАРИАНТНАЯ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЙ

КООРДИНАТ

В связи с активным использованием информационных технологий при

289

решении задач автоматизации человеческой деятельности большую роль

играют интеллектуальные методы распознавания изображений, лежащие в

основе современных систем машинного зрения.

Одной из важных проблем теории распознавания образов является зада-

ча классификации, которая заключается в разбиении множества объектов

на классы (категории) по определенному критерию. Объекты в пределах

одного класса считаются эквивалентными. Примерами задач классифика-

ции могут служить: распознавание текста, распознавание речи, идентифи-

кация личности.

Авторами предлагается обучаемая стохастическая многокритериальная

модель классификации и распознавания образов на основе их числовых

характеристик.

Для применения математических методов решения задачи классифика-

ции необходимо измерение геометрических характеристик объекта, что, в

свою очередь, требует наличия векторного представления изображения в

памяти компьютера.

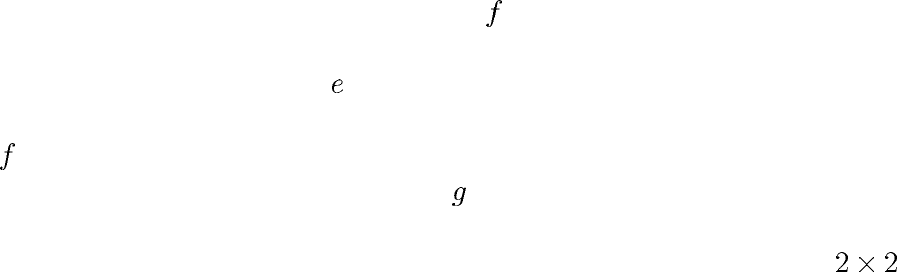
Для векторизации изображения и выделения контуров применяется сле-

дующая схема: исходное изображение

подвергается линейной обработ-

ке, с тем, чтобы выделить перепады яркости. В результате этой операции

формируется изображение

, функция яркости которого существенно отли-

чается от нуля только в областях резких изменений яркости изображения

. Затем в результате пороговой обработки из изображения e формируется

графический (контурный) препарат

. Для выделения перепадов яркости

используется градиентный метод, который в свою очередь сводится к вы-

полнению нелинейной локальной обработки изображения “окном”

Основными параметрами любой плоской фигуры являются ее площадь

и центр масс, а также такие величины, как отношение площади образа к

площади описанной окружности и соотношение площадей сегментов фи-

гуры, а именно отношение верхней половины к нижней и левой к правой

относительно продольной объекта. Для решения задачи построения опи-

сывающей окружности минимального радиуса был применен итеративный

алгоритм, заключающийся в последовательном приближении к интересую-

щей окружности путем построения промежуточных каркасов на заданном

подмножестве вершин и проверки его для оставшихся точек.

Задача нахождения центра масс плоской фигуры в общем случае не яв-

ляется тривиальной. Для поиска этой характеристики проводится триангу-

ляция многоугольника, т.е. декомпозиция на треугольники. Фигура скорее

всего представляет не выпуклый многоугольник, и это усложняет задачу.

Для решения задачи был применен метод “Отсекания углов”, состоящий

290