Комаров Ю.Ю. Проектирование и изготовление аэрокосмических аппаратов

Подождите немного. Документ загружается.

А. В. Крижановский, А. М. Марасанов

Московский авиационный институт (государственный технический университет)

МЕТОДЫ И ПРОГРАММНЫЕ СРЕДСТВА ОБНАРУЖЕНИЯ

И ПРЕДОТВРАЩЕНИЯ СЕТЕВЫХ АТАК НА ОСНОВЕ

“ОПАСНОЙ” ТЕОРИИ ИСКУССТВЕННОГО ИММУНИТЕТА

Сигнатурные системы обнаружения атак имеют ряд недостатков, таких,

как низкая инвариантность обнаруживаемых атак и подверженность ата-

кам, приводящим к большому числу ложных срабатываний. Адаптивные

системы обнаружения атак работают на принципе эквивалентности по-

нятий “аномальность” и “опасность”, что не всегда верно. В этой статье

описывается прототип системы, при разработке которого была предпри-

нята попытка избавиться от вышеуказанных недостатков при сохранении

преимуществ адаптивного и сигнатурного принципов к обнаружению и

предотвращению атак. Особенностью описываемого прототипа также яв-

ляется попытка корреляции результатов анализа сетевого трафика и состо-

яний системных процессов.

Задачей систем обнаружения или предотвращения атак является опреде-

ление событий безопасности, которые могут привести к реализации угро-

зы компрометации информационной системы. Подобную задачу с успехом

решает иммунная система человека.

В классической иммунологии полагается, что иммунный ответ генери-

руется на “чужие” антигены. Такой подход рождает ряд вопросов, напри-

мер, почему у нас в кишечнике живут бактерии, попадающие в нас вместе

с едой? Попыткой объяснить эти вещи стала “Опасная” Теория (Danger

Theory, DT) иммунологии, предложенная Полли Матзингер [1]. Основой

данной теории является предположение о том, что иммунная система на са-

мом деле отделяет некоторые “свои” антигены от некоторых “чужих” и им-

мунный ответ генерируется не на “чужие” антигены, а на опасные [1, 2, 3].

В этой теории опасность измеряется степенью разрушения (стресса) клет-

ки. Когда клетка умирает неестественной смертью (некроз), она посылает

нулевой опасный сигнал. DT предлагает следующий сценарий иммунного

ответа. Клетка, испытывающая стресс, посылает сигнал, после чего анти-

ген, находящийся вблизи, захватывается антигенпрезентирующей клеткой

(APC). Далее APC посылает первый опасный сигнал распознавания, кото-

рый перехватывается T-хелперным лимфоцитом. T-хелперный лимфоцит

может подтвердить “опасность” антигена, представленного APC, посыл-

кой второго опасного сигнала стимуляции. Этот сигнал перехватывается

271

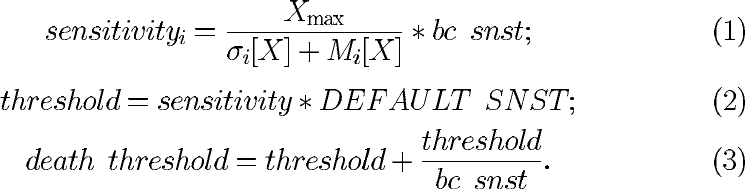
T-киллерным лимфоцитом, который способен непосредственно ликвидиро-

вать зараженную вирусом клетку и может препятствовать проникновению

вируса в соседние клетки. Вводится понятие опасной зоны – некоторой

области рядом с источником сигнала, в которой B-лимфоциты (один из

видов APC) генерируют антитела, соответствующие антигенам, попавшим

в эту зону. При генерации антител для антигенов из опасной знаы запуска-

ется процесс клональной селекции, обеспечивающий генерацию наиболее

подходящих антител.

По аналогии с DT можно провести связь между биологической клеткой

и парой сокет-процесс для ОС. Эта пара подобно биологической клет-

ке способна делиться (группы системных вызовов fork() и accept()), для

нее легко определить стресс (обращение к “необычным” файлам, аномаль-

ное отношение использования системных ресурсов к интенсивности об-

рабатываемых сетевых запросов, десинхронизация TCP сеансов и т.д.). В

нормальном режиме работы системы для уменьшения числа ложных сра-

батываний сначала исследуется поведение процесса и при сильном его

отклонении от “нормы” исследуется трафик в соответствии с сигнатурами

(стоит вспомнить утилиту Snot, способную “заваливать” Snort’а огромным

количеством ложных атак). Сигнатурный анализ производится T-хелпером.

На самом деле сетевой трафик и поведение процесса исследуются парал-

лельно, но при нахождении соответствия сигнатуре при нормальном пове-

дении процесса никаких действий принято не будет. Однако на этапе кон-

фигурации пользователь может отдельно задать сигнатуры, которые могут

независимо от состояния процесса генерировать тревогу. Таким образом,

получаем систему дух сигналов: распознавания и стимуляции.

Анализ производится по таким параметрам, как обращение к файлам,

отношение сетевых запросов серверному процессу к откликам, использо-

вание системных ресурсов и т.д. При конфигурации системы можно задать

приблизительные значения (они могут изменяться с ограниченной скоро-

стью при обучении системы) вышеуказанных параметров,ивэтомслучае

система сможет обнаруживать атаки, производимые злоумышленниками на

стадии обучения. При обучении вырабатываются два пороговых значения

для отклонений от “нормального” поведения процесса, а также чувстви-

тельности для каждого из параметров (или веса параметров):

272

Здесь – значение исследуемого параметра; – матожидание зна-

чения параметра;

– среднеквадратическое отклонение. Эти значения

вычисляются рекуррентно по следующим формулам (так как система ре-

ализована в ядре ОС, то все вычисления являются целочисленными):

Здесь tot_t – суммарное время от начала измерений до предыдущего

измерения включительно;

– среднее время, за которое было получено

текущее значение

; bc_snst – чувствительность B-клетки (анализатора

состояния процесса).

В рабочем режиме система изменяет значение стресса клетки в соот-

ветствии с взвешенными суммами отклонений на основе чувствительности

параметров системного процесса следующим образом:

При превышении значением стресса клетки первого порога исследуют-

ся результаты сигнатурного анализа сетевого трафика. При превышении

второго порога (смертельного порога, death_threshold) запускается меха-

низм клональной селекции для поиска новых сигнатур сетевых атак в

полученном процессом сетевом трафике.

Этот механизм работает следующим образом. Для процесса определя-

ется опасная зона как последовательность сетевых запросов прикладного

уровня (реализовано в виде кольцевого буфера). При пересечении уровнем

стресса клетки первого порога все запросы, на которые не был отправ-

лен ответ, делятся на

частей, и эти части далее ищутся в нормальном

трафике для данного процесса (вернее, всех процессов для данного ис-

полняемого файла). Части, которые были найдены, выбывают. Оставшие-

ся части опять делятся на

частей, и процедура повторяется. Значения

определяются в зависимости от текущего числа искомых частей сооб-

щений. Эта процедура повторяется конфигурируемое число раз, после чего

результаты предъявляются офицеру безопасности для анализа. При отсут-

ствии реакции от офицера безопасности генерируются регулярные выра-

жения из оставшихся частей сообщений и добавляются в сигнатурную базу

T-хелпера. Поскольку такие сигнатуры обладают сравнительно низким ка-

чеством, они могут выступать только как данные для “подтверждающего”

анализа.

273

Система реализуется на уровне ядра ОС, что дает ей возможность рабо-

тать в реальном масштабе времени и предпринимать активные действия по

предотвращению атак путем возвращения ошибок из системных вызовов

и блокирования сетевого трафика, читаемого процессом.

Библиографический список

1. Plloy Matzinger. The real function of the immune system or tolerance and the four D’s

(danger, death, destruction and distress).

http://cmmg.biosci.wayne.edu/asg/polly.html.

2. Uwe Aickelin, Steve Cayzer. The Danger Theory and its application to artiﬁcial immune

systems // 1st International Conference on AIS, 2002.

3. Uwe Aickelin, Peter Bentley, Steve Cayzer, Jung Won Kim, Julie McLeod. Danger

Theory: the link between AIS and IDS? // Digital Media Systems Laboratory. – Hewlett-

Packard, 2003.

4. Jung Won Kim, Peter J. Bentley. Towards an artiﬁcial immune system for network

intrusion detection: an investigation of dynamic clonal selection // The Congress on

Evolutionary Computation (CEC), 2002.

Г. Н. Кузьмин, С. А. Фатеев, А. А. Пунтус

Московский авиационный институт (государственный технический университет)

МЕТОДИКА ДИСТАНЦИОННОГО ОБУЧЕНИЯ РЕШЕНИЮ

ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Дифференциальные уравнения применяются для описания и исследо-

вания многих задач в науке и технике: физике, механике и т.п. Сейчас

активно разрабатываются и широко применяются численные методы ре-

шения дифференциальных уравнений, как одних из важнейших объектов

изучения и исследования современной науки. Поэтому их изучение обя-

зательно для дипломированного специалиста математических, физических

и инженерных специальностей. Курс “Обыкновенные дифференциальные

уравнения” является важным прикладным курсом для этих специалистов.

На его основе построены многие другие важные дисциплины.

Данная работа представляет собой электронный учебник по курсу

“Обыкновенные дифференциальные уравнения”, удовлетворяющий основ-

ным требованиям к дистанционным обучающим программам. В нем пред-

ставлена первая часть курса, посвященная аналитическим методам реше-

ния задач Коши для обыкновенных дифференциальных уравнений, то есть

методы поиска решений дифференциальных уравнений в квадратурах.

274

Этот электронный учебник может быть использован как в качестве при-

ложения к курсу обыкновенных дифференциальных уравнений, так и в

качестве самостоятельного пособия. В первом случае с помощью данного

учебника можно проводить закрепление материала и проверку его усво-

ения. Тестирование показывает, насколько хорошо обучаемый научился

решать задачи. Не рекомендуется целиком полагаться на результаты тести-

рования при оценке знаний по предмету. Тест должен быть подкреплен

контрольными и расчетно-графическими работами, выполняемыми сту-

дентами самостоятельно, а затем проверяемыми преподавателями. Теоре-

тические знания, такие, как доказательства теорем и утверждений, которе

показывает глубину познаний студента в данном курсе, сложно проверить

с помощью теста. Поэтому настоятельно рекомендуется проводить полно-

ценный экзамен.

Учебник написан на html с использованием javascript. Поэтому, будучи

размещенным в Интернете, доступен на всех компьютерах, подключенных

к глобальной сети, независимо от аппаратной и программной части их со-

ставляющей. Доступность и массовость компьютерной техники позволяет

внедрять данную технологию обучения уже сейчас, без особых затрат, тем

самым упрощая процесс приобретения знаний и обогащая возможность их

получения.

Учебник разбит на главы, по одной на каждый из типов дифферен-

циальных уравнений. Рассмотрены дифференциальные уравнения с раз-

деляющимися переменными, однородные дифференциальные уравнения

первого порядка, линейные уравнения первого порядка и сводящиеся к

ним. Представлена теория линейных дифференциальных уравнений выс-

ших порядков и систем линейных дифференциальных уравнений. Глава

состоит из краткой теоретической справки, подробного алгоритма решения

рассматриваемого типа дифференциального уравнений и примеров, демон-

стрирующих данный алгоритм в действии. После прочтения теоретическо-

го материала программа предложит его закрепить путем тестирования. В

тесте предложен ряд вопросов. В случае неверного ответа задается наво-

дящий вопрос, который может помочь ответу на предыдущий вопрос. Для

задачи на решение дифференциального уравнения существуют несколько

подзадач, разбивающих решение уравнения по пунктам алгоритма на бо-

лее простые части. Таким образом, при тестировании выявляются уровни

подготовки обучаемого, которые не только позволяют судить, умеет или

не умеет он решать задачи, но и выясняют, почему он не решил ту или

иную задачу: например, неправильно определил тип, не усвоил алгоритм,

ошибся в вычислениях и т.д. и т.п. По окончании тестирования выда-

275

ется подробный отчет с оценкой, указанием правильно решенных задач,

неверных ответов и ссылками на раздел курса, прочтение которого может

позволить устранить данный пробел.

Представленное электронное пособие на данный момент уже получило

практическое применение в учебном процессе на одном из факультетов

Московского авиационного института в качестве приложения к курсу ма-

тематического анализа, позволило расширить методы обучения студентов,

повысив тем самым их уровень знаний. Таким образом, была продемон-

стрирована необходимость и эффективность дистанционных методов обу-

чения в практической взаимосвязи со стандартными методами и подтвер-

ждена продуктивность сочетания этих методов.

Развитие дистанционных методов обучения и применение информаци-

онных технологий в процессе изучения основных математических дисци-

плин позволит поднять качество знаний на новый уровень. Такие пособия

помогут студентам научиться решать задачи по данным дисциплинам. Но в

то же время заметим, что углубленное изучение данных курсов возможно

только с использованием стандартных классических курсов и самостоя-

тельной работы студентов с литературой. Но даже и в этом случае элек-

тронный учебник может стать хорошим подспорьем к освоению математи-

ческих дисциплин и, в частности, курса обыкновенных дифференциальных

уравнений.

Библиографический список

1. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1974.

2. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – М.: Регулярная

и хаотическая динамика, 2000.

3. Задачи и упражнения по математическому анализу для ВТУЗов / Под редакцией

Демидовича Б. П. – М.: Наука, 1978.

4. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. – М.:

Наука, 1984.

А. И. Кибзун, Е. Л. Матвеев

Московский авиационный институт (государственный технический университет)

КВАНТИЛЬНАЯ ОПТИМИЗАЦИЯ

НА ОСНОВЕ ЯДЕРНЫХ ОЦЕНОК

Во многих прикладных задачах часто приходится решать оптимизаци-

онные задачи c критерием в форме квантили [1]. В связи с этим актуальной

276

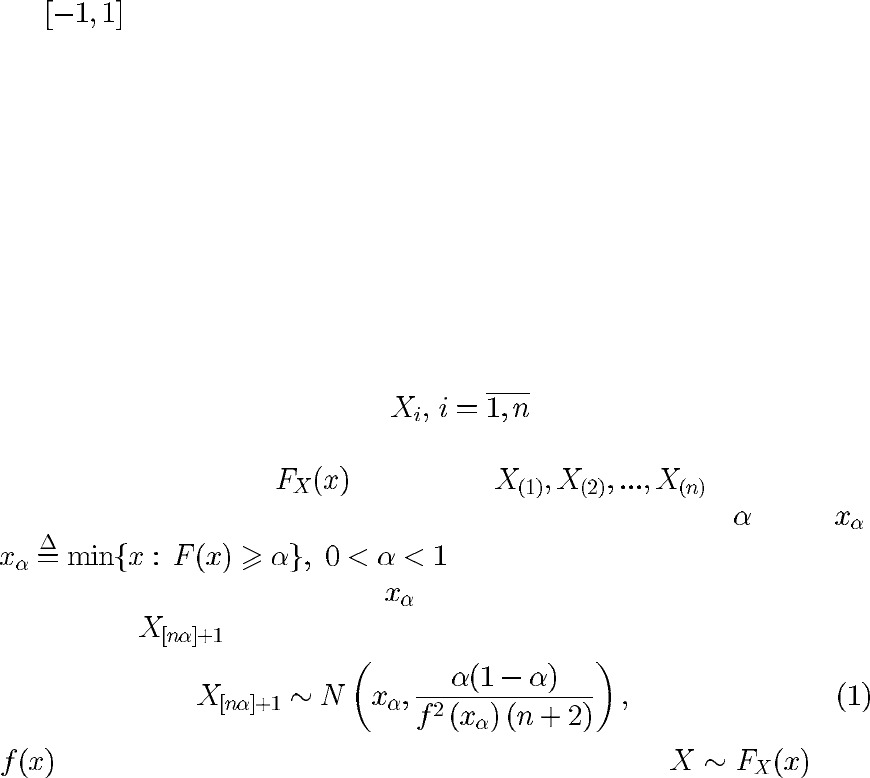
становится проблема построения эффективных алгоритмов оценивания и

оптимизации функции квантили.

Существуют различные виды оценок функции квантили. Самой первой

была выборочная оценка. Ее свойства изучались многими авторами (см.,

например [2], [3]). Однако выборочная оценка была неэффективна при вы-

соких уровнях доверительной вероятности и при оптимизации из-за раз-

рывности ее структуры. Е. Парзеном [4] была предложена ядерная оценка

функции квантили, свободная от этого недостатка. М. Фалк [5] исследовал

асимптотическое поведение первых моментов ядерной оценки квантили.

Данные оценки основаны на использовании порядковых статистик. Аль-

тернативный подход был предложен Е. Таммом [6], который основывается

на решении некоторого функционального уравнения. Упомянутые оценки

были положены в основу алгоритмов квантильной оптимизации, например

в [7] предложен квазиградиентный алгоритм на основе выборочной оценки

функции квантили, с использованием свойств экстремальных порядковых

статистик. Однако данный алгоритм базируется на точном знании закона

распределения выборки, что в прикладных задачах не всегда выполнимо.

В настоящей статье предложено оптимальное в классе финитных функ-

ций на

ядро; исследованы его свойства, а также вычислены асимп-

тотические отклонения ядерной оценки от истинного значения квантили.

Полученная оценка применена для решения задачи стохастического про-

граммирования с оптимизируемым критерием в виде квантили распреде-

ления случайной величины.

В качестве примера рассматривается задача оптимального выбора пара-

метров ВПП (взлетно-посадочной полосы) [7] при заданном ограничении

на безопасность посадки, сводящихся к задаче безусловной квантильной

оптимизации. Показано, что ядерная оценка наиболее универсальна, её

можно применять вне зависимости от величины уровня доверительной

вероятности.

Основные определения. Пусть

- последовательность неза-

висимых, одинаково распределенных величин с абсолютно непрерывной

функцией распределения

. Положим - последова-

тельность порядковых статистик. Обозначим квантиль уровня

через ,

т.е.

Существуют различные оценки

. Наиболее часто используется выбо-

рочная оценка

, так как согласно теореме Мостеллера [2]

где — плотность вероятностей случайной величины .Од-

277

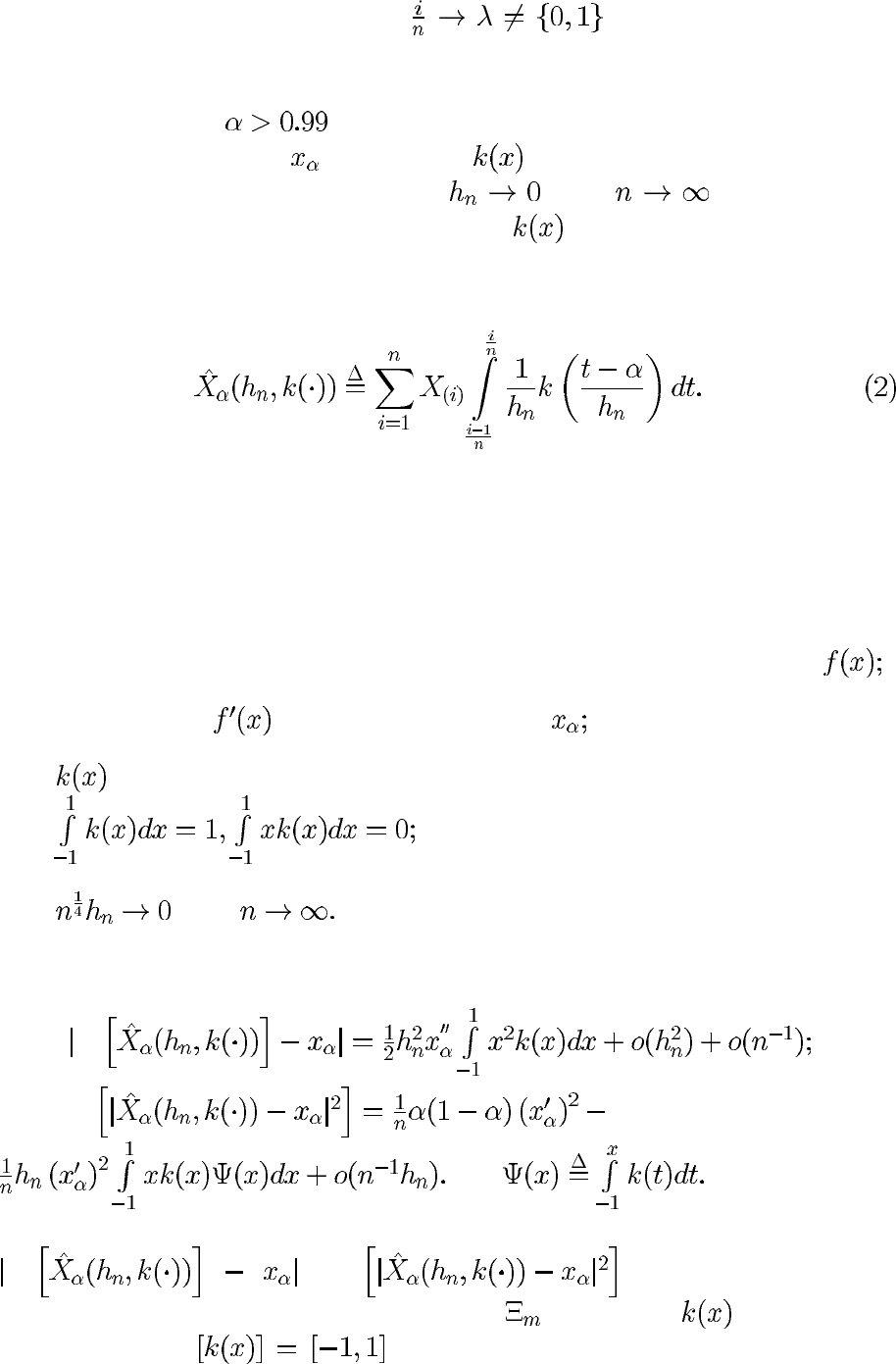
нако это соотношение выполняется только для “средних” членов вариаци-

онного ряда, т. е. для таких, что

. Представляют интерес

квантили для высоких уровней вероятностей, так как в большинстве при-

кладных задач требуется исследование для уровней вероятностей, близких

к единице, т.е. для

. В связи с этим Парзеном [4] была предложена

альтернативная оценка

. Положим, — симметричная относитель-

но нуля плотность распределения и

при . Тогда ядерная

оценка квантили, соответствующая ядру

, определяется следующим

выражением:

Исследуем основные свойства этой оценки.

Теорема 1. Пусть выполнены следующие условия:

1) функция распределения случайной величины имеет плотность

2) существует , непрерывная в точке

3) — финитная плотность вероятностей, такая, что

4) при

Тогда:

А)

Б) M

где

Естественно возникает вопрос о минимизации величин

M иM . Для минимизации

данных выражений сформируем класс

функций с конечным

носителем, supp

определенных на всей числовой прямой

278

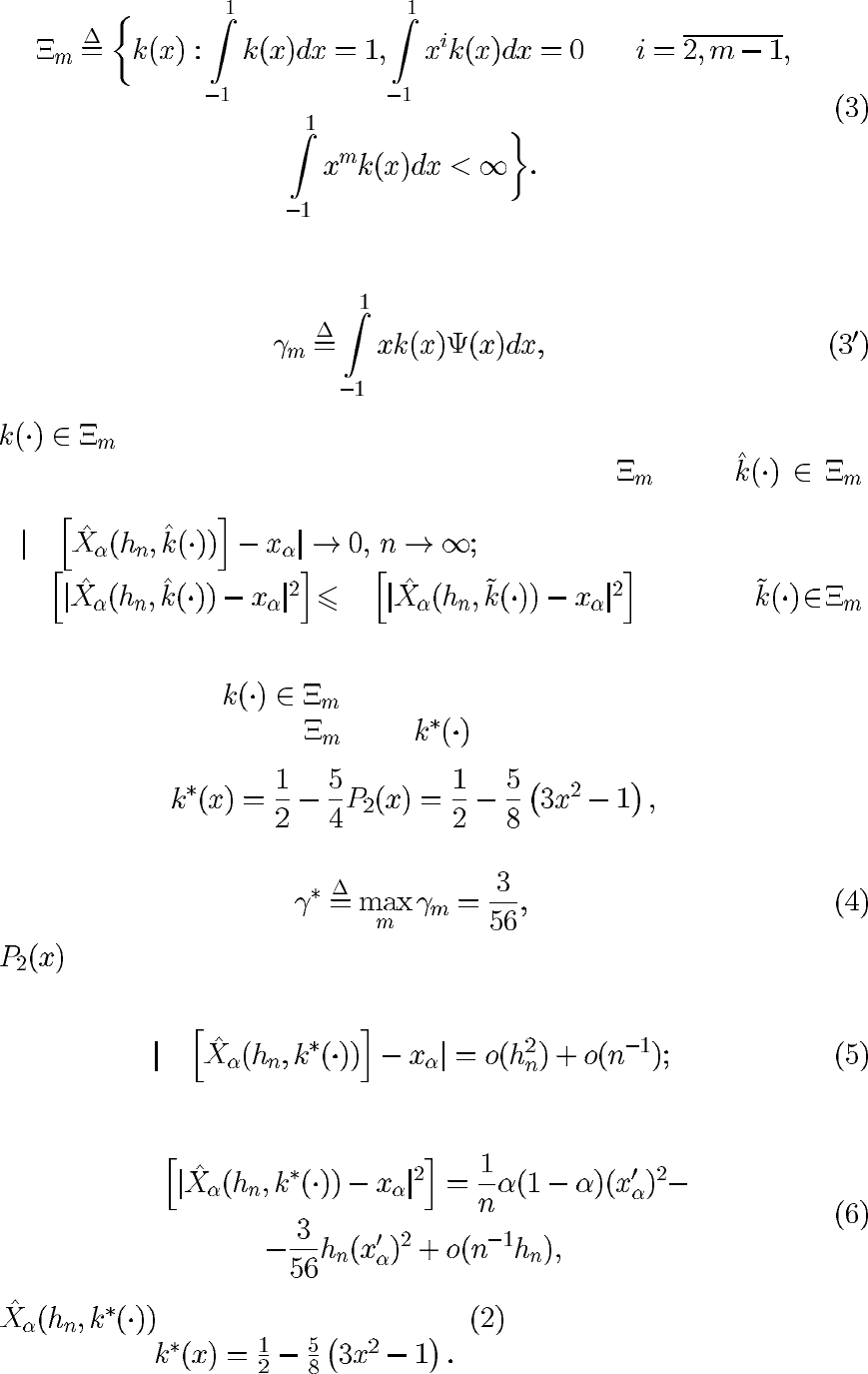
таких, что

для

Введем следующее обозначение:

где .

Определение 1. Назовем оптимальным в классе

ядро ,

если:

1) M

2) M M для всех .

При данных обозначениях справедлива следующая теорема.

Теорема 2. Пусть

. Тогда:

А) оптимальное в классе

ядро будет иметь вид

при этом

где — полином Лежандра 2-й степени;

Б) при этом смещение оценки равно

В) дисперсия оценки определяется соотношением

где — ядерная оценка типа , где в качестве ядра исполь-

зуется функция

279

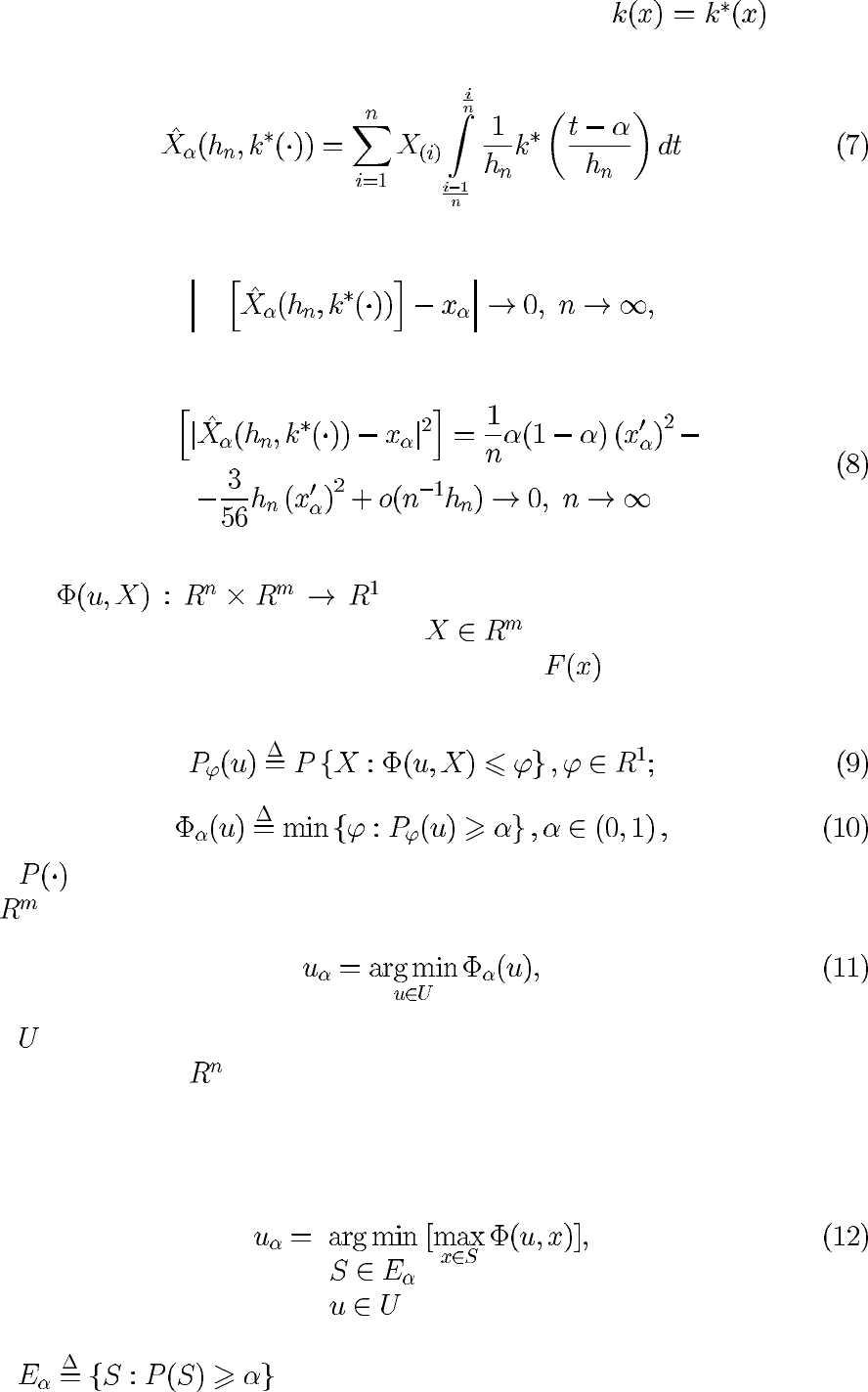
При использовании в качестве ядерной функции получа-

ется, что оценка

является асимптотически несмещенной, т.е.

при этом среднеквадратическая ошибка

Квазиградиентный алгоритм оптимизации функции квантили.

Пусть

— непрерывная по совокупности аргу-

ментов действительная функция, где

— случайный вектор с абсо-

лютно непрерывной функцией распределения

. Определим функции

вероятности и квантили следующим образом:

где — вероятностная мера, определенная на борелевских множествах

из

. Рассмотрим задачу безусловной минимизации функции квантили:

где — множество допустимых решений, которое предполагается выпук-

лым компактом в

. Существуют различные подходы к решению данной

задачи: доверительный [8] и прямой [7].

Доверительный подход основывается на замене исходной задачи мини-

мизации функции квантили следующей задачей:

где — семейство доверительных множеств.

280