Комаров Ю.Ю. Проектирование и изготовление аэрокосмических аппаратов

Подождите немного. Документ загружается.

ки имитационной модели спутниковой системы космического мони-

торинга земной поверхности.

2. Рассмотрены варианты модели функционирования бортовой аппара-

туры КА.

3. Разработана дискретная модель поверхности Земли.

4. Сформированы частные критерии оценки эффективности системы мо-

ниторинга.

5. Предложен обобщенный критерий эффективности системы монито-

ринга.

6. Обоснована необходимость разработки ИМ функционирования СГКМ

и выбор ее типа из класса непрерывно-дискретных моделей.

7. Разработана структура ИМ и ИП.

8. Имитационная модель процесса функционирования орбитальной

группировки космических аппаратов реализована в имитационной

программе на языке Delphi. К имитационной программе приложена

инструкция пользователя.

9. Проведены прогоны ИМ для различных состава (3, 5 и 9 спутников) и

параметров ОГ (высокие круговые, высокие эллиптические и смешан-

ные орбиты) с целью определения влияния параметров и структуры

ОГ на эффективность функционирования системы. На основании по-

лученных результатов сделаны следующие выводы:

эффективность функционирования системы повышается при ис-

пользовании в ОГ смешанных типов орбит;

с увеличением количества КА, входящих в ОГ, возрастает и эф-

фективность работы системы.

10. Результаты машинных экспериментов имитационной программы поз-

волили получить конкретные значения частных и обобщенного крите-

риев эффективности функционирования ОГ КА при выбранных зна-

чениях ее параметров. Так, из рассмотренных в работе вариантов ОГ в

качестве рациональной выбрана ОГ из девяти КА, выведенных на вы-

сокоэллиптические орбиты (высота перигея 23600 км, эксцентриситет

0,7, наклонение 65 град), средние полярные эллиптические (высота

перигея 15000 км, эксцентриситет 0,5, наклонение 90 град) и низ-

кие круговые (высота перигея 600 км, эксцентриситет 0, наклонение

орбиты 90 град). При времени моделирования 1 сутки обобщающий

критерий для этого варианта ОГ принимает значение 4,367.

241

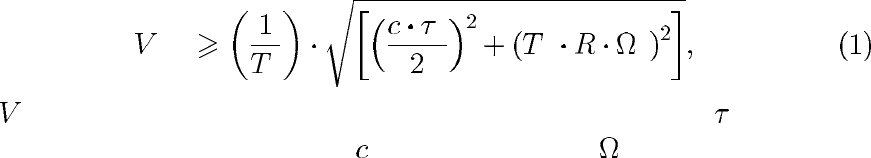
Приведенные результаты в виде имитационной модели, программы и ре-

зультатов машинных экспериментов могут быть использованы при про-

ектировании конкретной системы глобального космического мониторинга

земной поверхности.

А. А. Делекторский, В. Я. Плекин

Московский авиационный институт (государственный технический университет)

ИСПОЛЬЗОВАНИЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

ДЛЯ МЕЖДУОБЗОРНОЙ КОМПЕНСАЦИИ ПОМЕХ

Создание эффективных систем вторичной обработки информации по

данным РЛС кругового обзора предполагает разработку высоконадежных

алгоритмов обнаружения и сопровождения траекторий целей, находящихся

в зоне обзора. Как известно, решение задач траекторной обработки услож-

няется из-за действия пассивных помех, обусловленных нахождением в

зоне обзора РЛС неподвижных объектов, а также помех, обусловленных ве-

роятностью ложного обнаружения на этапе первичной обработки. Указан-

ные помехи ведут к появлению на входе устройства вторичной обработки

ложных отметок, что в свою очередь повышает вероятность обнаружения

ложных траекторий.

Таким образом, на первом этапе вторичной обработки должна быть

решена задача компенсации ложных отметок с тем, чтобы минимизировать

вероятность ложного автозахвата траектории.

Для компенсации ложных отметок можно использовать пространствен-

но-временные методы, позволяющие обеспечить селекцию движущихся

целей с малой радиальной составляющей скорости, а также тангенциаль-

ные цели. В частности, известен алгоритм междуобзорной компенсации

помех, основанный на использовании кадрового вычитающего устройства

(КВУ) [1]. Указанный метод обеспечивает селекцию целей, абсолютная

скорость движения которых удовлетворяет следующему условию:

min

п о

где

min

– минимальная абсолютная скорость движения цели;

– длитель-

ность зондирующего импульса;

– скорость света;

– угловая скорость

242

вращения антенны в режиме обзора;

– период повторения зондирующих

сигналов;

– дальность до цели;

– период обзора.

Для расширения функциональных возможностей и классов обнаружи-

ваемых целей, а также повышения надежности компенсации помех можно

использовать измеренные значения координат отметок движущихся це-

лей и помех, полученных в каждом цикле обзора РЛС. Алгоритм работы

устройства междуобзорной компенсации (УМК), основанный на исполь-

зовании координатной информации, описан в [2].

Указанные алгоритмы и устройства позволяют скомпенсировать только

один тип ложных отметок, а именно те отметки, появление которых на

входе устройства вторичной обработки обусловлено отражением от непо-

движных объектов. Отметки же, являющиеся результатом ложного обнару-

жения на этапе первичной обработки, очевидно, не будут скомпенсированы

ввиду того, что их появление во времени и пространстве носит случайный

характер.

Поэтому для общего решения задачи был разработан и предложен ал-

горитм, в основе которого лежит анализ детализирующих коэффициен-

тов дискретного вейвлет-преобразования сигнала, поступающего на вход

устройства вторичной обработки. Сигналом в данном случае является

пространственно-временная функция, характеризующая зависимость ко-

ординаты (дальности) цели, находящейся в зоне обзора, от времени на-

блюдения.

Предположим, что в зоне обзора находится цель, движущаяся с посто-

янной скоростью. Ввиду наличия вероятности ложного обнаружения на

этапе первичной обработки на вход устройства вторичной обработки по-

ступают как координаты движущейся цели, так и ложные отметки, число

которых является случайным. Координаты цели и ложные отметки во вре-

мени образуют дискретные функции

с интервалом дискретизации,

равным

Суть предлагаемого метода компенсации заключается в вейвлет-разло-

жении пространственно-временных функций

, представляющих собой

все возможные наборы отсчетов координат, поступающих на вход устрой-

ства вторичной обработки за время наблюдения и дальнейшего анализа де-

тализирующих коэффициентов вейвлет-преобразования на разных уровнях

разрешения. Возможность компенсации ложных отметок основана на том,

что, в случае использования вейвлета Хаара, детализирующие коэффици-

енты первого уровня разрешения вейвлет-преобразования функции, описы-

вающей изменение координаты движущейся с постоянной скоростью цели,

характеризуются свойством постоянства. То есть детализирующие коэф-

243

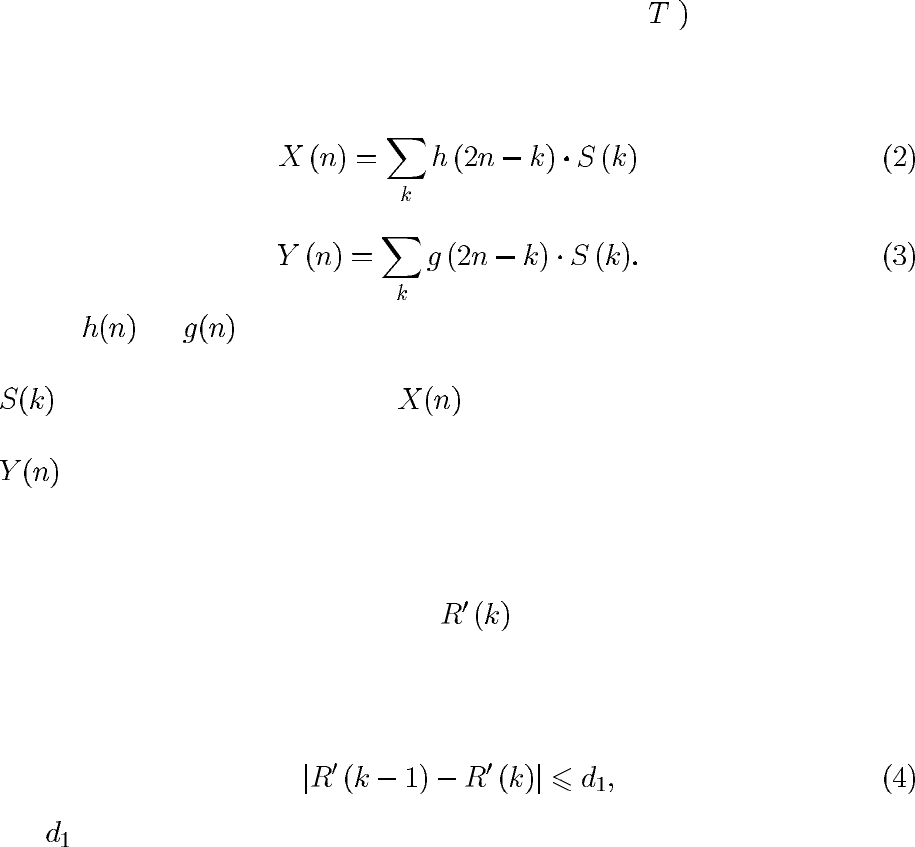
фициенты первого уровня разрешения есть величины, пропорциональные

приращению координаты цели за один цикл обзора. При этом отметки,

принадлежащие помехам, не обладают вышеуказанной закономерностью,

и детализирующие коэффициенты вейвлет-преобразования первого уровня

разрешения для них не являются постоянными величинами. Таким обра-

зом, появляется возможность селектировать отметки движущихся целей и

компенсировать ложные отметки.

Ввиду того, что анализируемая пространственно-временная функция яв-

ляется дискретной (интервал дискретизации равен

, предлагается ис-

пользовать дискретное вейвлет-преобразование, которое описывается со-

отношениями [3, 4]:

Здесь и – дискретные импульсные характеристики низкоча-

стотного (НЧ) и высокочастотного (ВЧ) вейвлет-фильтров соответственно;

– анализируемый сигнал; – аппроксимирующие коэффициен-

ты вейвлет-преобразования (НЧ составляющая анализируемого сигнала);

– детализирующие коэффициенты вейвлет-преобразования (ВЧ со-

ставляющая анализируемого сигнала).

Подчеркивая прямую связь детализирующих коэффициентов вейвлет-

преобразования первого уровня разрешения с приращением координаты

за один цикл обзора, обозначим их

Решение о том, что анализируемая функция является дискретной после-

довательностью значений координат равномерно движущейся цели, выно-

сится при выполнении следующего условия:

где – порог, зависящий от точности измерения координат.

Следует отметить, что минимальное значение порога ограничивается

точностью измерения координат. При выборе порога следует также учи-

тывать возможные случайные изменения скорости целей.

Характер расположения отметок до компенсации представлен на рис. 1,

а; после компенсации – на рис. 1, б.

В случае наличия в зоне обзора РЛС целей, движущихся с ускорени-

ем, их селекция и компенсация ложных отметок осуществляется при усло-

вии постоянства детализирующих коэффициентов вейвлет-преобразования

244

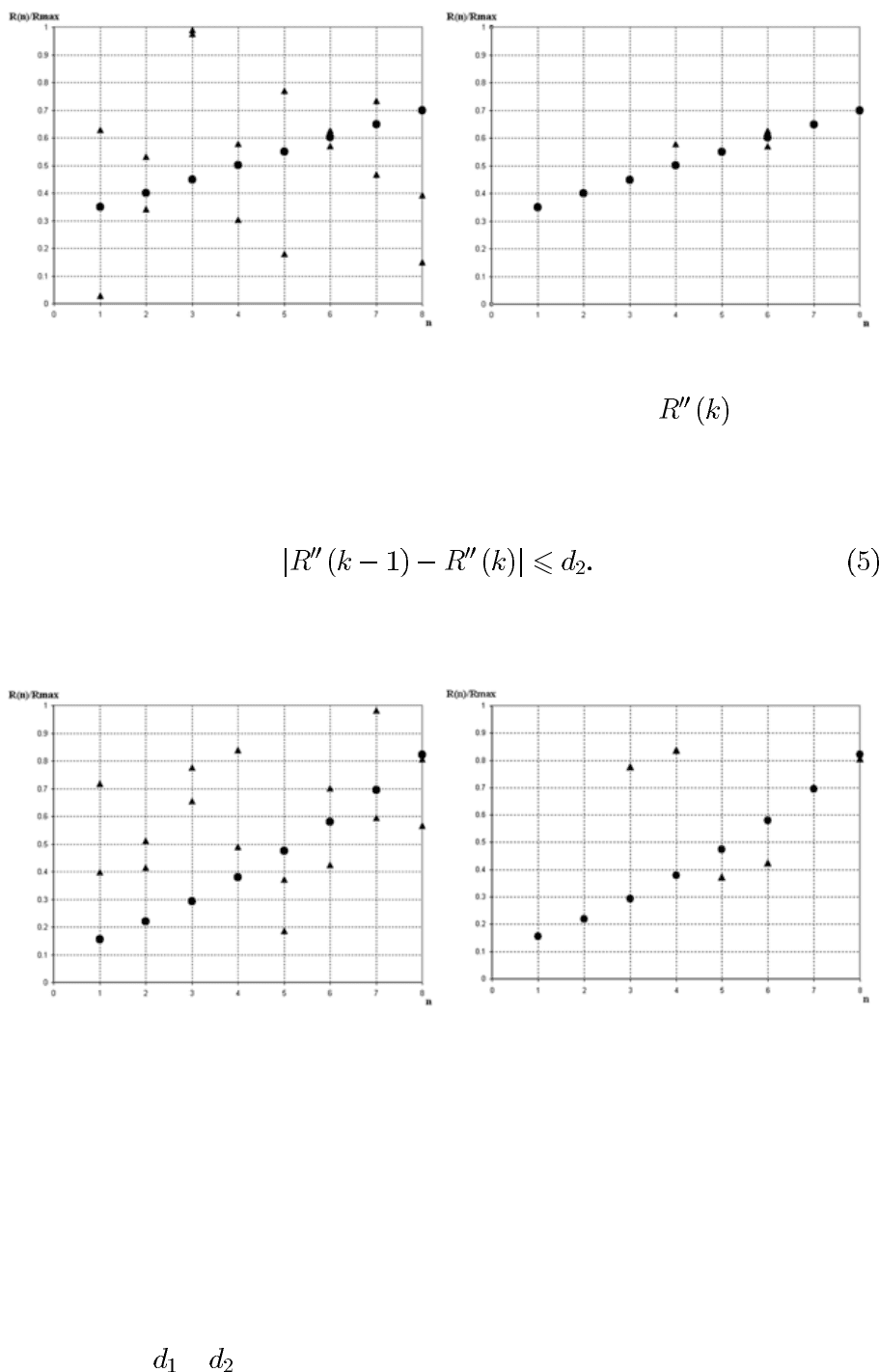
Рис. 1. Расположение отметок при селекции целей, движущихся с постоянной скоростью

второго уровня разрешения. Величина коэффициента пропорцио-

нальна изменению приращения координаты за период наблюдения.

Решение о том, что анализируемая функция является последовательно-

стью координат цели, выносится при выполнении следующего условия:

Характер расположения отметок до компенсации представлен на рис. 2,

а; после компенсации – на рис. 2, б.

Рис. 2. Расположение отметок при селекции цели, движущейся с ускорением

При практической реализации алгоритма нет необходимости в накоп-

лении данных о координатах отметок в течение длительного промежутка

времени, так как для вейвлет-преобразования на основе вейвлета Хаара

достаточно использовать два отсчета анализируемой функции. Таким об-

разом, существует возможность динамического расчета детализирующих

коэффициентов с использованием данных о координатах отметок, посту-

пающих на вход устройства вторичной обработки в каждом цикле обзора.

При снижении точности измерения координат значения порогов приня-

тия решения

и , фигурирующих в формулах (4) и (5) соответственно,

245

необходимо повысить, что, в свою очередь, ведет к снижению эффектив-

ности компенсации ложных отметок.

Для оценки эффективности предложенного алгоритма компенсации

ложных отметок было проведено статистическое моделирование на ЭВМ,

результаты которого представлены на рис. 3. На этом рисунке изображе-

на зависимость коэффициента компенсации

кпс

от точности измерения

координаты (дальности). Указанный коэффициент характеризует степень

компенсации ложных отметок.

Рис. 3. Зависимость коэффициента компенсации от точности измерения дальности

При моделировании учитывалась удельная плотность ложных отметок,

рассчитываемая по формуле

ло

где

ло

– общее число ложных отметок в зоне обзора; – максимальная

дальность измерения.

Результаты моделирования показали, что с увеличением удельной плот-

ности ложных отметок, находящихся в зоне обзора, качество компенсации

снижается, так как при этом возрастает вероятность того, что значения

разностей рассчитанных детализирующих коэффициентов попадут в до-

верительные интервалы, обусловленные значениями порогов принятия ре-

шения

и .

При моделировании значение величины

задано равным 150 км.

Блок-схема предложенного алгоритма компенсации ложных отметок с

использованием вейвлет-преобразования представлена на рис. 4.

246

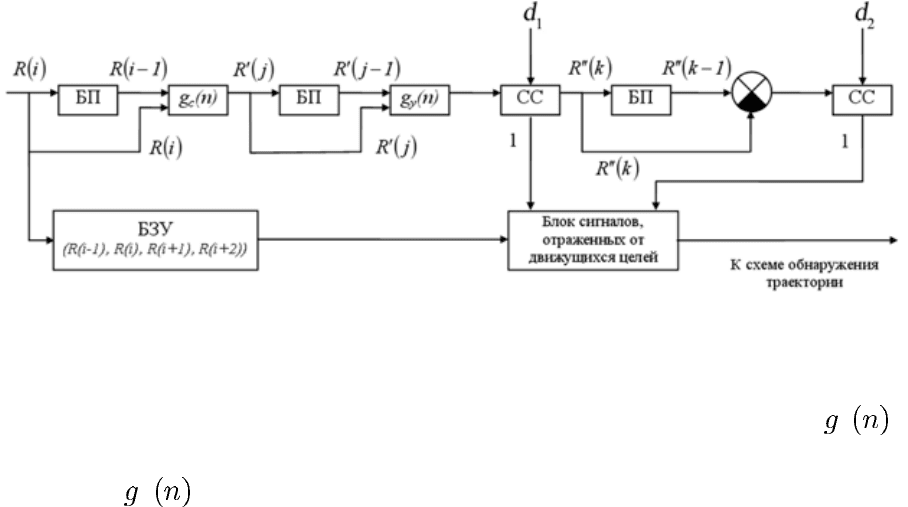
Рис. 4. Блок-схема алгоритма компенсации ложных отметок

На рис. 4 приняты следующие обозначения:

БП – блок памяти; БЗУ – буферное запоминающее устройство;

–

фильтр приращения координаты (ВЧ вейвлет-фильтр первого уровня раз-

решения);

– фильтр изменения приращения координаты (ВЧ вейвлет-

фильтр второго уровня разрешения); СС – схема сравнения.

При использовании вейвлет-преобразования для компенсации ложных

отметок решается задача поиска гладких (регулярных) пространственно-

временных функций, так как именно такого рода функции описывают дви-

жение реальных целей. Высокочастотный фильтр в данной схеме обладает

способностью наиболее эффективно выделить сингулярность (неоднород-

ность) анализируемой функции на определенном уровне разрешения.

Таким образом, предложен новый метод, который позволяет осуществ-

лять эффективную компенсацию ложных отметок и селекцию движущихся

целей, находящихся в зоне обзора.

Библиографический список

1. Плекин В.Я. Цифровые устройства селекции движущихся целей. М. – “САЙНС –

ПРЕСС”, 2003.

2. Плекин В.Я., Корольков Д.В. Устройство межобзорной компенсации помех для

когерентно-импульсной РЛС. Патент Российской Федерации №2031414. Приоритет

от 1.03.1991. Бюллетень №8. 20.03.1995.

3. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование // Успехи

физических наук. Т. 171. Май 2001. № 5.

4. Яковлев А.Н. Основы вейвлет-преобразования сигналов. – М.: “САЙНС-ПРЕСС”,

2003.

247

В. Я. Плекин, А. Б. Русскин

Московский авиационный институт (государственный технический университет)

ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ

ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

Развитие современных радиолокационных и радионавигационных си-

стем ставит задачу применения новых максимально надежных и произво-

дительных методов и средств цифровой обработки сигналов. Наличие шу-

мовой составляющей является неотъемлемой частью принимаемого сиг-

нала. При решении задачи распознавания изображений основным сред-

ством снижения влияния шумов является его предварительная фильтра-

ция, от качественных показателей которой зависит эффективность работы

всей системы. В связи с этим в качестве метода фильтрации изображений

предлагается использовать способ линейной фильтрации с использованием

вейвлет-преобразования (ВП).

Предлагаемый алгоритм основан на совместном выполнении опера-

ции дискретного вейвлет-преобразования изображения (ДВПИ) и про-

цедуры пороговой фильтрации (ППФ), что позволяет осуществлять

очистку изображения от различных видов шумов при минимальном ис-

кажении полезной составляющей сигнала, а также проводить фильтрацию

на основе масштабного признака.

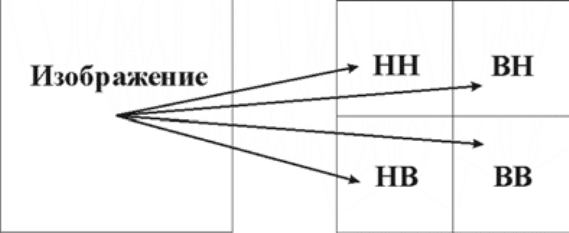
Рис. 1. Ортогональное вейвлет-разложение изображения

Рассмотрим особенности предлагаемого алгоритма. На основе частот-

ного подхода к ВП в результате выполнения ортогонального разложения

с ДВПИ входной сигнал делится (фильтруется) на четыре изображения:

НН, ВН, НВ, ВВ, характеризующие соответствующий вид фильтрации

по заданному геометрическому направлению (рис .1) [1]. Так, составля-

ющие ВН, НВ и ВВ соответствуют высокочастотной (ВЧ) фильтрации в

горизонтальном, вертикальном и диагональном направлениях и являют-

ся детализирующими коэффициентами разложения. Изображение НН есть

результат низкочастотной (НЧ) фильтрации по горизонтали и вертикали.

248

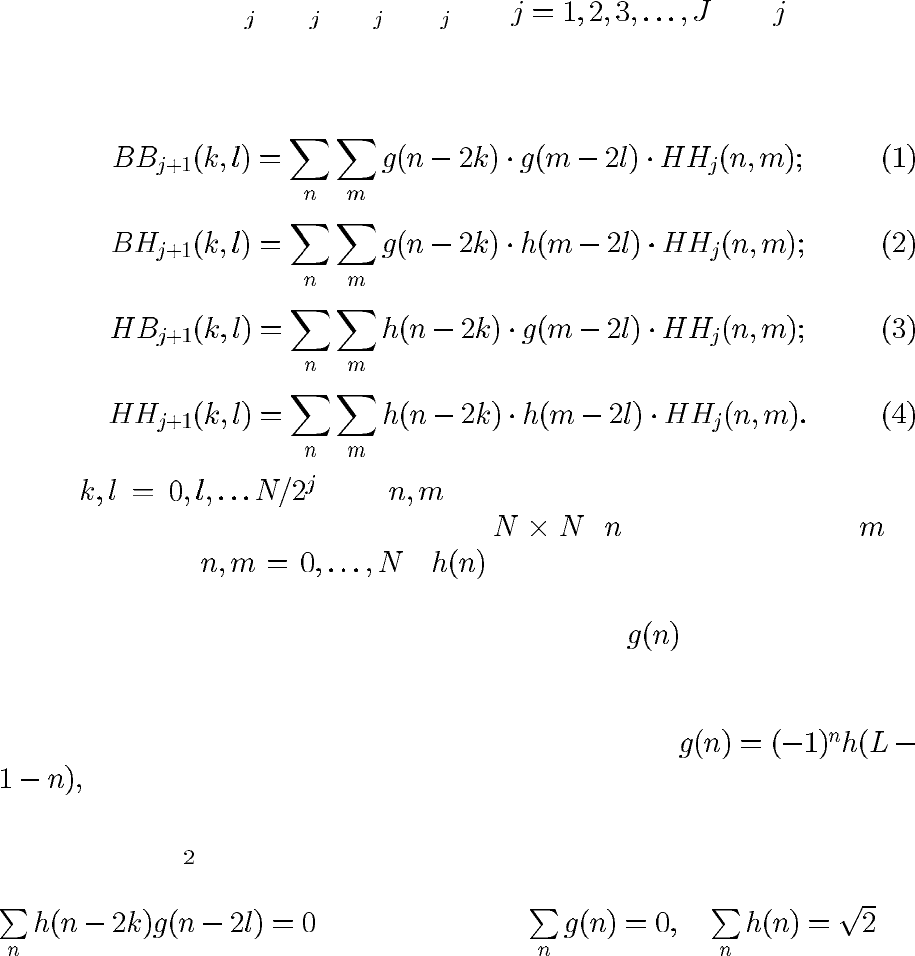
Оно содержит основную информацию об исходном сигнале и является

его аппроксимацией. На следующем шаге преобразования данное изобра-

жение используется в качестве исходного. Таким образом, многократное

применение вейвлет-разложения преобразует входной сигнал в набор изоб-

ражений, одно из которых является сглаженным (аппроксимирующим),

а другие — уточняющими (детализирующими) составляющими. Данный

способ двумерного кратномасштабного разложения изображения лежит в

основе алгоритма пирамидального кодирования [2, 3]. При этом основани-

ем вейвлет-пирамиды является исходное изображение, а вершиной - НЧ

составляющая самого верхнего уровня разложения. При пирамидальном

кодировании важное место занимает тип используемого в ДВПИ вейвле-

та, так как от него зависят свойства получаемых в результате разложения

уровней разрешения [3].

Изображения НВ

,ВН,ВВ,НН при (где указывает

номера уровней разложения) формируются с использованием рекуррент-

ных алгоритмов [2, 3]:

Здесь ; НН( ) - интенсивность элемента матрицы

исходного изображения размерностью

; — номер строки; —

номер столбца (

); - весовая функция квадратурного

вейвлет-фильтра, порождающая следующий уровень пирамиды, которой в

частотной области соответствует НЧ фильтрация; - весовая функция

квадратурного вейвлет-фильтра, которой в частотной области соответству-

ет ВЧ фильтрация.

При этом весовые функции связаны соотношением

где L – порядок фильтра.

Максимальное число уровней пирамиды при таком разложении со-

ставляет J=log

(N). В случае конечной длины импульсной характери-

стики (КИХ) фильтров на них накладываются условия ортогональности

и нормировки [4].

249

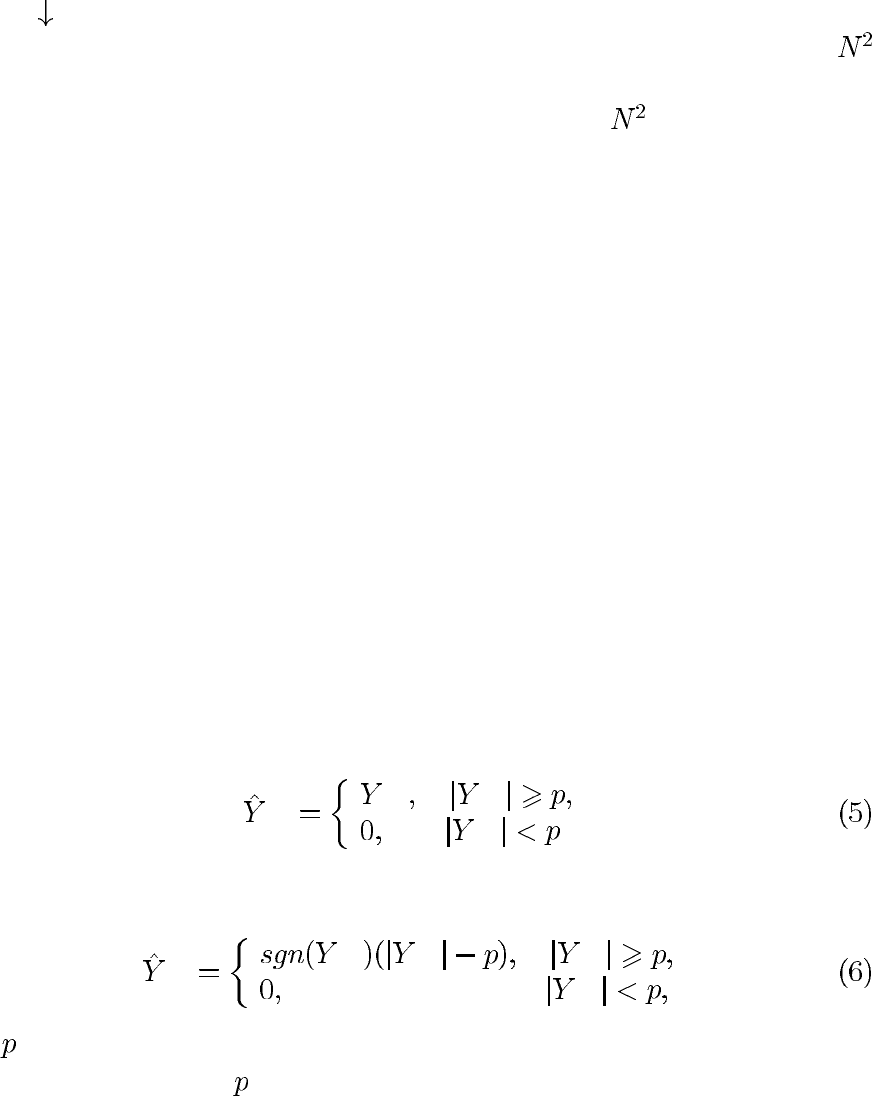
Каждый последующий уровень разложения j=1,2,3,. . . вычисляется по

формулам (1)-(4), при этом размерности полученных изображений умень-

шаются вдвое. Это обусловлено тем, что полоса пропускания квадратурных

вейвлет-фильтров равна половине ширины спектра сигнала и они переда-

ют только половину всех частотных компонентов. Не попавшие в полосу

прозрачности составляющие удаляются, для чего вводится операция деци-

мации

2, т.е. прореживание в два раза (множитель 2 при аргументахkиlв

формулах (1)-(4)). Таким образом, исходное изображение, содержащее

отсчетов, в результате пирамидального построения преобразуется в набор

изображений в общей сложности содержащих те же

элементов.

Разделение на НЧ (аппроксимирующую) и ВЧ (детализирующие) со-

ставляющие сигнала формирует возможность очистки изображения от шу-

ма путем ограничения уровня детализирующих коэффициентов [4]. Шум

в большей степени содержится в ВЧ составляющих и представляет со-

бой сигнал, меньший по модулю, чем полезный. Поэтому для его удаления

используется ППФ детализирующих коэффициентов, позволяющая выпол-

нить пространственно-частотную фильтрацию изображения, разложенного

по уровням разрешения. При пороговой фильтрации возможно использо-

вание разных типов порогов: жесткий или мягкий, и различные правила

выбора порога: адаптивный, эвристический, минимаксный. Это позволя-

ет устанавливать пороговый уровень для каждого коэффициента отдельно,

что дает возможность строить адаптивные к изменениям сигнала способы

очистки от шума.

Таким образом, фильтрация изображения осуществляется путем приме-

нения ППФ к полученным в результате разложения ВЧ трансформантам

на основе:

жесткой пороговой обработки:

ВЧ

ВЧ ВЧ

ВЧ

или мягкой пороговой обработки:

ВЧ

ВЧ ВЧ ВЧ

ВЧ

где – порог.

При выборе порога

следует иметь в виду, что его значение существен-

но влияет на качество фильтрации.

После выполнения пороговой процедуры осуществляется восстановле-

ние исходного изображения из НЧ и фильтрованных ВЧ составляющих,

250