Колистратова Л.Ф. Сборник задач по электромагнетизму
Подождите немного. Документ загружается.

(ε = 1 вне листа стекла), тогда
.
ε
ρd
E
0
Рис. 1.6
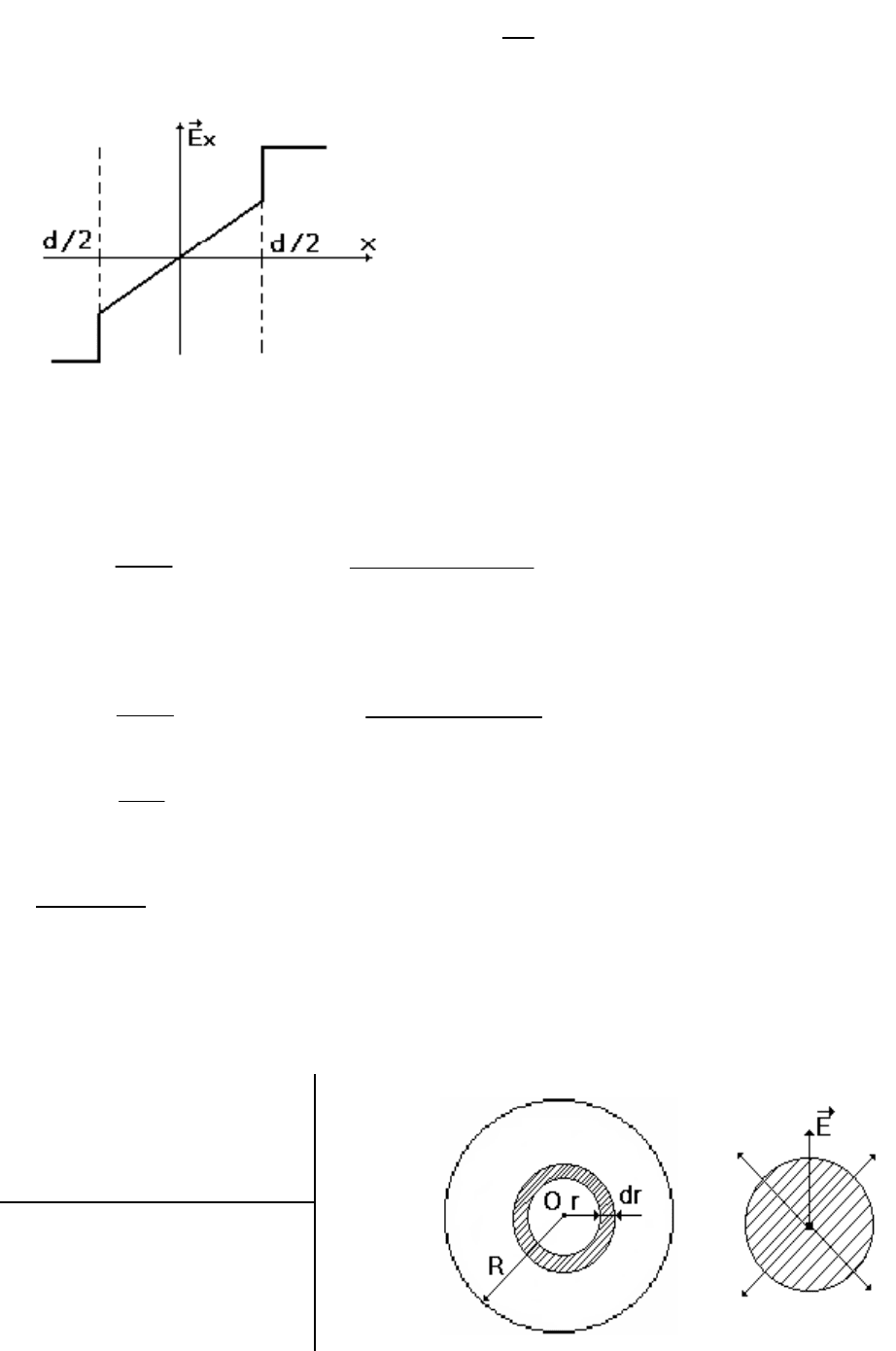
График зависимости проекции
вектора напряженности на ось Х от
координаты Х представлен на рис. 1.6
Отметим, что при переходе из стекла в
воздух модуль вектора скачком
увеличивается в ε раз.
Найдем теперь численные значения напряженности в точках А, B, С.
1. Е
А
= 0 (х = 0).
2.
;
4εε
dρ
E
0
B
.B/м80,7
108,8574
10210
E
12
26
B
3. Е
С
(два значения):
;
2εε
dρ
E
0
C1
.B/м161,4
108,8572
10210
E
12
26
C1
;
2ε
dρ
E
0
C2
1130EE
1c2c
В/м.
Задача 6. Эбонитовый простой шар (ε = 3) радиусом R = 5 см несет заряд,
равномерно распределенный с объемной плотностью ρ = 10 нКл/м
3
. Определить
напряженность электрического поля Е в толчках (рис 1.7): 1) на расстоянии r
1
= 3 см
от центра сферы; 2) на поверхности сферы; 3) на расстоянии r
2
=10 см от центра
сферы. Построить график зависимости Е(r).
Дано:
ε = 3;
R = 5 см = 5
.
10
-2
м
ρ = 10 нКл/м
3
= 10
-8
Кл/м
3
Е-?
Решение
Рис. 1.7
11
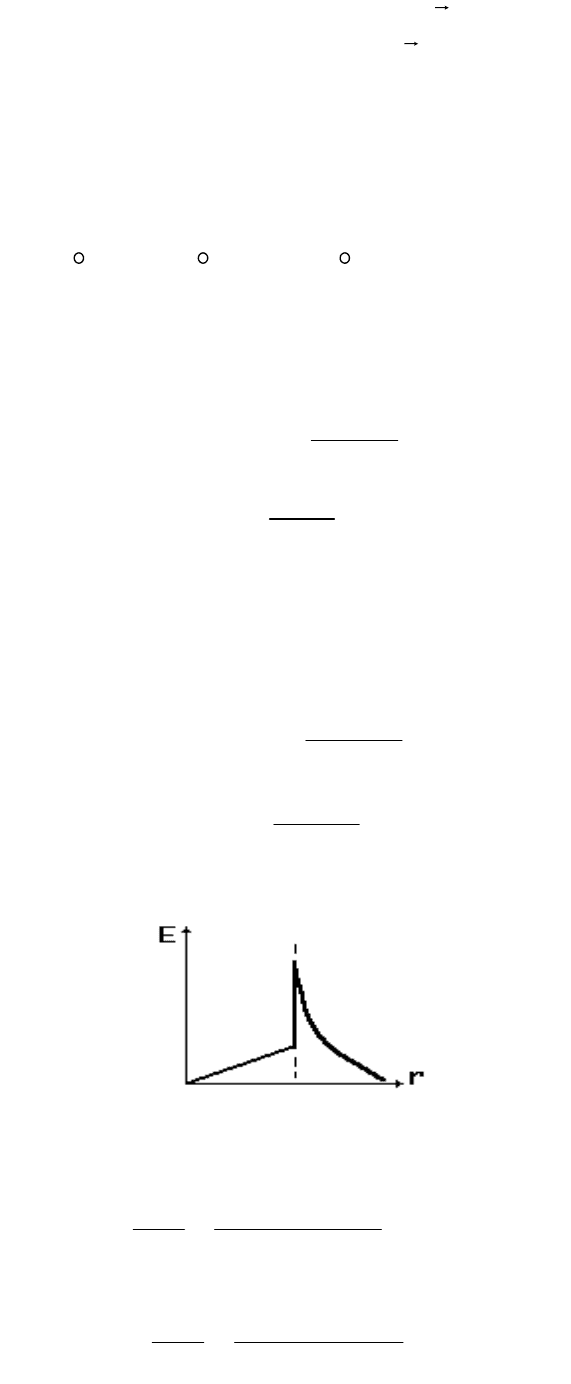
Применим метод Гаусса. Ввиду сферически симметричного распределения
заряда ρ можно утверждать, что линии вектора
Е
в любой точке направлены
вдоль радиусов из точки О, и модуль вектора
Е
имеет одинаковое значение на
равных расстояниях от центра шара О. Следовательно, в качестве гауссовых
поверхностей следует выбрать сферы радиусом r с центром в точке О.
Рассмотрим две области пространства:
Первая область: r ≤ R
Поток вектора напряженности через гауссову сферу
S
2
SS
E
.r4πEESSdE)dSE()SdE(N
(1)
Заряд, попавший внутрь гауссовой сферы q = ρV
/
, где V
/
- объём гауссовой сферы.
q = 4 πr
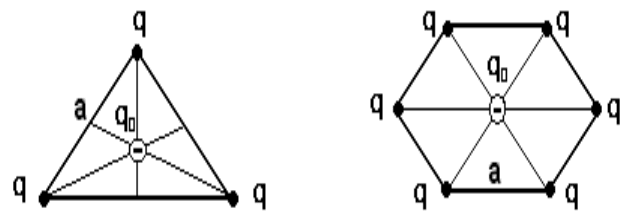
3
ρ /3. (2)
Объединим выражения (1) и (2) теоремой Гаусса:
ε3ε
r4πρ
r4πE
0
3
2
,
откуда
ε3ε
ρr
E
0
.
Вторая область: для точек, лежащих вне сферы, r > R. Поток вектора
напряженности через сферу радиусом r (как и в предыдущем случае)
N
Е
= E
.
4πr
2
.
Заряд, попавший внутрь сферы, - это весь заряд шара q = 4 πR
3
ρ/3.
ε3ε
R4πρ
r4πE
0
3
2
,
2
0
3
εr3ε
ρR
E
.
Построим график зависимости Е(r) (рис. 1.8).
Рис.1.8
Отметим, что на границе перехода из эбонита в воздух происходит скачок
напряженности. Она увеличивается в раз.
1.
.B/м3,37
108,8533
1031010
3εε
rρ
E
12
-2-9
0
1
)1r(
2. Е(R) (два значения):
.B/м6,28
108,8533
10510
3εε
Rρ
E
12
-2-8
0
)1R(
12

R
R
drE
0
)2R(
3εε
Rρ
E
= 3E(R)
1
= 18,8 В/м.
3.
.B/м103,6
1,0108,8533
)105(10
r3ε
Rρ
E
2
212
3-2-8
2
20
3
)2r(
Задача 7. Сплошной парафиновый шар (ε = 2) радиусом 10 см равномерно
заряжен с объемной плотностью 1 мкКл/м
3
. Определить потенциал φ электрического
поля в центре шара и на его поверхности. Построить график зависимости φ(r).
Дано:
ε = 2
R = 10 см =0,1 м
ρ = 1 мкКл/м
3
φ - ?
Решение
Воспользуемся соотношением между
напряженностью и потенциалом электростатического
поля:
E
= -grad φ. Поскольку поле шара обладает
сферической симметрией, то соотношение можно
записать в виде Е = -dφ/dr или - dφ = E
.
dr.
Интегрируя данное выражение, получаем:
Примем потенциал бесконечно
удаленной точки за нуль. Тогда
1
R
1
R
dr
E
, где φ
R
– потенциал на поверхности шара, или .
Выражение для напряженности поля в пространстве, окружающем шар, возьмем
из предыдущей задачи при условии, что r > R:
2
0
2
r3ε
ρR
E
Разность потенциалов между центром шара и его поверхностью
R
0
R
0
dr
E
, где φ
0
– потенциал в центре шара. Тогда
R
0
R0
drE
Напряженность поля возьмем из предыдущей задачи при условии r < R.
.
2
ε
1
1
3
ε
ρR
6
εε
ρR
3
ε
ρR
6
εε
ρR
φ
dr
3
εε
ρr
φ
φ
0
2
0
2
0
2
0
2
R
R
0
0
R
0
График зависимости φ(r) представлен на рис.1.9. Найдем численные значения φ
R
и φ
0:
.
B
472
2
2
1
1
10
8,85
3
0,1
10
φ
B,
377
10
8,85
3
0,1
10
φ
12
2
6
0
12
2
6
R
R
13
2
r
1
r
2
1
dr.
E
.
.
ю
.

R r
Рис. 1.9
1.3. Задачи для аудиторных занятий
1. Тонкий стержень длиной 10 см несет равномерно распределенный заряд 1 нКл.
Определить потенциал электрического поля в точке, лежащей на оси стержня на
расстоянии 20 см от ближайшего его конца.
Ответ: 36,5 В.
2. Три отрицательных заряда по 9 нКл каждый расположены в вершинах
равностороннего треугольника. Какой заряд нужно поместить в центре
треугольника, чтобы система находилась в равновесии?
Ответ: 5,2 нКл.
3. В трех вершинах квадрата со стороной 1 м расположены заряды величиной –2;
+4; -6 нКл. Найти напряженность в четвертой вершине.
Ответ: 43,56 В/м.
4. Круглая пластинка радиусом 8 см равномерно заряжена с поверхностной
плотностью 150 мкКл/м
2
. Определить напряженность поля в точке, лежащей на
расстоянии 6 см от пластинки на перпендикуляре к плоскости пластинки,
проходящем через её геометрический центр.
Ответ: 3,39
.
10
6
В/м.
5. Металлический шар имеет заряд 0,1 мкКл. На расстоянии, равном радиусу
шара от его поверхности, находится конец нити, вытянутой вдоль силовой линии.
Нить несёт равномерно распределенный по длине заряд 10 нКл. Длина нити
равна радиусу шара. Определить силу, действующую на нить, если радиус шара 10
см.
Ответ: 150 мкН.
6. Нарисовать графики зависимости напряженности поля и потенциала от
расстояния для следующего случая: бесконечный металлический цилиндр с
радиусом 10 см имеет заряд 60 нКл, окружен диэлектриком с диэлектрической
проницаемостью, равной 2, причем диэлектрик простирается до расстояния 20 см.
7. Две концентрические металлические сферы радиусами 4 см и 10 см имеют
соответственно заряды -2 нКл и 3 нКл. Пространство между сферами заполнено
эбонитом (ε = 3). Определить потенциал φ электрического поля на расстояниях 2 см,
6 см и 20 см от центра сфер.
Ответ: 540 В, 500 В, 225 В.
1.4. Задачи для самостоятельного решения
101. Два шарика одинакового радиуса и массы, подвешенные на нитях
одинаковой длины, опускаются в жидкий диэлектрик, плотность которого ρ
1
и
диэлектрическая проницаемость . Какова должна быть плотность ρ материала
шариков, чтобы углы расхождения нитей в воздухе и диэлектрике были
14
одинаковыми?
102. Шарик, имеющий массу 0,4 г и заряд 4,9 нКл, подвешен на нити в поле
плоского конденсатора, заряд которого 4,45 нКл и площадь пластин 50 см.
2
На
какой угол от вертикали отклонится при этом нить с шариком?
103. В центр квадрата, в вершинах которого находятся заряды по 20 нКл,
помещен отрицательный заряд. Найти величину этого заряда, если результирующая
сила, действующая на каждый заряд, равна нулю.
104. Отрицательный q
1
= -5q и положительный q
2
= +2q заряды закреплены на
расстоянии r друг от друга. Где на линии, соединяющей заряды, следует поместить
положительный заряд q
3
, чтобы он находился в равновесии?
105. В вершинах квадрата со стороной 10 см находятся одинаковые по величине
заряды q, но чередующиеся по знаку. Какая сила будет действовать на заряд +q,
помещенный в центр квадрата. q = 1нКл, Q = 10 нКл.
106. Два равных по величине заряда |q
1
| = |q
2
| = 3 нКл расположены в вершинах
острых углов равнобедренного прямоугольного треугольника на расстоянии 2 см.
Определить, с какой силой оба заряда действуют на третий заряд q
3
= +1 нКл,
находящийся в вершине прямого угла треугольника. Рассмотрите случаи, когда
первые два заряда: а) одноименные; б) разноименные.
107. Два одинаковых положительных заряда величиной 10 нКл каждый
расположены в вершинах равностороннего треугольника со стороной 10 см. Какая
сила будет действовать на заряд Q, помещенный в третьей вершине треугольника?
108. Два шарика массой 1 г каждый подвешены на нитях, верхние концы которых
соединены вместе. Длина каждой нити равна 10 см. Какие одинаковые заряды
необходимо сообщить шарикам, чтобы нити разошлись на угол 60
0
?
109. На бесконечной вертикально расположенной плоскости равномерно
распределен заряд с поверхностной плотностью 400 мкКл/м
2
. К плоскости на нити
подвешен шарик массой 10 г. Определить заряд шарика, если нить образует с
плоскостью угол 30
0
.
110. В вершинах правильного треугольника находятся одинаковые заряды q.
Какой величины заряд противоположного знака нужно ввести в центр
треугольника, чтобы система зарядов находилась в равновесии (рис.1.10)?
Рис. 1.10 Рис. 1.11
111. В вершинах правильного шестиугольника находятся одинаковые заряды q.
Какой величины заряд противоположного знака нужно ввести в центр
шестиугольника, чтобы система зарядов находилась в равновесии (рис.1.11)?
112. Два точечных заряда 6,7 и 13,2 нКл находятся на расстоянии 5 см друг от
15

друга. Найти напряженность электрического поля в точке, расположенной на
расстоянии 3 см от первого заряда и 4 см от второго.
113. В трех вершинах квадрата со стороной 40 см находятся одинаковые
положительные заряды по 5 нКл каждый. Найти напряженность поля в четвертой
вершине.
114. В вершинах квадрата расположены заряды 10,33; -0,66; 0,99;-1,32 нКл.
Определить потенциал поля в центре квадрата, если его диагональ равна 20 см.
115. Сто одинаковых капель ртути, заряженных до потенциала φ = 20 В,
сливаются в одну большую каплю. Каков потенциал образовавшейся капли?
116. В вершинах ромба с диагоналями 20 и 40 см находятся последовательно
заряды q, 4q, 20q и 8q. Чему равна напряженность в центре ромба и какой угол она
составляет с меньшей диагональю (q = 10 нКл)?
117. В двух вершинах равностороннего треугольника со стороной 5 см находятся
заряды по 5 мкКл. Найти напряженность поля в третьей вершине треугольника.
118. Три одинаковых заряда величиной по 1 нКл каждый расположены в
вершинах прямоугольного треугольника, имеющего катеты а = 40 см и b = 30 см.
Найти напряженность электростатического поля, создаваемого всеми зарядами в
точке пересечения гипотенузы с перпендикуляром, опущенным на нее из вершины
прямого угла.
119. В пяти вершинах шестиугольника со стороной 5 см находятся одинаковые
заряды величиной 5 нКл. Найти напряженность и потенциал в шестой вершине
треугольника.
120. Два одинаковых положительных заряда q = 0,1мкКл находятся в воздухе на
расстоянии 8 см друг от друга. Определить напряженность электростатического
поля в точке, расположенной на расстоянии r = 5 см от каждого заряда.
121. Расстояние между двумя точечными зарядами q
1
= 7
.
10
-9
Кл и
q
2
= -14
.
10
-9
Кл
равно 100 см. Найти напряженность электростатического поля в точке, находящейся
на расстоянии 60 см от положительного заряда и 80 см от отрицательного.
122. В вершинах равностороннего треугольника со стороной 0,2 м помещены
заряды по 2 нКл. Найти напряженность электростатического поля в точке В,
расположенной на середине стороны треугольника (рис.1.12).
Рис.1.12 Рис.1.13
123. Заряды 10 мкКл и -10 мкКл находятся на расстоянии 10 см. Определить
напряженность электростатического поля в точке А, лежащей на перпендикуляре к
линии, соединяющей заряды, и удаленной от q
1
на расстояние r = 10 см (рис.1.13).
124. Три одинаковых заряда величиной 1 нКл каждый расположены в вершинах
16
прямоугольного треугольника, имеющего катеты а = 40 см и b = 30 см. Найти
напряженность электростатического поля, создаваемого всеми зарядами в точке
пересечения гипотенузы с перпендикуляром, опущенным на нее из вершины
прямого угла.
125. По тонкой нити, изогнутой по дуге окружности радиусом 10 см, равномерно
распределен заряд 20 нКл. Определить потенциал электростатического поля φ,
создаваемого этим зарядом в центре кривизны дуги, если длина нити равна четверти
длины окружности (рис.1.14).
Рис.1.14 Рис.1.15 Рис.1.16
126. По тонкому кольцу радиусом 8 см равномерно распределен заряд с
линейной плотностью 10 нКл/м. Определить напряженность электростатического
поля
Е
в точке О, равноудаленной от всех точек кольца на расстояние 10 см
(рис.1.15).
127. Тонкое полукольцо радиусом 10 см равномерно заряжено с линейной
плотностью заряда 5 нКл/м. Определить напряженность электростатического поля
Е
в центре кривизны полукольца (рис.1.16).
128. Заряд 10 нКл равномерно распределен по дуге окружности, радиус которой
1 см, а угол раствора 2π/3. Определить напряженность электростатического поля
Е
в центре кривизны дуги.
129. Параллельно бесконечной плоскости, заряженной с поверхностной
плотностью заряда 4 мкКл/м
2
, расположена прямая бесконечная нить, заряженная с
линейной плотностью заряда 100 нКл/м
2
. Определить силу, действующую со
стороны плоскости на отрезок нити длиной 1 м.
130. С какой силой, приходящейся на единицу площади, отталкиваются две
одноименно заряженные бесконечно протяженные плоскости с одинаковой
поверхностной плотностью заряда -2 мкКл/м
2
?
131. По дуге, длина которой равна 2/3 длины окружности радиусом 10 см,
равномерно распределен заряд с линейной плотностью 0,2 мкКл/м. Определить
потенциал электростатического поля в центре кривизны дуги.
132. Полуокружность радиусом 2 м равномерно заряжена (q = 10
-9
Кл).
Определить напряженность электрического поля, созданного этим зарядом в
геометрическом центре полуокружности.
133. Тонкое кольцо радиусом 8 см несет заряд, равномерно распределенный с
линейной плотностью 10 нКл/см. Какова напряженность электрического поля в
точке, равноудаленной от всех точек кольца на расстояние 10 см?
17
134. Тонкий стержень длиной 12 см заряжен с линейной плотностью 200 нКл/см.
Найти напряженность электрического поля в точке, находящейся на расстоянии 5 см
от стержня, против его середины.
135. Тонкий стержень длиной 10 см заряжен с линейной плотностью заряда
400 нКл/м. Найти напряженность электростатического поля в точке А, которая
удалена от конца стержня на расстояние 8 см перпендикулярно стержню (рис. 1.17).
Рис.1.17 Рис.1.18
136. Найти напряженность электростатического поля, которое создают в точке А
параллельные равномерно заряженные с линейной плотностью заряда 10
-8
Кл/м
тонкие нити длиной 0,5 м. Точка А находится в одной плоскости с нитями и удалена
от каждой нити на расстояние 0,2 м (рис.1.18).
137. Прямая бесконечная нить, равномерно заряженная с линейной плотностью
заряда 0,3 мкКл/м
2
, и отрезок нити длиной 20 см, равномерно заряженный с
линейной плотностью заряда 0,2 мкКл/м
2
, расположены в одной плоскости
перпендикулярно друг другу на расстоянии 10 см. Определить силу взаимодействия
между ними (рис. 1.19).
Рис.1.19
138. Электрическое поле создано бесконечной прямой, равномерно заряженной
нитью с линейной плотностью заряда 0,3 мкКл/м. Определить поток N
E
вектора
напряженности через прямоугольную площадку, две большие стороны которой
параллельны заряженной нити и одинаково удалены от нее на расстояние 20 см.
Стороны площадки имеют размеры a = 20 см, b = 40 см.
139. Имеются две металлические концентрические сферы, радиусы которых 5 и
10 см и заряды 2
.
10
-8
и –10
-8
Кл. Определить напряженность поля, созданного этими
сферами, в точках, отстоящих от центров сфер на расстояния 3, 8 и 14 см. Построить
график зависимости напряженности поля от расстояния точки от центра сфер.
140. Металлически заряженный шар радиусом 5 см окружен сферическим слоем
диэлектрика толщиной 5 см. Диэлектрическая проницаемость слоя равна 3. Заряд
шара 3,6 нКл. Найти напряженность поля в точках, лежащих на расстояниях 6 см и
18
12 см от центра шара.
141. Два бесконечных тонкостенных коаксиaльных цилиндра радиусами 5 см и
10 см равномерно заряжены с поверхностными плотностями 10 нКл/м
2
и
-3 нКл/м
2
. Пространство между цилиндрами заполнено парафином ( = 2).
Определить напряженность поля в точках, находящихся на расстояниях 2 см, 6 см,
15 см от оси цилиндров.
142. Бесконечно длинная тонкая прямая нить несет равномерно распределенный
по длине нити заряд с линейной плотностью 0,01 мкКл/м. Определить разность
потенциалов двух точек поля, удаленных от нити на 2 см и 4 см.
143. Большая плоская пластина толщиной 1 см несет заряд, равномерно
распределенный по поверхности с объемной плотностью 100 нКл/м
3
. Найти
напряженность электрического поля вблизи центральной части пластины на малом
расстоянии от её поверхности.
144. Длинный парафиновый цилиндр радиусом 2 см несёт заряд, равномерно
распределенный по объёму с объемной плотностью 10 нКл/м
3
. Определить
напряженность поля в точках, находящихся от оси цилиндра на расстояниях 1 см и
3 см. Обе точки равноудалены от концов цилиндра. Построить график зависимости
Е(r).
145. Сплошной шар из диэлектрика ( = 3) радиусом 10 см заряжен с объёмной
плотностью 50 нКл/м
3
. Напряженность электрического поля внутри и на
поверхности такого шара выражается формулой Е = ρ
.
r/3
.
0
, где r – расстояние от
центра шара до точки, в которой вычисляется напряженность поля. Вычислить
разность потенциалов между центром шара и точками, лежащими на его
поверхности.
146. Эбонитовый толстостенный шар ( = 3) несет равномерно распределенный
по объёму заряд 2 мкКл/м
3
. Внутренний радиус шара 3 см, наружный 6 см.
Определить потенциал шара в следующих точках: 1) на наружной поверхности
шара, 2) на внутренней поверхности шара, 3) в центре шара.
147. Две металлические концентрические сферы имеют радиусы R
1
и R
2
. На
внутренней сфере находится заряд q
1
, на внешней – заряд q
2
. Найти напряженность
Е и потенциал φ поля вне сфер, а также внутри малой и большой сфер.
148. Пластины плоского конденсатора площадью 0,01 м
2
каждая притягиваются с
силой 12 мН. Пространство между пластинами заполнено диэлектриком с = 2.
Определить: а) модуль вектора электрического смещения |D|; б) заряд каждой
пластины.
149. Тонкий стержень длиной 20 см равномерно заряжен с линейной плотностью
1 нКл/см. Определить напряженность поля, созданного стержнем в точке А на
продолжении его оси на расстоянии 10 см от ближнего конца, и силу
взаимодействия стержня и заряда 10
-8
Кл, если его поместить в точку А.
150. Прямая бесконечная нить, равномерно заряженная с линейной плотностью
3
.
10
-7
Кл/м, и отрезок другой нити длиной 20 см, равномерно заряженный с
линейной плотностью 2
.
10
-7
Кл/м, расположены в одной плоскости перпендикулярно
друг к другу на расстоянии 10 см. Определить силу взаимодействия между ними.
19

151. Прямая бесконечно тонкая нить несет равномерно распределённый по длине
заряд 1 мкКл/м. В плоскости, содержащей нить, перпендикулярно к нити находится
тонкий стержень длиной 10 см. Ближайший к нити конец стержня находится на
расстоянии 5 см от неё. Определить силу, действующую на стержень, если он
заряжен с линейной плотностью 0,1 мкКл/м.
152. Электрическое поле создано бесконечной плоскостью, заряженной с
поверхностной плотностью заряда 400 нКл/м
2
,и бесконечной прямой нитью,
заряженной с линейной плотностью заряда 100нКл/м. На расстоянии 10см от нити
находится точечный заряд 10 нКл. Определить величину и направление силы,
действующей на заряд, если заряд и нить лежат в одной плоскости, параллельной
заряженной плоскости (рис.1.20).
Рис.1.20
153. Между пластинами плоского воздушного конденсатора находится точечный
заряд 30 нКл. Поле конденсатора действует на заряд с силой 10 мН. Определить
силу взаимного притяжения пластин, если площадь каждой пластины 100 см.
2
154. Точечный заряд 25 нКл находится в поле, созданном прямым бесконечным
цилиндром радиусом 1 см, равномерно заряженным с поверхностной плотностью
заряда 0,2 нКл/см
2
. Определить силу, действующую на заряд, если заряд находится
на расстоянии 10 см от оси цилиндра.
155. На тонком полукольце радиусом 20 см равномерно распределен заряд
2
.
10
–6
Кл. Определить силу, действующую на точечный заряд 4
.
10
–8
Кл,
расположенный в центре кривизны полукольца.
2. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
2.1. Основные формулы
1. Работа электрических сил по переносу заряда q из точки с потенциалом φ
1
в
точку с потенциалом φ
2
А = q(φ
1
– φ
2
).
2. Работа по переносу точечного заряда q
1
в поле точечного заряда q
2
из точки 1
в точку 2
21
21
r
1
r
1
qkqA
,
где r
1
и r
2
– расстояния от точек 1 и 2 соответственно до заряда q
1
.
3. Работа по переносу заряда q
по любой траектории в неоднородном поле
20
