Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


ψ
1
= ki − z
1
− ωz
3
− ϕ
1
; ψ
2
=(ω − ω
∗
)β − ϕ
2
; ψ
3
= z
1
+ λz
2
.
T
i
ψ
i
(t)+ψ
i
=0,i=1, 2, 3
u
2
(ω, i ,z
1
,z
2
,z
3
)
ψ
i
=0
ψ
3
=0
¨z
2ψ
3
(t)+λ ˙z
2ψ
3
(t)+w
2
0
z
2ψ
3
=0
ξ =
λ
2w
0
ξ =1
λ =2w
0
.
u
2
=
J
0
L (ω − ω
∗
)(1 + 2w
0
(T
2
+ T
3
)) + L (ωz
3
+ z
1
)(T
2
+ T
3
)
T
2
T
3
k
+
ψ
1
T
1
k
+
+
2L
(ωz
3
+ z
1
)(J
0
w
0
+2z
1
)+L i k(z
1
+ z
3
)
J
0
k
− 2Lw
0
i + kω + r i +
+
w
0
L ω(2(z
1
+ z
3
) − w
0
z
2
)
k
−
2J
0
w
3
0
L T
2
T
3
((z
1
+ z
3
)+z
2
(T
2
T
3
)
T
2
T
3
βk
,
ψ
1
=
(T
2
+ T
3
)(2w
0
(z
1
+ z
3
)+β(ω − ω
∗
)) + z
1
+2w
0
z
2
− 2w
3
0
z
2
T
2
T
3
T
2
T
3
J
0
+
2w
0
(ω − ω
∗
)
J
0
J
0
=2,M
c
=5,J
0
=2,a=0.2,b=0.1,w
0
=10,L =0.1,k=1,r =10
ω
∗
=3,β=0.5,T
1
=0.4,T
2
=0.2,T
3
=0.5.

J(t)
J(t)
M
c
˙ν
1
(t)=ν
2
, ˙ν
2
(t)=−w
2
0
ν
1
,
˙
J(t)=ν
2
, ˙ν
3
(t)=0,M
c
= ν
3
.
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
˙ω(t)=
ki
− ν
3
− ν
2
ω
J
0
;
˙
i
(t)=
u
− kω − r i
L
;
˙ν
1
(t)=ν
2
;
˙ν
2
(t)=−w
2
0
ν
1
;
˙ν
3
(t)=0.
˙
J(t)
M
c
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
˙ω(t)=
ki
− ν
3
− ν
2
ω
J
0
;
˙ν
1
(t)=ν
2
;
˙ν
2
(t)=−w
2
0
ν
1
;
˙ν
3
(t)=0.

ν
1
,ν
2
ν
3
Ψ=
⎡
⎢
⎢
⎣
ν
1
− ˆν
1
ν
2
− ˆν
2
ν
3
− ˆν
3
⎤
⎥
⎥
⎦
,
˙
Ψ(t) − LΨ=0
L
ν
2
−
˙
ˆν
1
(t) − l
11
(ν
1
− ˆν
1
) − l
12
(ν
2
− ˆν
2
) − l
13
(ν
3
− ˆν
3
)=0;
− w
2
0
ν
1
−
˙
ˆν
2
(t) − l
21
(ν
1
− ˆν
1
) − l
22
(ν
2
− ˆν
2
) − l
23
(ν
3
− ˆν
3
)=0;
−
˙
ˆν
3
(t) − l
31
(ν
1
− ˆν
1
) − l
32
(ν
2
− ˆν
2
) − l
33
(ν
3
− ˆν
3
)=0.
l
ij
L ν
3
= ki − ν
2
ω − ˙ω(t)J
0
ν
2
−
˙
ˆν
1
(t) − l
11
(ν
1
− ˆν
1
) − l
12
(ν
2
− ˆν
2
) − l
13
(ki − ν
2
ω − ˙ω(t)J
0
− ˆν
3
)=0;
− w
2
0
ν
1
−
˙
ˆν
2
(t) − l
21
(ν
1
− ˆν
1
) − l
22
(ν
2
− ˆν
2
) − l
23
(ki − ν
2
ω − ˙ω(t)J
0
− ˆν
3
)=0;
−
˙
ˆν
3
(t) − l
31
(ν
1
− ˆν
1
) − l
32
(ν
2
− ˆν
2
) − l
33
(ki − ν
2
ω − ˙ω(t)J
0
− ˆν
3
)=0.
L
l
11
=0,l
12
=1+l
13
ω, l
21
= −w
2
0
,l
22
= l
23
ω, l
31
=0,l
32
= l
33
ω.
l
13
,l
23
l
33
L
L
det(pE − L)=
⎡
⎢
⎢
⎣
p −1 − l
13
ω −l
13
w
2
0
p − l
23
ω −l
23
0 −l
33
ωp− l
33
⎤
⎥
⎥
⎦
= p
3
− (l
33
+ l
23
ω)p
2
+(w
2
0
l
13
ω + w
2
0
)p + w
0
l
33
.
ω
Λ=(p
2
+ w
2
0
ω
2
λ
1
p + w
2
0
)(p + ω
2
λ
2
)=p
3
− (w
2
0
ω
2
λ
1
+ ω
2
λ
2
)p
2
+(w
2
0
+ w
2
0
ω
4
λ
1
λ
2
)p − w
2
0
ω
2
λ
2
,
λ
1
,λ
2
p
1,2
= −
1
2
ω
2
λ
1
w
2
0
±
w
0
2
ω
4
w
2
0
λ
2
1
− 4,p
3
= −ω
2
λ
2
,
λ
1
λ
2
L
l
13
,l
23
l
33

l
13
= ω
3
λ
1
λ
2
,l
23
= −ωw
2
0
λ
1
,l
33
= −ω
2
λ
2
.
L
−
˙
ˆν
1
(t)+(1− ω
4
λ
1
λ
2
)ˆν
2
− ω
3
λ
1
λ
2
(ki − ˙ω(t)J
0
− ˆν
3
)=0;
−
˙
ˆν
2
(t) − w
2
0
ˆν
1
− w
2
0
ω
2
λ
1
ˆν
2
+ ωw
2
0
λ
1
(ki − ˙ω(t)J
0
− ˆν
3
)=0;
−
˙
ˆν
3
(t) − ω
3
λ
2
ˆν
2
+ ω
2
λ
2
(ki − ˙ω(t)J
0
− ˆν
3
)=0.
z
1
=
ˆν
1
−
J
0
λ
1
λ
2
ω
4
4
z
2
=ˆν
2
+
J
0
w
2
0
λ
1
ω
2
2
z
3
=ˆν
3
+
J
0
λ
2
ω
3
3
ν
1
,ν
2
ν
3
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
˙z
1
(t)=(1−ω
4
λ
1
λ
2
)
z
2
−
J
0
w
2
0
λ
1
ω
2
2
− ω
3
λ
1
λ
2
ki
− z
3
+
J
0
λ
2
ω
3
3
=0;
˙z
2
(t)=−w
2
0
z
1
+
J
0
λ
1
λ
2
ω
4
4
− w
2
0
ω
2
λ
1
z
2
−
J
0
w
2
0
λ
1
ω
2
2
+
+ ωw
2
0
λ
1
ki
− z
3
+
J
0
λ
2
ω
3
3
=0;
˙z
3
(t)=−ω
3
λ
2
z
2
−
J
0
w
2
0
λ
1
ω
2
2
+ ω
2
λ
2
ki
− z
3
+
J
0
λ
2
ω
3
3
=0;
ˆν
1
= z
1
+
J
0
λ
1
λ
2
ω
4
4
;
ˆν
2
= z
2
−
J
0
w
2
0
λ
1
ω
2
2
;
ˆν
3
= z
3
−
J
0
λ
2
ω
3
3
;
u (x)=−
L
ν
2
(i −ν
3
− ν
2
ω)
kJ
0
+
L
(ν
3
− ki + ν
2
ω)
T
2
k
+
+
ˆ
˙ν
2
(t)ωL T
1
T
2
− i L kT
2
+ ν
3
L T
2
+ L ν
2
ωT
2
− J
0
L (ω − ω
∗
)
kT
1
T
2
,
ˆ
˙ν
2
(t)= ˙z
2
(t) − J
0
w
2
0
λ
1
ω ˙ω(t)=−w
2
0
λ
1
ω
ki − M
c
−
z
2
−
J
0
w
2
0
λ
1
ω
2
2
ω
−
−
w
2
0
z
1
+
J
0
λ
1
λ
2
ω
4
4
+ w
2
0
ω
2
λ
1
z
2
−
J
0
w
2
0
λ
1
ω
2
2
− ωw
2
0
λ
1
ki
− z
3
+
J
0
λ
2
ω
3
3
.
⎧
⎪
⎪
⎨
⎪
⎪
⎩
˙ω(t)=
ki
− M
c
− ωaw
0
cos w
0
t
J
0
+ a sin w
0
t
;
˙
i
(t)=
u
− kω − r i
L
,
λ
1
=1 λ
2
=0, 5 λ
3
=1, 5 T =0, 1
J
0
=1 a =0, 1 M
c
=0, 8 ω
∗
=3 w
0
=3
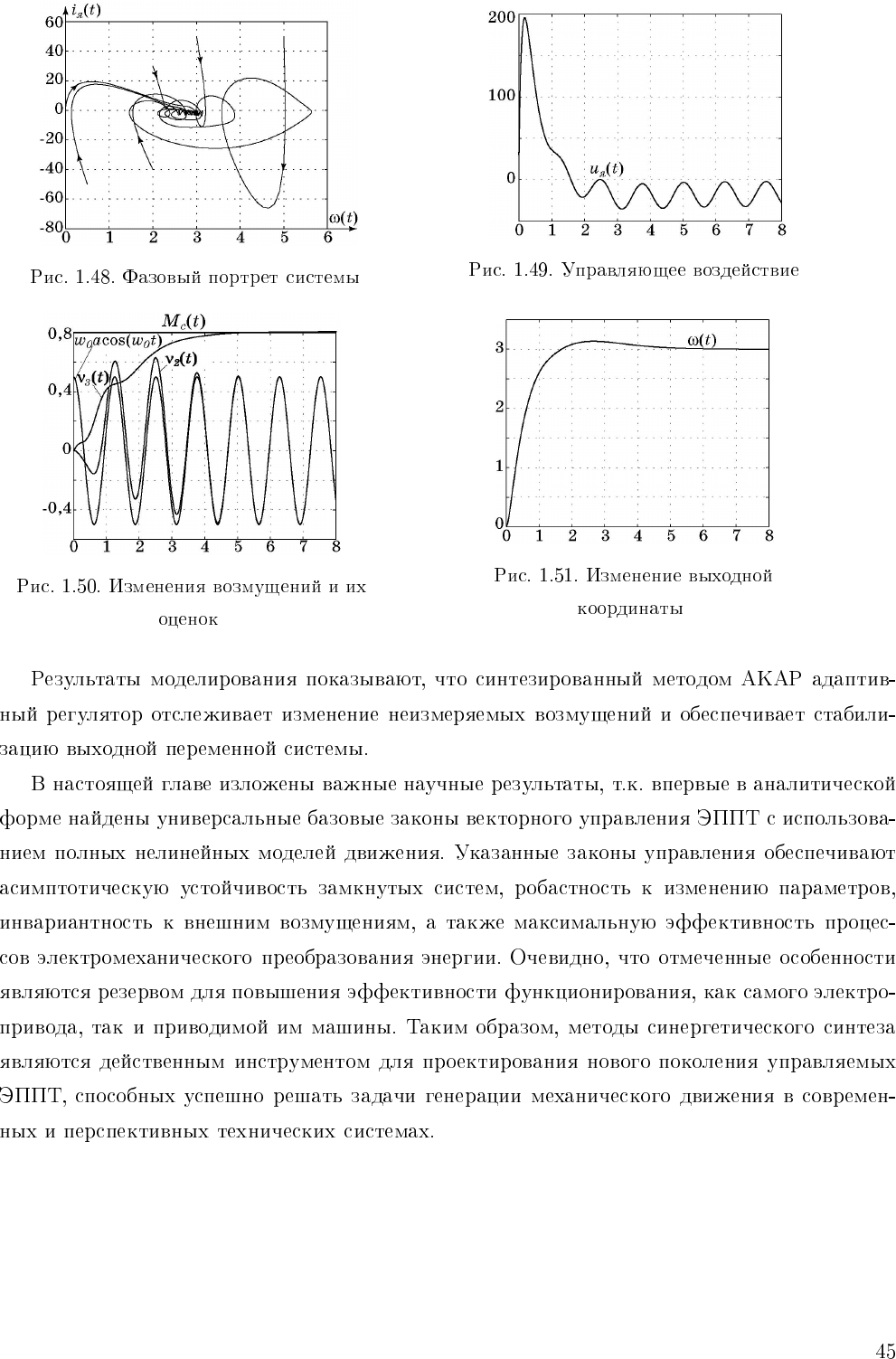


J
dω
r
dt
=
m
2
pk
r
ψ
r
i
sy
− M
c
;
dψ
r
dt
= r
r
k
r
i
sx
−
1
T
r
ψ
r
;
di
sy
dt
= −
1
T
∗
s
i
sy
− ω
ψ
i
sx
−
k
r
L
∗
s
ω
r
ψ
r
+
1
L
∗
s
u
sy
;
di
sx
dt
= −
1
T
∗
s
i
sx
+ ω
ψ
i
sy
+
k
r
T
r
L
∗
s
ψ
r
+
1
L
∗
s
u
sx
.
u
sx
u
sy
x y
i
sx
i
sy
ψ
r
ω
r
ω
ψ
k
r
=
L
m
Lr
r
s
r
r
L
s
L
r
L
m
L
∗
s
= L
s
− L
m
k
r
r
∗
s
= r
s
+ r
r
k
2
r
T
r
=
L
r
r
r
T
∗
s
=
L
∗
s
r
∗
s
p J
m M
c
ψ
r
(ω
ψ
− ω
r
)=k
r
r
r
i
sy
.
•
•
•
•
•
•
(α, β)
i
sα
=
2
3
(i
sa
−
1
2
i
sb
−
1
2
i
sc
);
i
sβ
=
1
√
2
(i
sb
− i
sc
).
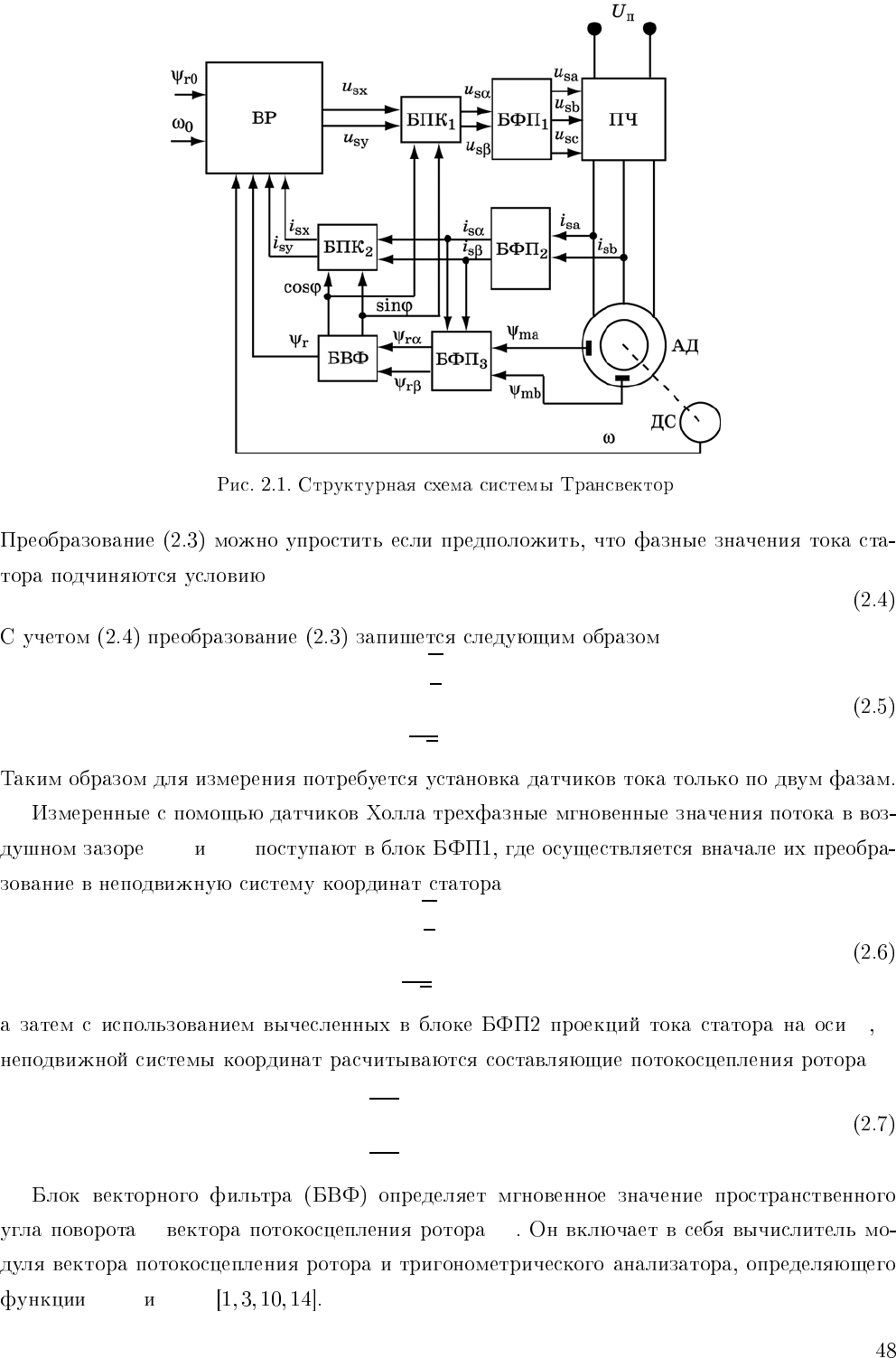
i
sa
+ i
sb
+ i
sc
=0.
i
sα
=
3
2
i
sa
;
i
sβ
=
1
√
2
(i
sa
+2i
sb
).
ψ
ma
ψ
mb
(α, β)
ψ
mα
=
3
2
ψ
ma
;
ψ
mβ
=
1
√
2
(ψ
ma
+2ψ
mb
),
α β
ψ
rα
=
L
r
L
m
ψ
mα
− (L
r
− L
m
)i
sα
;
ψ
rβ
=
L
r
L
m
ψ
mβ
− (L
r
− L
m
)i
sβ
.
ϕ ψ
r
sin ϕ cos ϕ

(α, β) (x, y)
i
sx
= i
sα
cos ϕ + i
sβ
sin ϕ;
i
sy
= −i
sα
sin ϕ + i
sβ
cos ϕ.
(x, y) (α, β)
u
sα
= u
sx
cos ϕ −u
sy
sin ϕ;
u
sβ
= u
sx
sin ϕ + u
sy
cos ϕ,
(α, β)
u
sa
=
2
3
u
sα
;
u
sb
=
2
3
(−
1
2
u
sα
+
√
3
2
u
sβ
);
u
sc
=
2
3
(−
1
2
u
sα
−
√
3
2
u
sβ
).
ψ
r
ω =
ω
r
p
ω
ψ
i
sy
; ω
ψ
i
sx
;
k
r
r
r
L
∗
s
L
r
ψ
r
.
k
r
L
∗
s
ω
r
ψ
r
dψ
r
dt
= r
r
k
r
i
sx
−
1
T
r
ψ
r
;
di
sx
dt
= −
1
T
∗
s
i
sx
+
1
L
∗
s
u
1
;
du
1
dt
=
1
T
(k ¯u
sx
− u
1
),
J
dω
r
dt
=
m
2
pk
r
ψ
r
i
sy
− M
c
;
di
sy
dt
= −
1
T
∗
s
i
sy
+
1
L
∗
s
u
2
;
du
2
dt
=
1
T
(k ¯u
sy
− u
2
),
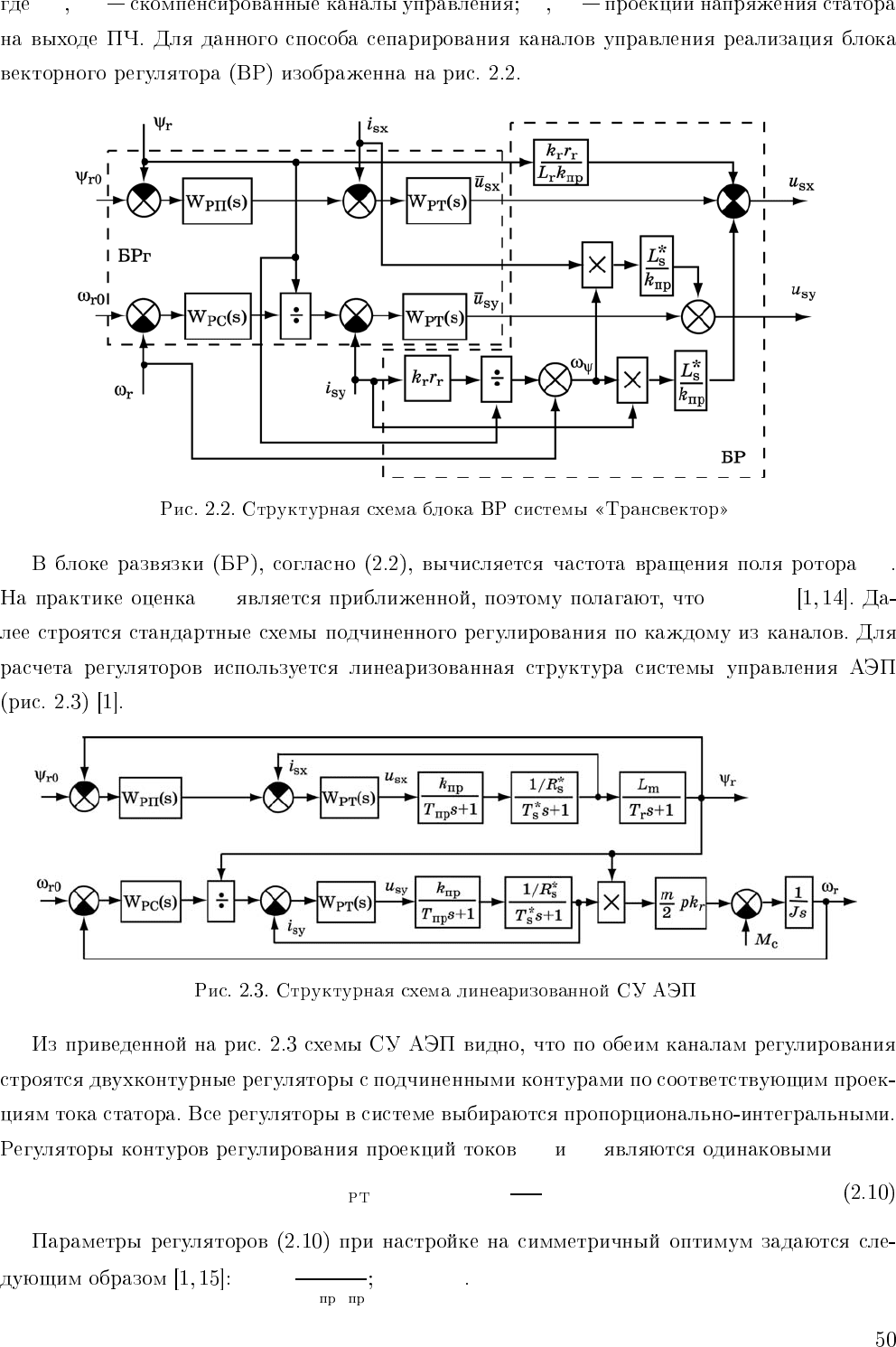
¯u
sx
¯u
sy
u
1
u
2
ω
ψ
ω
ψ
ω
ψ
≈ ω
r
i
sx
i
sy
W (s)=K
I
1+
1
T
I
s
.
K
I
=
L
∗
s
2T k
T
I
=4T
∗
s
