Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.


θ = θ
∗
=const
θ = θ
∗
Φ=Φ
∗
M
f
(t)=const
˙
θ(t)=ω;
˙ω(t)=(a
1
i Φ − M
c
(ω) − z
1
)a
2
;
˙
i
(t)=(u − a
1
Φω − a
3
i )a
4
;
˙
Φ(t)=(u
− a
5
f
1
(Φ))a
6
;
˙z
1
(t)=β(θ − θ
∗
).
ψ
1
= i − ϕ
1
(θ, ω, z
1
)=0;
ψ
2
=Φ− Φ
∗
=0.
˙
θ(t)=ω;
˙ω(t)=(a
1
ϕ
1
(θ, ω, z
1
)Φ
∗
− M
c
(ω) − z
1
)a
2
;
˙z
1
(t)=β(θ − θ
∗
).
ϕ
1
(θ, ω, z
1
)
ψ
3
= ω + b
1
(θ − θ
∗
)=0.

ψ
3
=0 ω = −b
1
(θ − θ
∗
)
˙
θ(t)=−b
1
(θ − θ
∗
);
˙z
1
(t)=β(θ − θ
∗
),
b
1
> 0 θ → θ
∗
˙z
1
(t) → 0
ψ
1
=0 ψ
2
=0 ψ
3
=0 θ = θ
∗
Φ=Φ
∗
ψ
1
=0
ϕ
1
(θ, ω, z
1
)=
1
a
1
Φ
∗
M
c
(ω)+z
1
−
1
a
2
T
3
((T
3
b
1
+1)ω+b
1
(θ−θ
∗
))
,
T
3
˙
ψ
3
(t)+ψ
3
=0,
ψ
1
=0
u = a
3
i +
1
T
1
a
4
1
a
1
Φ
∗
M
c
−
1
a
2
T
3
((T
3
b
1
+1)ω+b
1
(θ−θ
∗
))
−i
−
−
1
a
4
a
1
Φ
∗
b
1
a
2
T
3
ω−
a
2
∂M
c
∂ω
−
T
3
b
1
+1
T
3
(a
1
i Φ−M
c
)−β(θ−θ
∗
)
+
+
β
a
4
a
1
Φ
∗
T
1
1+T
1
a
2
∂M
c
∂ω
−
T
3
b
1
+1
T
3
(θ − θ
∗
)dt + a
1
ωΦ;
u
= a
5
f
1
(Φ) −
1
T
2
a
6
(Φ − Φ
∗
).
ψ
1
=0 ψ
2
=0
z
1
↔ M
f
(t)
θ
(t)+
b
1
+
1
T
3
¨
θ(t)+
1
T
3
˙
θ(t) − a
2
βθ + a
2
˙
M
f
(t)=−a
2
βθ
∗
.
θ = θ
∗
M
f
(t)=const b
1
+
1
T
3
> 0 β<0
θ
∗
=40π

ω = ω
∗
=const θ = θ
∗
=const
θ = θ
∗
(t)
θ
∗
(t)=A
1
t + A
max
sin(ω
1
t)
Φ=Φ
∗
M
f
(t)=const

y
1
= A
1
t y
2
= A
max
sin(ω
1
t) ˙y
1
(t)=A
1
y
2
˙y
2
(t)=(A
2
max
− y
2
2
− y
2
3
)y
2
+ ω
2
1
y
3
;
˙y
3
(t)=(A
2
max
− y
2
2
− y
2
3
)y
3
− ω
2
1
y
2
.
˙
θ(t)=ω;
˙ω(t)=(a
1
i Φ − M
c
(ω) − z
1
)a
2
;
˙
i
(t)=(u − a
1
Φω − a
3
i )a
4
;
˙
Φ(t)=(u
− a
5
f
1
(Φ))a
6
;
˙y
1
(t)=A
1
;
˙y
2
(t)=(A
2
max
− y
2
2
− y
2
3
)y
2
+ ω
2
1
y
3
;
˙y
3
(t)=(A
2
max
− y
2
2
− y
2
3
)y
3
− ω
2
1
y
2
.
˙z
1
(t)=β(θ − y
1
− y
2
).
ψ
1
= i − ϕ
1
(θ, ω, y
1
,y
2
,y
3
,z
1
)=0;
ψ
2
=Φ− Φ
∗
=0.
˙
θ(t)=ω;
˙ω(t)=(a
1
ϕ
1
(θ, ω, y
1
,y
2
,y
3
,z
1
)Φ
∗
− M
c
(ω) − z
1
)a
2
;
˙y
1
(t)=A
1
;
˙y
2
(t)=(A
2
max
− y
2
2
− y
2
3
)y
2
+ ω
2
1
y
3
;
˙y
3
(t)=(A
2
max
− y
2
2
− y
2
3
)y
3
− ω
2
1
y
2
.
˙z
1
(t)=β(θ − y
1
− y
2
).
ψ
3
= ω + b
1
(θ − y
1
− y
2
)=0.

˙
θ(t)=−b
1
(θ − y
1
− y
2
);
˙y
1
(t)=A
1
;
˙y
2
(t)=(A
2
max
− y
2
2
− y
2
3
)y
2
+ ω
2
1
y
3
;
˙y
3
(t)=(A
2
max
− y
2
2
− y
2
3
)y
3
− ω
2
1
y
2
.
˙z
1
(t)=β(θ − y
1
− y
2
).
T
i
˙
ψ
i
(t)+ψ
i
=0,i=1,...,3.
u = a
3
i +a
1
ωΦ−
1
a
4
∂ϕ
1
∂θ
ω+β
∂ϕ
1
∂z
1
(θ−y
1
−y
2
)dt+
∂ϕ
1
∂y
1
A
1
−
−
1
a
4
∂ϕ
1
∂ω
(a
1
i Φ − M
c
− β(θ − y
1
− y
2
))−
−
1
a
4
∂ϕ
1
∂y
2
((A
2
max
− y
2
2
− y
2
3
)y
2
+ ω
2
1
y
3
)−
−
1
a
4
∂ϕ
1
∂y
3
((A
2
max
− y
2
2
− y
2
3
)y
3
+ ω
2
1
y
2
) −
1
a
4
T
1
(i + ϕ
1
);
u
= a
5
f
1
(Φ) −
1
T
2
a
6
(Φ − Φ
∗
),
ϕ
1
=
1
a
1
Φ
∗
M
c
+ z
1
−
b
1
a
2
(ω − A
1
− (A
2
max
− y
2
2
− y
2
3
)y
2
− ω
2
1
y
3
)
−
(ω + b
1
(θ − y
1
− y
2
))
a
1
Φ
∗
T
3
z
1
y
1
y
2
y
3
A
1
=0, 5 A
2
=3 ω
1
=1
(A
1
=0)
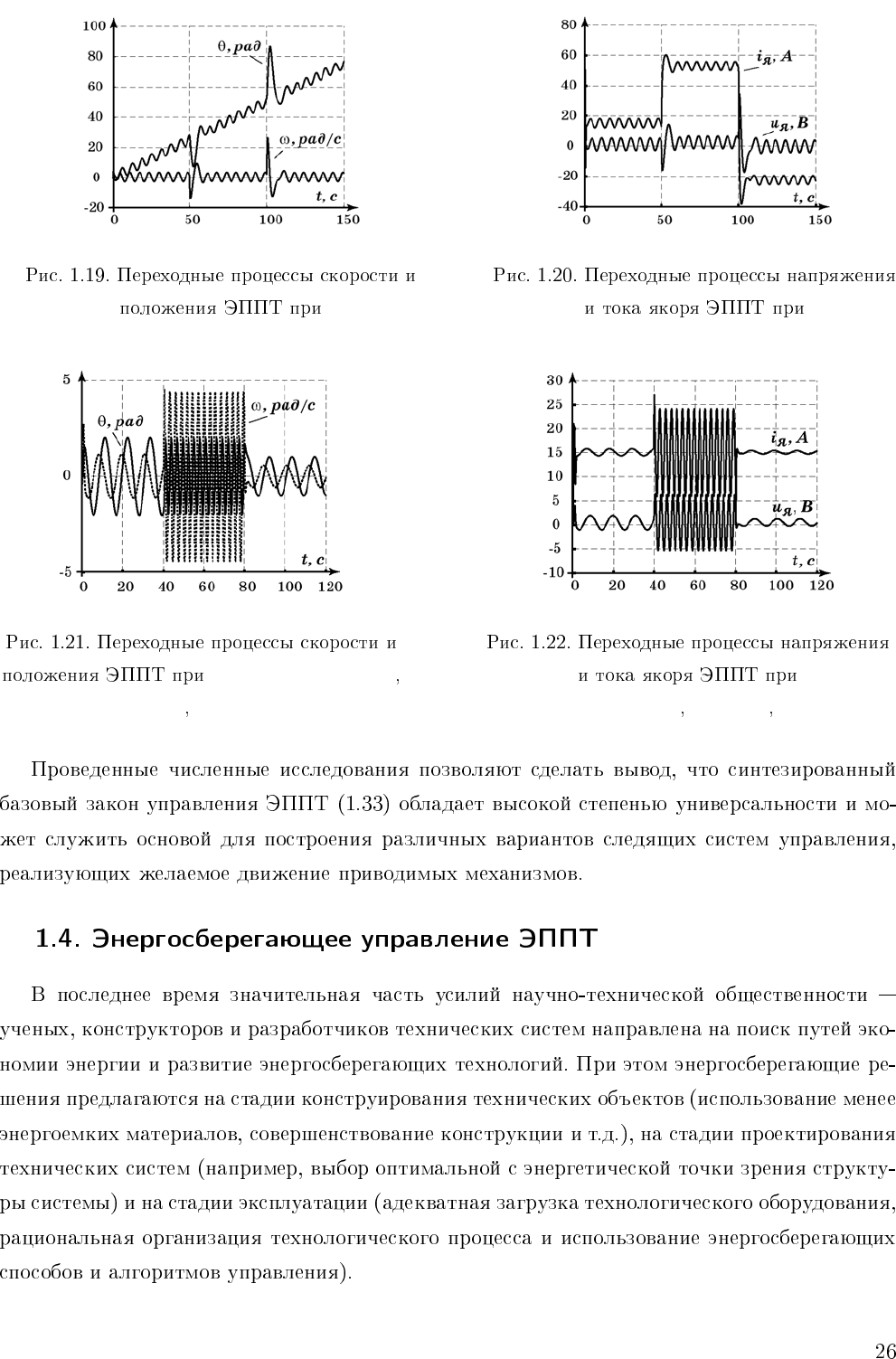
θ
∗
(t)=A
1
t + A
max
sin(ω
1
t) θ
∗
(t)=A
1
t + A
max
sin(ω
1
t)
θ
∗
(t)=A
max
sin(ω
1
t)
ω
1
= var A
max
=var θ
∗
(t)=A
max
sin(ω
1
t) ω
1
= var A
max
=var


∂∆P
Σ
∂x
=0

∆P =∆P +∆P = i
2
r + i
2
r +∆P
f
50
β
Φ
Φ
2
.
∆P Φ
f β
Φ(i )

i = k
Φ
Φ
i =
M
Σ
cΦ
∆P (Φ) =
M
2
Σ
r
c
2
Φ
2
+ k
2
Φ
Φ
2
r +∆P
ω
314
β
Φ
Φ
2
.
∂∆P
∂Φ
=0⇐⇒ −
M
2
Σ
r
c
2
Φ
3
+ k
2
Φ
Φr +
∆P
ω
β
314
β
Φ
2
Φ=0.
Φ = M
1
2
Σ
k
1
k
2
+ k
3
ω
β
1
4
.
k
1
=
r
c
2
; k
2
= r k
2
Φ
; k
3
=
∆P
314
β
Φ
2
.
