Колесников А.А. Синергетические методы управления сложными системами: механические и электромеханические системы
Подождите немного. Документ загружается.

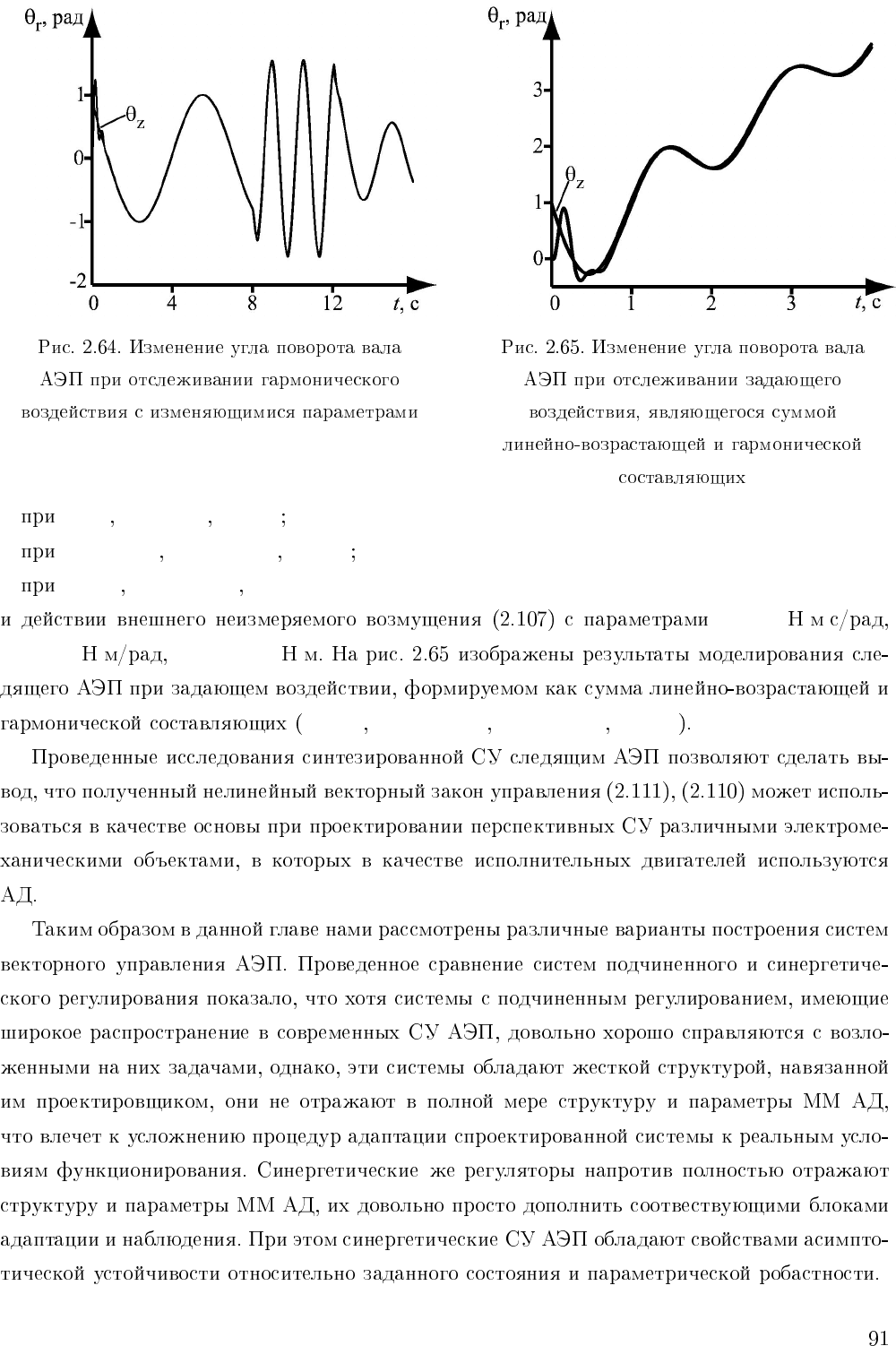
• t<8 A
max
=1 ω
0
=1
• 8 t<12 A
max
=1, 5 ω
0
=2
• t 12 A
max
=0, 5 ω
0
=1, 5
µ =1 · ·
ρ = 100 · M
c0
= 200 ·
α
0
=0 α
1
= α
2
=1 A
max
=0, 1 ω
0
=2



¨x(t)+f(x)=u.
¨x(t) − b sin x = u
0
sin x,
u
0
˙x
1
(t)=x
2
;
˙x
2
(t)=−f(x
1
)+u.
u
ψ
u =0
E
0
=0, 5x
2
2
+ F (x
1
)=const, F (x
1
)=
x
1
0
f(ξ)dξ.
x
2
=˙x
1
(t)=±
2(E
0
− F (x
1
)).
u =0
E
0
¨x(t)+ω
2
0
x =0
˙x
1
(t)=±ω
0
2E
0
ω
2
0
− x
2
1
.

x
1
(t)=
√
2E
0
ω
0
sin(ω
0
t + ϕ
0
)=a sin(ω
0
t + ϕ
0
),
a =
√
2E
0
ω
0
=
1
ω
0
x
2
20
+ ω
2
0
x
2
10
ϕ
0
= arctg
x
20
ω
0
x
10
ψ
ψ
ψ
1
=
0, 5x
2
2
+ F (x
1
)
˙
ψ
1
(t)=αψ
1
(A
1
− ψ
1
)x
2
2
,
ψ
1
(t)
ψ
1s
= A
1
ψ
1
u
1
=2αψ
2
1
(A
1
− ψ
1
)x
2
=2αψ
1
(A
1
− ψ
1
)
0, 5x
2
2
+ F (x
1
)x
2
.
ψ
1
= A
1
x
2
=˙x
1
(t)=±
2(A
2
1
− F (x
1
)),
ψ
1
= A
1
u
1ψ
=0 ψ
1
E
0
=0, 5x
2
2
+ F (x
1
)=ψ
2
1s
= A
2
1
ψ
1
= A
1
ψ
2
ψ
2
=
0, 5x
2
2
+ F (x
1
) − A
2
T
2
˙
ψ
2
(t)+x
2
2
ψ
2
=0,
3T
2
ψ
2
=0 ψ
2
u
2
= −
2ψ
2
x
2
0, 5x
2
2
+ F (x
1
)
T
2
,
u
1
ψ
2
=0
ψ
2
=0

E
0
= A
2
2
ψ
2
=0
x
2
=˙x
1
(t)=±
2(A
2
2
− F (x
1
)),
ψ
3
=0, 5x
2
2
+ F (x
1
) − E
0
,
E
0
ψ
3
E
0
E
0
=0
T
3
˙
ψ
3
(t)+x
2
2
ψ
3
=0
u
3
= −
x
2
T
3
ψ
3
,
u
1
u
2
ψ
3
=0
ψ
3
=0 E
0
ψ
3
=0
˙x
1
(t)=x
2ψ
= ±
2
E
0
− F (x
1ψ
)
.
ψ
1
=0 ψ
2
=0 ψ
3
=0

˙
θ(t)=ω;˙ω(t)=M +(ν + µ sin ωt)sinθ,
θ M ν µ
M =0 sin θ ≈ θ

M =0 ν = g µ = aω
2
¨
θ(t)+(g + aω
2
sin ωt)sinθ =0,
J
¨
θ(t) − ml(g + aω
2
sin ωt)sinθ =0,
θ J m
l g
u = F (θ,
˙
θ)
u(t)
u(t)
x
1
= θ x
2
=
˙
θ(t)
˙x
1
(t)=x
2
,
˙x
2
(t)=
ml
J
(g + u)sinx
1
.
u(x
1
,x
2
)
x
1
= x
2
=0
ψ
1
= x
2
− ω
A
2
− x
2
1
,
ψ
1

T
1
˙
ψ
1
(t)+x
2
1
ψ
1
=0,
˙x
2
(t)+
ωx
1
˙x
1
(t)
A
2
− x
2
1
+
x
2
1
T
1
ψ
1
=0,
mlu
1
J
= −
ωx
1
x
2
A
2
− x
2
1
sin x
1
−
x
2
1
ψ
1
T
1
sin x
1
−
mlg
J
.
˙x
1
(t)=x
2
,
˙x
2
(t)=−
ωx
1
x
2
A
2
− x
2
1
−
x
2
1
ψ
1
T
1
.
ψ
1
=0
dx
2
dx
1
= −
ωx
1
A
2
− x
2
1
−
x
2
1
ψ
1
T
1
x
2
.
ψ
1
=0
x
2
= ω
A
2
− x
2
1
,
ψ
1
=0
ψ
1
=0 u
1
x
1
x
2
x
1
ψ
1
˙x
1
(t)=ω
A
2
− x
2
1
+ ψ
1
,
˙
ψ
1
(t)=−
x
2
1
T
1
ψ
1
.
¨x
1
(t)=−ω
2
x
1
−
ωx
1
A
2
− x
2
1
+
x
2
1
T
1
ψ
1
,
˙
ψ
1
(t)=−
x
2
1
T
1
ψ
1
.
t
n
=(3÷ 4)T
1
x
1
(t)=A sin(ωt + ϕ
0
),x
2
(t)=Aω sin(ωt + ϕ
0
).
ψ
1
=0

ψ
1
=0
˙x
1ψ
(t)=ω
A
2
− x
2
1ψ
,
˙x
2
1ψ
+ ω
2
x
2
1ψ
= ω
2
A
2
=2E
0
,
E
0
ψ
1
=0
ω A ψ
1
=0
mlu
1ψ
J
= −
ω
2
x
1ψ
sin x
1ψ
−
mlg
J
,
¨x
1ψ
(t)+ω
2
x
1ψ
=0,
ψ
1
=0
ψ
1
=0
x
1ψ
(t)=a sin(ωt + ϕ
0
),
a =
1
ω
˙x
2
10ψ
+ ω
2
x
10ψ
; ϕ
0
= arctg
˙x
10ψ
ωx
10
.
ψ
1
=0
u
1
˙x
10ψ
x
20ψ
x
10ψ
x
20ψ
=˙x
10ψ
= ω
A
2
− x
2
10ψ
,
a = A ϕ
0
= arctg
⎛
⎝
A
2
− x
2
10ψ
˙x
10
⎞
⎠
=arcsin
x
10ψ
A
.
ψ =0
