Кочарян Г.Г. Деформационные процессы в массивах горных пород

Подождите немного. Документ загружается.

251

где

H =

Таким образом, приливообразующая сила пропорциональна массе

возмущающего тела и обратно пропорциональна третьей степени

расстояния до возмущающего тела. Поэтому приливообразующая

сила Луны оказывается больше, чем приливообразующая сила

Солнца.

Из (6.5) следует, что свободная поверхность жидкости имеет

форму эллипсоида вращения, осью которого является прямая линия,

соединяющая центры Земли и притягивающего тела. При этом

точке пересечения этой линии с поверхностью Земли

(

= и0

) высота прилива будет наибольшей Hh

= . В

этих точках притягивающее тело (Луна или Солнце) находится в

зените или надире. В точках, для которых притягивающее тело

находится на горизонте (

−=

, это максимальный

отлив. Для Луны имеем:

3.60

;

, a=6370км, т.е

согласно (6.5)

H=54см. Аналогично для Солнца:

40023

;000333 ==

, H=25см.

Таким образом, приливообразующее действие Луны в два раза

сильнее такого же действия Солнца.

И приливообразующая сила, и высота прилива зависят от

расстояния от Земли до притягивающего тела, которое периодически

изменяется. Так зенитное расстояние Луны меняется периодически в

течение лунных суток (равных 24 часам 50 минутам), и в течение

лунного месяца (равного 29,5

суткам). Поэтому Лунные приливы

обладают как суточной, так и месячной периодичностью. В течение

месяца расстояние от Луны до Земли изменяется приблизительно от

r =356 тыс. км до r=406 тыс. км, а приливообразующая сила

изменяется примерно в 1,4 раза. Высота Луны над горизонтом в

252

момент кульминации изменяется за месяц в среднем на 47°, причем

амплитуда изменений колеблется с периодом около 19 лет от 37 до

57°; это приводит к месячным колебаниям высоты приливов и

отливов и к колебаниям с периодом около 19 лет.

Если учесть при оценке высоты прилива координаты Луны

(склонение δ и часовой угол α, отсчитываемый к

западу от

меридиана

, проходящего через точку измерений и полюс Земли), то

можно получить следующие выражения для высоты приливов:

⎥

⎦

⎤

⎢

⎣

⎡

−−

αδϕ

αϕδ

ϕδ

2coscoscos

cos2sin2sin

)sin31)(sin31(

Hh ,

или

321

hhhh

, где

⎪

⎩

⎪

⎨

⎧

−−=

αδϕ

αϕδ

ϕδ

2coscoscos

cos2sin2sin

)sin31)(sin31(

(6.6)

Слагаемое

зависит только от широты места наблюдения

от склонения Луны

и не зависит от часового угла Луны α.

Периодичность изменения величины

- лунный месяц.

Соответственно, период изменения

в два раза меньше (т.к. в h

входит sin

). Поэтому h

представляет высоту полумесячного

лунного прилива. Эти приливы обращаются в нуль на широте

6135

′

, для которой

sin =

и имеют наибольшее значение

на полюсе.

Выражение для h

содержит

cos

. При этом α изменяется на

360° в течение лунных суток, в то время как

за этот промежуток

253

времени изменяется мало. Поэтому h

представляет высоту

суточного прилива. В северном полушарии ( 00 >>

и ),

наибольшая высота суточного прилива будет при

1cos =

, т. е.

при прохождении Луны через меридиан точки наблюдения, а

наименьшая при

1cos

−

, т. е. при прохождении Луны через

меридиан - антипод. Суточный прилив имеет наибольшую

величину на широте

45=

и обращается в нуль на экваторе

(

) и на полюсе (

90=

Третье слагаемое h

представляет высоту прилива с

полусуточным периодом, поскольку период изменения

множителя

2cos

является половина лунных суток. Наибольшая

высота полусуточного прилива, обычно наиболее заметного, будет

при

12cos =

, т. е. при

или

180=

. Эти значения угла α

отвечают, очевидно, прохождению Луны через меридиан точки

наблюдения

Q над горизонтом или под ним. Наименьшая высота

полусуточного прилива будет при

12cos

−

, т. е. при

или 27090 ==

αα

Явление полусуточного прилива интенсивнее всего протекает

на экваторе (где

), а также в те дни, когда Луна проходит через

экватор (

). На полюсе (

90=

) полусуточный прилив

отсутствует.

Аналогичные рассуждения можно применить и для солнечных

приливов.

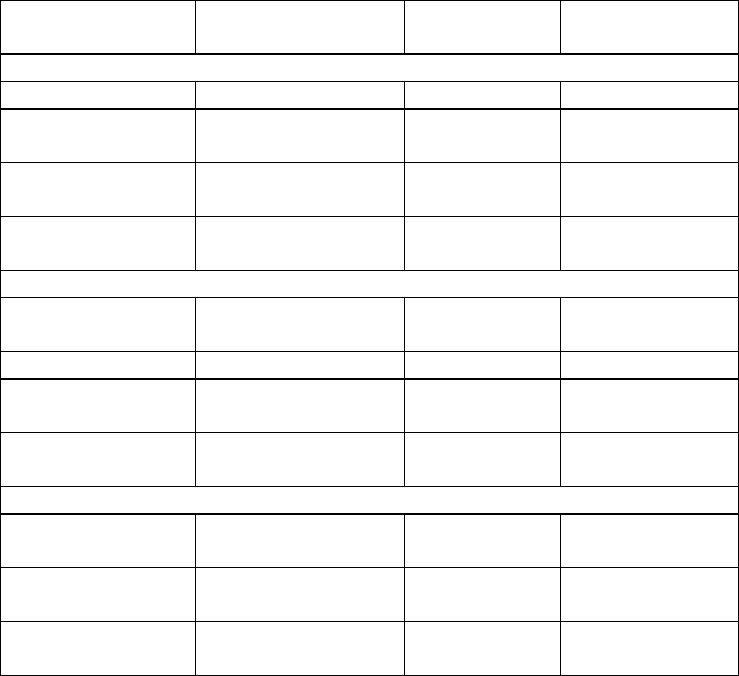
В таблице 6.1 приведены параметры основных лунных и

солнечных приливов.

254

Таблица 6.1 Периоды и относительная амплитуда основных

приливов.

Обозначение

прилива

Название прилива

Период, ч

Амплитуда %

Полусуточные приливы

Главный Лунный 12.421 100

Главный

Солнечный

12.000 46.564

Эллиптический

Лунный

12.568 19.156

Смешанный

Лунно-Солнечный

11.967 12.670

Суточные приливы

Смешанный

Лунно-Солнечный

23.935 58.417

Главный Лунный 25.819 41.502

Главный

Солнечный

24.066 19.330

Эллиптический

Лунный

26.868 7.916

Долгопериодические приливы

Двухнедельный

Лунный

13.661 17.225

Месячный

Лунный

27.555 9.084

Полугодовой

Лунный

182.621 8.024

Суперпозиция разнообразных лунных и солнечных приливных

волн создает очень сложную картину. Когда Солнце и Луна

находятся на одной прямой с Землей (то есть в полнолуние и

новолуние), приливы получаются особенно сильными. Их называют

большими или сизигийными (рис.6.2а). Когда Луна находится в

первой и в последней четверти, лунные приливы ослабляются

из-за

наложения солнечных. В таких случаях говорят о малых, или

квадратурных, приливах (рис.6.2б).

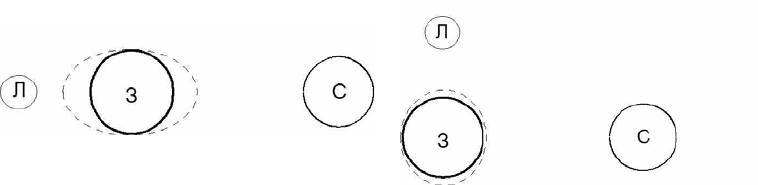
255

Рис.6.2 Схема образования сигзигийных (а) и квадратурных (б)

приливов

Амплитуды больших приливов могут быть в 2,7 раза

больше амплитуды малых.

6.1.2 Приливы в твердой Земле

Под действием приливообразующих сил деформируется не

только водная оболочка, но и все тело Земли. При прохождении

упругих приливных волн вертикальные смещения земной

поверхности могут достигать 50

см (при положениях Луны и Солнца

в зените или надире), а горизонтальные — 5

см. Приливные

изменения силы тяжести на экваторе достигают 0,25

мгал,

изменения отвесной линии — 0,01’’, а изменения наклонов земной

поверхности, т. е. угла между поверхностью земли и отвесом, —

0,02’’, приливные деформации поверхностных слоев Земли —

порядка 10

-8

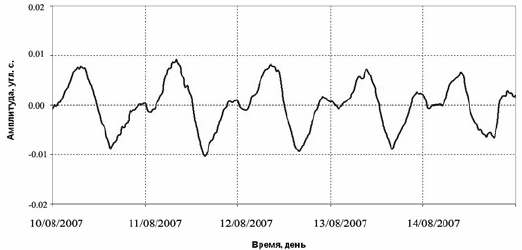
Приливные деформации твердой Земли регистрируются

инструментально различными приборами: гравиметрами,

наклономерами, длиннобазовыми деформографами. На рис.6.3

показан пример записи приливных деформаций.

Расчет амплитуд и фаз приливных деформаций твердой

Земли представляет довольно сложную задачу. Основополагающая

работа по связи возмущающей силы с деформацией была сделана

А.Лявом. Согласно теории Лява; деформация, обусловленная

возмущающим приливным

потенциалом V, описывается той же

256

сферической гармоникой второго порядка, умноженной на

комбинацию числовых коэффициентов, называемых числами Лява:

h - коэффициент изменения радиуса (отношения высоты земного

прилива к соответствующей высоте статического океанского

прилива на абсолютно жесткой Земле);

f - коэффициент изменения

объема (отношения объемного расширения к высоте

соответствующего статического прилива);

к - коэффициент

изменения плотности (отношения дополнительного потенциала из-за

деформации к потенциалу прилива);

l - коэффициент,

характеризующий изменение наклона отвеса из-за лунно-солнечного

прилива, называемый числом Шида.

Рис.6.3. Пример горизонтальной (С-Ю) приливной компоненты,

зарегистрированной высокоточным наклономером

В настоящее время для расчета амплитуды и фазы

приливных деформаций обычно используют стандартные

программы расчета, например ETERNA 3.0 [http://www.geo.uni-

jena.de/geophysik/etc/etcdat/].

При анализе результатов инструментальных наблюдений

приливных деформаций обычно ограничиваются параметрами

основных волн: полусуточных

и S

и суточных K

и О

— суточной.

Существенным образом приливные деформации сказываются

и на динамике пластов, содержащих флюиды. Хотя положение

уровня флюида в скважине определяется, прежде всего, геометрией

257

пласта и величиной порового давления, существуют факторы

второго порядка, на которые система пласт-скважина реагируют

достаточно чутко. К таким факторам относится, в том числе, и

деформирование коллектора приливными силами.

Изменение положения уровня флюида в скважине под

воздействием внешних факторов называют

откликом уровня.

Отклик уровня очень сильно зависит от условий залегания пласта.

Различают два идеализированных случая -

пласт, ограниченный

водоупором; напорный пласт (confined aquifer) и неограниченный

или безнапорный пласт

(unconfined aquifer).

случ

ае

напо

рног

плас

та,

идеа

лизи

рова

нная

сист

ема

сост

оит

из

про

ницаемой пористой среды - пласта, ограниченного сверху и снизу

непроницаемым материалом. Обычно размер пласта в

горизонтальном направлении настолько велик, что его можно

считать бесконечным.

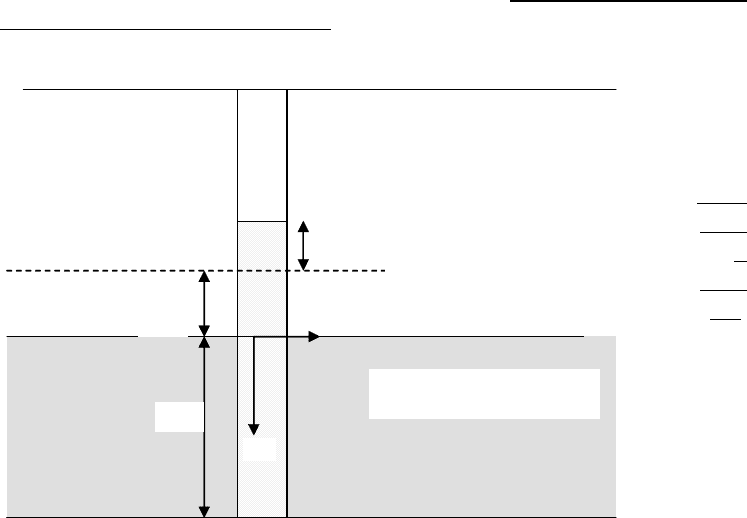
Жидкость в напорном пласте находится под определенным

давлением так, что уровень флюида в скважине, пробуренной в

напорном пласте, обычно выше

кровли пласта. Этот уровень

Начальная пьезометрическая

пове

хность

Пласт, ограниченный

водо

по

ными слоями

Рис.6.4 Схема напорного пласта

258

называют пьезометрической поверхностью. Ее положение

определяется, очевидно, давлением

p жидкости в пласте на уровне

кровли:

(6.7)

Поровое давление меняется по высоте пласта :

)( zhgp

(6.8)

(ось z направлена вниз).

При деформации пласта часто полагают, что изменение

объема твердого скелета мало по сравнению с изменением объема

пор и расположенной в них жидкости. Это приближение чаще всего

выполняется в пластах, состоящих из гранулированного материала

типа песка, однако не всегда справедливо для более плотных

коллекторов типа известняков. Если это

предположение

выполняется, то практически все изменение объема при

деформировании приходится на долю изменения жидкости в порах.

Соответственно, изменение гидравлического напора при

заданной объемной деформации

zzyyxxkk

(6.9)

составляет:

ρρρ

/⋅Δ

⋅

=−=−

, (6.10)

где E

= 2.3 10

Па – объемный модуль упругости воды, а n –

пористость.

259

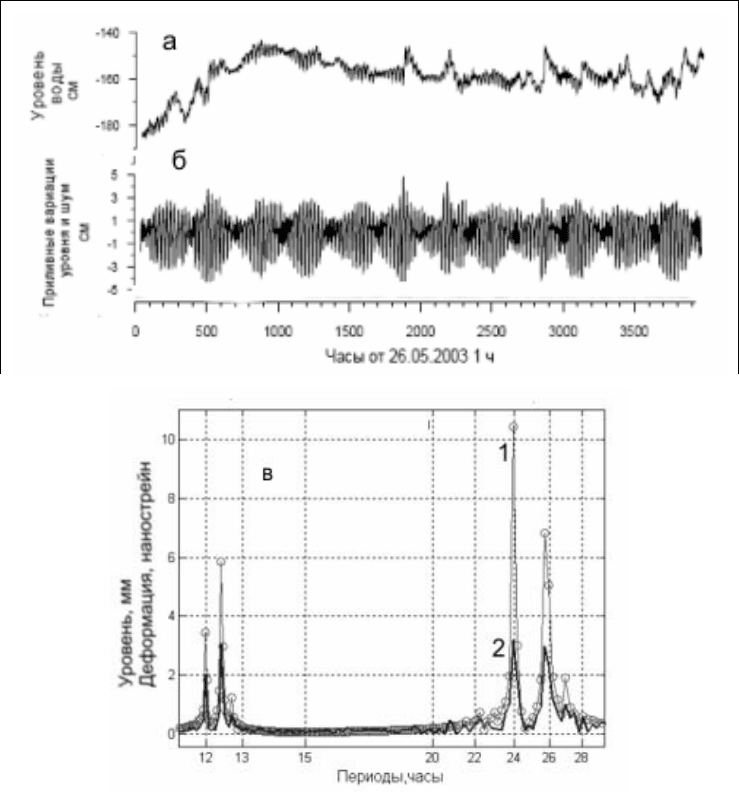
Рис.6.5 (а) Запись изменения уровня воды в скважине со

временем, (б) выделенные в результате фильтрации

первоначальной записи приливные вариации, (в) спектры

приливной деформации (1) и уровня (2)

260

Как видно, в этом идеализированном случае динамика уровня

зависит, главным образом, от пористости коллектора – чем ниже

пористость, тем сильнее реакция системы скважина-пласт на

приложенную деформацию.

Если диаметр скважины считать бесконечно малым, то

изменение уровня жидкости в скважине

dH равно изменению

гидравлического напора в пласте

dh. При конечном диаметре

скважины необходимо учитывать влияние инерции при перетоке

жидкости из пласта в скважину и обратно.

Таким образом, в соответствии с (6.10), при объемной

деформации Δ~10

-8

, соответствующей приливным деформациям, и

пористости коллектора 20%, можно ожидать сантиметрового

изменения уровня флюида в скважине:

смdh 1.1

1010

2.0/310.210

⋅

−

В породах, где преобладает трещинная пористость,

чувствительность уровня к деформациям может быть выше, чем в

пористых средах. Она, кроме того, зависит от жесткости трещин.

Экспериментально определенные чувствительности трещиноватых

пластов к приливному воздействию достигают величины ~2см/10

-8

Пример записи уровня воды в скважине, вскрывшей напорный пласт

известняка, показан на рис.6.5. Здесь же показаны спектры

приливной деформации и уровня. Можно видеть, что спектральные

пики соответствуют периодам основных приливных волн.

В случае, когда пласт ограничен водоупором только снизу

(рис.6.6), поверхность флюида можно рассматривать как свободную.

Это означает, что изменение

высоты уровня жидкости обусловлено

лишь изменением объема пор под действием приложенных

напряжений и связано с деформацией пласта следующим образом:

=− , (6.11)

т.е. при тех же параметрах, как и в оценке для напорного пласта

(Δ~10

-8

, n ~20%) и толщине пласта 100м, получаем: