Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.

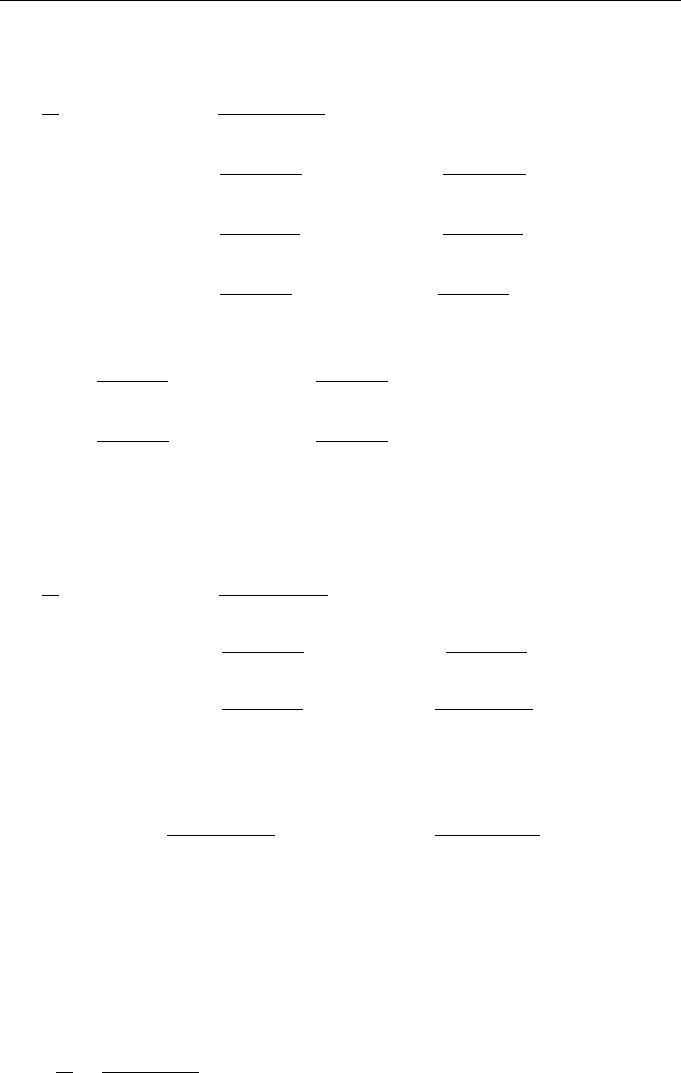
316 Lectures on Dynamics of Stochastic Systems
To derive an equation for this quantity, we differentiate Eq. (11.112) with respect
to r
s
and set r = 0. The result is the equation for the one-point correlation
∂
∂t
W
kp;js
(0;t)
= −2
∂
4
B
kp
(0)
∂r
n
∂r
m
∂r
j
∂r
s
h
W
nm
(0;t)
i
− 2
∂
3
B
kp
(0)
∂r
n
∂r
m
∂r
j
W
nm;s
(0;t)
− 2
∂
3
B
kp
(0)
∂r
n
∂r
m
∂r
s
W
nm;j
(0;t)
+ 2
∂
3
B
kn
(0)
∂r
m
∂r
j
∂r
s
W
mp;n
(0;t)
+ 2
∂
3
B
np
(0)
∂r
m
∂r
j
∂r
s
W
km;n
(0;t)
− 2
∂
2
B
kp
(0)
∂r
n
∂r
m
W
nm;js
(0;t)
+ 2
∂
2
B
kn
(0)
∂r
m
∂r
j
W
mp;ns
(0;t)
+ 2
∂
2
B
kn
(0)
∂r
m
∂r
s
W
mp;jn
(0;t)
+ 2
∂
2
B
np
(0)
∂r
m
∂r
j
W
km;ns
(0;t)
+ 2
∂
2
B
np
(0)
∂r
m
∂r
s
W
km;jn
(0;t)
− 2
∂
2
B
qn
(0)
∂r
j
∂r
s
W
kp;qn
(0;t)
.
Convolve all functions with respect to indices k = p and j = s and take into account
Eq. (4.57), page 107, for the noncompressible flow of liquid. As a result, we arrive at
the equation of the form
∂
∂t
W
kk;ss
(0;t)
= −2
∂
4
B
kk
(0)
∂r
n
∂r
m
∂r
s
∂r
s
h
W
nm
(0;t)
i
− 4
∂
3
B
kk
(0)
∂r
n
∂r
m
∂r
s
W
nm;s
(0;t)
+ 2
∂
3
B
kn
(0)
∂r
m
∂r
s
∂r
s
W
mk;n
(0;t)
+ 2
∂
3
B
nk
(0)
∂r
m
∂r
s
∂r
s
W
km;n
(0;t)
+
4
(
d + 1
)
D
s
(d + 2)
W
mm;ss
(0;t)
.
Now, we content ourselves with excitation sources increasing exponentially in
time,
−2
∂
4
B
kk
(0)
∂r
n
∂r
m
∂r
s
∂r
s
h
W
nm
(0;t)
i
0
= −2
∂
4
B
kk
(0)
∂r
n
∂r
n
∂r
s
∂r
s
h
E(t)
i
0
−2
∞
Z
0
dτ
h
[
1u(r, t + τ )
] [
1u(r, t)
]
ih
E(t)
i
0
= −2D
(4)
H
h
E(t)
i
0
,
where D
(4)
H
=
R
dk k
4
E
s
(k).
Consider now the terms related to helicity (they are nonzero only in the three-
dimensional case). Using Eqs. (11.115) and (1.54), we obtain the equation of the form
∂
∂t
−
4
(
d + 1
)
D
s
(d + 2)
W
kk;ss
(0;t)
= −2D
(4)
H
h
E(t)
i
0
− 4800(d − 2)α
2
h
E(t)
i
0
t,
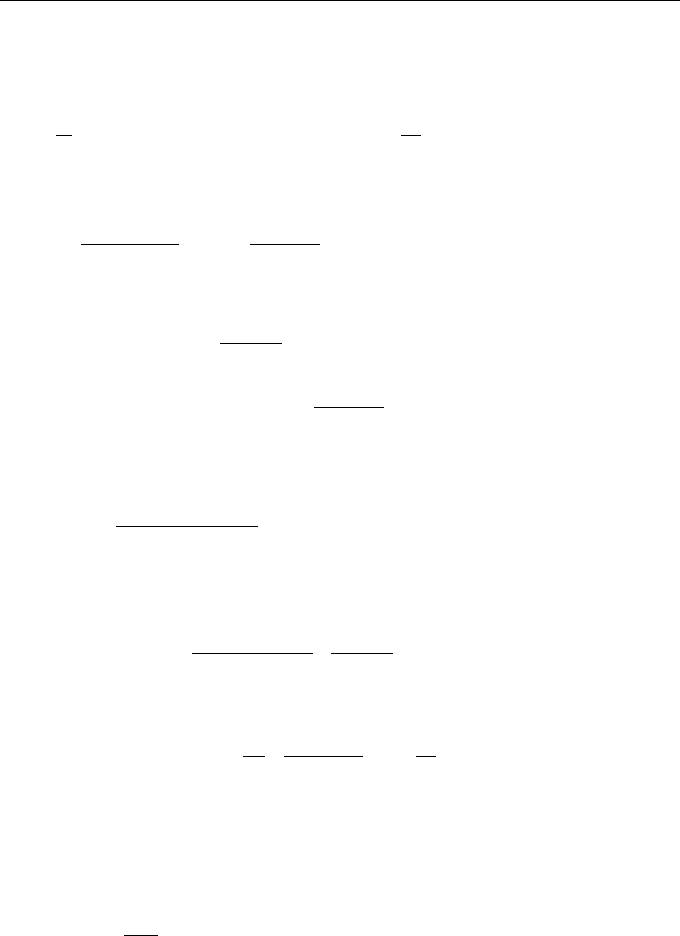
Passive Tracer Clustering and Diffusion 317
where we introduced factor (d −2) in the last term to emphasize that it vanishes in the
two-dimensional case. In accordance with Eq. (11.108), we can rewrite this equation
in terms of dissipation D
0
(t),
∂
∂t
− A
D
0
(t) =
2D
(4)
H
+ 4800(d − 2)α
2
∂
∂g
E
0
e
gt
, (11.117)
where
A =
4
(
d + 1
)
D
s
(d + 2)
, g =
2(d − 1)
d
D
s
.
Integrating Eq. (11.117), we obtain the expression for dissipation
D
0
(t) = 2D
(4)
H
h
E(t)
i
0
1
(
A − g
)
h
e
(
A−g
)
t
− 1
i
+ 4800(d − 2)α
2
h
E(t)
i
0
1
(
A − g
)
2
h
e
(
A−g
)
t
− 1 −
(
A − g
)
t
i
,
where positive parameter
A − g =
2
d
2
+ d + 2
D
s
d(d + 2)
.
Retaining here only increasing exponents, we obtain the final expression for temporal
evolution of dissipation,
D
0
(t) ≈
2D
(4)
H
+
4800(d − 2)α
2
(
A − g
)
h
E(t)
i
0
(
A − g
)
e
(
A−g
)
t
. (11.118)
In the three-dimensional case d = 3 and, hence,
D
(3)
0
(t) ≈
2D
(4)
H
+ 2571
α
2
D
s
15
h
E(t)
i
0
28D
s
exp
28
15
D
s
t
, (11.119)
The structure of the three-dimensional solution shows that dissipation of magnetic
field for great times is determined by helicity of the velocity field and average mag-
netic field energy (11.110) in absence of helicity.
In the two-dimensional case d = 2, helicity is absent and, consequently,
D
(2)
0
(t) ≈
D
(4)
H
D
s
h
E(t)
i
0
e
D
s
t
. (11.120)
In this case, energy dissipation is determined only by average energy.
As may be seen from Eqs. (11.119) and (11.120), dissipation increases in time much
faster than average energy does.
Now, we turn back to the original problem on dynamics of average energy subject
to dissipation. Substituting Eq (11.118) in Eq. (11.109) and integrating over time, we

318 Lectures on Dynamics of Stochastic Systems
obtain the solution to the problem in the form
h
E(t)
i
1
= E
0
exp
2(d − 1)D
s
d
t − 4µ
H
D
(4)
H
+
2400(d − 2)α
2
(
A − g
)
×
1
(
A − g
)
2
h
e
(
A−g
)
t
− 1
i
.
As may be seen from this formula, average energy decays very rapidly for t → ∞.
Maximum value of average energy is achieved at instant
D
s
t
max
≈
1
(
A − g
)
ln
(d − 1)
(
A − g
)
2
D
s
2dµ
H
h
D
(4)
H
(
A − g
)
+ 2400(d − 2)α
2
i
. (11.121)
In the three-dimensional case, we have
D
s
t
max
= −
15
28
ln µ
H
"
1, 6D
(4)
H
[
D
s
]
2
+
2066a
2
[
D
s
]
3
#
∼
∼
1
2
ln
σ
2
τ
0
µ
H
− 3, 8 in the presence of helicity,
1
2
ln
σ
2
τ
0
2µ
H
in the absence of helicity,
i.e., average energy reaches the maximum in the presence of helicity much faster than
in the absence of helicity.
In the two-dimensional case of plane-parallel flow of a liquid, we have
D
s
t
max
=
1
2
ln
[
D
s
]
2
2µ
H
D
(4)
H
∼
1
2
ln
σ
2
τ
0
2µ
H
.
Applicability condition of the neglect of the effect of dynamic diffusion is, evi-
dently, the condition
t t
max
.
Above, we considered problems with the homogeneous initial conditions. In the
case of the inhomogeneous initial conditions, solutions to all these problems cease to
possess the property of spatial homogeneity, and equations assume very cumbersome
forms. However, similar to the case of the density field, the obtained solutions give
certain data in this case, too. For example, for the average energy of magnetic field in
the case of inhomogeneous initial conditions under the neglect of dynamic diffusion,
we obtain the expression (11.72), page 294,
Z
dr
h
E(r, t)
i
0
=
Z
dr E
0
(r) exp
2
d − 1
d
D
s
+ D
p
t
.

Passive Tracer Clustering and Diffusion 319
Problems
Problem 11.1
Derive the Fokker–Planck equation for particle position in random nondivergent
velocity field with allowance for the two-dimensional plane-parallel average flow
u
0
(r, t) = v(y)l, where r = (x, y), l = (1, 0).
Instruction Particle motion is described by the stochastic system of equations
d
dt
x(t) = v(y) + u
1
(r, t),
d
dt
y(t) = u
2
(r, t).
Solution
∂
∂t
+ v(y)
∂
∂x
P(t;r) = D
0
1P(t;r). (11.122)
Problem 11.2
Show that Eq. (11.122) is statistically equivalent to a particle whose dynamics is
described by the equations
d
dt
x(t) = v(y) + u
1
(t),
d
dt
y(t) = u
2
(t), (11.123)
where u
i
(t), i = 1, 2 are the statistically independent Gaussian delta-correlated
processes with the characteristics
h
u(t)
i
= 0,
u
i
(t)u
j
(t
0
)
= 2δ
ij
D
0
δ(t − t
0
).
Problem 11.3
Integrate Eqs. (11.123) and evaluate statistical characteristics of particle posi-
tion in the case of linear shear v(y) = αy.
Solution
y(t) = y
0
+ w
2
(t), x(t) = x
0
+ w
1
(t) +
t
Z
0
dτ v
(
y + w
2
(τ )
)
, (11.124)

320 Lectures on Dynamics of Stochastic Systems
where w
i
(t) =
R
t
0
dτ u
i
(
τ
)
are independent Wiener processes with the characte-
ristics
h
w(t)
i
= 0,
w
i
(t)w
j
(t
0
)
= 2D
0
δ
ij
min{t, t
0
}.
In all cases, coordinate y(t) has the Gaussian probability density with the
parameters
h
y(t)
i
= y
0
,
D
y
2
(t)
E
= y
2
0
+ 2D
0
t.
For the linear shear, Eqs. (11.124) correspond to the joint Gaussian probability
density with the parameters
h
y(t)
i
= y
0
,
h
x(t)
i
= x
0
+ αy
0
t,
σ
2
xx
(t) =
D
(
x(t) −
h
x(t)
i
)
2
E
= 2D
0
t
1 + αt +
1
3
α
2
t
2
,
σ
2
yy
(t) =
D
(
y(t) −
h
y(t)
i
)
2
E
= 2D
0
t,
σ
2
xy
(t) =
h
(
x(t) −
h
x(t)
i
) (
y(t) −
h
y(t)
i
)
i
= 2D
0
t
(
1 + αt
)
.
Problem 11.4
Derive the equation for the joint Eulerian probability density of the density
and density gradient fields in random Gaussian divergent, homogeneous, and
isotropic in space and delta-correlated in time velocity field.
Solution Averaging the Liouville equation (3.24), page 75, over an ensemble of
realizations of the velocity field, we obtain the equation of the form
∂
∂t
P(r, t;ρ, p) =
D
0
1 +
2
d
D
p
∂
2
∂r∂p
ρ + D
p
∂
2
∂ρ
2
ρ
2
+
1
d(d + 2)
D
s
b
L
s
( p)
+
1
d(d + 2)
D
p
b
L
p
( p) +
2(d + 1)
d
D
p
∂
∂p
p
∂
∂ρ
ρ +D
p
4
∂
2
∂p
2
ρ
2
P(r, t;ρ, p),
(11.125)
where operators
b
L
s
( p) and
b
L
p
( p) are defined by the formulas
b
L
s
( p) = (d + 1)
∂
2
∂p
2
p
2
− 2
∂
∂p
p − 2
∂
∂p
p
2
= (d + 1)
∂
2
∂p
2
p
2
− 2
∂
2
∂p
k
∂p
l
p
k
p
l
,
b
L
p
( p) =
∂
2
∂p
2
p
2
+ (d
2
+ 4d + 6)
∂
∂p
p
2
+ (d
2
+ 2d + 2)
∂
∂p
p

Passive Tracer Clustering and Diffusion 321
and diffusion coefficients D
0
, D
p
, and D
s
are given by Eqs. (4.54) and (4.59),
pages 107 and 108.
For the nondivergent velocity field (D
p
= 0) Eq. (11.125) becomes simpler
and assumes the form
∂
∂t
− D
0
1
P(r, t;ρ, p) =
1
d(d + 2)
D
s
b
L
s
( p)P(r, t;ρ, p). (11.126)
Problem 11.5
Derive the Fokker–Planck equation for the gradient of particle concentration in
nondivergent random velocity field in the case of the two-dimensional average
linear shear u
0
(r, t) = αyl, where r = (x, y), l = (1, 0).
Instruction In the Lagrangian description, the particle concentration gradient in
nondivergent velocity field satisfies the equations
d
dt
p
x
(t|r
0
) = −p
k
(
t|r
0
)
∂u
k
(r, t)
∂x
,
d
dt
p
y
(t|r
0
) = −αp
x
(t|r
0
) − p
k
(
t|r
0
)
∂u
k
(r, t)
∂y
,
p(0|r
0
) = p
0
(r
0
) = ∇ρ
0
(r
0
).
Solution
∂
∂t
P( p, t|r
0
) =
αp
x
∂
∂p
y
+
1
8
D
s
3
∂
2
∂p
2
p
2
− 2
∂
2
∂p
k
∂p
l
p
k
p
l
P( p, t|r
0
),
P( p, 0|r
0
) = δ
p − p
0
(r
0
)
. (11.127)
Problem 11.6
Starting from Eq. (11.127), study the behavior of statistical characteristics of
particle concentration gradient in nondivergent velocity field in the case of the
two-dimensional average linear shear u
0
(r, t) =αyl, where r=(x, y), l =(1, 0).
Solution Average gradient of tracer concentration field coincides with the prob-
lem solution for absent fluctuations of the velocity field
h
p
x
(t)
i
= p
x
(0),
p
y
(t)
= p
y
(0) − αp
x
(0)t.

322 Lectures on Dynamics of Stochastic Systems
The second moments of the gradient satisfy a closed system of equations with
the cubic characteristic equation in parameter λ
λ +
1
2
D
s
2
λ − D
s
=
3
2
α
2
D
s
whose roots essentially depend on parameter α/D
s
. For α/D
s
1, the approxi-
mate expressions for the roots are as follows
λ
1
= D
s
+
2α
2
3D
s
, λ
2
= −
1
2
D
s
+ i|α|, λ
3
= −
1
2
D
s
− i|α|.
Consequently, random factor completely determines the problem solution for
times D
s
t 2. This means that the effects of velocity field fluctuations pre-
dominate the effects of the weak gradient of linear shear. In the opposite limit
α/D
s
1, the approximate expressions for the roots have the form
λ
1
=
3
2
α
2
D
s
1/3
, λ
2
=
3
2
α
2
D
s
1/3
e
i(2/3)π
,
λ
2
=
3
2
α
2
D
s
1/3
e
−i(2/3)π
.
Because real parts of λ
2
and λ
3
are negative, the asymptotic solution of the sys-
tem for second moments for
3
2
α
2
D
s
1/3
t 1 has the form
D
p
2
(t)
E
∼ exp
(
3
2
α
2
D
s
1/3
t
)
,
from which follows that even small fluctuations of velocity field appear the gov-
erning factor in the case of shears characterized by strong gradients.
Problem 11.7
Derive the equation for the joint Eulerian probability density of the concen-
tration and concentration gradient fields in random nondivergent velocity field

Passive Tracer Clustering and Diffusion 323
in the case of the two-dimensional average linear shear u
0
(r, t) = αyl, where
r = (x, y), l = (1, 0).
Solution
∂
∂t
P(r, t;ρ, p) =
−αy
∂
∂x
+ D
0
1
P(r, t;ρ, p)
+
αp
x
∂
∂p
y
+
1
8
D
s
3
∂
2
∂p
2
p
2
− 2
∂
2
∂p
k
∂p
l
p
k
p
l
P(r, t;ρ, p).
The solution to this equation can be represented in the form of integral (11.58),
page 289, where Lagrangian probability densities P(r, t|r
0
) and P( p, t|r
0
) satisfy
Eqs. (11.123) and (11.127).
This page intentionally left blank

Lecture 12
Wave Localization in
Randomly Layered Media
12.1 General Remarks
The problem of plane wave propagation in layered media is formulated in terms of the
one-dimensional boundary-value problem. It attracts the attention of many researchers
because it is much simpler in comparison with the corresponding two- and three-
dimensional problems and provides a deeper insight into wave propagation in random
media. In view of the fact that the one-dimensional problem allows an exact asymp-
totic solution, we can use it to trace the effect of different models, medium parameters,
and boundary conditions on statistical characteristics of the wavefield.
The problem in the one-dimensional statement was given in Lecture 1.
12.1.1 Wave Incidence on an Inhomogeneous Layer
Assume the layer of inhomogeneous medium occupies the portion of space
L
0
< x < L. The unit-amplitude plane wave is incident on this layer from region
x > L. The wavefield in the inhomogeneous layer satisfies the Helmholtz equation
d
2
dx
2
u(x) + k
2
(x)u(x) = 0, (12.1)
where k
2
(x) = k
2
[1 + ε(x)] and function ε(x) describes the inhomogeneities of the
medium. In the simplest case of unmatched boundary, we assume that k(x) = k, i.e.,
ε(x) = 0 outside the layer and ε(x) = ε
1
(x) + iγ inside the layer, where ε
1
(x) is the
real part responsible for wave scattering in the medium and γ 1 is the imaginary
part responsible for wave absorption in the medium.
The boundary conditions for Eq. (12.1) are formulated as the continuity of function
u(x) and derivative
d
dx
u(x) at layer boundaries; these conditions can we written in the
form
1 +
i
k
d
dx
u(x)
x=L
= 2,
1 −
i
k
d
dx
u(x)
x=L
0
= 0. (12.2)
Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00012-X
Copyright
c
2011 Elsevier Inc. All rights reserved.
